Investigation of the Temperature Dependence of the Oscillation of the Magnetic Susceptibility in Semiconductors ()
1. Introduction
In a strong magnetic field, the energy spectrum of electrons in a semiconductor becomes quantized, so that the density of states as a function of energy acquires an oscillating character. This circumstance is the root cause of occurrence of oscillatory magnetic field dependence of a number of equilibrium and nonequilibrium quantities characterizing the state and behavior of the electrons in the crystal in a quantizing magnetic field. Currently, these oscillations are united under the general name of quantum oscillation effects [1] .
Effect de Haas-van Alphen (dHvA) is a versatile and powerful tool to study the energy spectrum of the free electron systems in semiconductors. The first time the definition of the oscillations of the magnetic susceptibility was observed experimentally in bismuth crystals at low temperatures and strong magnetic fields [2] .
dHvA effect in recent years due to intensive research of low-dimensional structures, primarily of semiconductor nanostructures in which the spectrum of the Landau levels is determined primarily positions dimensional quantization levels. [3] [4] detected dHvA oscillations at high temperatures and weak magnetic fields using measurements of the field and temperature dependences of the static magnetic susceptibility of nanoscale semiconductors.
Work [5] - [12] considered that the temperature dependence of the density of states is determined by relaxation spectroscopy of the energy levels in semiconductors. It has been shown that the density of surface states is temperature-dependent―a method of determining the density of surface states. It has been shown that due to the energy levels of thermal broadening, a discrete spectrum with a rise in temperature is transformed into a continuous energy spectrum. With the expansion of the energy spectrum of the density of states function GN has been shown that the value of the energy gap will depend on the temperature. These studies do not consider the properties of the magnetic oscillation effects in semiconductors.
The aim of this work is to study the temperature dependence of the magnetic susceptibility and the comparison of theoretical calculations with experimental results.
2. Influence of Temperature on the Magnetic Susceptibility in Semiconductors
Consider the free energy of the electron gas. According, the Gibbs distribution can be written as [13] [14]
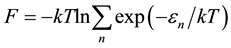 (1)
(1)
where,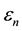 ―energy levels of the system.
―energy levels of the system.
The free energy F is expressed in terms of electron density of states Ns. The free energy of an electron in a quantizing magnetic field is determined by the following formula [15] :
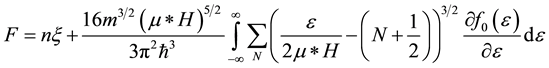 (2)
(2)
where,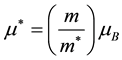 ―“effective” Bohr magneton,
―“effective” Bohr magneton,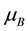 ―Bohr magneton, H―magnetic field strength, N― number of Landau levels,
―Bohr magneton, H―magnetic field strength, N― number of Landau levels,
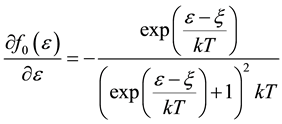 (3)
(3)
Second-order derivative of  in the magnetic field strength, the magnetic susceptibility has
in the magnetic field strength, the magnetic susceptibility has
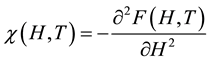 (4)
(4)
The occurrence of oscillations of the magnetic susceptibility 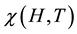 can be explained qualitatively as follows.
can be explained qualitatively as follows.
Figure 1 shows graphs of the oscillations of the magnetic susceptibility calculated by Formulas (2)-(4) in a
strong magnetic field at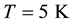 ,
,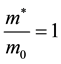 . At such low temperatures, the influence of the thermal broadening
. At such low temperatures, the influence of the thermal broadening
of the weak. Figure 1 shows that with increasing magnetic field strength, the oscillation amplitude of the magnetic susceptibility 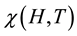 increases.
increases.
Figure 2 shows the oscillations of the magnetic susceptibility for different temperatures. As can be seen from these figures, at a temperature of 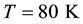 peaks effect dHvA oscillations due to Landau quantization is do not observed.
peaks effect dHvA oscillations due to Landau quantization is do not observed.
In work [10] to determine the probability devastation energy states showed that, if 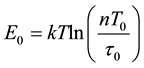 the
the
![]()
Figure 1. Dependence of the oscillation of the magnetic susceptibility of the strength magnetic field.
![]()
Figure 2. Change in the magnetic susceptibility at different temperatures in strong magnetic fields, calculated by Formulas (3) and (4).
function of probability devastation energy states is ![]() a step function, its derivative
a step function, its derivative
![]() (5)
(5)
at low temperatures describes―the Dirac delta function.
Function of the form ![]() satisfies all the conditions necessary to obtain the delta- function [15] :
satisfies all the conditions necessary to obtain the delta- function [15] :
![]()
From here follow, the function, ![]() , at
, at ![]() and
and ![]()
![]()
is a delta-Dirac function. It is well known that the derivative of the energy function is the Fermi-Dirac Dirac ![]() - function, tends to zero temperature.
- function, tends to zero temperature.
Thus, to study the temperature dependence of the magnetic susceptibility of the oscillations in the Formula (2) ![]() is replaced by the
is replaced by the ![]() -function.
-function.
Then we can calculate the temperature dependence of magnetic susceptibility of the oscillation with the aid of Formulas (2), (4) and (5).
3. Comparison of Theoretical Calculations with Experimental Results
In the work [2] experiments were conducted on bismuth in stronger magnetic fields and low temperatures. Initial data for the application of formulas (4) and (5) is an experimental oscillation of magnetic susceptibility at a particular temperature T (temperature experiment). Figure 3(a) shows the oscillation of the magnetic susceptibility at![]() . For analysis of the experimental results beginning requires expansion of the magnetic susceptibility in a series of
. For analysis of the experimental results beginning requires expansion of the magnetic susceptibility in a series of ![]() functions. On Figure 3(b) shows the theoretical fitting oscillation of the magnetic susceptibility obtained by the decomposition of the experimental schedule Figure 3(a) in a series of
functions. On Figure 3(b) shows the theoretical fitting oscillation of the magnetic susceptibility obtained by the decomposition of the experimental schedule Figure 3(a) in a series of ![]() functions. Comparing Figure 3(a) and Figure 3(b) shows that the oscillations of the magnetic
functions. Comparing Figure 3(a) and Figure 3(b) shows that the oscillations of the magnetic
![]() (a)
(a)![]() (b)
(b)
Figure 3. Changing the oscillations of magnetic susceptibility in a strong quan- tizing magnetic field. (a) Experiment [2] and the model calculation for bismuth at![]() ; (b) Oscillations of magnetic susceptibility in a strong magnetic field for three different values of temperature.
; (b) Oscillations of magnetic susceptibility in a strong magnetic field for three different values of temperature.
susceptibility of bismuth observed at the temperature of the experiment. Because, in this experiment
![]() , at temperature
, at temperature![]() .
.![]() ,
,![]() . In this case, the Landau levels appear ab-
. In this case, the Landau levels appear ab-
ruptly. With increasing temperature starts to smooth sharp spikes and at sufficiently high temperatures![]() ,
, ![]() turns into a continuous spectrum of the magnetic susceptibility. Figure 3(b) shows
turns into a continuous spectrum of the magnetic susceptibility. Figure 3(b) shows ![]() for different temperatures in a strong magnetic field. At a temperature of 100 K for bismuth oscillations of magnetic susceptibility is do not observed. Theoretical calculations for these materials are in good agreement with the experimental data.
for different temperatures in a strong magnetic field. At a temperature of 100 K for bismuth oscillations of magnetic susceptibility is do not observed. Theoretical calculations for these materials are in good agreement with the experimental data.
4. Conclusion
The dependence of the oscillation of the magnetic susceptibility of the temperature in a quantizing magnetic field by the free energy of the electrons was investigated. It is shown that, as temperature is increased starts to smooth sharp spikes and at sufficiently high temperatures ![]() turns into a continuous spectrum of oscillations of the magnetic susceptibility. Mathematical simulation of the processes with the use of experimental results for bismuth [2] at low temperatures and strong magnetic field
turns into a continuous spectrum of oscillations of the magnetic susceptibility. Mathematical simulation of the processes with the use of experimental results for bismuth [2] at low temperatures and strong magnetic field![]() , the calculated high-temperature oscillation dHvA effect. Simulation of the temperature dependence of the oscillation allowed determined magnetic susceptibility of bismuth in wide temperature ranges.
, the calculated high-temperature oscillation dHvA effect. Simulation of the temperature dependence of the oscillation allowed determined magnetic susceptibility of bismuth in wide temperature ranges.