1. Introduction
“We make our world significant, by the courage of our questions and, by the depth of our answers.”
Carl Sagan (1934-1996).
Despite the dearth of solid experimental proof [cf.] [1] - [5] , it is generally agreed (perhaps believed) that photons have no mass. Though this notion of a zero-mass photon has been questioned over the years [cf.] [6] -[8] , this deeply entrenched fact has been deduced from two (seemingly) immutable facts of experience so well supported by experimental evidence. The first is Professor Albert Einstein [9] ’s energy-momentum dispersion relation, namely:
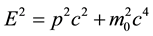 (1)
(1)
where  is the total energy of the particle,
is the total energy of the particle, 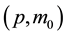 are the particle’s momentum and rest mass respectively while
are the particle’s momentum and rest mass respectively while 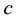 is the speed of light in vacuum The second fact is that the energy of the photon has been found from experience to be given by:
is the speed of light in vacuum The second fact is that the energy of the photon has been found from experience to be given by:
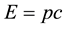 (2)
(2)
If (1) and (2) are both applicable to the photon with all the identical symbols holding the same meaning, then, it follows directly that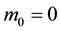 ; that is, the rest mass of the photon must be zero. This is generalised and stated in a figure of speech by physicists by saying “the photon has no mass”. It is thus accepted that if a particle has zero rest mass, it will travel at the speed of light cf, [10] . Conversely, if a particle travels at the speed of light, its rest mass must vanish identically. Therein the reading [11] , the two dispersion relations (1) and (2) are placed in the dock for some cross-examination, where-after an interesting conclusion is reached namely that it must in-prin- ciple be possible to have massive photons (i.e. non-zero rest mass photons) obeying these two relations simul- taneously and concurrently i.e., massive particles that travel at the speed of light
; that is, the rest mass of the photon must be zero. This is generalised and stated in a figure of speech by physicists by saying “the photon has no mass”. It is thus accepted that if a particle has zero rest mass, it will travel at the speed of light cf, [10] . Conversely, if a particle travels at the speed of light, its rest mass must vanish identically. Therein the reading [11] , the two dispersion relations (1) and (2) are placed in the dock for some cross-examination, where-after an interesting conclusion is reached namely that it must in-prin- ciple be possible to have massive photons (i.e. non-zero rest mass photons) obeying these two relations simul- taneously and concurrently i.e., massive particles that travel at the speed of light .
.
The hidden assumption in all the reasoning leading to the fact that for photons , is that the energies
, is that the energies  in the formulae
in the formulae 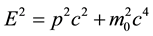 and
and  are identical. On a more fundamental level, there is no priori nor posteriori justification for this clandestine assumption. If these two energies are different, that is, say the
are identical. On a more fundamental level, there is no priori nor posteriori justification for this clandestine assumption. If these two energies are different, that is, say the 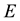 in
in 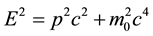 is the total gravitational energy
is the total gravitational energy 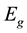 of the photon so that
of the photon so that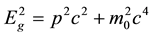 ; and the
; and the 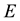 in
in ![]() is say total kinetic energy
is say total kinetic energy ![]() of the photon so that
of the photon so that![]() , then, it is possible for
, then, it is possible for![]() . Combining these (i.e.,
. Combining these (i.e., ![]() and
and![]() ) would lead to
) would lead to ![]() where generally
where generally![]() . In the same reading [11] , a more powerful argument has been presented, where it is argued that the photon mass may be very small, leading to its non-detection. Herein, we present an even more powerful argument where we argue that the photon mass should not submit to direct detection by means presently being used to try and measure it.
. In the same reading [11] , a more powerful argument has been presented, where it is argued that the photon mass may be very small, leading to its non-detection. Herein, we present an even more powerful argument where we argue that the photon mass should not submit to direct detection by means presently being used to try and measure it.
The idea of a zero-mass particle usually presents a challenge to freshman students encountering this for the first time [12] because, mass is generally thought to be the measure of the amount of matter in a substance. Based on this kind of thinking, zero-mass must mean no amount of matter present yet for the photon whose mass is zero, it has not only stuff in it, but lots of it. Can a massive photon solve this problem?
In the present reading, first we show that the idea founded in the reading [13] that the four vector potential (and most certainly all physical observables) must be ![]() matrices, this idea enables us to obtain a massive gauge invariant theory of Proca Electrodynamics (PED) at the classical level. In the second instance, we forego the traditional Lorenz gauge condition
matrices, this idea enables us to obtain a massive gauge invariant theory of Proca Electrodynamics (PED) at the classical level. In the second instance, we forego the traditional Lorenz gauge condition![]() , and in so going, demonstrate that one can get rid of the mass term of PED without having to set it equal to zero. The resulting theory is a theory of massive photons that are seen able to take part in long range interactions without any problem whatsoever.
, and in so going, demonstrate that one can get rid of the mass term of PED without having to set it equal to zero. The resulting theory is a theory of massive photons that are seen able to take part in long range interactions without any problem whatsoever.
The remainder of this reading is organised as follows. In Section 2, we give an exposition of PED and thereafter in Section 3, we give the theory or set of ideas leading to a gauge invariant theory of massive long range photons. With respect to experimental and observational philosophy, in Section 4, we discuss the meaning of the new theory and thereafter in Section 5, we give a general discussion and the conclusion drawn thereof.
2. Proca Electrodynamics
As is well known, Maxwellian Electrodynamics (MED) is based on the hypothesis of a massless photon. If at all, what evidence there is for this, experience is yet to furnish us with a solid answer. As regards the quintessence of a zero-mass photon is the resulting gauge invariance of MED i.e., to those that seek beauty in a physical theory, one appealing feature of MED is that it quantum mechanical version i.e. Quantum Electrodynamics (QED) is constructed from a gauge invariant Lagrangian. Gauge invariance was first introduced by Professor Herman Weyl [14] ; it plays a central role not only in field theory but in physics as a whole. However, if one abandons this, they can―as the great Romanian physicist Professor Alexandru Proca (1897-1955) did; construct an electrodynamic theory were the photon has a non-zero mass via the Proca Lagrangian![]() , that is:
, that is:
![]() (3)
(3)
where ![]() is the dimensionless electrodynamic four vector potential,
is the dimensionless electrodynamic four vector potential, ![]() is the four electrodynamic current,
is the four electrodynamic current, ![]() is the permeability of free space,
is the permeability of free space, ![]() is mass term of the photon and:
is mass term of the photon and:
![]() (4)
(4)
is the electromagnetic field tensor. As usual, the Greek indices ![]() run from 0 to 3, i.e.
run from 0 to 3, i.e.![]() .
.
The term ![]() is the classical Maxwellian Electrodynamic Lagrangian. The factor
is the classical Maxwellian Electrodynamic Lagrangian. The factor ![]() in the Proca mass term is usually given as
in the Proca mass term is usually given as ![]() in most if not all readings where PED is discussed. Here, we have chosen to make this factor
in most if not all readings where PED is discussed. Here, we have chosen to make this factor ![]() and this has been done so that when we come to (21) we can obtain the ex-
and this has been done so that when we come to (21) we can obtain the ex-
pected normalization condition for the four vector![]() , that is
, that is![]() .
.
The equations of motion associated with the Proca Lagrangian ![]() are obtained from the usual Lagrangian Equation of motion, namely:
are obtained from the usual Lagrangian Equation of motion, namely:
![]() (5)
(5)
and the resulting Equation is:
![]() (6)
(6)
Since![]() , the above Proca-Maxwell Equation can be rewritten as:
, the above Proca-Maxwell Equation can be rewritten as:
![]() (7)
(7)
The over-brace has been inserted in the above Equation and this has been done for latter purposes so as to make it easy to reference.
Now, if we are to institute the Lorentz gauge condition![]() , the above Equation can further be written as:
, the above Equation can further be written as:
![]() (8)
(8)
where:
![]() (9)
(9)
is the usual D’Alembert operator.
To see why is is said that mass photons must lead to only short range interaction we have to solve (8) and, for simplicity, we shall assume that spatially, ![]() only has a radial dependence. In the static limit (8) truncates to:
only has a radial dependence. In the static limit (8) truncates to:
![]() (10)
(10)
and in empty space, the electric potential ![]() is given by the Yukawa potential:
is given by the Yukawa potential:
![]() (11)
(11)
where ![]() is the permittivity of free space. As is well known, this potential can only explain short and not long range forces such as the electromagnetic force. To explain the long range interaction, we must have
is the permittivity of free space. As is well known, this potential can only explain short and not long range forces such as the electromagnetic force. To explain the long range interaction, we must have![]() , that is, the mass of the photon with mediate the electromagnetic force, must vanish identically. This is one of the strongest reasons (if not the sole reason) for assuming that the photon mass must be zero since the electromagnetic interaction is a long range phenomenon.
, that is, the mass of the photon with mediate the electromagnetic force, must vanish identically. This is one of the strongest reasons (if not the sole reason) for assuming that the photon mass must be zero since the electromagnetic interaction is a long range phenomenon.
For a minute, let us pause a question. What if we can show that within the framework of the same theory just laid down above (i.e. PED), that, one can obtain the desired long range Coulomb potential for a non-vanishing photon mass? Would the above reason for assuming a non-zero photon mass still hold? We think not. This is what we shall do in the next section; we shall present a trivially simple condition for attaining the said.
3. Theory
In the present section, we will address the two issues that make a massive photon non-desirable and these are the issue of gauge invariance and the issue that these massive photons can only be short range. In Section 3.1, we show that if the components of the four potential ![]() where to be a
where to be a ![]() matrix, it is possible to overcome the gauge invariance problem associated with massive photons. In Section 3.2, we show that if one where to appropriately modify the Lorenz gauge condition
matrix, it is possible to overcome the gauge invariance problem associated with massive photons. In Section 3.2, we show that if one where to appropriately modify the Lorenz gauge condition![]() , they can obtain a theory in which massive photons take part in long range interactions.
, they can obtain a theory in which massive photons take part in long range interactions.
3.1. Massive Gauge Invariant Photons
If the following anti-commutator relations are to hold true, i.e.:
![]() (12)
(12)
then, it is crystal clear that the following gauge transformations:
![]() (13)
(13)
will leave the Maxwell-Proca Lagrangian (3) completely invariant. The anti-commutator relations (12) will require that![]() ,
, ![]() and
and ![]() must be matrices and not zero-rank objects. The idea of
must be matrices and not zero-rank objects. The idea of ![]() and
and ![]() being
being ![]() matrices has been advanced in the reading [13] where a Unified Field Theory (UFT) of all the forces of Nature i.e., the gravitational, electromagnetic, the weak and the strong nuclear force has been advanced. We will not try to justify this idea here, instead, we will refer the reader to the reading [13] , where they can convince themselves that indeed, this idea of observables being represented by
matrices has been advanced in the reading [13] where a Unified Field Theory (UFT) of all the forces of Nature i.e., the gravitational, electromagnetic, the weak and the strong nuclear force has been advanced. We will not try to justify this idea here, instead, we will refer the reader to the reading [13] , where they can convince themselves that indeed, this idea of observables being represented by ![]() matrices does make a lot of sense as it leads us naturally for the simplest imaginable UFT of all the forces of Nature.
matrices does make a lot of sense as it leads us naturally for the simplest imaginable UFT of all the forces of Nature.
If the reader accepts the idea that![]() ,
, ![]() and
and ![]() can be represented as
can be represented as ![]() matrices, then it is clear that if we set:
matrices, then it is clear that if we set:
![]() (14)
(14)
where![]() ,
, ![]() and
and ![]() are zero-rank objects, where:
are zero-rank objects, where:
![]() (15)
(15)
then, the relations (12) will be possible, thus, leading to the gauge transformations (13) to leave the Maxwell-Proca Lagrangian (3) completely invariant as desired. In this way, we solve once and for altime this nagging problem of obtaining a gauge invariant Maxwell-Procca Lagrangian. This comes at the cost of:
1) Making the current![]() , the four potential
, the four potential ![]() and the gauge function
and the gauge function![]() , entities whose components are
, entities whose components are ![]() matrices.
matrices.
2) Making the current ![]() to transform under a gauge transformation.
to transform under a gauge transformation.
Before we close this section, we need to say something about![]() . If one where to apply the gauge transformations (13) to (8), they would undoubtedly come to the conclusion that:
. If one where to apply the gauge transformations (13) to (8), they would undoubtedly come to the conclusion that:
![]() (16)
(16)
In massless MED, the function ![]() satisfies the massless Klein-Gordon Equation
satisfies the massless Klein-Gordon Equation![]() . Here in the massive non-Lorenz gauge invariant PED,
. Here in the massive non-Lorenz gauge invariant PED, ![]() satisfies the massive Klein-Gordon Equation (16).
satisfies the massive Klein-Gordon Equation (16).
3.2. Massive Long Range Photons
The reasons why the photon is considered massless have been discussed in the previous sections. Of particular concern here is the fact that because the electromagnetic interaction is a long range interaction, therefore, the intermediate vector Boson―the photon; must be massless for this to be so. If we can demonstrate that even a massive photon can mediate long range interactions, will the above reason for vanishing photon mass still hold? We think not.
Notice that if we set equal to zero the over-braced terms in (7), then, we would obtain the same Equations that are obtained in the case of a Lorenz gauge invariant massless photon i.e. Equation (10) with ![]() on the constraint
on the constraint![]() . To have these terms under the over-brace set equal to zero i.e.:
. To have these terms under the over-brace set equal to zero i.e.:
![]() (17)
(17)
requires that we abandon the Lorenz gauge i.e. set![]() , where
, where![]() . The condition (17) is now the
. The condition (17) is now the
new gauge condition that replaced the Lorenz gauge condition![]() .
.
Since![]() , it follows that (17) can be rewritten as:
, it follows that (17) can be rewritten as:
![]() (18)
(18)
so that:
![]() (19)
(19)
where ![]() is a fundamental natural constant that does not vary with space nor time or any physical variable for that matter. In this way, we obtain a massive long range photon theory. This comes at the expense of doing away with the Lorenz gauge. In the reading [3] , the new Lorenz gauge condition
is a fundamental natural constant that does not vary with space nor time or any physical variable for that matter. In this way, we obtain a massive long range photon theory. This comes at the expense of doing away with the Lorenz gauge. In the reading [3] , the new Lorenz gauge condition ![]() emerges naturally and is not imposed.
emerges naturally and is not imposed.
With the over-brace terms set to zero, (7) reduces to:
![]() (20)
(20)
Equation (20) is the same Equation obtained in the case of massless photon under the Lorenz gauge. We know that Equation (20) leads to long range and long lived photon. The difference now is that, these photons are now massive instead of massless.
Now, in-order that electric charge and current are conserved ![]() as is the case is the real world, it follows from (20) we must have
as is the case is the real world, it follows from (20) we must have![]() . If
. If![]() , then according to (18), we must have:
, then according to (18), we must have:
![]() (21)
(21)
Therefore, the condition![]() , is a different expression of the relation
, is a different expression of the relation![]() , which is merely a normalisation condition for the four vector
, which is merely a normalisation condition for the four vector![]() , hence it is possible to have a gauge invariant massive long range photon theory as proposed herein since the theory contains no internal inconsistencies or hiccups.
, hence it is possible to have a gauge invariant massive long range photon theory as proposed herein since the theory contains no internal inconsistencies or hiccups.
3.3. Massive Long Lived Photons
Under the usual or the traditional Proca Electrodynamics, a massive photon is expected to decay on a time scale ![]() cf, [15] . Since photons created during the supposed moment of creation in the so-called Big Bang Theory (BBT)―a theory that is largely believed to give an accurate account of the origins, evolution and fate of Universe; the age of the Universe is thought to be about
cf, [15] . Since photons created during the supposed moment of creation in the so-called Big Bang Theory (BBT)―a theory that is largely believed to give an accurate account of the origins, evolution and fate of Universe; the age of the Universe is thought to be about ![]() [16] . From this and given the relation
[16] . From this and given the relation![]() , it would mean
, it would mean![]() . Under the proposed modifications to Proca Electrodynamics via the new gauge condition (17 or 18), massive photons will be stable, living forever, from antiquity to eternity. This same gauge condition (17 or 18) is what guarantees massive photons to be long ranged, that is, to travel an infinite distance without diminishing their power.
. Under the proposed modifications to Proca Electrodynamics via the new gauge condition (17 or 18), massive photons will be stable, living forever, from antiquity to eternity. This same gauge condition (17 or 18) is what guarantees massive photons to be long ranged, that is, to travel an infinite distance without diminishing their power.
4. Measurements of Photon Mass
Tu et al. [7] ’s excellent review article diligently touches on the many efforts that have been conducted to measure the mass of the photon. These efforts can be classified into two categories:
1) Laboratory Experiments e.g., [17] [18] .
2) Large Scale Observations e.g., [5] [19] -[22] .
In these measurements, derivations from MED are sought because the addition of the Proca term invariably modifies two of Maxwell’s four Equations i.e., the source coupled field Equations. These two Equations are:
![]() (22)
(22)
where ![]() and
and ![]() are the electric field at the position vector
are the electric field at the position vector ![]() and the charge density enclosed in the sphere of radius
and the charge density enclosed in the sphere of radius ![]() respectively. The second Equation is:
respectively. The second Equation is:
![]() (23)
(23)
where![]() ,
, ![]() and
and ![]() are the magnetic field, the magnetic vector potential, and the current density, respectively. In these Equations (i.e. 22 and 23),
are the magnetic field, the magnetic vector potential, and the current density, respectively. In these Equations (i.e. 22 and 23), ![]() and
and ![]() are pure constants―this is a central assumption of MED.
are pure constants―this is a central assumption of MED.
In the large scale observations, the deviations are sought from Solar and planetary magnetic fields while in laboratory experiments these deviations are sought from usual laboratory magnetic fields and electric circuits. In both the laboratory and large scale observational measurements, the mass of the photon is not measured directly but limits to the photon mass are derived. Laboratory measurements find upper limits in the range ![]() while large scale measurements find
while large scale measurements find ![]() [7] .
[7] .
Clearly, the equivalent of Equations (22) and (23) to be derived from (20) will contain no mass-term hence, it follows that if one where to try and use Equations (22) and (23) as happens in all effort to measure the mass of the photon, they must obtain values of the photon mass that are compatible with zero because the actual final Equations (20) under the proposed scheme, this term does not appear in Equations (22) and (23), implying that this term is identically equal to zero, hence a mass compatible with zero is expected to be detected if one where to assume Equations (22) and (23) for![]() . Thus, the present scheme or set of ideas―namely the gauge condition (18), conceals the mass-term in Equations (22) and (23).
. Thus, the present scheme or set of ideas―namely the gauge condition (18), conceals the mass-term in Equations (22) and (23).
5. General Discussion
Using the idea from the reading [13] where an attempt at all-encompassing UFT of all the known Forces of Nature has been given; the idea that physical observables and quantities are to be represented as ![]() hermitian matrices, we did show herein that if the components of the four potential
hermitian matrices, we did show herein that if the components of the four potential ![]() where to be expressed as
where to be expressed as ![]() hermitian matrices, then, one can obtain a gauge invariant theory of massive photons. Amongst other problems, massive photons do come along with a problem insofar as gauge invariance is concerned. Although this problem can successfully be solved using the Stückelberg mechanism [23] and other methods (e.g., Podolsky Electrodynamics cf. [24] ) which are usually descendants of the original Stückelberg mechanism, these methods usually introduce new scalar particles.
hermitian matrices, then, one can obtain a gauge invariant theory of massive photons. Amongst other problems, massive photons do come along with a problem insofar as gauge invariance is concerned. Although this problem can successfully be solved using the Stückelberg mechanism [23] and other methods (e.g., Podolsky Electrodynamics cf. [24] ) which are usually descendants of the original Stückelberg mechanism, these methods usually introduce new scalar particles.
In comparison to the Stückelberg mechanism and its descendants, the present method (theory) does not need the addition of a new assortment of particles to achieve gauge invariance. According to Occam’s Razor which requires a minimal addition of parameters into a theory, this fact that in the present theory we do not include nor need a menagerie of scalars as is the with the Stückelberg mechanism, this fact alone may be considered to be a significant improvement insofar a massive photon theory is concerned.
Another problem associated with massive photons is that such photons will have three extra degrees of freedom [7] [25] because apart from transverse degrees and there would come an extra set of degrees of freedom from longitudinal degree of freedom that comes about due to the fact that a mass photon is capable of the state
of rest. The total energy ![]() of a ‘normal’ massless photon at a temperature
of a ‘normal’ massless photon at a temperature ![]() is
is![]() . According
. According
to the equipartition theorem, adding three degrees of freedom will result in the photon gaining an extra amount
of energy ![]() namely
namely![]() , leading to its total energy being
, leading to its total energy being![]() . If one where to take this
. If one where to take this
into account in deriving Planck’s radiation law―then, in complete contradiction with results from experimental philosophy, this would alter the Planck’s radiation law by a factor of![]() . Such a paradigm shift would be measurable cf. [25] .
. Such a paradigm shift would be measurable cf. [25] .
The above stated problem associated with the massive photon comes about because the Proca photon is capable of being at rest. That is to say, there exists a Lorentz frame in which the photon is at rest and in the this rest frame, it has three degrees of freedom. This problem is solved by making the mass of the photon to be dependant on the photon’s frequency (wavelength). As shown in [11] , such a photon has no state of rest as the magni-
tude of its group velocity ![]() is such that
is such that![]() . Therefore, just as in the case of the massless photon,
. Therefore, just as in the case of the massless photon,
the present gauge invariant massive long range and long lived photon has three and not six degrees of freedom.
In-closing, allow us to say that in our most modest view, it is with great confidence that we have say that the present reading, together with [11] , may prove in the future prove to be significant contributions to physics. The reason for saying this is because we have shown from within the confines, provinces and domains of acceptable contemporary physics without the infusion of exogenous and exotic ideas that, in principle, it must be possible to have gauge invariant massive long range and long lived photons that travel at the speed of light. Given that massive photons long range and long lived have serious implications on the broad spectrum of physics at its most fundamental level, this reading may prove to be very useful and significant on the fundamental level. There is need to study the present findings much further than has been done herein because a massive photon has serious implications on the broad spectrum of physics.
6. Conclusions
Assuming the correctness (or acceptability) of the ideas presented herein, we hereby make the following conclusions:
1) It is in principle possible to have gauge invariant massive long lived photons that take part in long range interactions.
2) As suggested in [11] , the existence of massive photons may provide answers to the currently hot issue of the observed time delays in GRBs for photons of different frequencies. From these measured time delays in Gamma Ray Bursts (GRBs) for photons of different frequencies, the mass of photons may be measured using the ideas presented in [11] via the frequency dependence of the speed of light implied by a massive photon.
3) Due to the new gauge condition (18)’s concealment of the mass of the photon from the corridors of Maxwell’s Equations for a massive photon, experiments and observations based on the Proca Equations (22) and (23) are not expected to yield a mass of the photon that is compatible with zero because this term does not appear in the final Equation of a massive photon as presented herein. This non-appearance of the mass-terms implies that measurements which make use of Equations (22) and (23) for a massive photon must fail to detect a non-zero mass for the photon.
Acknowledgements
We are grateful to the National University of Science & Technology (NUST)’s Research & Innovation Department and Research Board for their unremitting support rendered toward our research endeavours; of particular mention, Prof. Dr. P. Mundy, Dr. P. Makoni and Prof. Y. S. Naik’s unwavering support. This reading is dedicated to my mother Setmore Nyambuya and to the memory of departed father Nicholas Nyambuya. (27.10.1947- 23.09.1999).