Ionization of Metastable 2P-State Hydrogen Atoms by Electron Impact for Coplanar Asymmetric Geometry

S. Dhar^*, N. Nahar

Department of Mathematics, Chittagong University of Engineering and Technology, Chittagong, Bangladesh.

DOI: 10.4236/ojm.2014.44007                

Abstract

The triple differential cross-sections of First Born approximation have been calculated for ionization of metastable 2P-state hydrogen atoms by electron impact in the asymmetric coplanar geometry. In this study a multiple scattering theory of ionization of hydrogen atoms is used. The latest results of the present method are compared with other calculations. It will be added for new experimental study of ionization of hydrogen atoms in their metastable states.

Keywords

Ionization, Scattering, Cross-Section, Electron

1. Introduction

Atomic ionization of atoms by charged particles like electron or positron forms an important class of Atomic Physics. Accurate determination of cross-section results of various types such as single, double and triple differential with varied kinematics conditions [1] -[12] offers very interesting and challenging problems to Applied Mathematics. With the availability of new experimental results over the last four decades a new dimension has been added in this field of research such as Astrophysics, Plasma Physics and Fusion research technology. It now appears that the investigation of ionization from metastable 2S-state [13] -[15] hydrogen atoms and ionization of medium heavy atoms [16] -[19] as well as linear superposition of 2S- and 2P-state [20] -[22] of hydrogen atoms by charged particles is equally interesting and the time is not far off when experimental results will be available in this field. Lewis integral [23] is used in the present calculation. At present, beyond the First Born results there exists the second Born calculations [12] [21] for small momentum transfer asymmetric scattering at the intermediate incident energies 150 eV, 250 eV and 400 eV. Here we presented a few new sets of theoretical results following the multiple scattering theory [1] [9] . It may be noted that using this multiple scattering theory [1] [9] gives good cross-section results for the electron-atom ionization both in the ground state [9] -[12] and in the metastable 2S state [13] -[15] and many other calculations, the references of which are not given here. The energy spectrum of scattered electrons in the K-shell ionization of medium-heavy atoms by fast electrons is nicely represented [16] -[19] by the use of scattering state wave function of Das and Seal [1] [9] multiplied by a suitable spinor. So the present First Born results for ionization from the 2P state may also be expected to be good, interesting and significant. The present calculation reveals new features in the cross-section curves which may be confirmed by experiments .The physical origin of the findings of the different features is presented here.

2. Theory

The most detailed information presently available about single ionization processes of the following type,

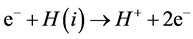(1)

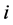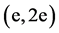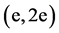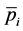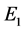where, the symbol denotes the initial state of the target, has been obtained in the coplanar geometry by analyzing triple differential cross sections (TDCS) measured in coincidence experiments. The TDCS is a measure of the probability that in an reaction an incident electron of momentum and energy will produce on collision with the target two electrons having energies and 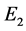and momenta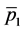, , emitted respectively into the solid angles and centered about the directions 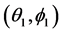and.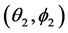

The TDCS is usually denoted by the symbol. For unpolarized incident electrons and targets, it is a function of the quantities, or, , and. By integrating the TDCS over, or one can form various double and single differential cross sections. We will calculate the same. Finally, the total ionization cross section is obtained by integrating over all outgoing scattering angles and energies, and depends only on, the incident electron energy.

It is useful when studying coincidence experiments to distinguish between several kinematical arrangements, since these have important implications for the theoretical analysis of the collision as we shall see later. A first distinction can be made between coplanar geometries-such that the momenta, and are in the same plane-and non-coplanar geometries such that the momentum is out of the reference plane.

The kinematics of an reaction. The incident electron momentum is and the momenta of the outgoing electrons are, respectively. Also shown are the angles and with respect to the incident direction and the angle measuring the direction in coplanar situation.

The multiple scattering theory of ionization of hydrogen atoms by electrons is described in detail [1] [11] [12] [14] . Here we will describe the method very briefly, for the particular case of hydrogenic 2P states at intermediate and high energies. The direct T-matrix element for ionization of hydrogen atoms by electrons, may be written as,

(2)

where, the perturbation potential is given by,

for hydrogen atom nuclear charge, and are the distances of the two electrons from the nucleus and is the distance between the two electrons.

Interaction between two electrons and nucleus.

The initial channel unperturbed wave function is,

(3)

where, is the hydrogenic wave function, is the incident electron momentum, and is the final three-particle scattering state with the electrons being in the continuum with momenta , . Co-ordinates of the two electrons are taken to be and . Here is approximated by a wave function is given by [1] ,

(4)

where,

, , ,

The normalization constant is given by,

(5)

where,

Here is the Coulomb wave function given by,

where,

for , for and for .

Now applying Equations (3) and (4) in Equation (2), we get

(6)

where,

(7)

(8)

(9)

(10)

For First Born approximation, we will calculate matrix amplitude of Equation (7) using [8] ,

After analytical calculation by using the Lewis integral [23] , we evaluated these expressions numerically us- ing Gaussian quadrature formula. The triple differential cross-section (TDCS) is finally given by

(11)

where is the energy of the incident electron. Therefore, in our present calculation we have computed the TDCS, given by Equation (11).

3. Results and Discussion

We have presented here First Born approximation Triple differential cross-section (TDCS) for the process (1) at intermediate incident energies and for some varied ejected angles and fixed scattering angles. The present results have been displayed in nine figures where we have plotted the electron impact TDCS by varying the angle of ejection of the ejected electron. In all figures, the region for and , refers to the recoil region, while and refers to the binary region. We con- sidered here to .

The present First Born approximation TDCS results in the metastable 2P-state hydrogen atoms are presented in the Figures 1(a)-(d), and Figures 2(a)-(e) for scattering in a plane. Here the incident electron energy is and scattering angles are and ejection

angle varies from to (measured oppositely from the forward direction compared to that for scattering angle ). We also computed TDCS for the same state for the incident energies and

and scattering angles are and , presented in Figure 1(b) and Figure1(d) respectively.

When we compared the present First Born results to the linear superposition of the 2S-state and 2P-state ionization [21] , it is noted that the TDCS exhibits a distinct four loaded structure where both the binary and recoil regions consist of two distinct peaks of comparable magnitudes as shown in Figures 1(a)-(d). In the present First Born TDCS (see Figures 1(a)-(d) and Figures 2(a)-(e)), for the metastable 2P-state ionization, exhibit two dis- tinct peaks both in the recoil and the binary, at all incident energies . The

(a) (b)(c) (d)

Figure 1. (a) The TDCS impact as a function of the ejected electron angle at , , . Solid curve: present First Born result, Dashed curve: result of Deb et al. [21] ; (b) The TDCS impact as a function of the ejected electron angle at , , . Solid curve: present First Born result, Dashed curve: result of Deb et al. [21] ; (c) The TDCS impact as a function of the ejected electron angle at , , . Solid curve: present First Born result, Dashed curve: result of Deb et al. [21] ; (d) The TDCS impact as a function of the ejected electron angle at , . Solid curve: present First Born result, Dashed curve: result of Deb et al. [21] .

binary peak arises due to the electron-electron interaction while the recoil peak is due to the projectile nucleus interaction.

The present First Born TDCS in the metastable 2P-state ionization for the incident energy and higher scattering angles shows dissimilar magnitude peaks in the recoil region (see Figures 2(a)-(e)). Hence these Figures 2(a)-(e) reveal that at the incident energy and the higher scattering angles the collision becomes almost recoil peaks less prominent in the metastable 2S-state [13] than the present metastable 2P-state calculation results. It may be expected. But here, in the binary region, the present peak values are slightly smaller than the corresponding compared 2S-state results of Dhar [13] .

The present binary peaks are shifted to the higher ejected scattering angles in the recoil region (see Figures 1(a)-(d)). But in the binary regions peaks are nearly similar pattern same with different magnitudes.

It is clear that the present First Born TDCS results almost agree with the linear combination of the 2S- and 2P- state results of Deb et al. [21] and the previous that of the metastable 2S-state results of Dhar [13] . But in some cases our results disagree in the recoil regions.

Amplitude corresponds to other three terms in the Equation (6) are also calculated and will be reported in near future.

The physical origins of finding cross-section results for 150 eV, 250 eV and 400 eV energies are presented. Here the amplitude (the First Born amplitude) corresponds to the first term on the right hand side of Equation (6) in which the scattered electrons of momentum are described by a plane wave while the ejected electrons of momentum are described by a coulomb wave. Also the physical origin of the peaks in the cross-section curves has been investigated, scattering first by atomic nucleus or atomic electron and then by atomic electron for the second time.

(a)(b) (c)(d) (e)

Figure 2. (a) The TDCS impact as a function of the ejected electron angle at , , . Solid curve: present First Born result, Dashed curve: 2S-state result [13] ; (b) The TDCS impact as a function of the ejected electron angle at, , . Solid curve: present First Born result, Dashed curve: 2S-state result [13] ; (c) The TDCS impact as a function of the ejected electron angle at , , . Solid curve: present First Born result, Dashed curve: 2S-state result [13] ; (d) The TDCS impact as a function of the ejected electron angle at , , . Solid curve: present First Born result, Dashed curve: 2S-state result [13] ; (e) The TDCS impact as a function of the ejected electron angle at, , . Solid curve: pre- sent First Born result, Dashed curve: 2S-state result [13] .

4. Conclusion

In the present study we have calculated triple differential cross sections (TDCS) for ionization of metastable 2P-state hydrogen atoms by 150 eV, 250 eV and 400 eV electron impact. It reveals additional possible features of the cross-section curves for small momentum transfer. Hence the present calculation provides significant contribution in the field of metastable 2P-state ionization problem. Thus, new experimental results will be more interesting and significant for metastable 2P-state hydrogen atoms by electrons scattering problems.

Acknowledgements

The computational works have been performed in the Simulation Lab of the Department of Mathematics, Chittagong University of Engineering and Technology.

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Das, J.N. (1990) Momentum-Space Analysis of Scattering States with Possible Application to Atomic Ionization. Physical Review A, 42, 1376. http://dx.doi.org/10.1103/PhysRevA.42.1376
[2]	Byron, Jr., F.W. and Joachain, C.J. (1989) Theory of (e, 2e) Reactions. Physics Reports, 179, 211-272. http://dx.doi.org/10.1016/0370-1573(89)90158-0
[3]	Ehrhardt, H., Jung, K., Knoth, G. and Schlemmer, P. (1986) Differential Cross Sections of Direct Single Electron Impact Ionization. Zeitschrift für Physik D Atoms, Molecules and Clusters, 1, 3. http://dx.doi.org/10.1007/BF01384654
[4]	Hafid, H., Joulakian, B. and Dal Cppello, C. (1993) Theoretical Study of the Differential Cross Section of the Ionization of Hydrogen (2S) by Electron Impact. Journal of Physics B: Atomic, Molecular and Optical Physics, 26, 3415. http://dx.doi.org/10.1088/0953-4075/26/19/028
[5]	Kato, D. and Waanabe, S. (1995) Two-Electron Correlations in Near Threshold. Physical Review Letters, 74, 2443. http://dx.doi.org/10.1103/PhysRevLett.74.2443
[6]	Konovalov, D.A. (1994) Unified Approach to Distorted-Wave (e, 2e) Calculations. Journal of Physics B: Atomic, Molecular and Optical Physics, 27, 5551. http://dx.doi.org/10.1088/0953-4075/27/22/014
[7]	Lahmam-Bennani, A. (1991) Recent Developments and New Trends in (e, 2e) and (e, 3e) Studies. Journal of Physics B: Atomic, Molecular and Optical Physics, 24, 2401. http://dx.doi.org/10.1088/0953-4075/24/10/001
[8]	Bethe, H. (1930) Zur Theorie des Durchgangs schneller Korpuskularstrahlen durch Materie, Annalen der Physik, 397, 325-400. http://dx.doi.org/10.1002/andp.19303970303
[9]	Das, J.N. and Seal, S. (1993) Electron-Hydrogen-Atom Ionization Collisions at Intermediate (5I0-20I0) and High (≥20I0) Energies, Physical Review A, 47, 2978. http://dx.doi.org/10.1103/PhysRevA.47.2978
[10]	Das, J.N. and Seal, S. (1993) Symmetric Scattering Ine±-H Ionization Collisions. Pramana, 40, 253-258. http://dx.doi.org/10.1007/BF02900191
[11]	Das, J.N. and Dhar, S. (1998) Energy Spectrum of Scattered Electrons in K-Shell Ionization of Medium to Heavy Atoms by Relativistic Electrons. Journal of Physics B: Atomic, Molecular and Optical Physics, 31, 2355. http://dx.doi.org/10.1088/0953-4075/31/10/021
[12]	Ghosh Deb S., Roy, S. and Sinha, C. (2009) Multiphoton (e, 2e) Process of Hydrogen Atom in Strong Laser Field. The European Physical Journal D, 55, 591-600. http://dx.doi.org/10.1140/epjd/e2009-00254-x
[13]	Dhar, S. (1996) Electron Impact Ionisation of Metastable 2S-State Hydrogen Atoms. Australian Journal of Physics, 49, 937. http://dx.doi.org/10.0004-9506/96/050937
[14]	Das, J.N. and Dhar, S. (1996) Symmetric Scattering in Electron and Positron Impact Ionization of Metastable 2S-State Hydrogen Atoms. Pramana, 47, 263-269. http://dx.doi.org/10.1007/BF02848527
[15]	Das, J.N. and Dhar, S. (1998) Calculation of Triple Differential Cross-Sections of K-Shell Ionization of Medium-Heavy Atoms by Electrons for Symmetric Geometry. Pramana, 51, 751-756. http://dx.doi.org/10.1007/BF02832607
[16]	Das, J.N. and Dhar, S. (1998a) Energy Spectrum of Scattered Electrons in K-Shell Ionization of Medium to Heavy Atoms by Relativistic Electrons. Journal of Physics B: Atomic, Molecular and Optical Physics, 31, 2355. http://dx.doi.org/10.1088/0953-4075/31/10/021
[17]	Das, J.N. and Dhar, S. (1999) Energy Spectrum of Ejected Electrons in Ionization of Hydrogen Atoms by Electrons. Pramana, 53, 869-875. http://dx.doi.org/10.1007/s12043-999-0121-9
[18]	Dhar, S. and Alam, M.R. (2007) Computation of Triple Differential Cross-Sections with the Inclusion of Exchange Effects in Atomic K-Shell Ionization by Relativistic Electrons for Symmetric Geometry. Pramana, 69, 387-394. http://dx.doi.org/10.1007/s12043-007-0140-3
[19]	Dhar, S. (2008) The Energy Spectrum of Scattered Particles in the K-Shell Ionization of Medium Heavy Atoms by Relativistic Electrons and Positrons with Exchange Effects. Journal of Physics B: Atomic, Molecular and Optical Physics, 41, 15504. http://dx.doi.org/10.1088/0953-4075/41/15/155204
[20]	Vucic, S., Potvliege, R.M. and Joachain, C.J. (1987) Second Born Triple-Differential Cross Sections for the Coplanar Asymmetric Ionization of H(2S) by Fast Electrons. Physical Review A, 35, 1446. http://dx.doi.org/10.1103/PhysRevA.35.1446
[21]	Ghosh, S., Biswas, A. and Sinha, C. (2011) Multiphoton Ionization of a Metastable Hydrogen Atom by Electron and Positron Impact and Charge Asymmetry. Journal of Physics B: Atomic, Molecular and Optical Physics, 44, Article ID: 215201. http://dx.doi.org/10.1088/0953-4075/44/21/215201
[22]	Bransden, B.H. and Joachain, C.J. (1983) Physics of Atoms and Molecules. 2nd Edition, Pearson Education, New York.
[23]	Lewis, R.R. (1956) Potential Scattering of High-Energy Electrons in Second Born Approximation. Physical Review, 102, 537. http://dx.doi.org/10.1103/PhysRev.102.537