Using Multi-Attribute Decision Methods in Mathematical Modeling to Produce an Order of Merit List of High Valued Terrorists ()
1. Introduction
The United States of America is fighting a war against terrorism. The National Strategy for Combating Terror (NSCT) [1] states that the United States Government’s (USG) intent is to obtain victory in the long war against terror, and that the goal and objective in that intent is to defeat terrorists and their organizations. The United States (US) has termed this strategy as the Global War on Terror (GWOT) and the targeting of terrorist organizations’ key personnel is an integral part of this effort.
According to Department of Defense (DoD) doctrine in Army FM 34-8-2 [2] :
Targeting is the process of selecting targets and matching the appropriate response to them, including operational requirements and capabilities. The purpose of targeting is to disrupt, delay, or limit threat interference with friendly Course of Action (COAs).
Human-targeting, the process of selecting a human target exists as a subset of this more general targeting doctrine. This human targeting research is being applied to terrorists.
A common misconception is that human-targeting denotes either a hard-power and soft-power strategy that involves either kinetic or non-kinetic power. Human-targeting is instead intent or objective neutral. It does not specify the type of action taken nor the counterterrorism (CT) objective desired. Human-targeting, rather, re- presents an analytical process that assigns a heuristic value to a target. This assignment of value allows for the prioritization of multiple targets and this prioritization permits CT organizations to direct efforts and allocate resources. Consequently, every government agency, unit, or official whose function serves to counter terrorism remains dependent on the human-targeting process [3] .
To mitigate this risk of terrorist, we propose the development of a systematic method for the conduct of human targeting. We test the proposition using mathematical modeling and multi-attribute decision making tools. These methods are extensively tested and used for finding key network nodes, [4] [5] , and ranking phase targeting of terrorist activities [6] [7] as well as commercial disciplines. These methods may be successfully applied to prioritize human targeting. This research is a preliminary example of this concept.
The current targeting process involves numerous complex and dynamic interactions filled with ambiguities. Minor variations in the process dramatically affect human-targeting decisions producing essentially unpredictable results. In other words, CT organizations may be targeting the wrong (or a less valuable) terrorist. This inefficiency is not only a misuse of intelligence, but wastes limited national resources, which inevitably places lives unnecessarily at risk. Left unaddressed, this critical USG decision-making process with systemic problems could result in a catastrophic intelligence failure [3] .
In previous work by Twedell and Edmonds [8] , they used a series of six linear regression models to ultimately model and obtain a series of terrorist rank orderings. We believe this proposed methodology is better suited to obtain a rank ordering.
2. Proposed Methodology: The Technique of Order Preference by Similarity to Ideal Solution (TOPSIS)
TOPSIS was the result of research and work done by Yoon and Hwang [9] . TOPSIS has been used in a wide spectrum of comparisons of alternatives including: item selection from among alternatives, ranking leaders or entities, remote sensing in regions, data mining, and supply chain operations. TOPSIS is chosen over other methods because it orders the feasible alternatives according to their closeness to an ideal solution [10] .
Napier [11] provided some analysis of the use of TOPSIS for the department of defense in industrial base planning and item selection. For years the military used TOPSIS to rank order the systems’ request from all the branches within the service for the annual budget review process as well as being taught again in as part of decision analysis. Current work is being done to show the ability of TOPSIS to rank order nodes of a dark or social network across all the metrics of social network analysis.
In manufacturing analysis, Wang [12] proposed two methods to improve TOPSIS for multi-response optimization using Taguchi’s loss function. Ozturk and Batuk [13] used TOPSIS for spatial decisions and then linked to geographical information systems (GIS) operations for flood vulnerability. Olson and Wu [14] have shown how TOPSIS may be used for data mining and analysis in credit card score data. Olson and Wu [14] presented a comparison of weights (centroid weights, equal weights, and weights by linear regression) in TOPSIS models using baseball data where their conclusion is that accurate weights in TOPSIS are crucial to success.
In a business setting it has been applied to a large number of application cases in advanced manufacturing processes [15] -[17] , purchasing and outsourcing [18] [19] , and financial performance measurement [20] .
2.1. TOPSIS Methodology
We describe the TOPSIS process is carried out through the following steps.
Step 1
Create an evaluation matrix consisting of 
alternatives and 
criteria, with the intersection of each alter-
native and criteria given as
, giving us a matrix
.
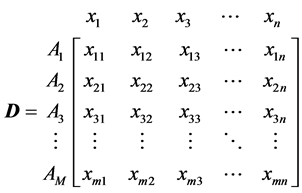
Step 2
The matrix shown as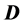 
above then normalized to form the matrix 
using the normalization method
Step 3
Calculate the weighted normalized decision matrix. First we need the weights. Weights can come from either the decision maker or by computation.
Step 3(a)
Use either the decision maker’s weights for the attributes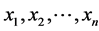 
or compute the weights through the
use Saaty’s (1980) AHP’s decision maker weights method to obtain the weights as the eigenvector to the attributes versus attribute pair-wise comparison matrix.
The sum of the weights over all attributes must equal 1 regardless of the method used.
Step 3(b)
Multiply the weights to each of the column entries in the matrix from Step 2 to obtain the matrix,
.
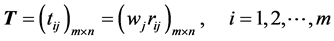
Step 4
Determine the worst alternative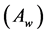 
and the best alternative
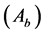: Examine each attribute’s column and select the largest and smallest values appropriately. If the values imply larger is better (profit) then the best alternatives are the largest values and if the values imply smaller is better (such as cost) then the best alternative is the smallest value.
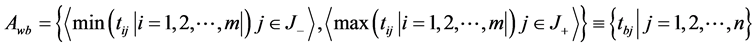
where,
![]()
associated with the criteria having a positive impact, and
![]()
associated with the criteria having a negative impact.
We suggest that if possible make all entry values in terms of positive impacts.
Step 5
Calculate the L2-distance between the target alternative ![]()
and the worst condition ![]()
![]()
and the distance between the alternative ![]()
and the best condition ![]()
![]()
where ![]()
and ![]()
are L2-norm distances from the target alternative ![]()
to the worst and best conditions, respectively.
Step 6
Calculate the similarity to the worst condition:
![]()
![]()
if and only if the alternative solution has the worst condition; and
![]()
if and only if the alternative solution has the best condition.
Step 7
Rank the alternatives according to their value from ![]()
![]()
.
2.2. Sensitivity Analysis
Since AHP, at least in the pairwise comparisons, is based upon subjective inputs using the 9 point scale then sensitivity analysis is extremely important. Leonelli [21] in his master’s thesis, outlines procedures for sensitivity analysis to enhance decision support tools including numerical incremental analysis of a weight, probabilistic simulations, and mathematical models. How often do we change our minds about the relative importance of an object, place, or thing? Often enough that we should alter the pairwise comparison values to determine how robust our rankings are in the AHP process. We suggest doing enough sensitivity analysis to find the “break-point” values, if they exist, of the decision maker weights that change the rankings of our alternatives. Since the pairwise comparisons are subjective matrices compiled using the Saaty’s method, we suggest as a minimum a “trial and error” sensitivity analysis using the numerical incremental analysis of the weights.
Chen [22] grouped sensitivity analysis into three main groups: numerical incremental analysis, probabilistic simulations, and mathematical models The numerical incremental analysis, also known as One-at-a-time (OAT) or “trial and error” works by incrementally changing one parameter at a time, finding the new solution and showing graphically how the ranks change. There exist several variations of this method [23] [24] . Probabilistic simulation employs Monte Carlo simulation [25] that allows random changes in the weights and simultaneously explores the effect on the ranks. Modeling may be used when it is possible to express the relationship between the input data and the solution results.
The decision weights are subject to sensitivity analysis to determine how the affect the final ranking. Sensitivity analysis is essential to good analysis. Additionally, Alinezhad [26] suggests sensitivity analysis for TOPSIS for changing an attribute weight. Equation (1) was developed for adjusting weights based upon a single weight change that we used is:
![]()
(1)
where ![]()
is the future weight of criteria![]()
, ![]()
the current selected weight to be changed, ![]()
the new
value of the selected weight, ![]()
is the current weight of criteria![]()
.
3. Application to Ranking Terrorist
A CT analyst produced both target lists (blue and green) between 2004-2005 [8] . After refinement, the blue target list consisted of 21 terrorists rank-ordered in importance. Additionally, the blue target list assigns the 21 individuals into “Tier” 1 through 5. After refining the second list, the green target list, it contained 31 rank ordered terrorists.
3.1. Criteria Variables: Terrorist Attributes
Based on a review of relevant literature as well as our combined experience of personnel in defense analysis department, we identify 96 critical attributes of terrorists to initially use in the modeling process. We organize these 96 critical attributes to test as predictive variables. Many of these variables were categorical (binary) variables, so we tried to consolidate and refine the number of variables to consider. We felt that initially concentrating on the decision criteria might provide useful information. To maintain organization, we subdivided the criteria into four main categories: Cell Membership/Experience Variables; Other Individual Variables; Worldliness Variables; and SNA/Graph Measures Variables that we refer to as Level 1 criteria. We then broke each of these into sub-criteria with their own respective data that we refer to as Level 2 criteria. The Level 2 criteria were used in the OML process. This is highlighted in Table 1.
We further propose a hierarchy for our analysis.
Objective: Find the Most Dangerous Terrorist
Alternatives: List of terrorists active in 2008
Criteria: Level 1: Level 2 breakdown
Step 1. Obtaining the decision maker weights by level.
Level 1: Priorities: Social Network Analysis, Individual Variables, Cell membership/experience, Worldliness. A begin the pairwise comparisons using our Excel template.
The decision matrix is
The consistency ratio, CR = 0.0372, which is less than 0.1 implies the decision matrix is consistent. The decision weights for Level 1 are:
Next, we proceed to do similar analyses for Level 2. We will take each set of Level 2 variables and obtain their respective weights. In show how we did this in more detail for only one of the Level 1 criteria, Social Networks.
For example, we start with the breakdown of Level 1 social network into specific Level 2 criteria shown to be valid variables and follow the same methods to obtain our decision weights.
The decision maker matrix for these sub-criteria based upon pairwise comparisons is
The resulting weights were found and above matrix is consistent (CR = 0.00318).
We multiply these by the Level 1 weight of 0.55728387 to obtain the weights to be used in our TOPSIS model of
We followed this technique this for all Level 2 variables. We present the results only by criteria main level.
Individual Variables (CR = 0.011)
Cell Membership/Experience (CR = 0.02753)
Worldliness (CR = 0.003)
We apply the TOPSIS seven steps as described in section 2 with the data collected for our terrorists. We present our top 25 terrorist ranking in Table 2.
3.2. Sensitivity Analysis
We apply sensitivity analysis. The sensitivity analysis should be applied to the decision maker weights because they result from subjective pairwise comparison using Saaty’s 9 point process.
We used the suggested sensitivity approach suggested by Alinezhad [26] . In their article they present mathematical formulas for many sensitivity results. We only use the incremental adjusted weights and with the speed of our computer template we quickly changed the weights and obtained new ranking. The formula used is repeated here:
![]()
where ![]()
is the new weight and ![]()
is the original weight of the criterion to be adjusted and ![]()
is the value after the criterion was adjusted. We plotted the top 10 alternatives using several major adjustments in criteria weighting each time insuring a different criterion was the most heavily weighted. It is seen from the graph, Figure 1, that the top 2 did never changed positions.
A complete sensitivity analysis would concern each decision weight being incrementally changed and finding the range over which changes in ranking did or did not occur.
We present a side by side comparison showing the top 25 are still about the same with order adjustments. The top5 are identical and the top 10 are still the top 10 with only terrorist #42, #55, #25 having slight ranking changes as shown in Table 3.
![]()
Table 2. Ranking of the top 25 terrorists.
![]()
Figure 1. Sensitivity analysis for OML of one decision weight.
![]()
Table 3. Updated ranking of terrorists.
This does indicate the model results are sensitive to the decision maker’s pairwise comparisons that are used to find the decision maker weights.
4. Discussion
Based on our analysis, we see substantial benefits of applying our methodology to ordering the targeting of terrorist. However, since our MADM research was primarily focused on explaining and demonstrating this methodology, we first recommend that additional research be conducted in the form of applying this methodology to an active target set that can serve as a further proof of concept. Once our methodology can be verified and validated, we recommend integration into the targeting process of both counter-terrorist focused units and the larger force. We provide a conceptual framework for developing decision support tools for all types of decision problems beyond just the target prioritization problem. We envision an eventual suite of decision support tools and larger decision support systems to assist decision makers with a wide range of problems.
This process provides leadership at all levels with a methodology to produce a key target list among terrorist and terrorist organizations based upon quantitative analysis. We feel that having a quantitative process is better than either a totally subjective approach or a linear regression modeling approach offered by Twedell and Edmond’s research.