Hierarchical Cores Applied to an Analysis of Use of Technologies Level among Higher Education Students in Mexico ()
1. Introduction
The purpose of this work is to statistically analyze the level of use of pocket computing technologies amongst higher education students in Mexico, in order to quantify the degree of influence of marketing and training factors on the demand of calculators with CAS (Computer Algebraic Systems) technology. Experimental work was carried out by González Meneses, M.S. [1] , and included the use of a couple of questionnaires, one for students, and one for teachers, in Technological Institutes in Mexico.
The incorporation of new technologies in Middle and Higher Education is one of the principal purposes for amending syllabuses. Nowadays, there is a wide range of new technologies, from distance education to didactic software for classrooms. Particularly in teaching mathematics, there are many resources to help the teaching-learning experience. One of such resources is the use of calculators with CAS technology (Computer Algebraic Systems). The market for calculators sale is limited to three or four brands who are distributed directly from companies, and there exists the possibility to generate micro and small companies devoted to education and provision of various services such as: didactic aids, syllabus design, and training for teachers, among others, depending on the technological development and implementation of new technologies in the classroom [2] .
This topic has been looked at by J. R. Rodríguez and L. F. Flores López, from the Technological Institute of Los Mochis, Sonora México by means of a didactic proposal for calculation using Texas Instruments Voyage 200 calculators, where the use of CAS technology calculators is shown to improve learning of Differential Calculus [3] . Since Latin America is highly interested in the implementation of new technologies in syllabuses, the following analysis allows us to know factors enabling the proposal of market technologies from regional to national levels, with the potential for making proposals at a Latin American scale [4] [5] .
2. Theoretical Development of Hierarchy by Cores
Based on the fact that factorial correspondence analysis represents, on the same graphic, both sets comprising a tabular correspondence arrangement; sets I of individuals and Q of classes defined for each variable J, and that when such must be taxonomized, a rigid class system must be fixed, then the global and spatial vision provided by factorial analysis allows us establish, through some kind of aggregation method, a type of hierarchy of the data under analysis.
The method herein shown is tributary to three options: 1) calculation of distance between elements where factorial coordinates are known; 2) juxtaposition of mass or weight to each element; and 3) calculation of a distance between element classes, depending on an aggregation criterion based on cores. Since our data includes factorial values related to Q classes, we shall retain a small number of A cardinality factors, not higher than 75% of factorial data.
Let us define factorial set of values through set: , with which it is possible to cal-
, with which it is possible to cal-
culate many tabular arrangements for distances between elements. In our case, we shall introduce the following distance. Let q and q' be two classes of a variable j Î J such that q and q' Î Q. Classes q and q' belong to a normed factorial space with a fixed set of coordinates. If  then (F, d) is a metric space. Factorial distance between
then (F, d) is a metric space. Factorial distance between 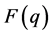 and
and  is the addition of lengths of projections of line segment between factorial values on the axes system. This is mathematically expressed as follows:
is the addition of lengths of projections of line segment between factorial values on the axes system. This is mathematically expressed as follows:
 (1)
(1)
where q and q' are classes of variable j Î J, d is the distance between classes, a is the axis, A is the set of axes and 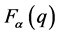 and
and  are factorial values of classes.
are factorial values of classes.
In accordance with the second option of the aggregation method defined, the distance between classes is juxtaposed by inertia l of the set of dots along axis a, which is represented by the own value related to the corresponding axis, because of this Equation (1) may be re-expressed as follows:
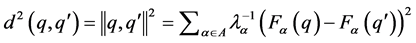 (2)
(2)
where q and q' are the classes of variable j Î J, d is the distance between classes, a is the axis, 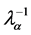 is the inverse of distance between classes on axis a and
is the inverse of distance between classes on axis a and 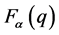 represents factorial value of class q on axis a [6] .
represents factorial value of class q on axis a [6] .
Once the distance between values has been defined, the diameter index of nodes of classification n of such hierarchy must be calculated, through:
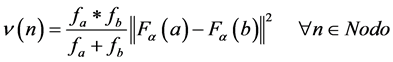 (3)
(3)
where a and b are barycenter’s of elements of the index, fa and fb are the mass in a and b barycenter’s, and 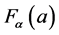 and
and 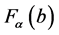 are factorial values of a and b barycenter’s. In addition,
are factorial values of a and b barycenter’s. In addition, 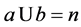 and
and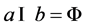 .
.
Every time, the distance between elements that are hierarchized must be recalculated with those to be hierarchized, because of this the following diameter index  is:
is:
![]() (4)
(4)
where ![]() is diameter index,
is diameter index, ![]() and
and ![]() are masses of a and b barycenter’s,
are masses of a and b barycenter’s, ![]() and
and ![]() are factorial values of a and b barycenter’s, and
are factorial values of a and b barycenter’s, and ![]() is the square root of total distance of the A set of dots, along axis a.
is the square root of total distance of the A set of dots, along axis a.
Now, from Equation (3) it may be seen that the addition of values of diameter indexes is equal to the addition of total distance l of the set of dots along a axis, that is:
![]() (5)
(5)
where ![]() diameter is index and la is total distance of the set of axes. From Equation (4) it may be seen that the addition of values of diameter indexes is equal to A’s cardinality.
diameter is index and la is total distance of the set of axes. From Equation (4) it may be seen that the addition of values of diameter indexes is equal to A’s cardinality.
![]() (6)
(6)
The Algorithm
Classification algorithm looks for two minimum values of the table of factors of classes to be hierarchized.
![]() (7)
(7)
From this aggregation, defined as![]() , a new partition or core of the set of Q classes must be updated
, a new partition or core of the set of Q classes must be updated
making:![]() . Distances between this new element k and
. Distances between this new element k and ![]() are recalculated, showing the following minimum value of the factors table, through Formula (3), thus making
are recalculated, showing the following minimum value of the factors table, through Formula (3), thus making![]() . The minimum of the new table is investigated, aggregated and a new partition is updated below. The above is carried out until there is no more than the two last cores to be added, taking into account that the link is the base set [7] and [8] .
. The minimum of the new table is investigated, aggregated and a new partition is updated below. The above is carried out until there is no more than the two last cores to be added, taking into account that the link is the base set [7] and [8] .
Theorem Cores Optimal Criterion. If aggregation cores are groups of factors with same cardinality and W the space of cores, optimal election criterion is:
![]()
where L is the total set of cores, Ai is the ith core containing a certain number of objects of P population.
Demonstration. Let![]() ,
, ![]() be the ith core containing q elements of population.
be the ith core containing q elements of population. ![]() is partition of space Winto k-classes. Let
is partition of space Winto k-classes. Let ![]() be the set of kth cores and
be the set of kth cores and ![]() the set of parti- tions of W cores space into classes.
the set of parti- tions of W cores space into classes. ![]() measures dissimilarities between core Ai and class
measures dissimilarities between core Ai and class![]() . Based on the above, the principal problem is to look for a
. Based on the above, the principal problem is to look for a ![]() and a population
and a population ![]() that minimize d dissimi- larity.
that minimize d dissimi- larity.
Let ![]() be a measure for dissimilarities between couples of individuals or classes. Let us suppose that:
be a measure for dissimilarities between couples of individuals or classes. Let us suppose that:
![]()
where X and Y are parts of the set of W individuals, then:
![]()
In case that cores are groups of individuals, the algorithm shall be specified, since such is basedon choosing two functions: assignation function and representation function.
For the assignation function, given the cores![]() , partition
, partition ![]() deducted is defined by:
deducted is defined by:
![]()
In case of equality, ![]() shall be assigned to the lowest index class. Partitions P thus deducted from L are
shall be assigned to the lowest index class. Partitions P thus deducted from L are
shown by![]() , where f is an application of
, where f is an application of ![]() in
in![]() ; that is:
; that is:![]() , and it is called assignation
, and it is called assignation
function.
For the representation function, given partition P, ![]() cores are deducted as:
cores are deducted as:
![]() (8)
(8)
In order to ensure the unit of Ai, the set of q elements of W space minimizing![]() , ex- ists and is unique. Therefore, the representation function exists.
, ex- ists and is unique. Therefore, the representation function exists.
QED
Observation 1. It is possible to define representation function from a given![]() , such that
, such that![]() , since Ai are defined from
, since Ai are defined from ![]() with (8).
with (8).
Observation 2. With the Theorem of Cores Optimal Criterion and Observation 1, the algorithm implies alter- natively implementing f and ![]() from a partition or kth core randomly estimated. Every iteration implies ap- plying function f from and
from a partition or kth core randomly estimated. Every iteration implies ap- plying function f from and ![]() element or function
element or function ![]() from a
from a ![]() element.
element.
3. Application
The attachment shows the questionnaire developed for application on the student population. The survey was partially national (center and north of the country) due, mainly, to the features of the student population (at this education level, the student population in Mexico is 10,803,868—both males and females—between 18 and 22 years old) and null financial support available for calculation of a probabilistic sample and its application (trip expenses of specialized survey personnel). The questionnaire was applied with the consent of the student, and students came from various higher education institutions (public and private) professors interested in the topic were also surveyed [9] .
3.1. Data under Analysis
Data used and analyzed is a data table![]() , with tabular arrangement:
, with tabular arrangement: ![]() [10] ,
[10] ,
where I is the set of questionnaires with cardinality 1839 and the set of questions with cardinality 16. The definition of variables is shown in chart I.2 of the Annex, and its frequency structure is the following.
The use of the questionnaire with students of bachelor degrees of the public education system shows a log- normal distribution, the most participative students where those of mechatronics, while the less participative were those of mathematics. This is rather logical, since seeing a mathematician with a calculator is as horrible as seeing a software developer exploring a computer with a screwdriver. The semester variable shows a bimodal behavior where the most participative are freshmen. The variable grouping current type of calculator of the stu- dent, shows a leptokurtic distribution, where Casio calculators have the highest percentage, 55.07%, while Sharp calculators have the lowest percentage, 6.65%. The place of purchase of equipment variable shows the same leptokurtic distribution, where department stores have the highest percentage of sales of such equipment’s. The influence on purchase by brand shows a behavior not defined. To study it, it has been defined in percentages where 50.9% of people in the survey answers that the name of the equipment influences 80% the purchase. The influence on purchase, due to its technical features, shows a distribution J, where 66.27% answers that it does influence in 80% [11] .
3.2. Correlations
Since it is a well-known theory, its development is not shown here, we only mention that the calculation of cor- relations or degree of association among variables has been carried out based on ordinary Euclidian distance ![]() among variables j and j'. Besides, it must be remembered that, if two variables are strongly correlated, those are near to each other
among variables j and j'. Besides, it must be remembered that, if two variables are strongly correlated, those are near to each other ![]() or, on the contrary, as far as possible from each other
or, on the contrary, as far as possible from each other![]() , as linear relationship linking them is direct or inverse, and that when
, as linear relationship linking them is direct or inverse, and that when ![]() those are at middle distance or that j and j'
those are at middle distance or that j and j'
are orthogonal. In box (k, j) there is![]() . The kth diagonal term is
. The kth diagonal term is![]() . It should be noticed that symmetry of matrix:
. It should be noticed that symmetry of matrix:![]() . Regarding interpretation, variables with strongest correlation
. Regarding interpretation, variables with strongest correlation
are brand and price, with 0.438, Table 1. Calculator brand and type of calculator, with −0.311, are correlated below.
Table 2 shows values obtained from the multiple correlation analysis of variables under study. Here, no vari- able shows a high multiple correlations. Most variables multiply correlated to 0.5 correlative values are: influ- ence of make, price and type of calculating machine.
![]()
Table 1. Correlations between variables of use of technologies level among higher education students.
![]()
Table 2. Multiple correlations of variables under study.
3.3. Principal Components Analysis
Let us now see the results of the Principal Component Analysis, PCA, on a tabular arrangement of gross data ![]() (1839 ´ 16) on a correlations matrix. The theoretical description of the method is shown in [12] , pp. 65- 78.
(1839 ´ 16) on a correlations matrix. The theoretical description of the method is shown in [12] , pp. 65- 78.
Interpretation of correlations circle 1 - 2, Figure 1(a) and Figure 1(b), shows that the first two principal components explain 11.0% and 10.5%, respectively, that is, the first correlations circle contains 21.5% of gross data, and shows a contraposition between the type of calculator currently owned by a student (without knowing which type of calculator it is) and the semester he/she is in (without knowing in whish semester he/she is enrolled), versus brand, technical features of the equipment, price (every figure in percentage), and how much he/she uses the applications on his/her equipment. Regarding the second correlations circle, where the principal components 1 - 3 intervene, and which explains 18.9% of gross data (10.5% and 8.4%, respectively), it shows contraposition regarding the first component of type of calculator currently owned by the student (without knowing which type of calculator it is) and the information consulted before the purchase (without knowing if such includes brochures, recommendation or Internet), versus brand, technical features of the equipment, price (every figure in percentage), how much he/she uses the applications of his/her equipment, the type of calculator he/she currently owns and the calculator he/she would like to buy, as well as the knowledge he/she has about Texas Instrument calculators.
3.4. Hierarchical Ascending Classification with Euclidean Distance
The hierarchical dendrogram, built based on Euclidean distance, is composed of 3 branches, Figure 2. Reading and interpretation run from right to left, for hierarchical reasons [13] .
![]() (a)
(a)![]() (b)
(b)
Figure 1. Correlations circle. a) Principal Components 1 - 2; b) Principal Components 1 - 3.
![]()
Figure 2. Hierarchical dendrogram of the use of technologies in higher education based on Euclidean distance (see Table 2, attachment, for definition of variables).
The dendrogram shows two aggregations of variables, the first one agglutinates variables making the first one a principal component: brand, price, technical features of the equipment and how much he/she uses the applica- tions of his/her equipment. The second aggregation is composed by the remaining variables under study.
3.5. Factorial Analysis on Gross Data
The factorial method chosen to describe data under study is the Correspondence Analysis, CA, method. This method allows a direct search for the best simultaneous representation of sets under study; I questionnaires completed by students, and J variables describing the use of micro computing technologies in teaching practice. The CA applied to gross data ![]() has the following factorial features: variances on the principal three axes or own values are: X1 = 0.0502, X2 = 0.0341 and X3 = 0.0307, while percentages of habit explained by such axes are, respectively: 35.5%, 24.1% and 21.7%. The first factorial plane 1 - 2 has no defined shape and origin mass center. Variables of highest importance are brand, price, technical features of equipment and use of applications, with values ranging from 21.18 through 24.81. The first factorial axis is defined by the four variables mentioned above, of the highest importance in this study. The second factorial axis is defined by technical features in the purchase of the equipment and in its use. The third factor is defined by brand and price of the equipment.
has the following factorial features: variances on the principal three axes or own values are: X1 = 0.0502, X2 = 0.0341 and X3 = 0.0307, while percentages of habit explained by such axes are, respectively: 35.5%, 24.1% and 21.7%. The first factorial plane 1 - 2 has no defined shape and origin mass center. Variables of highest importance are brand, price, technical features of equipment and use of applications, with values ranging from 21.18 through 24.81. The first factorial axis is defined by the four variables mentioned above, of the highest importance in this study. The second factorial axis is defined by technical features in the purchase of the equipment and in its use. The third factor is defined by brand and price of the equipment.
3.6. Classes of Variables’ Cut and Its Factors
Since the PCA and CA used on data do not show any relationship whatsoever between variables, it was necessary to fragment the first data table in a class table, [12], Chapter III. Let
![]()
that is, for every element I in the set of answers to variables determining the level of use of technologies in the practice of teaching mathematics, there is a set of variables J whose elements each contain a subset C called
classes cr, such that for each variable there are tabular arrangements ![]() with whole values
with whole values
between 1 and m. Ranges in which variables were fragmented are shown in Chart A.2, Annex I.
A table of generalized contingency has been created, based on the classes table ibid p. 28, Chapter III. The tabular arrangement created has a dimension of 1839 ´ 67 elements. Classes of highest importance in this study are: has not taken courses to use his/her calculator; technical features and price influence on purchase from 25% to 50%; already has a scientific calculator and is not interested in purchasing a new one. The less important ones in the study are: chemistry, materials and pure mathematics students, which is rather logical, since they are students of scientific specialty who do not need a calculator to carry out their professional studies.
The first factorial plane of the table in classes of the level of use of technologies among students of higher education has only 8% of data and has a slight parabolic structure, Figure 3. The first factor is composed by students of fourth semester, who use Texas Instruments symbolic calculators, students of mechatronics, who
![]()
Figure 3. First factorial plane of use of technologies among higher education students in Mexico.
have taken courses to use such and know their benefits. The second factor is composed by influence of brand, weight and technical features of calculators for all percentages. The third factor is composed by students of fifth and sixth semester of all careers, who need an additional graph maker.
4. Use of Technologies Dendrogram
The hierarchical dendrogram built under the aggregation criterion of the central moment of order two, is com- posed by five branches, Figure 4. Reading and interpretation go from left to right; the hierarchical level scale has a maximum of 16 hierarchical units and the symbol near the 15th unit means a jump of scale units. In the bottom of the hierarchical structure the definition of class are briefly recorded.
The first hierarchical branch is composed of the second factor of factorial analysis, as well as some classes which do not show up in the analysis, such as the mechatronics and computing students then in the fourth and sixth semester of the career, who know how to use the equipment’s under analysis. The second hierarchical branch is composed by three sub-branches: first, the most important classes in this study, that is, the chemistry and industrial engineering students who have a scientific calculator in first semester. The second sub-branch is composed by electronic, foods and civil engineering students in third semester, who know the benefits of such equipment’s and are certain that the school and the teachers promote their use and purchase. The third sub-branch is composed by mechanics, applied mathematics and industrial chemistry students, who get the tech- nical information with friends and show that the influence of price is 75%. The fourth and fifth hierarchical branches are rather a single branch, since their final aggregation comes after the cut and, put together, constitute the first factor.
5. Discussion of Results
This work is presented in accordance with its development. The theory developed on hierarchical cores is shown, where the method shown is tributary to three options: 1) calculation of distance between elements where factorial coordinates are known; 2) juxtaposition of mass or weight to each element; and 3) calculation of a distance between element classes, depending on an aggregation criterion based on hierarchical cores.
![]()
Figure 4. Dendrogram of use of technologies among higher level students.
Development of a proper data collection vehicle and its pilot test, provide enough data for national application and subsequent statistical analysis which allows constructing hierarchical cores based on an ascending hierar- chical classification.
Results provided by linear statistical part are not enough to obtain conclusions on factors influencing quanti- fication of CAS calculator’s demand, basic fact influencing theoretical development. The first factorial plane of technologies use by higher education students in Mexico accounts for the path of classes making factors, which subsequently define hierarchical cores.
6. Conclusions
From the point of view of theory developed, it may be seen that from various starting points, the problem of looking for stable classes may be resolved. Starting points may be chosen by the user, with the help of a hierarchical classification.
The theorem demonstrated and called Cores Optimal Criterion Theorem allows implementing f and ![]() functions from a kth core randomly estimated with the algorithm.
functions from a kth core randomly estimated with the algorithm.
The purpose of analyzing and defining factors influencing the use of new technologies in the practice of teaching mathematical calculations in Mexico is achieved, since, as has been explained in the statistical analysis of data, it has been observed that the most important classes in this study are: 1) no courses to use the calculator; influence of technical features and price on the purchase; 2) 20% to 50% already has a scientific calculator and is not interested in purchasing a new one. The less important classes in this study are: chemistry, materials, and pure mathematics students. This is rather logical, since such are students of scientific specialty who do not need a calculator to carry out their professional studies.
The first factor is composed by mid-term engineering students using Texas Instruments symbolic calculators, who have taken courses to use them and know their benefits well. The second factor is composed by the influ- ence of brand, weight and technical features of such calculation equipment’s. The third factor is composed by students in the second half of the career, who need an additional graph maker.
From the point of view of hierarchical classification, the first branch is composed by the second factor of fac- torial analysis, as well as some classes which do not show up in the analysis, such as the engineering students who are halfway through their degree, who know how to use the equipment under analysis. The second hierar- chical branch is composed by three sub-branches: first, the most important class in this study is the engineering students who have a scientific calculator in first semesters. The second sub-branch is composed by engineering students in third semester, who know the benefits of such equipment’s and are certain that the school and the teachers promote their use and purchase. The third sub-branch is composed by engineering students, who get the technical information with friends and show that the influence of price is 75%.
Acknowledgements
I thank the disinterested collaboration and datacontribution of Myrna E. González Meneses, M.S., to carry out this multidimensional data analysis. I also acknowledge the contribution for research project recorded at the National Polytechnic Institute. Mexico with number SIP-20130585.
Annex I Questionnaire
Data obtained from this questionnaire aims at determining the level of use of new technologies in teaching mathematics and developing a marketing proposal for some calculator models Texas Instruments.
BRAND PRODUCT
Bachelor’s degree in engineering: ____ Semester: ____ Age: _______ Do you work? ______
1. What calculator do you have now? £ Texas Instruments £ Casio £ HP £ Sharp £ Other:
2. Where did you buy your current calculator?
PLACEMENT OF PRODUCT
£ I don’t have one £ Authorized distributor £ Department store £ From an acquaintance £ Other
3. What percentage influences you to buy a calculator?
Brand product ___________ (0% - 100%) BRAND PRODUCT
Price _______________________ (0% - 100%) PRICE
Technical features________ (0% - 100%) USE OF PRODUCT
4. Have you taken any course to use a calculator? £ Yes £ No TRAINING
5. Choose the type of calculator you currently have (no matter the make, only the features of the model)
USE OF PRODUCT
![]()
![]()
![]()
6. How many of the calculator’s applications do you use? TRAINING
Basic operations, statistics ____________ (0% - 100%)
Basic operations, statistics, graph making, programming, matrixes ____________ (0% - 100%)
Basic operations, geometry, graph making, programming, differential and integral calculus, statistics, finance, word processor, simultaneous equations, polynomial roots, ______(0% - 100%)
7. When you buy a calculator, which data do you consult? ADVERTISEMENT
£ Pamphlets £ Acquaintances £ School £ Internet £ Other _______________
8. Which type of calculator would you like to buy (even if you already have one)? PRICE
![]()
![]()
9. If you would buy any of the above calculators, how would you pay it? £ Cash £ Credit
SELLING PLANS
10. Mark if your teachers
£ Promote use of graph making calculators or symbolic calculation calculators in any subject.
£ Always £ Sometimes £ Never
PROMOTION
11. Do you know the benefits offered by Texas Instruments regarding technical support?
£ Yes £ No
ADVERTISEMENT
12. Does your school promote the visit or calculator promoters? £ Yes £ No
PROMOTION, SELLING PLANS
Table Annex I.1. Statistical parameters of variables under study.
Table Annex I.2. Classes’ cut of variables of use of technologies in higher education.