Ternary Zero Correlation Zone Sequence Sets for Asynchronous DS-CDMA ()
1. Introduction
In Code Division Multiple Access (CDMA) systems, the number of spreading sequences determines the number of users and their correlation properties have a significant effect on anti-interference performance of the system [1] . Different types of codes used in communications systems have been studied in order to reduce Multiple Access Interference (MAI) [2] [3] . For an interference-free communication, spreading codes should have zero auto-correlation and zero cross-correlation functions at out-of-phase state. So, spreading sequences with good cor- relation properties can be used to improve the performance of CDMA systems [3] . One class of spreading se- quences called Zero Correlation Zone (ZCZ) sequences possesses good correlation properties but only in spe- cific zones called Zero Correlation Zone (ZCZ). There are several intensive studies of CDMA systems using ZCZ sequences sets [1] [3] -[6] . Various classes of ternary ZCZ sequences sets have been constructed [3] [4] and [7] -[13] . Ternary ZCZ sequences have the advantage over binary ZCZ sequences that is, for a given sequence length, the set has longer 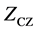 lengths and more sequences, and we may employ such hardware in binary ZCZ sequence sets system [3] . Any ternary ZCZ sequences set TZCZ
lengths and more sequences, and we may employ such hardware in binary ZCZ sequence sets system [3] . Any ternary ZCZ sequences set TZCZ 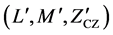 could be characterized by the sequence length
could be characterized by the sequence length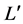 , the number of sequences
, the number of sequences 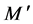 and the zero correlation zone length
and the zero correlation zone length . An optimal ZCZ set is the one that provides the maximum number of codes for a given
. An optimal ZCZ set is the one that provides the maximum number of codes for a given 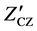 and sequences lengths. The pro- posed ternary ZCZ sequences set with TZCZ
and sequences lengths. The pro- posed ternary ZCZ sequences set with TZCZ 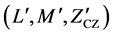 is derived from a binary ZCZ sequence set with BZCZ
is derived from a binary ZCZ sequence set with BZCZ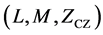 . When compared with previous works on ternary ZCZ sequence sets [3] [4] and [7] -[13] , our proposed ZCZ sequence set approaches optimality.
. When compared with previous works on ternary ZCZ sequence sets [3] [4] and [7] -[13] , our proposed ZCZ sequence set approaches optimality.
The remainder of the paper is organized as follows.
After a review of preliminary considerations in Section 2, the proposed design for sequence construction is explained in Section 3. Example of new ZCZ sequence sets are presented in Section 4. The properties of the proposed sequence sets are explained in Section 5. In Section 6, we consider the performance of the proposed ternary ZCZ sequence sets compared with those in [3] and [10] for the asynchronous DS-CDMA system in both AWGN and nonselective fading with AWGN noise channels. At the end, we draw the concluding remarks.
2. Preliminaries
2.1. Definition 1
For a pair of sequences Xj and Xv of length L, the aperiodic correlation function (ACF) 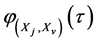 is defined as follows [14] [15] :
is defined as follows [14] [15] :
 (1)
(1)
The periodic correlation function (PCF) between Xj and Xv at a lag 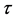 is determined by [15] [16] :
is determined by [15] [16] :
 (2)
(2)
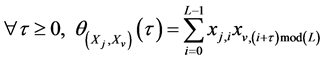 and (3)
and (3)
2.2. Definition 2
A set of M sequences 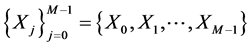 is called zero correlation zone sequence set if the periodic correlation functions satisfy [15] [16] :
is called zero correlation zone sequence set if the periodic correlation functions satisfy [15] [16] :
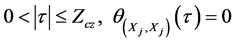 (4)
(4)
and
 (5)
(5)
3. Proposed Sequence Construction
The construction procedure of the new ternary sequence sets is presented. The construction is accomplished across the following three steps:
Step 1: The jth row of the Hadamard matrix H of order n is indicated by![]() . A set of 2n sequences dj, each of length 2n, is constructed as follows [17] :
. A set of 2n sequences dj, each of length 2n, is constructed as follows [17] :
For ![]()
![]() (6)
(6)
![]() (7)
(7)
Step 2: For the first stage![]() , and for a fixed integer value n, we can generate, based on the schema for sequence construction in [15] , a series of sets
, and for a fixed integer value n, we can generate, based on the schema for sequence construction in [15] , a series of sets ![]() and
and ![]() of 2n sequences as follows:
of 2n sequences as follows:
Both sequences sets ![]() and
and ![]() are constructed from the sequences set
are constructed from the sequences set![]() . A pair of se-
. A pair of se-
quences ![]() and
and ![]() of length
of length ![]() are constructed by applying the interleaving operation of a sequence pair
are constructed by applying the interleaving operation of a sequence pair ![]() in Equations (6) and (7) [17] and a pair of sequences
in Equations (6) and (7) [17] and a pair of sequences ![]() and
and ![]() are con- structed by the interleaving operation of a sequence pair
are con- structed by the interleaving operation of a sequence pair![]() ,
, ![]() and from padding Z, which are zeros of length K, as follows:
and from padding Z, which are zeros of length K, as follows:
For![]() ,
,
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
The length of a pair sequences ![]() and
and ![]() in Equations (10) and (11) is
in Equations (10) and (11) is ![]() and the member size of a pair sequence sets
and the member size of a pair sequence sets ![]() and
and ![]() is
is![]() .
.
Step 3: For![]() , we may recursively build a new series of sets
, we may recursively build a new series of sets ![]() and
and ![]() by interleaving
by interleaving
actual sets ![]() and
and ![]() respectively. Sets
respectively. Sets ![]() and
and ![]() are generated as follows:
are generated as follows:
For![]() ,
,
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
The length of both sequences ![]() and
and ![]() in Equations (12) and (13) is equal to
in Equations (12) and (13) is equal to ![]() [17] and the length of both sequences
[17] and the length of both sequences ![]() and
and ![]() is equal to
is equal to![]() .
.
4. Example of Construction
1) For ![]() and
and![]() , the
, the ![]() is generated as follows [17] :
is generated as follows [17] :
![]()
![]()
![]()
![]()
Figure 1 shows the periodic auto-correlation function (PACF) ![]() given in Equation (3) of
given in Equation (3) of![]() , and Figure 2 shows the periodic cross-correlation function (PCCF)
, and Figure 2 shows the periodic cross-correlation function (PCCF) ![]() given in Equation (3) of
given in Equation (3) of ![]() with
with![]() .
.
The PACF and PCCF confirm that ![]() is a ZCZ (32, 4, 4) sequence set.
is a ZCZ (32, 4, 4) sequence set.
2) For ![]() and
and![]() , the proposed
, the proposed ![]() is generated as follows:
is generated as follows:
![]()
![]()
![]()
![]()
Figure 3 shows the PACF of![]() , and Figure 4 shows the PCCF of
, and Figure 4 shows the PCCF of ![]() with
with![]() .
.
The PACF and PCCF confirm that ![]() is a TZCZ (64, 4, 12) sequences set.
is a TZCZ (64, 4, 12) sequences set.
5. The Features of the Proposed Sequence
The Binary ZCZ sequence set with BZCZ ![]() is optimal or approach optimal binary ZCZ sequences [17] . The length of
is optimal or approach optimal binary ZCZ sequences [17] . The length of ![]() in Equations (14) and (15), equals
in Equations (14) and (15), equals![]() , is twice that of
, is twice that of ![]() in Equations (10) and (11). Let
in Equations (10) and (11). Let ![]() and
and![]() , the proposed ternary ZCZ sequence set with TZCZ
, the proposed ternary ZCZ sequence set with TZCZ ![]() is derived from the binary ZCZ sequence set BZCZ
is derived from the binary ZCZ sequence set BZCZ![]() . If the obtained ternary ZCZ sequence set is op- timal, it satisfies the ratio
. If the obtained ternary ZCZ sequence set is op- timal, it satisfies the ratio ![]() [9] [10] .
[9] [10] .
If ![]() (the first iteration), the obtained sequence set is an optimal ternary ZCZ sequence set.
(the first iteration), the obtained sequence set is an optimal ternary ZCZ sequence set.
Proof: Let![]() , we calculate the following ratio:
, we calculate the following ratio:
![]()
If![]() ,
, ![]() ,
,![]() .
.
If ![]() and the number
and the number ![]() of the padded zeros tends to the infinite, the obtained TZCZ sequences set (see Table 1 for n = 2) is asymptotically optimal.
of the padded zeros tends to the infinite, the obtained TZCZ sequences set (see Table 1 for n = 2) is asymptotically optimal.
Proof: ![]() and
and ![]()
Noted that for this case, after spreading, the power of the symbol will decrease sharply, it is mandatory to compensate it, but this requirement increases Peak-to-Average Power Ratio (PAPR) and dynamic range of the transmitted signal [3] .
From Table 2 we can see that the proposed sequence set in this paper can provide certain benefits. The length of sequences and ZCZ will increase together while the number of sequences remains unchanged.
In the asynchronous DS-CDMA system, the time delay is typically in some chips, and for this, we can in- crease the ZCZ to reduce MAI, but the member size will be relatively petty.
For a given member size M, we can find various sets of sequences with different lengths L and ZCZ. As an example, assuming that M = 8 and K = 3 (see Table 3 for n = 4), we can draw upper bounds of our code per- formance and compare it with the Hayashi’s approach.
The Hayashi’s ternary sequence sets ZCZ-![]() in [10] based on Hadamard matrix, the
in [10] based on Hadamard matrix, the
member size of the sequence set is ![]() of theoretical upper bound.
of theoretical upper bound.
It is clear from Table 3, the proposed construction is one of the better type in the constructions mentioned in Table 2. Compared with the Hayashi’s work, our proposed, in all cases, is optimal or approximate optimal ZCZ
![]()
Table 1. The parameters of the proposed ternary ZCZ sequence set and the ratio R.
![]()
Table 2. Comparison of three types of ZCZ sequence sets.
![]()
Table 3. The parameters of two constructions of ternary ZCZ sequence sets.
sequence set. Consequently it has a higher ZCZ and better performance parameter R than that given by Hayashi’s construction.
6. The Performance of the Asynchronous DS-CDMA System Using the Proposed Ternary ZCZ Sequence Set
In this section, we consider the performance of the proposed ternary ZCZ sequence set used as spreading se- quences for the DS-CDMA system shared by M asynchronous users simultaneously. In order to show this per- formance, the BER of an asynchronous DS-CDMA system over a frequency non-selective fading channel with AWGN noise estimated in [18] [19] is used:
![]() (16)
(16)
where P is the common received power, T is the symbol duration, the Q function in Equation (16) is given by
![]() [20] , the term
[20] , the term ![]() is the variance for the AWGN noise, the term
is the variance for the AWGN noise, the term ![]()
denote the faded component power from the user i and ![]() is the global (non-faded) interference MAI power for the required i-th user.
is the global (non-faded) interference MAI power for the required i-th user.
Let![]() , the BER of an asynchronous DS-CDMA system over AWGN channels is:
, the BER of an asynchronous DS-CDMA system over AWGN channels is:
![]() (17)
(17)
The MAI variance for the required i-th user can be calculated as [18] [19]
![]() (18)
(18)
where ![]() in Equation (18) is the interference term caused by all other users m except the user i. The term
in Equation (18) is the interference term caused by all other users m except the user i. The term ![]() from Equation (1) can be written as [18] [19] :
from Equation (1) can be written as [18] [19] :
Let ![]()
![]() (19)
(19)
In Figure 5 and Figure 6 we compared the BER performance of the asynchronous DS-CDMA system em- ploying Hayashi’s TZCZ (40, 8, 3), Hayashi’s TZCZ (20, 8, 1) and the proposed ternary ZCZ sequence sets with parameter TZCZ (32, 8, 3).
At BER = 10−4 in Figure 5, the system using constructed TZCZ can attain 01 dB and 06 dB gains over the same system employing Hayashi’s TZCZ (40, 8, 3) and Hayashi’s TZCZ (20, 8, 1) in AWGN respectively.
The BER performance, in Figure 6 was simulated assuming a frequency nonselective fading channel with AWGN noise with the common faded power ratio![]() . As we can see in Figure 6, the proposed TZCZ sequence sets show better performance than Hayashi’s TZCZ sequence sets.
. As we can see in Figure 6, the proposed TZCZ sequence sets show better performance than Hayashi’s TZCZ sequence sets.
At BER = 0.0015 the system can attain 01 dB and 10 dB gains over the system employing Hayashi’s TZCZ (40, 8, 3) and Hayashi’s TZCZ (20, 8, 1) respectively. The amelioration over comparable Hayashi’s ternary ZCZ sequences is due to the correlation properties of the proposed ternary sequence set.
7. Conclusion
A new construction method to create ternary ZCZ sequences set based on binary ZCZ sequence sets was pro- posed in this paper. This ternary ZCZ sequences set is either optimal or asymptotically optimal and their con-
![]()
Figure 5. BER performance of Asynchronous DS-CDMA for dif- ferent TZCZ over AWGN.
![]()
Figure 6. BER performance of Asynchronous DS-CDMA for dif- ferent TZCZ over a Fading AWGN.
struction is more flexible than other ternary ZCZ constructions. The asynchronous DS-CDMA using the pro- posed ternary ZCZ sequences shows better BER performance in both AWGN and frequency non-selective fad- ing channel with AWGN noise.