Detection of Edge with the Aid of Mollification Based on Wavelets ()
1. Introduction
In the present paper, we take up the problem of detecting an edge for a function involving noise. For a function, an edge is a point where the derivative is maximum or minimum.
Calculation of the derivative of a function is an ill-posed problem, in the sense that, when a function involes noise, the derivative emphasizes the noise. In the method of mollification [1] to cope with the problem, the data involving noise is mollified before the derivative is taken. When a function involving noise,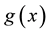 
, is given, Murio [1] proposed to use
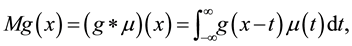
as the mollified function where the mollifier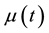 
is a Gaussian probability density function.
In our preceding papers [2] -[4] , the mollification based on wavelets is studied for the problem of calculating the derivative or the fractional derivative (fD) of a function involving noise, and an estimation of the error of approximation is given in terms of fD. In [4] , we chose three mollifiers based on wavelets, by which the noise in a noisy data is removed and the Gibbs phenomenon is not observed.
In the problem of detecting an edge of an image, Mathieu et al. [5] [6] proposed the use of the CRONE detector. For a function, an edge is a point where the derivative is maximum or minimum. In order to make the point clearer, they propose to use the difference of an fD in increasing variable and an fD in decreasing variable, when there exists no noise. We note that the difference is equal to the Riesz fD of the derivative. We shall call that detector the primitive CRONE fD detector. The calculation of fD is an ill-posed problem, and this is powerless when there exists noise. When there exists noise, they propose to use the fractional integral (fI), to reduce noise. If we use fI, the peak of the derivative is made broad, compared with the simple derivative of the mollification. In practice, they truncate the function to be convoluted in the calculation of fI, and it is not seen to be a direct application of fI. They call this detector also as the CRONE detector. We shall not discuss that method in the present paper.
In the present paper, we study the application of mollification to the Riesz fD of the derivative, for the case when there exists noise. The results are compared with the derivative calculated by the method of mollification given in [3] . The calculation is done by using the mollifiers proposed in [4] .
In Section 2, we review the preceding papers [2] -[4] . In Section 3, we numerically study the edge detection by applying the our method of mollification to the calculation of a function involving noise. In Section 4, we recall the definitions of fDs and the primitive CRONE fD detector. In Section 5, we study the application of the primitive CRONE fD detector to a function without noise. In Section 6, we numerically study the mollification of a function involving noise, and the application of the primitive CRONE fD detector to it. Section 7 is for conclusion.
We use notations 
and 
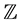to represent the sets of all real numbers and of all integers, respectively. We
also use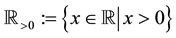
, and 
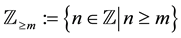for
. For a function
, that is
integrable on 
in the sense of Lebesgue, and its Fourier transform is denoted by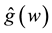 
or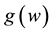
, so that
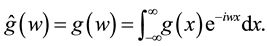
We denote the Heaviside step function by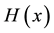
, so that 
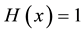for 
and ![]()
for![]()
.
2. Mollification Depending on a Scale
In the present study of mollification, we choose a mollifier ![]()
in unit scale, and a scale![]()
.
The mollification ![]()
of a function ![]()
by the mollifier ![]()
in the scale ![]()
is given by
![]()
(2.1)
where the mollifier ![]()
is assumed to be given by![]()
, so that![]()
. Now the
Fourier transform of ![]()
is given by
![]()
(2.2)
2.1. Evaluation of Mollifiers
Following [4] , we consider the following requirements in evaluating the mollifiers. The first two were mentioned in [3] , as Criteria 1 and 2.
Requirement 1 ![]()
is essentially zero for ![]()
higher than a threshold frequency.
If this is satisfied, noise reduction is expected, since high frequency contribution is important in noise. This is concluded from (2.2).
Requirement 2 ![]()
is nonnegative for all![]()
.
If this is satisfied, the Gibbs phenomenon does not appear.
Requirement 3 The region where ![]()
takes nonzero values is narrow.
If this is satisfied, the mollified function is less smeared.
2.2. Mollifiers Based on Wavelets
We proposed three mollifiers based on wavelets in [4] .
Mollifier 1 This mollifier is based on a special one of rapidly decaying harmonic wavelet. It is given by
![]()
(2.3)
Mollifier 2 This mollifier is based on the Haar wavelet, and is given by![]()
, where
![]()
(2.4)
Mollifier 3 This mollifier is based on the first-order-spline wavelet, which is given by
![]()
(2.5)
where
![]()
(2.6)
Here
![]()
(2.7)
![]()
for ![]()
is the ![]()
-th-order B-spline [7] . In [4] , Mollifier 3 is called the molli-
fier based on the scaled unorthogonalized Franklin wavelet, since the scaling functions of the Franklin wavelet is constructed by orthogonalizing the scaling functions of the first-order B-spline wavelet.
Remark 1 In the method of ![]()
-factor of Lanczos [8] , ![]()
, and in its extension,
![]()
[8] .
In Figures 1-3, ![]()
and ![]()
are shown in (a) and (b), respectively, for the three mollifiers.
Figure 1(a) and Figure 3(a) show that Requirement 1 is well satisfied for Mollifiers 1 and 3. Figure 2(a) shows that ![]()
does not decay rapidly as ![]()
increases for Mollifier 2, and hence Requirement 1 is not well satisfied for this mollifier.
In discussing the Gibbs phenomenon, we use function![]()
, which is given by
![]()
(2.8)
and is shown in Figures 1(c)-3(c) by thin line. In Figures 1(c)-3(c), ![]()
for ![]()
are shown by thick lines for the three mollifiers. Figure 1(b) and Figure 1(c) show that ![]()
takes small negative values, but the Gibbs phenomenon is hardly observed for Mollifier 1. We note that Requirement 2 is well satisfied for Mollifiers 2 and 3.
Mollifier 3 is so scaled that the variance of ![]()
is equal to![]()
, that is the value for Mollifier 2. The
standard deviation is then![]()
. The corresponding values for Mollifier 1 are ![]()
and![]()
.
By Requirement 3, Mollifier 1 is little less smeared.
The evaluations are summarized in Table 1.
3. Detection of Edge of a Function
Following Mathieu et al. [5] [6] , we take up the function ![]()
given by
![]()
(3.1)
This function ![]()
and its derivative ![]()
are shown in Figure 4. We note from Figure 4(b), that
![]()
(3.2)
At the point![]()
, ![]()
takes the maximum value. We take this as the place of the edge.
![]()
Table 1. Summary of the evaluations of the three mollifiers.![]()
: satisfies very well, and![]()
: satisfies fairly well.
We now consider a noisy data given by
![]()
(3.3)
for ![]()
for![]()
, where![]()
, and ![]()
for each ![]()
is a random number chosen from the uniform
distribution in the interval![]()
. In Figure 5, we show the graphs of ![]()
and ![]()
for![]()
, 0.01 and 0.1, where
![]()
(3.4)
From Figure 5(b) for very small![]()
, we can detect the point of the edge, but from Figure 5(f) for![]()
, we cannot see the existence of an edge.
We are interested in the place of an edge where the derivative of the function ![]()
is maximum, but we assume that we only know a noisy function ![]()
in place of![]()
. Then in the method of mollification, we calculate the derivative of the mollified function![]()
. If ![]()
is locally integrable, ![]()
is given by (2.1). We now know only discrete values ![]()
for![]()
, and we use
![]()
for![]()
. Since this is a differentiable function, its derivative is denoted by
![]()
.
In Figure 6, we show the curves of ![]()
and ![]()
for Mollifier 1. The values of ![]()
and ![]()
are found in the respective figures. For each![]()
, the noise is reduced as ![]()
decreases. The chosen values of ![]()
are the highest values for which the noise in ![]()
is removed fairly well. We can now point out the place at which the derivative is maximum even for the case of![]()
. In Figure 7 and Figure 8, the corresponding curves of ![]()
are shown for Mollifiers 2 and 3, respectively. The curves in Figure 8 for Mollifier 3 resemble very closely to the corresponding curves in Figure 6. The curves for ![]()
in Figure 7 for Mollifier 2 are noisier than the other figures.
In Figure 7 and Figure 8, the mollification of![]()
, that is ![]()
is drawn in place of
![]()
on the leftmost column. They are obtained by applying the mollification to the ![]()
on the second column. We note that the additional application of mollification improves the result. In fact, the following fact follows from construction of Mollifiers 2 and 3.
Remark 2 ![]()
for ![]()
in Figure 7 must be equal to ![]()
for ![]()
in Figure 8.
Since the calculation of mollification is simple for Mollifier 2, the use of ![]()
for Mollifier 2 is recom-
mended. If ![]()
is to be used, we have to use it for Mollifier 1 or 3.
![]()
Figure 5. (a), (c), (e): The curves of![]()
, and (b), (d), (f): those of![]()
.
![]()
Figure 6. The curves of ![]()
and ![]()
for Mollifier 1.
![]()
Figure 7. The curves of ![]()
and ![]()
for Mollifier 2.
![]()
Figure 8. The curves of ![]()
and ![]()
for Mollifier 3.
4. Fractional Derivatives and Primitive CRONE fD Detector
In formulating primitive CRONE fD detector, fDs are used. These are usually defined in terms of fIs.
4.1. Liouville fD and Weyl fD
In this section, we use notations ![]()
and ![]()
to represent ![]()
and
![]()
for![]()
. For![]()
, notation ![]()
is used to represent the least integer that is
not less than![]()
.
Definition 1 We define the Liouville fI and the Weyl fI of order ![]()
of a function ![]()
by
![]()
(4.1)
We define their fDs of order ![]()
of ![]()
by
![]()
(4.2)
where![]()
, and![]()
. Even when ![]()
does not exist, we put
![]()
or![]()
, if the righthand side exists [9] . We
also call ![]()
and ![]()
defined by (4.1)-(4.2) for![]()
, simply the fD as a whole.
In [5] [6] , the fDs defined by (4.1)-(4.2) for ![]()
are denoted by
![]()
(4.3)
where
![]()
When![]()
, (4.3) agrees with (4.1). When![]()
, (4.3) should be regarded as expressions of “distributions”, and be read as
![]()
(4.4)
![]()
(4.5)
where![]()
, and
![]()
(4.6)
The righthand sides are seen to be equal to the righthand sides of the corresponding equations in (4.2).
Lemma 1 Let ![]()
be such that ![]()
for all![]()
. Then
![]()
(4.7)
if the righthand side exists.
4.2. Riesz fD
In [10] , the Riesz fI is defined by
![]()
(4.8)
![]()
(4.9)
for![]()
.
Definition 2 We define the Riesz fD by (4.8) for![]()
, excluding ![]()
for![]()
.
Definition 3 We define a related fD by
![]()
(4.10)
for![]()
, excluding ![]()
for![]()
.
We note that
![]()
and the fDs defined by Definitions 2 and 3 are related by
![]()
(4.11)
![]()
(4.12)
for![]()
.
Remark 3 In [10] , ![]()
for ![]()
is called the conjugation of Riesz integral.
In [11] , ![]()
and ![]()
for ![]()
are called the Riesz potential and its
conjugate, respectively. In [12] , ![]()
for ![]()
and for ![]()
are called the Riesz potential and its inverse, respectively, and ![]()
for ![]()
and for ![]()
are called the modified Riesz potential and its inverse, respectively.
By using Lemma 1 and Definitions 2 and 3, we confirm the following lemma.
Lemma 2 Let ![]()
be such that ![]()
for all![]()
. Then
![]()
(4.13)
4.3. Primitive CRONE fD Detector in Terms of Riesz fD
Mathieu et al. [5] [6] proposed a detector of an edge which they called the CRONE detector. We call the one proposed for a function without noise as the primitive CRONE fD detector. By using (4.3), we can express it as
![]()
(4.14)
By using (4.2) and (4.8), we can express it also as
![]()
(4.15)
If![]()
, (4.15) gives![]()
.
Lemma 3 If ![]()
is an even function, ![]()
is also an even function.
Proof This follows from Lemma 2 by using (4.15).
5. Primitive CRONE fD Detector Applied to a Function without Noise
In the present section, we are concerned with the function ![]()
given by (3.1) without noise. This function ![]()
and its derivative ![]()
are shown in Figure 4.
The function ![]()
given by (3.1) is expressed as
![]()
(5.1)
Its Liouville fD of order ![]()
satisfying ![]()
is given by
![]()
(5.2)
When![]()
, this takes only finite values.
By using (4.2), Lemma 1 and (3.2), we obtain
![]()
(5.3)
For ![]()
without noise, the primitive CRONE fD detector applied to it is calculated by using (4.14), (5.2)
and (5.3). In Figure 9, we compare ![]()
for ![]()
and 0.75, with
![]()
. Here ![]()
and 0.75 are chosen as typical values between 1 and 2 and between 0 and 1.
![]()
is an even function around the point of a peak, and hence ![]()
is also an even function around
the point, as seen in Figure 9. We note that the latter has a sharper peak, for![]()
. Based on this fact,
Mathieu el al. [5] [6] claim that ![]()
for ![]()
is more favorable than ![]()
as a detector of edge.
6. Primitive CRONE fD Detector Applied to Mollified Function
In the present section, we are concerned with noisy data of the function ![]()
given in Section 3.
We now investigate the primitive CRONE fD detector applied to![]()
, and hence calculate
![]()
given by
![]()
(6.1)
for ![]()
and 0.75. This is compared with![]()
.
Numerical calculation of the righthand side of (6.1) is made by using
![]()
(6.2)
for ![]()
and![]()
, and ![]()
satisfying![]()
. Here ![]()
for![]()
. Note that (6.2) is applicable for![]()
. This equation is obtained by applying the trapezoidal rule of integration to the righthand side of the first equation of (4.12), with the aid of (4.9). In Figure 10 and Figure 11, we show the curves of
![]()
for Mollifiers 2 and 3, respectively. The curves for ![]()
are the same as in Figure 7 and Figure 8. Here we do not give the figures for Mollifier 1, since they are so close to those for Mollifier 3, shown in Figure 11. The values of ![]()
and ![]()
are found in the respective figures. In some of the figures, the curve of ![]()
is drawn but the curve of ![]()
is not drawn, that is the case when the ![]()
is too noisy to draw. On the leftmost column, ![]()
are drawn. As compared with other figures for the same ![]()
in Figures 6-8, Figure 10 and Figure 11, they are smeared and poor. On the second column, ![]()
are shown, which are obtained by applying the mollification to ![]()
given on the third column. We note that it is well mollified compared with![]()
.
The curves of ![]()
in Figure 10 for Mollifier 2 are noisier than the corresponding curves in Figure 11 for Mollifier 3. Corresponding to Remark 2, we note here the following fact.
Remark 4 ![]()
for ![]()
in Figure 10 must be equal to ![]()
for ![]()
in Figure 11.
Hence the best choice in this case is to use ![]()
for Mollifier 2, for which the mollification is very simple. If ![]()
is to be used, then we have to use it for Mollifiers 1 or 3.
7. Conclusions
The method of mollification based on wavelets is applied to the detection of the edge of a function, when the given data involve noise. Here an edge of a function is the place where the derivative of the function is maximum or minimum. In Section 3, noisy data ![]()
are given for![]()
, 0.01 and 0.1. The data and its difference ![]()
are shown in Figure 5. The primitive CRONE fD detector is given in Section 4.3.
In detecting the edge of a function, we calculate![]()
, which is the derivative of mollified
data function, and its mollification ![]()
in Section 3. In Section 6, we calculate
![]()
, which is the result of the application of the primitive CRONE fD detector to the molli-
fied data function, and its mollification![]()
. Calculations are made for three mollifiers. The
results for Mollifiers 1 and 3 are very close, and the results for Mollifier 1 are not given in Section 6. In these calculations, the results for Mollifier 2 are noisier than the others.
In Section 3. ![]()
are found to improve the results of![]()
. The curves of ![]()
for Mollifier 2 are so improved that they are very close to those for Mollifiers 1 and 3. This section is concluded as follows. Since the
calculation of mollification is simple for Mollifier 2, the use of ![]()
for Mollifier 2 is most recommended. If ![]()
is to be used, we have to use it for Mollifiers 1 or 3.
In Section 6, ![]()
is also calculated, but it is too smeared and is not useful. In Section 6, the curves of ![]()
are found to improve those of![]()
. This section is concluded as follows. The best choice in this case is to use ![]()
for Mollifier 2, for which the mollification is very simple. If ![]()
is to be used, then we have to use it for Mollifiers 1 or 3.
We finally compare the curves of ![]()
and![]()
, which are given in Sections 3 and 6, respectively. The curves of ![]()
are calculated for a larger value of ![]()
than the curves of ![]()
for the same![]()
, and hence the former have a sharper top. The general form of the curves of ![]()
is slender than that of![]()
. The calculation is simpler for ![]()
for Mollifier 2.
Acknowledgements
The authors are grateful to Professor Hiroaki Hara, who showed the recent book of Ortigueira. A preliminary report of the content of this paper was done orally by T. Morita, in a semi-plenary lecture in the 5th Symposium on Fractional Differentiation and Its Applications, held in Nanjing, China, on May 14-17, 2012. The authors are indebted to Professor Nobuyuki Shimizu, for giving the authors this opportunity.