1. Introduction
One of the fundamental issues in Wireless Sensor Networks (WSNs) is the coverage problem, which directly affects the QoS of a WSN [1] [2] . Coverage problem includes two categories, that is, radio coverage and sensing coverage [2] -[4] . Radio coverage refers to the spatial extent of effective radio propagation of a sensor node. Radio coverage directly affects the network connectivity, which is the foundational issue to ensure the normal operation of the whole network. According to the existing researches, radio coverage problem will cause cover blind area [2] -[6] , which will cause the QoS of network communication declining, packet loss rate increasing and even network partition [5] -[10] . Under the new situation of the large-scale application on WSN, strengthening the research on radio coverage of WSN has important significance for the WSNs planning, diagnosis and maintenance.
Existing researches generally adopt ideal circular emission model as a node coverage model to simplify the network coverage problem [8] -[10] ; this model ignores the signal attenuation caused by environmental factors in the process of radio propagation. However, ideal circular model is too simple and will result in great errors in practical application environment. Ideal circular model also will cause some coverage control algorithm and communication protocols failing in practical application. Plenty of studies have shown that radio coverage of sensor nodes is irregular [11] -[14] . Literature [12] established a model for the irregularity of the radio coverage of sensor nodes and gave a quantitative description for radio irregularity by using DOI (Degree of Irregularity) model; the DOI is defined as the maximum radio range variation per unit degree change in the direction of radio propagation, and this model commendably reveals RISS’s irregular continuous distribution. However, DOI model is a probabilistic model which has significant limitation in practical application. Base on the empirical data obtained from RSSI measurement, literature [13] proposed the Radio Irregularity Model (RIM) which has a better operability than the previous DOI model. However, RIM needs to collect a large number of experimental data to estimate the model parameters.
In addition, in the field of mobile communications, channel measurement method is generally adopted to determine the radio coverage of a mobile base station, and this method carries out specific channel measurement to collect RSSI drive test data and then calculates radio coverage according to the calibrated empirical model. This method has the advantage of high accuracy, but it is not well suitable for the application of large-scale densely deployed WSNs due to the high channel measurement cost.
Motivated by the problems mentioned above, this paper presents NRC-Map algorithm to estimate the radio coverage of a sensor node by its neighbor nodes. Firstly, we collect the RSSI data of the all node pairs in network. Secondly, the neighbor nodes are divided into different sectors according to their spatial location. Thirdly, the RSSI sampling values of each sector are handled by the least squares fitting, and then we can establish the log-distance path loss model for each sector. Fourthly, with the log-distance path loss model and the given signal attenuation threshold, we can calculate the maximum radio radius of each sector. Finally, the radio coverage of a sensor node can be estimated by overlapping all the sectors.
The rest of the paper is organized as follows. In Section 2, we briefly introduce the current popular wireless channel models in WSNs. In Section 3, we first present the NRC-Map algorithm. In Section 4, experiments and analysis are detailed. Finally, we conclude the paper in Section 5.
2. Wireless Channel Models
Radio irregularity is a common and non-negligible phenomenon in wireless radio systems. It arises from multiple factors which can be generally divided into two categories: devices and the propagation media. The former includes the antenna type, the sending power, antenna gains and the Signal-Noise Ratio (SNR), etc. The latter includes the media type, the background noise and some other environmental factors, such as the terrain, vegetation and obstacles, etc. Overall, radio irregularity is caused by the anisotropy of transmission media and the heterogeneous nature of device. Wireless channel models can be generally divided into theoretical models and empirical models, the models suitable for WSNs are free-space propagation model, log-normal distribution model, log-distance path loss model and Hata model. However, free-space propagation model, log-normal distribution model and Hata model are less used due to the factors of multipath, diffraction and obstructions, and extensive studies generally adopt the log-distance path loss model in practical application. When the node receives the signal, the path loss is
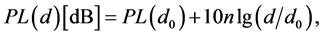 (1)
(1)
where 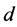 is the distance between the sending node and the receiving node,
is the distance between the sending node and the receiving node, 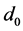 is the reference distance in meters usually adopting 1,
is the reference distance in meters usually adopting 1, 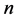 is the path attenuation factor which is sensitive to the specific environment, denotes the degree of path loss increased with the increasing distance,
is the path attenuation factor which is sensitive to the specific environment, denotes the degree of path loss increased with the increasing distance, 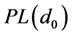 is the path loss in dB when the reference distance is
is the path loss in dB when the reference distance is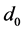 . Equation (1) can be further simplified as
. Equation (1) can be further simplified as
 (2)
(2)
where 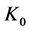 is constant
is constant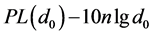 ,
, 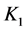 is constant
is constant . Hence, the path loss
. Hence, the path loss 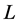 can be expressed as a function only related to T-R distance
can be expressed as a function only related to T-R distance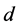 . According to the specific application environment, the major problem for the path loss modeling is to provide a set of localized calibration coefficients
. According to the specific application environment, the major problem for the path loss modeling is to provide a set of localized calibration coefficients 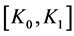 based on RSSI sampling data.
based on RSSI sampling data.
3. NRC-Map Algorithm
For precision and energy-efficiency, we present NRC-Map algorithm to estimate the radio coverage of sensor nodes through the RSSI receiving values of its neighbor nodes. The proposed algorithm is based on two basic assumptions, that is, densely deployed sensor nodes in monitoring area and the node location is known. Our algorithm is detailed as follows.
Step 1. Sensor node 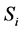 records the mean RSSI value between
records the mean RSSI value between 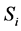 and its neighbor node
and its neighbor node![]() , and then report the triple
, and then report the triple ![]() to the sink node, where
to the sink node, where ![]() is the receiving node,
is the receiving node, ![]() is the sending node,
is the sending node, ![]() is the mean RSSI value received by
is the mean RSSI value received by![]() .
.
Step 2. Let sensor node ![]() as the origin, establish a Cartesian coordinate system. Line between sensor node
as the origin, establish a Cartesian coordinate system. Line between sensor node ![]() and all its neighbor nodes, and we can get a set of rays. Then sort the rays counterclockwise according to the increase of the angle between the ray and the positive of the x-axis, we can get the new sorted neighbor node series
and all its neighbor nodes, and we can get a set of rays. Then sort the rays counterclockwise according to the increase of the angle between the ray and the positive of the x-axis, we can get the new sorted neighbor node series![]() .
.
Step 3. As shown in Figure 1, in![]() , let the sliding window size
, let the sliding window size ![]() equals 3 and the sliding step is 1, then we can get
equals 3 and the sliding step is 1, then we can get ![]() sectors.
sectors.
Step 4. The RSSI sampling values of each sector are handled by the least squares fitting, and then we can get the log-distance path loss model for each sector. The number of the RSSI sampling values of each sector is denoted by ![]() and the actual path loss of a neighbor node sampling is denoted by
and the actual path loss of a neighbor node sampling is denoted by![]() , from Equation (2), we can calculate the predicted path loss which is denoted by
, from Equation (2), we can calculate the predicted path loss which is denoted by![]() . Due to the measurement error, there must be some differences between
. Due to the measurement error, there must be some differences between ![]() and
and![]() , we should minimize the Square Sum of Error (SSE) according to the least squares theory, so
, we should minimize the Square Sum of Error (SSE) according to the least squares theory, so
![]() (3)
(3)
Calculate the partial derivatives of ![]() and
and ![]() by Equation (3), assume that the partial derivatives equals to 0, we can get
by Equation (3), assume that the partial derivatives equals to 0, we can get
![]() (4)
(4)
Further simplify Equation (4) and we can get
![]() (5)
(5)
Thus we can get the modified parameters ![]() by solving Equation (5) and obtain the localized signal loss model parameters.
by solving Equation (5) and obtain the localized signal loss model parameters.
Step 5. For each sector, if the signal attenuation threshold MAX_LOST is given, we can obtain the maximum radio radius ![]() of each sector according to the following formula:
of each sector according to the following formula:
![]() (6)
(6)
Step 6. We can get the radio coverage of each sector according to its angle and the maximum radio radius. From the above discussions, the radio coverage of sensor node ![]() is the union of all the sectors. However, the obtained radio coverage is not continuous variation, so we line the arc roof of each sector with smooth curve and finally get the radio coverage of sensor node
is the union of all the sectors. However, the obtained radio coverage is not continuous variation, so we line the arc roof of each sector with smooth curve and finally get the radio coverage of sensor node![]() .
.
4. Experiments and Analysis
We carry out two actual experiments to verify the effectiveness of the proposed algorithm. The experiments are conducted in an open football field. Telosb node produced by Cross Bow is used in the experiments. The wireless transceiver chip of Telosb node is CC2420, and its operating frequency is 2.4 GHZ. We put each Telosb node 0.75 meters above the ground, the transmission power level of the sending node is 7 (−15 dBm), the path loss threshold MAX_LOST is 95 dB. Telosb node sent 200 packets continuously in each test period and sent one packet per 100 ms.
1) The measurement of the actual radio coverage: we aim to accurately measure the radio coverage of sensor nodes when the given maximum path loss threshold is 95 dB and use to verify the prediction results of the proposed algorithm.
2) The collection of the RSSI value: we aim to collect the RSSI data of all the node pairs in network so that we can use the proposed algorithm to estimate the radio coverage of sensor nodes.
4.1. The Measurement of the Actual Radio Coverage
The main steps involved: Node 0 was fixed as the sending node and node 1 was fixed as the receiving node. Assumed that north was the initial position, and node 1 was counterclockwise rotated 360 degrees around node 0 with 5 degrees step. We made a mark on the ray corresponding to each rotation step where the RSSI path loss measured by node 1 was 95 dB and recorded the angle of the current ray. Then, we could get the actual radio coverage of node 0 by linking all of these marks mentioned above with smooth curve.
4.2. The Collection of the RSSI Value
For the convenience of the experiments, we random tested 300 sampling positions around node 0 by using 10 data receiving nodes, and then recorded the coordinates and the average RSSI value of each sampling position. Data preprocessing involved following steps: first of all, abandoned the path loss values greater than 95 dB and we got 216 effective data. Secondly, in order to simplify the calculation, we mapped Cartesian coordinates of the sampling data to polar coordinates and sorted them according to the angular size. Finally, we randomly selected 12, 24, 36, 48, 60, 72, 84, 96, 108 and 120 sampling data from the sorted data to constitute 10 groups of the neighbor nodes set.
4.3. Further Discussion
Figure 2 shows the comparison between the coverage predicted by the proposed algorithm and the actual cov-
![]()
Figure 2. The comparison between the results predicted by the proposed algorithm and the actual coverage.
erage when the number of the neighbor nodes is 12, 48 and 72 respectively. Figures 2(a)-(c) show that the more the neighbor nodes are, the coverage predicted by the proposed algorithm is closer to the actual coverage, which fully shows the effectiveness of our proposed algorithm.
Define the coverage predicted by the proposed algorithm is![]() , and the actual coverage is
, and the actual coverage is![]() , then the area error
, then the area error ![]() is given by
is given by
![]() (7)
(7)
As shown in Figure 3, the 10 groups of the area errors between the results predicted and the actual coverage can be calculated by Equation (7). It also shows that the area error rate decreases gradually with the increase in the number of the neighbor nodes. The area error rate has a rapid decline when the number of the neighbor nodes is between 12 and 48, a relatively rapid decline between 48 and 72 and a slow decline between 72 and 120. When the number of the neighbor nodes is 12, the area error rate reaches the maximum, which can be 26.6%. This demonstrates that the proposed algorithm is sensitive to the number of the neighbor nodes. The fewer number of the neighbor nodes is, the greater prediction error gets. When the number of the neighbor nodes is between 60 and 72, the area error rate is less than 10%, which indicates that the proposed algorithm has the performance of ideal prediction. When the number of the neighbor nodes is 120, the area error rate can reach the minimum, which is only 6.8%. Due to the number of the neighbor nodes is enough at this moment, the predicted coverage is very close to the actual coverage. However, due to the complexity of radio propagation, the proposed algorithm can’t accurately predict the actual radio coverage of sensor nodes.
5. Conclusions
Radio irregularity is a non-negligible phenomenon in wireless radio system. DOI model and RIM model quantitatively describe radio irregularity, and reveal that the RSSI path loss is irregular and continuous distribution. However, this kind of model needs to be corrected by collecting a large amount of experimental data in specific application environment. Therefore, it has much limitation in practical application. This paper presents NRC- Map algorithm to estimate the radio coverage of sensor nodes through RSSI values collected by the neighbor nodes. That is, the neighbor nodes are divided into different sectors according to their spatial position. Then the RSSI sampling values of each sector are handled by the least squares fitting. Base on the sampling values, we establish the log-distance path loss model for each sector. Then, we get the maximum radio radius of each sector by the path loss model and the given signal attenuation threshold. The radio coverage of sensor nodes can be estimated by overlapping all the sectors.
![]()
Figure 3. The area error predicted by the proposed algorithm.
Experimental results indicate that the proposed algorithm is simple and practicable, and this algorithm does not require specific experiments to verify its feasibility. This algorithm can fully approximate to the actual radio coverage of sensor nodes under the condition of a certain number of neighbor nodes. This algorithm effectively improves the prediction accuracy of the radio coverage of sensor nodes.
The algorithm proposed in this paper has better effect especially in the application of densely deployed WSNs. Moreover, the prediction results are of great practical value and application flexibility on the diagnosis and maintenance of WSNs. However, the prediction accuracy of the proposed algorithm is relatively low in sparsely deployed sensor networks. Thus, the future work of our research will focus on how to improve the prediction accuracy of the algorithm in sparsely deployed sensor networks.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (No. 41101426 and No. 61364023), the Natural Science Foundation of Jiangxi Province (No. CA201204330) and the Science Research Project of Jiangxi Education Department (No. GJJ12429).