1. Introduction
An optimal power flow (OPF) consists of solving equations which characterize an electrical power system (active and reactive power of each node) adjusting the control variables values (voltages or powers) in order to optimize a specific system parameter, represented by one target function [1] . A system usually includes state variables (unknown quantities) and independent variables (unknown data). Control variables can be any of the independent variables in the system, and are selected depending on the purpose of the analysis.
The target function of a power system for the OPF study is determined depending on the parameter which is going to be optimized or improved; some typical parameters are as follows [2] :
· Minimizing the generation cost
· Minimizing transmission losses of active power
· Minimizing transmission losses of reactive power
· Minimizing the interruption costs by flows
· Minimizing the reprogramming number of controls
· Minimizing pollutant emissions of thermal generators
In order to improve the features of power systems and reduce line losses, in recent years, the electrical microgrids have appeared. Electrical microgrids are small electrical systems that may have autonomous management of power generation and energy distribution, which can function in a dependent or independent way from the electrical grid and also with the potential implementation of renewable energy sources [3] .
To enhance features and achieve an optimal performance in electrical microgrids, authors as [4] - [8] have implemented OPF in various mathematical algorithms.
This paper presents a state of art regarding the mathematical methods which have been implemented in the analysis of OPF and its application in electrical microgrids. Subsequently, a mathematical algorithm based on the gradient method is proposed for the solution of OPF in low power microgrids, in order to improve the profiles voltages and consequently reduce the active power losses. Finally, the application results of the gradient method in a low power microgrid with photovoltaic generation are presented.
2. State of Art
An OPF solution provides information regarding to planning, economic programming, system control and the distribution of future expansion [9] . Sections 2.1 and 2.2 present a compilation of the most relevant research on OPF analysis methods in power systems and its application in electrical microgrids.
2.1. Optimal Power Flow Methods
These mathematical methods have been developed for over 40 years, starting with classical mathematical optimization techniques [9] - [11] , and more recently reaching genetic and artificial intelligence algorithms [4] [6] [9] [12] [13] . OPF mathematical methods are shown in Figure 1 and Figure 2.
This section presents the most important contributions in OPF methods.
![]()
Figure 1. OPF methods (Classic optimization).
In the year of 1968 H. W. Dommel and W. F. Tinney introduced the concept of OPF in power systems. The Authors present a solution method for OPF using the Newton method with an optimal adjustment of the control parameters through the gradient method; this is done with the purpose of reducing losses of a three-node system [10] .
In 1973 A. M. H. Rashed and D. H. Kelly presented a mathematical algorithm to minimize losses implementing a combination of Lagrange multipliers and Newton’s method, replacing the Jacobian for one Hessian matrix. The proposed method has a faster convergence, requiring fewer steps compared to other methods [14] .
In 1993 Yu-Chi Wu, et al. introduced a method to resolve OPF in order to optimize an economic dispatch. The study combines an algorithm based on the interior point method, justifying that the methods proposed years ago did not meet the requirements of large-scale power systems. The authors concluded that the method provided robust and accurate results [15] .
Subsequently, in 1995 J. Kennedy and R. Eberhart conducted a research in optimization of nonlinear functions using the “Particle Swarm Optimization” (PSO) method. Thus, the authors state that this method could be used to solve a myriad of problems, including the OPF in power systems [12] .
In the year of 2001 C.A. Roa-Sepúlveda and B.J. Pavez-Lazo introduced an OPF method to resolve the economic dispatch problem based on linear Programming. This method is applied to tow IEEE systems of six and thirty nodes without considering the losses; finally, they concluded that OPFs could be solved without a Jacobian matrix, contributing to determine any objective function [7] .
In 2004 A. EL-Dib, et al. focused their research in an application (PSO) to figure out OPF as optimization problems. The authors argue that these studies are the basis to determine the voltage stability and the maximum system power [13] .
In 2006 R. Mageshvaran, et al. presented three different techniques to solve OPF (PSO, CPSO, HDE), proposing useful and encouraging solutions, that were verified in Matlab. The objective of the research was the development of new techniques that allow a better operation; this was done with the purpose of ensuring an economic generation and also meeting the demand of active and reactive power through simple and efficient algorithms [9] .
In the year of 2008 J. M. LópezLezema and L. A. GallegoPareja developed an algorithm to solve OPF, employing the gradient method for achieving reduction of active power losses in power systems. In their research the authors reduced the quantity of iterations by means of the adjustment parable method [11] .
In 2012 C. H. Fujisawa, et al. concentrated their research on direct current OPF with losses and into alternating current; they further presented the mathematical characteristics of each one and their respective advantages and disadvantages. The authors determined that the alternating current method is the most interesting model, since it solves problems through an iterative process and applying various methods of linear programming [16] .
In Section 2.2 are exposed OPF applications in power systems, specifically in electrical microgrids.
2.2. Optimal Power Flow Applied to Electrical Microgrids
The implementation of OPF in electrical microgrids started years ago at first, to control the optimal power dispatch [8] [11] and subsequently to achieve the loss minimization in power systems [4] [5] .
In 2009 E. Sortomme and M. A. El-Sharkawi conducted studies in a microgrid through the Particle Swarm Optimization (PSO); this was done in order to achieve an optimal dispatch of controllable loads and effectively use the storage energy devices that microgrids contain. The authors emphasized that the research was a preliminary study where they concluded that peak loads were reduced in 10 MV, generating an economic improvement of 14% [8] .
In the year 2010 P. Wan and M. D. Lemmon considered an optimization algorithm for distributed event to solve OPF in microgrids. The optimization was performed by simulations in Sim Power System (Matlab) implementing the microgrid model: CERTS. In this study the authors reduced the error by the algorithm and conclude that through the method the optimization problem in microgrids could be solved [6] .
In 2013 E. Dall’Anese, et al. applied several OPF to electrical microgrids in order to minimize losses and the cost of the energy supplied by distributed generation (small energy sources capable of supplying user demand), this was done by SDR techniques (Semidefinite Programming), which the possibility of obtaining the optimal solution for the microgrid [5] .
In 2013 Yoash Levron, Josep M. Guerrero and Yuval Beck introduced a solution for OPF that considered a microgrid with energy storage. The authors claim that classical solutions of OPF were not adapted for the microgrid analysis, in particular due to the presence of distributed generation and of the storage devices. The Optimal Power Flow developed by authors considered the limitations of the storage devices and those of the microgrid regarding to the voltages, currents and powers [4] .
3. Algorithm Based on the Gradient Method
In order to analyze electrical microgrids by OPF, a mathematical algorithm is proposed based on the gradient method, based upon the study developed in [10] . Figure 3 shows the proposed flowchart of an OPF solved by the gradient method.
The mathematical algorithm is based on partial derivatives and has the property to be modified to analyze any structure in the microgrid (isolated or interconnected with the grid).
In Section 3.1 the general way of formulating an OPF is shown. Afterwards, in Section 3.2 the specific methodology proposed for the formulation and solution of an OPF is explained, which is based on the gradient method with the purpose of improving the voltage profiles and reducing active power losses in electrical microgrids.
![]()
Figure 3. Flow diagram of an OPF based on the gradient method.
3.1. Obtaining the Probability Density Functions
According to [10] , the OPF is based on Equation (1).
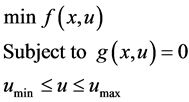 (1)
(1)
where (x) are state variables and (u) control variables [17] :
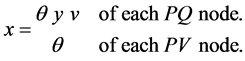
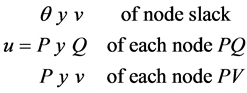
The control variables can be adjusted without altering the equality and inequality. Therefore, the problem of OPF is to adjust the control variables u in order to optimize a specific parameter of the system represented by the objective function f(x, u) [10] .
The equality restrictions g(x, u) of Equation (1), correspond to the active and reactive power of the system nodes equations:
 (2)
(2)
Finally, the inequality restrictions are the minimum and maximum allowed values for the control variables.
3.2. Gradient Method for Improving the Voltage Profiles and Reducing Active Power Losses in a Microgrid
Improving the voltage profiles and reducing losses in the microgrid helps to improve performance, to enhance the useful life of the conductors, to improve energy quality and reduce system costs [18] .
Control variables are defined as generation nodes voltages and Slack as it look for improving the system voltages profiles.
In a power system, slack power node is not specified, because the node assumes the losses of the system [6] . Consequently, the microgrid losses are minimized when the powers of the nodes are kept constant and when the power generation of the Slack is minimized.
According to the previous idea, function f(x, u) is going to be the Slack node power of the microgrid. Equality restrictions g(x, u) of Equation (1) will be the typical power equations which define each node in a power system [19] :
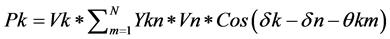 (3)
(3)
 (4)
(4)
The inequality restrictions (5) are the minimum and maximumvoltages allowed on themicrogrid. Considering that the proposed OPF is particularly for low voltage microgrids and also that for the Colombian case, this levels are 120/208 with limits of +5% (126) y −10% (108) [20] :
 (5)
(5)
Finally, Equation (6) represents the formulation of an OPF to improve the voltage profiles and reduce the active power losses in a low voltage electrical microgrid.
 (6)
(6)
where

3.3. Mathematical Algorithm for OPF Based on the Gradient Method for an Electrical Microgrid
In [10] , they are based on an equation named Lagrangian (7) to solve OPF, which has a Lagrange multiplier λ.
 (7)
(7)
If minimun necessary conditions or Karush Kunh-Tucker conditions are applied to Equation (7) [11] , the systems of Equations (8), (9) and (10) are obtained. Optimal microgrid solution is determined by solving the equations system.
 (8)
(8)
 (9)
(9)
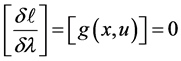 (10)
(10)
The gradient in (9) measures the sensitivity of the objective function with regard to the changes in control variables. Originating at an opposite direction to the gradient, a minimum feasible point with a lower function value is reached [11] . Repeating this process leads to the optimal solution of a system.
The new control values are updated by (11) to continue the iterations until the error will reduce to a minimum.
![]() (11)
(11)
In Equation (11), the variable is the value that determines the step size that should result from the algorithmin the opposite directionto the gradient. If a low value for c is chosen, a convergence is ensured, however it makes that a lot of iterations be necessary. Instead, if a high value for c is chosen, it will produce oscillations around the optimum [10] .
4. Case of Study
4.1. Electrical Microgrid Proposed
Figure 4 shows the proposed microgrid for the case of study. This system is proposed for its simplicity and the presence of an unconventional generator. The microgrid has a power of 800 w, which is fed by the main grid and a photovoltaic generator, which to a specific temperature and irradiance generates 450 w (interconnected microgrid).
In order to illustrate the improvements in the system with the OPF, Figure 5 shows the losses of active power before (13.1589) and after (11.7640) the application of the algorithm.
4.2. Application of the Algorithm and Results
The mathematical algorithm of the proposed OPF was developed in Matlab, selecting different values for the
![]()
Figure 4. Microgrid for the case of study.
![]()
Figure 5. Microgrid losses before and after the OPF implementation.
step size (c = 0.1, c = 0.3 and c = 1.38) with an error tolerance of 0.0001 (ε = 0.0001).
The mathematical algorithm minimizes the difference between the power generated by the grid and the photovoltaic panel, so that losses are minimized. The results show that there is a range of values that minimizes microgrid losses, which is shown in (12). This occurs because the rate of change of the voltage decreases each iteration, until the point where a change in the control variables exerts a change in the power of the Slack node.
![]() (12)
(12)
The results with different step sizes were the following (Table 1):
As shown in Table 1, the number of iterations required to reach the optimum of the system depends on the size of step (c) chosen. Selecting a value c = 0.1 the algorithm meets the limit of error in 22 iterations; however, if this value increases to 0.3, iterations will be reduced to 8. If the step size increases highly (c = 1.38), the algorithm will present a premature convergence with only 4 iterations generating oscillations.
4.3. Voltage Profiles and Active Power Losses
In order to verify the obtained results in the microgrid, an analysis of profile voltages and system losses was realized by means of power flows through the Newton-Raphson method in Power System Analysis Toolbox (PSAT) by Matlab. The results are represented by Figure 6 and Figure 7.
To examine the voltage profiles in the microgrid, power flows for different cases which can be present in the system were realized, considering the limits in Equation (8), subsequently comparing graphically with the optimal values found with the OPF.
The cases mentioned above are shown in Table 2. The voltage profiles of the microgrid are illustrated in
![]()
Table 1. Results with different step sizes.
![]()
Figure 7. Microgrid active power losses.
![]()
Table 2. Case of study for voltage profiles in the microgrid.
Figure 7. In this figure, the flattening of the curve (black straight) with the optimal voltage values determined by the OPF can be observed (Case 25).
The analysis of losses was performed in the same way that the voltage profiles, executing various power flows for cases described on Table 2 and comparing with the resulting values of the OPF. As Figure 7 shows, the losses decrease when the optimal voltages are applied (V1 = 121.1844 v and V2 = 118.5517) compared to normal operating conditions (V1 = 120 v and V2 = 120 v). The black dot indicates the maximum reduction of system losses.
5. Conclusions
The state of art concerning the OPF and its application in microgrids, reveals that despite of the significant development in this field, the studies developed in microgrids (isolated or interconnected) with photovoltaic generation has not been investigated in a substantial way.
An OPF can improve parameters in microgrids as voltage profiles and thus the active power losses. These factors take a leading role in the efficiency, quality, and reliability of an electric system.
Due to the ability to change of the proposed OPF, this method can be applied to low voltage electrical microgrids. In addition, the implemented mathematical algorithm has a lower complexity, compared to methods based on genetic and artificial intelligence algorithms.
The proposed algorithm reduces the active power losses and improves the voltage profiles with a minimal error. Additionally, the method ensures the convergence, which can be improved by modifying the step size c of the algorithm.
By changing the equation of the objective function, the proposed method can optimize or improve any parameter into an electrical microgrid considering that math is the same for all conditions.