Fuzzy Logic for Solving an Optimal Control Problem of Hypoxemic Hypoxia Tissue Blood Carbon Dioxide Exchange during Physical Activity ()
1. Introduction
Hypoxia, or hypoxiation, is a pathological condition related to adequate oxygen supply in human body. The derived adequate oxygen supply can be whole body (generalized hypoxia) or its region (tissue hypoxia). Generalized hypoxia occurs in healthy people when they ascend to high altitude, where it causes altitude sickness leading to potentially fatal complications: high altitude pulmonary edema (HAPE) and high altitude cerebral edema (HACE) [1] . Hypoxia also occurs in healthy individuals when breathing mixtures of gases with a low oxygen content that is while diving underwater especially when using closed-circuit re-breather systems that control the amount of oxygen in the supplied air. A mild and non-damaging intermittent hypoxia is used intentionally during altitude training to develop an athletic performance adaptation at both the systemic and cellular level.
Hypoxia is also a serious consequence of preterm birth in the neonate. The main cause for this is that the lungs of the human fetus are among the last organs to develop during pregnancy. To assist the lungs to distribute oxygenated blood throughout the body, infants at risk of hypoxia are often placed inside an incubator capable of providing continuous positive airway pressure (also known as a humidicrib).
Hypoxia denotes oxygen deficiency at the mitochondrial sites due to insufficient delivery of oxygen (low ) or inability to use oxygen (normal
) or inability to use oxygen (normal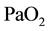 ). Hypotonic hypoxia is characterized by a
). Hypotonic hypoxia is characterized by a 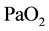 less than
less than 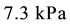
 . Below this threshold, the ventilation starts to increase by carotid body activity. Acute hypoxia with low
. Below this threshold, the ventilation starts to increase by carotid body activity. Acute hypoxia with low 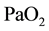 stimulates the carotid bodies. This triggers a rise in ventilation (primary hyperventilation). The hyperventilation reduces
stimulates the carotid bodies. This triggers a rise in ventilation (primary hyperventilation). The hyperventilation reduces 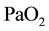 and
and , which limits the initial rise in ventilation, because it decreases the carotid body and central chemoreceptor stimuli.
, which limits the initial rise in ventilation, because it decreases the carotid body and central chemoreceptor stimuli.
In humans, hypoxia is detected by chemoreceptors in the carotid body. This response does not control ventilation rate at normal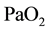 , but below normal the activity of neurons innervating these receptors increases dramatically, so much so to override the signals from central chemoreceptors in the hypothalamus, increasing
, but below normal the activity of neurons innervating these receptors increases dramatically, so much so to override the signals from central chemoreceptors in the hypothalamus, increasing 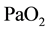 despite a falling
despite a falling 
Any physical activity will obviously cause the body to demand more oxygen for normal functioning. The muscles will rob the brain of the marginal amounts of oxygen available in the blood and the time of onset of hypoxic symptoms is shortened.
This paper is organized as follows. Section 2 presents the model equations and optimal control problem. A short description of strategy approach by fuzzy logic for solving optimal control problems is discussed in this section. Section 3 is interested in the application of the direct approach and the approach integrating the fuzzy logic for solving an optimal control problem of glucose-insulin in diabetic human. The numerical simulation is presented in Section 4. Finally, we present conclusion remarks in Section 5.
2. Methods
First of all we focus on the models equations as developed by Guillermo Gutierrez [2] . The diagram for a two compartmental model is illustrated in the Figure 1 where mass transport model of tissue  exchange is developed to examine the relative contributions of blood flow and cellular hypoxia (dysoxia) to increases in tissue and venous blood
exchange is developed to examine the relative contributions of blood flow and cellular hypoxia (dysoxia) to increases in tissue and venous blood  concentration.
concentration.
From the diagram presented in the Figure 1, the equations of the model can be formulated as follows.
![]() (1)
(1)
![]() (2)
(2)
where the variable states ![]() and
and ![]() are function of time we prefer to denote also t.
are function of time we prefer to denote also t.
It is known that the human respiratory control system varies the ventilation rate ![]() in response to the levels of
in response to the levels of ![]() and
and ![]() in the body and the control mechanisms of cardiovascular system influences global control in the blood vessels as well as heart rate
in the body and the control mechanisms of cardiovascular system influences global control in the blood vessels as well as heart rate ![]() for changing blood flow
for changing blood flow ![]() [3] . Generally, during physical activity in altitude and particular in the hypoxia case, the control mechanism of these two system plays a crucial role.
[3] . Generally, during physical activity in altitude and particular in the hypoxia case, the control mechanism of these two system plays a crucial role.
Consequently, the control of cardiovascular and respiratory system is described via the following two ordinary differential equations respectively.
![]() (3)
(3)
![]() (4)
(4)
where the functions ![]() and
and ![]() are determined by an optimality criterion.
are determined by an optimality criterion.
Now let be interested in writing the arterial blood ![]() and
and![]() . First of all the venous concentration of
. First of all the venous concentration of ![]() in the vascular compartment is calculated from Fick’s equation that allows to determine the rate at which oxygen is being used during physical activity as
in the vascular compartment is calculated from Fick’s equation that allows to determine the rate at which oxygen is being used during physical activity as
![]()
where ![]() is arterial concentration of
is arterial concentration of ![]() and
and ![]() denotes the production of
denotes the production of ![]() Therefore the venous oxyhemoglobin saturation
Therefore the venous oxyhemoglobin saturation ![]() is calculated from
is calculated from ![]() by neglecting the contribution of dissolved
by neglecting the contribution of dissolved ![]() as follows
as follows
![]()
where ![]() is the blood hemoglobin concentration in
is the blood hemoglobin concentration in ![]()
By considering the calculation done in [2] , the arterial pressure of ![]() [4] is
[4] is
![]() (5)
(5)
where ![]() is taken as constant
is taken as constant ![]() and
and
![]()
Similarly, blood ![]() is calculated on the basis of the Henderson-Hasselbach equation [5]
is calculated on the basis of the Henderson-Hasselbach equation [5]
![]() (6)
(6)
where ![]() is
is ![]() content of plasma defined by Douglas [6] as follows
content of plasma defined by Douglas [6] as follows
![]()
The respiratory control system aims at keeping ![]() and
and ![]() closely to their equilibrium values
closely to their equilibrium values![]() and
and ![]() respectively. Furthermore, the cost functional can be formulated in the following way.
respectively. Furthermore, the cost functional can be formulated in the following way.
Find ![]() and
and ![]() solution of
solution of
![]() (7)
(7)
subject to the system (1)-(2) and (3)-(4).
In the relation (7), the positive scalar coefficients![]() ,
, ![]() ,
, ![]() and
and ![]() determine how much weight is attached to each cost component term in the integrand while
determine how much weight is attached to each cost component term in the integrand while ![]() denotes the maximum time that the physical activity can take.
denotes the maximum time that the physical activity can take.
Let us consider ![]() the vector space that is span of a base of linear B-splines functions
the vector space that is span of a base of linear B-splines functions
![]() (8)
(8)
on a regular grid
![]() (9)
(9)
The functions![]() ,
, ![]() verify the following relation
verify the following relation
![]()
where ![]() denotes Kronecker symbol. The discretisation of the optimal problem (7) is done by setting the state vector
denotes Kronecker symbol. The discretisation of the optimal problem (7) is done by setting the state vector
![]()
and the desired final vector
![]()
such that it can be written as follows.
![]() (10)
(10)
where
![]()
with![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() respectively the
respectively the ![]() component of the vectors
component of the vectors![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() .
.
We are looking for ![]() an approximated solution of (10) in the set
an approximated solution of (10) in the set ![]() such that
such that
![]() (11)
(11)
Therefore the cost function (10) becomes
![]() (12)
(12)
where (12) is determined using rectangular method such that the discretisation is done on a regular grid![]() .
.
Finally, the discrete formulation of optimal problem (7) subject to (1)-(2) and (3)-(4) is written as follows.
![]() (13)
(13)
where ![]() is a matrix
is a matrix ![]() such that
such that ![]() are components of the function
are components of the function ![]() in the set
in the set ![]() and
and ![]() represents the matrix with
represents the matrix with ![]() component is
component is ![]() where
where ![]() denotes the two first
denotes the two first
components of solution of the system (1)-(2) and (3)-(4) associated to![]() ,
, ![]() and
and ![]() are matrix defined by
are matrix defined by
![]() (14)
(14)
Description of Fuzzy Logic Strategy Approach
Let us consider the following problem.
Find![]() ,
, ![]() that minimizes
that minimizes
![]() (15)
(15)
subject to
![]() (16)
(16)
where ![]() and
and ![]() are positive defined matrices.
are positive defined matrices.
The problems (15) and (16) can be solved by the dynamic programming method. This method has a fast convergence, its convergence rate is quadratic and the optimal solution is often represented as a state of control feedback [7] . However, the solution determined by this method depends on the choice of the initial trajectory and in some cases this solution is not optimal. It is for this reason that the integration of the fuzzy logic [8] can permit to determine quickly the optimal solution. We develop a linearization strategy of the subject system by an approach based on the fuzzy logic. This approach had been developed by Takagi-Sugeno [9] [10] . The model that has been introduced in 1985 by Takagi-Sugeno permits to get some fuzzy linearization regions in the state space [11] . While taking these fuzzy regions as basis, non linear system is decomposed in a structure multi models which is composed of several independent linear models [12] . The linearization is made around an operating point contained in these regions.
Let’s consider the set of operating point ![]()
![]() . Different fuzzy approximations of the nonlinear term
. Different fuzzy approximations of the nonlinear term ![]() can be considered.
can be considered.
The approximation of order zero gives:
![]() (17)
(17)
Using the first order of Taylor expansion series we obtain:
![]() (18)
(18)
To improve this approximation, we introduce the factor of the consequence for fuzzy Takagi-Sugeno system. This factor permits to minimize the error between the non linear function and the fuzzy approximation. If ![]() designates this factor, the approximation (18) can be formulated as the following form:
designates this factor, the approximation (18) can be formulated as the following form:
![]() (19)
(19)
If one replaces the term ![]() by its value approached in (16), the linearization around
by its value approached in (16), the linearization around ![]() leads to
leads to
![]() (20)
(20)
where ![]() and
and ![]() are square matrix which has
are square matrix which has ![]() order and
order and ![]() matrix with
matrix with ![]() order.
order.
Therefore, the optimal control problems (15) and (16) become a linear quadratic problem which the feedback control is given by the following expression [13] [14] :
![]() (21)
(21)
where
![]() (22)
(22)
is the feedback gain matrix and ![]() discreet Riccati equation solution of the following form
discreet Riccati equation solution of the following form
![]() (23)
(23)
It is obvious that the linearization around every operating point gives the system for which the equations have the form (20). Because there are ![]() operating points, we have
operating points, we have ![]() systems which have this form. Therefore, according to the relation (21)
systems which have this form. Therefore, according to the relation (21) ![]() controls are determined. The defuzzyfication method [10] permits to determine only one system and only one control
controls are determined. The defuzzyfication method [10] permits to determine only one system and only one control![]() .
.
Then, this transformation gives the following equation:
![]() (24)
(24)
![]() (25)
(25)
where
![]() (26)
(26)
and where ![]() designates membership degree partner to the operating point
designates membership degree partner to the operating point![]() .
.
3. Numerical Approaches for Solving the Optimal Control Problem (7), (1)-(4)
3.1. Fuzzy Strategy
To approximate the optimal control problems (7), (1)-(2) and (3)-(4), we propose to use the explicit Euler scheme. The stability of this scheme constitutes an advantage to approach some ordinary differential equations.
The discretisation of the constraints (1)-(2) and (3)-(4) is done using the first order explicit Euler method. From the Equations (1)-(2) and (3)-(4) and taking ![]() and
and ![]() we have the following system
we have the following system
![]() (27)
(27)
Applying the first order explicit Euler’s method, the system (27) is transformed as follow
![]() (28)
(28)
where ![]() Taking
Taking ![]() as operating point and assuming
as operating point and assuming ![]() as oper-
as oper-
ating point number related to each operating point we have the system
![]() (29)
(29)
where
![]()
Let us set the following variable change
![]() (30)
(30)
that is
![]()
The system (27) can be formulated using the relations (6) and (30) but here we prefer to keep this form. The use of these relations is taken into account in numerical simulation. Therefore, the approximation of objective function (7) is made using the rectangular method and it becomes
![]() (31)
(31)
where
![]()
and where![]() ,
, ![]() and
and ![]() are the same as taken in subsection 2.1. Finally, the optimal control problems (7), (1)-(2) and (3)-(4) becomes the following a linear quadratic (LQ) problem.
are the same as taken in subsection 2.1. Finally, the optimal control problems (7), (1)-(2) and (3)-(4) becomes the following a linear quadratic (LQ) problem.
Find ![]() solution of
solution of
![]()
subject to
![]()
3.2. Direct Approach
To approximate the system (1)-(4), let us consider
![]() (32)
(32)
a linear B-splines basis functions on the uniform grid
![]() (33)
(33)
such that
![]()
Let us introduce the vector space ![]() whose the basis is
whose the basis is ![]() We have
We have
1) ![]()
2) ![]()
Let us consider ![]() and let us take the interpolation operator
and let us take the interpolation operator
![]()
satisfying
![]() (34)
(34)
We verify easily that
![]() (35)
(35)
![]() . (36)
. (36)
Therefore, the system (1)-(4) can be approached by the following form
Find ![]() solution of the system
solution of the system
![]() (37)
(37)
![]() (38)
(38)
![]() (39)
(39)
![]() (40)
(40)
![]() (41)
(41)
such that
![]() (42)
(42)
![]() (43)
(43)
![]() (44)
(44)
![]() (45)
(45)
To approximate the optimal problems (1)-(4), let us set![]() the state vector,
the state vector, ![]() the initial state vector,
the initial state vector, ![]() the equilibrium state vector
the equilibrium state vector ![]() the wanted equilibrium vector,
the wanted equilibrium vector, ![]() the control vector;
the control vector;![]() ,
, ![]() ,
,
![]() , designate the
, designate the ![]() components of the vector
components of the vector ![]() and
and ![]() and
and ![]() denote
denote ![]() components of the vector
components of the vector ![]() and
and ![]()
Therefore, the problems (1) and (2) can take the following compact form
![]() (46)
(46)
where ![]() is solution of the approximated solutions (37)-(41).
is solution of the approximated solutions (37)-(41).
We must determine ![]() an approximate solution of (46) in
an approximate solution of (46) in ![]() It is necessary to note that we can write
It is necessary to note that we can write
![]() (47)
(47)
Therefore, we can approximate the objective function by
![]() (48)
(48)
where![]() . The convergence of the discreet objective function (48) toward the continuous objective func-
. The convergence of the discreet objective function (48) toward the continuous objective func-
tion given by the problem (46) has been shown in [15] .
Finally, the optimal control problems (7), (1)-(2) and (3)-(4) are minimisation problems with constraint. The discreet formulation of such problem can be written as follows.
Find ![]() solution of
solution of
![]() (49)
(49)
subject to
![]() (50)
(50)
where ![]() is a matrix
is a matrix ![]() such that the components
such that the components ![]() are those function
are those function ![]() in
in ![]() and
and ![]() is
is
the matrix such that the ![]() component is
component is ![]() where
where ![]() is the solution of (50) associated to
is the solution of (50) associated to![]() .
.
4. Numerical Simulation
Let us consider a hypoxic patient (a 30 year old woman) practicing jogging as physical activity for a period of ![]() minutes. The values of determinant parameters of a 30 years old woman in this physical activity are given in [15] . Setting up
minutes. The values of determinant parameters of a 30 years old woman in this physical activity are given in [15] . Setting up ![]() we have
we have![]() . We consider a universe of discourse
. We consider a universe of discourse ![]() which has four linguistic variables: tissue total
which has four linguistic variables: tissue total ![]() concentration
concentration![]() , vascular total
, vascular total ![]() concentration
concentration
![]() , heart rate
, heart rate ![]() and ventilation rate
and ventilation rate![]() . According to the physiology of cardiovascular-respiratory system, we consider
. According to the physiology of cardiovascular-respiratory system, we consider![]() ,
, ![]() ,
, ![]() and
and ![]() Then we
Then we
take ![]() min (minimum tissue total
min (minimum tissue total ![]() concentration),
concentration), ![]() tmiddle (middle tissue total
tmiddle (middle tissue total ![]() concentration) and
concentration) and ![]() max (maximum tissue total
max (maximum tissue total ![]() concentration) of the linguistic variable
concentration) of the linguistic variable![]() . In an analogous way,
. In an analogous way, ![]() min,
min, ![]() middle and
middle and ![]() max (respectively Hmin, Hmiddle and Hmax;
max (respectively Hmin, Hmiddle and Hmax; ![]() min,
min, ![]() middle and
middle and ![]() max) are the terms of the variable linguistic
max) are the terms of the variable linguistic ![]() (respectively
(respectively ![]() and
and![]() ). During the physical activity, tissue total
). During the physical activity, tissue total ![]() concentration (respectively vascular total
concentration (respectively vascular total ![]() concentration, heart rate and ventilation rate) vary such that we can consider a universe of discourse
concentration, heart rate and ventilation rate) vary such that we can consider a universe of discourse ![]() where the labels are centered at 25, 30 and 35 (respectively
where the labels are centered at 25, 30 and 35 (respectively![]() ,
, ![]() and
and ![]()
![]() ,
, ![]() and
and ![]() and
and ![]()
![]() and
and![]() ). It is obvious that these points take the corresponding values in the labels centers of a universe of discourse
). It is obvious that these points take the corresponding values in the labels centers of a universe of discourse ![]() [8] .
[8] .
The operating points associated to those linguistic variables are given in the Table 1, membership functions associated to this labeling are represented in the Figure 2 and Figure 3 and Table 2 shows the obtained degrees of membership of each linguistic variable.
Using parameters values from Table 3 we get ![]() and
and ![]() and the following matrices
and the following matrices
![]()
![]()
Table 1. Variables and their operating points.
![]()
Table 2. Variables and their corresponding degrees of membership.
The next step of the fuzzy logic strategy at this point is the defuzzification. The formulas used in the defuzzification are illustrated in (26). Now considering our Equation (29), the matrices ![]() and
and ![]() remain unchanged. However, as matrices
remain unchanged. However, as matrices ![]() and
and ![]() contain a variable
contain a variable![]() , calculation is made after replacing
, calculation is made after replacing ![]() with its operating points presented in Table 1. With parameters from Table 3, we get
with its operating points presented in Table 1. With parameters from Table 3, we get
![]()
Since there are three linear state systems, the solution leads to three feedback controls of the form
![]()
where ![]() is a gain feedback. The implementation can be made in several platforms. Here we use MATLAB package where we use the built-in function dare for solving discrete Riccati Equation (23) if
is a gain feedback. The implementation can be made in several platforms. Here we use MATLAB package where we use the built-in function dare for solving discrete Riccati Equation (23) if ![]()
![]()
![]() . After calculation, we obtain
. After calculation, we obtain
![]()
For solving the optimal control problem (7) subject to the system (1)-(2) and (3)-(4), we take ![]() and
and ![]() The numerical simulation gives the graphical results. The Figure 4 illustrates both the variation of the heart rate and ventilation rate. Figure 5 presents the impact of physical activity due to two controls of cardiovascular-respiratory system in the variation of tissue and vascular carbon dioxide while Figure 6 shows the responses of the partial pressure of carbon dioxide and oxygen.
The numerical simulation gives the graphical results. The Figure 4 illustrates both the variation of the heart rate and ventilation rate. Figure 5 presents the impact of physical activity due to two controls of cardiovascular-respiratory system in the variation of tissue and vascular carbon dioxide while Figure 6 shows the responses of the partial pressure of carbon dioxide and oxygen.
![]() (a) (b)
(a) (b)
Figure 4. Variation of heart rate (a) and Ventilation rate (b) for a 30 years old woman during jogging as her physical activity. The curves in dotted line represent the parameter for the direct approach. The curve dashed line show the parameter for the approach integrating the fuzzy logic strategy.
![]() (a) (b)
(a) (b)
Figure 5. Variation of carbon dioxide in tissue (a) and in vascular (b) for a 30 years old woman during jogging as her physical activity. The curves in dotted line represent the parameter for the the direct approach. The curve dashed line show the parameter for the approach integrating the fuzzy logic strategy.
![]() (a) (b)
(a) (b)
Figure 6. Variation of optimal arterial partial pressure of carbon dioxide (a) and oxygen (b) for a 30 years old woman during jogging as her physical activity. The curve in solid line represents the wanted value. The curve in dotted line indicates the optimal parameter for the approach integrating the fuzzy logic strategy. The curve in dashed line represents the optimal parameter for the direct approach.
The controls variation of the cardiovascular respiratory system are represented in Figure 4 which shows the increase of both the heart rate and the alveolar ventilation until they reach a stabilized state. It is a perfect representation of the importance of physical activity in the regulation of the cardiovascular respiratory system; in order to avoid or even heal non severe Hypoxemic-Hypoxia. In the case of Hypoxemic-Hypoxia, there is a perfect deficit of oxygen in the body. The ventilation rate plays an important role in the gas supply and regulation through the body. An increase in heart rate and ventilation rate results in an adequate and regular supply of both oxygen and carbon dioxide in the body. The Figure 5 shows a decrease of tissue and venous carbon dioxide concentration. This results from the brut increase of ventilation during the initial stage of the physical activity which is followed by a gradual increase of ventilation. The absence of a perfect ventilation leads to an increase (decrease) of carbon dioxide ![]() and oxygen
and oxygen ![]() resulting from an accumulation of lactic acid. For a 30 years old woman during jogging as her physical activity, the Figure 6 shows the arterial partial pressure of carbon dioxide (resp. oxygen) decreases (resp. increases) in the time of physical activity until the stabilization at normal value. The results obtained in this work are rather satisfactory. In particular, the reaction of the cardiovascular and respiratory system to physical activity can be modeled and a feedback can be approximated by the solution of a linear quadratic problem. Physical activity reduces the risk of Hypoxemic-Hypoxia or contacting any cardiovascular-respiratory disease. Physical activity induces important changes in the stabilization of cardiac, vascular and blood
resulting from an accumulation of lactic acid. For a 30 years old woman during jogging as her physical activity, the Figure 6 shows the arterial partial pressure of carbon dioxide (resp. oxygen) decreases (resp. increases) in the time of physical activity until the stabilization at normal value. The results obtained in this work are rather satisfactory. In particular, the reaction of the cardiovascular and respiratory system to physical activity can be modeled and a feedback can be approximated by the solution of a linear quadratic problem. Physical activity reduces the risk of Hypoxemic-Hypoxia or contacting any cardiovascular-respiratory disease. Physical activity induces important changes in the stabilization of cardiac, vascular and blood
5. Concluding Remarks
In this work, two numerical approaches have been compared to determine the optimal trajectories of arterial pressures of of carbon dioxide and oxygen as response to controls of cardiovascular-respiratory system subjected to a physical activity. The finding results show that those two used methods are satisfactory and closed. Consequently, the approach integrating the fuzzy logic strategy is very important for the resolution of the optimal control problem. In particular, it gives the optimal trajectories of cardiovascular-respiratory system in the same way it ensures their performance.
NOTES
*Corresponding author.