1. Introduction
There are many and various concepts about the nature of changes to light when the source moves relatively to the receiver. I all shall not list and analyze them; here I shall just state the understanding to which I have come.
Numerous experiments have established that light is electromagnetic action of one body on another. The nature of light influence is the same, as well as a nature of action of transmitting aerial of a radiation source on the reception aerial of a radio receiver.
In the elementary transmitting aerial, in the flat condenser, the charged particle tests the action directed perpendicularly to plates. If the power supply is connected to the condenser with a variable voltage the force of action on this particle will change, remaining perpendicular to the plates. Such action on the charged particle will exist outside of the condenser, but its value will decrease with distance. This variable electric action is named as electromagnetic waves. If between plates there will be a magnetized body the variable force of action on one of its poles will be directed perpendicularly to the force acting on the charged body, and also is perpendicular to a direction of removal from the condenser. Therefore, at any point in space near the average plane of the condenser, on the charged particle placed in it, or on a magnetic pole, there will be the action that is directed perpendicular to the direction of this point from the condenser. Therefore the elementary waves are called “transverse”.
The receiver of this electromagnetic action might be the charged particle or the magnetic pole, if it were possible to measure their transverse fluctuations. But the development of radio engineering went another way. The receiver of variable electromagnetic influence is the similar condenser, on whose plates there is a variable electric charge that is transformed to an alternating current. This current is amplified, and that information which was transferred by the receiver is thus restored.
The electromagnetic influence of light differs from electromagnetic influence of radio waves by the much greater frequency. Numerous experiments have established that the physical properties of electromagnetic action essentially depend on the value of frequency. Apparently, this appreciably applies to light. There is a line of its properties that for other electromagnetic waves are not shown. However there is the uniform electromagnetic nature of light and radio waves concerning the action of a moving electromagnetic source on the receiver. In particular, there are identical laws for change of characteristics of electromagnetic action from a source with its movement relative to the receiver.
2. Laws of Electromagnetic Interaction for Two Objects with Relative Motion
It is well known that, upon movement of a magnet relative to a condenser, on its plates there appears an electric charge. Therefore, if to place between plates of the condenser the charged particle there will be a mechanical action on it from a moving magnet, i.e. the particle will get movement. If the condenser plates to close a conductor, the current will run in the conductor. This effect is identical to a case when the magnet moves relatively the coil with a conductor. At short circuit of its ends the current will be in the conductor. The value of a current does not depend on whether the coil or the magnet moves. The strength of the current is determined from the velocity of their relative movement. As is known [1] , this phenomenon is described by Faraday’s law induction.
A similar situation arises with movement of an electrified body. Its movement relative to a magnet is identical to a current, and the current creates mechanical action on the magnet pole; i.e., the moving charge creates a mechanical influence on the magnet. This influence is described in [1] using the experimental Biot-Savart-Laplace’s law for the current element. The interaction of the moving charged body and the magnet also does not depend on whether the charged body or the magnet moves. It depends on the velocity of their relative movement. If the charge and the magnet move relative to a third body, for example Earth’s surface, but with respect to each other they rest, in this case the charge and the magnet do not interact. In this case, the coil does not interact with the magnet.
The variable electromagnetic interaction between the source and the receiver (in modern terminology, electromagnetic waves) is defined by the first and second of Maxwell’s equations. In turn, these equations are another form of record of two experimental laws [1] : Faraday’s law induction, and Biot-Savart-Laplace’s law. Excluding the magnetic intensity H from Maxwell’s equations, we receive D’Alembert’s equation for electric intensity E
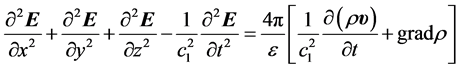 , (1)
, (1)
where 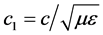 is the speed of light in the considered media;
is the speed of light in the considered media; 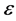 is dielectric permittivity of media;
is dielectric permittivity of media;  is magnetic permeability of media;
is magnetic permeability of media;  is the density of electric charges distributed in the space of the x, y, z coordinate system; v is the velocity of charges. Equation (1) defines the force of influence of moving charges on a motionless point particle of which the charge is equal to unity. And the movement with velocities v occurs relative to the motionless particle.
is the density of electric charges distributed in the space of the x, y, z coordinate system; v is the velocity of charges. Equation (1) defines the force of influence of moving charges on a motionless point particle of which the charge is equal to unity. And the movement with velocities v occurs relative to the motionless particle.
We have solved D’Alembert’s Equation (1) for the action of one point charged particle on another when the first moves relative to the second with velocity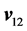 . Also we have received expression for force:
. Also we have received expression for force:
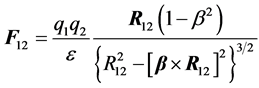 , (2)
, (2)
where 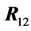 is the radius-vector from the first charge to the second;
is the radius-vector from the first charge to the second; 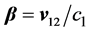 is the normalized velocity.
is the normalized velocity.
The force (2) depends on relative velocity of movement v, and at 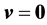 it passes to Coulomb’s law:
it passes to Coulomb’s law:
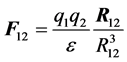 , (3)
, (3)
which, as is known, determines force of interaction of two motionless charges.
So, all electromagnetic experiments and results (1)-(2), which follow from them, testify that laws of electromagnetic interaction of two objects depend on their relative velocity. From here two important conclusions follow. The first one testifies an inaccuracy of the principle of relativity, when it applies to interaction of objects moving from each other. In this case we may not tell that Laws of a Nature (for example, Coulomb’s law (3)) do not depend on movement of an object. On the contrary, the law of electromagnetic interaction of two objects (2) depends on their relative movement. So, the principle of relativity, which used in the Theory of Relativity (TR), is incorrect. The second conclusion testifies to absence of the world medium: the luminiferous medium, ether, the medium of physical vacuum, etc. It follows that the electromagnetic interaction of two objects depends on their relative velocity, and does not depend on absolute velocity relatively to the imagined world medium.
3. Laws Describing Electromagnetic Waves
The variable electromagnetic action (in the accepted terminology: electromagnetic waves, electromagnetic radiation, light, etc.) of a source on the receiver depends on their relative velocity. This dependence (Doppler effect, phenomenon of aberration) for a long time was established from astronomer’s observations. However for their theoretical explanation, various models of propagation of light were involved. As we see, all these models are speculative. The real dependence of light influence of a source on a receiver with their relative movement may be established only on the basis of experimental laws of electromagnetism, which are received as a result of measurement of mechanical interactions.
In case of variable electromagnetic action the constant charge is absent, and its density ; therefore, at equality to zero of the right part of D’Alembert’s equation, Equation (1) becomes the wave equation
; therefore, at equality to zero of the right part of D’Alembert’s equation, Equation (1) becomes the wave equation
 . (4)
. (4)
As shown in our works, for example [2] [3] , the partial case of its solution is the equation of a plane wave
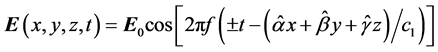 , (5)
, (5)
where E0 = const is amplitude; f is frequency of fluctuations; 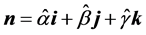 is a normal to the plane of the wave; the direction cosines with x, y, z coordinate axes are:
is a normal to the plane of the wave; the direction cosines with x, y, z coordinate axes are:
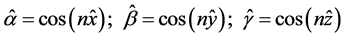 .
.
4. Interaction of the Source and the Receiver with Their Relative Motion
Expression (5) describes change of electric intensity E at any point of the x, y, z coordinate system, and at any moment in time. This change is caused by a variable electromagnetic source. From the formula (5) follows, that the changes of E in space are propagated with speed c1. If an electromagnetic source is a point source, far from it Equation (5) will describe its influence at little changes of distance. And for the exact description of its action it is necessary to use the solution of the wave Equation (4) for a spherical wave [2] [3] . The receiver, which is placed in a point with coordinates x, y, z according to expression (4), will test variable action of the source.
In case of movement of a source, for example, with velocity v in the direction of the x axis, its influence on the receiver already will be another. So to calculate it, it is necessary to make change of electromagnetic characteristics of a source, which it is caused by its movement relatively the receiver. In works [2] [3] we have gone in another way. We have asked the question: under what conditions will expression (2) for force of interaction the relatively moving charged particles coincide with Coulomb’s law (3) for force of interaction of the motionless charged particles? It is obvious, that for this purpose it is necessary the values which are included in expression (3) to express through values on which depends (2). Appeared, that exists two variants of transformations of expression (3) to expression (2). We shall use one of them. Thus the parameters interaction of relatively moving charges, we shall write down with the symbol “v”:
![]() (6)
(6)
Here we used the electric intensity created by the first charge, by which the force of its action on the second charge is written as![]() .
.
So, after transformation of parameters of Coulomb’s law (3) by expressions (6) it turns to expression (2) for force of interaction relatively moving charges. A similar way, having substituted in the wave equation (5) transformations (6), we shall receive expression for influence of a moving variable source with velocity v on the receiver in the following form:
![]() . (7)
. (7)
It is obvious that Equation (7) we results in the equation of a plane wave
![]() , (8)
, (8)
by assistance of expressions for frequency and directing cosines of the wave front of a moving source in the following view:
![]() , (9)
, (9)
![]() , (10)
, (10)
![]() , (11)
, (11)
![]() . (12)
. (12)
Note that for direction cosines, it is easy to verify that![]() .
.
5. Doppler Effect and Aberration of Light
We shall consider the change of frequency of light at movement of a source. Let the source comes nearer along the x axis with the normalized velocity ![]() to the receiver, which is ahead of the receiver. In this case the normal of wave front with an axis x has a zero angle:
to the receiver, which is ahead of the receiver. In this case the normal of wave front with an axis x has a zero angle:![]() , i.e.
, i.e.![]() . At small velocity of the source motion, in expression (9) it is possible to neglect the value
. At small velocity of the source motion, in expression (9) it is possible to neglect the value ![]() in comparison with 1, and the source frequency will be defined by the formula
in comparison with 1, and the source frequency will be defined by the formula
![]() . (13)
. (13)
This coincides with the formula of the classical Doppler effect. With source movement toward the receiver, the frequency of light will increase. And with retreat of the source from the receiver![]() , the frequency of light will decrease. However, with velocity of the source or of the receiver with a velocity comparable to speed of light, a more precise formula for change of frequency of light from the source is necessary for defining under the formula (9). At velocity v comparable to speed of light
, the frequency of light will decrease. However, with velocity of the source or of the receiver with a velocity comparable to speed of light, a more precise formula for change of frequency of light from the source is necessary for defining under the formula (9). At velocity v comparable to speed of light![]() , the change of frequency of a source will essentially differ from the value determined by Doppler effect (13).
, the change of frequency of a source will essentially differ from the value determined by Doppler effect (13).
We shall consider the change of the direction of light wave front at source movement, i.e. the aberration of light (see Figure 1). Let the source (S) move along the x axis, and let the receiver (R) be in the x, y plane. So that the designations coincide with accepted ones in astronomy, we shall replace angles between the normal of wave front
![]()
Figure 1. Change of light direction at the movement of source S. S is a moving light source, which is observed by receiver R; S' is a motionless light source, which is observed by the receiver R.
of a moving source S: ![]() and of a motionless source
and of a motionless source![]() :
:![]() . Then expression (10) for change of the light wave front at the source or with the movement of the receiver will be written down as:
. Then expression (10) for change of the light wave front at the source or with the movement of the receiver will be written down as:
![]() . (14)
. (14)
Let us designate (see Figure 1) the difference of angles of normal to fronts of light waves of motionless and moving sources a symbol![]() , which is referred to as the angle of light aberration. From Figure 1, it is clear that
, which is referred to as the angle of light aberration. From Figure 1, it is clear that
![]() . (15)
. (15)
Let us find an expression for the aberration angle. With this purpose we shall find ![]() from the formula (14):
from the formula (14):
![]() (16)
(16)
Let us substitute ![]() from (15) into (16), and transform cosine
from (15) into (16), and transform cosine
![]() . (17)
. (17)
As in astronomy, the aberration angle, which takes into account orbital movement of the Earth, is used. Therefore it is very small (about 20²) and it is possible to accept in (17) that![]() . Therefore from (17) it is found that:
. Therefore from (17) it is found that:
![]() . (18)
. (18)
At small normalized velocities ![]() of the source movement, it is possible to neglect the second term in the denominator. Then the angle of an aberration will be defined by the formula:
of the source movement, it is possible to neglect the second term in the denominator. Then the angle of an aberration will be defined by the formula:
![]() . (19)
. (19)
In astronomy, this formula gives the annual movement of stars that is caused by the Earth orbital movement around of the Sun.
In recent decades, the astronomers have found objects that move with velocities that are comparable to the speed of light. The formula (19) will be incorrect for them. The changes of their angle of the light wave front direction need to be calculated under the formula (10), or, in other designations, under the formula (14).
6. Conclusions
1) Light is electromagnetic influence of the source on the receiver.
2) The electromagnetic action of one body on another depends on the velocity of their relative movement. This action does not depend on velocity of movement of the receiver or of the source from any imagined media.
3) There is no luminiferous media (an ether, a field, the media of physical vacuum etc.), with respect to which the relative movement of the source or of the receiver would change the source action on the receiver.
4) The change of frequency of light and its direction with the source movement relative to the receiver is completely determined by laws of electromagnetism.
Acknowledgements
I thank Dr. Cynthia Kolb Whitney for correcting English in paper and useful advice on its improvement.