1. Introduction
The Kauffman bracket polynomial was introduced by L. H. Kauffman in 1987 [1] in concern with link invariants. The bracket polynomial soon became popular due to its connections with the Jones polynomial, dichromatic polynomial, and the Potts model. While the HOMPLY polynomial and the bracket polynomial are distinct with different topological properties, there is a very beautiful relationship between them due to F. Jaeger [2] , and it is also observed in a special case by Reshetikhin [3] .
The Kauffman bracket (polynomial) is actually not a link invariant because it is not invariant under the first Reidemeister move. However, it has many applications and it can be extended to a popular link invariant, the Jones polynomial. In the present work we shall confine ourselves to the Kauffman bracket to avoid this work from unnecessary length and to leave it for applications.
This paper is organized as follows: In Section 2 we shall give the basic ideas about knots, braids, and the Kauffman bracket. In Section 3 we shall present the main results.
2. Basic Notions
2.1. Links
A link is a disjoint union of circles embedded in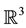 . A one-component link is called a knot. Links are usually studied via projecting them on a plan; a projection with extra information of overcrossing and undercrossing is called the link diagram.
. A one-component link is called a knot. Links are usually studied via projecting them on a plan; a projection with extra information of overcrossing and undercrossing is called the link diagram.

Two links are isotopic if and only if one of them can be transformed to the other by a diffeomorphism of the ambient space onto itself. A fundamental result by Reidemeister [4] about the isotopic link diagrams is: Two unoriented links 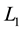 and
and 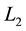 are equivalent if and only if a diagram of
are equivalent if and only if a diagram of 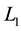 can be transformed into a diagram of
can be transformed into a diagram of 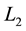 by a finite sequence of ambient isotopies of the plane and the local (Reidemeister) moves of the following three types:
by a finite sequence of ambient isotopies of the plane and the local (Reidemeister) moves of the following three types:
The set of all links that are equivalent to a link  is called a class of
is called a class of . By a link
. By a link 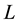 we shall always mean the class of
we shall always mean the class of![]() .
.
The main question of knot theory is Which two links are equivalent and which are not? To address this question one needs a knot invariant, a function that gives one value on all links that belong to a single class and gives different values (but not always) on knots that belong to different classes. The present work is basically concerned with this question.
2.2. Braids
Braids were first studied by Emil Artin in 1925 [5] [6] , which now play an important role in knot theory, see [7] -[9] for detail.
An n-strand ![]() is a set of
is a set of ![]() non intersecting smooth paths connecting
non intersecting smooth paths connecting ![]() points on a horizontal plane to
points on a horizontal plane to ![]() points exactly below them on another horizontal plane in an arbitrary order. The smooth paths are called strands of the braid.
points exactly below them on another horizontal plane in an arbitrary order. The smooth paths are called strands of the braid.
![]()
The product ![]() of two n-strand braids is defined by putting the braid
of two n-strand braids is defined by putting the braid ![]() above the braid
above the braid ![]() and then gluing their common end points.
and then gluing their common end points.
A braid with only one crossing is called elementary braid. The ith elementary braid ![]() on
on ![]() strands is:
strands is:
![]()
A useful property of elementary braids is that every braid can be written as a product of elementary braids. For instance, the above 2-strand braid is![]() .
.
The closure of a braid ![]() is the link
is the link ![]() obtained by connecting the lower ends of
obtained by connecting the lower ends of ![]() with the corresponding upper ends.
with the corresponding upper ends.
![]()
An important result by Alexander [10] connecting knots and braids is: Each link can be represented as the closure of a braid. This result motivated knot theorists to study braids to solve problems of knot theory.
Remark 2.1 In the last section, all the concerned links will be closures of products of elementary braids.
2.3. The Kauffman Bracket
Before the definition it is better to understand the two types of splitting of a crossing, the A-type and the B-type splittings:
![]()
In the following, the symbols ![]() and
and ![]() represent respectively the unknot and the disconnected sum.
represent respectively the unknot and the disconnected sum.
Definition 2.2 The Kauffman bracket is the function ![]() defined by the axioms:
defined by the axioms:
![]()
![]()
![]()
Here![]() ,
, ![]() , and
, and ![]() are three links which are isotopic everywhere except at one crossing where the look as in the figure:
are three links which are isotopic everywhere except at one crossing where the look as in the figure:
![]()
Proposition 2.3 The Kauffman polynomial is invariant under second and third Reidemeister moves but not under the first Reidemeister move [11] .
3. Main Results
In this section we shall introduce a recursive relation for the Kauffman bracket, shall give an explicit formula of
![]() , and shall express
, and shall express ![]() as the product of
as the product of ![]() and
and![]() .
.
First of all we give the Kauffman bracket of the ![]() -twist unknot
-twist unknot![]() :
:
![]()
Lemma 3.1 The Kauffman bracket of the ![]() -twist unknot is
-twist unknot is
![]()
Proof. We prove it by induction on![]() :
:
The case ![]() holds by definition as
holds by definition as ![]() is the unknot without any crossings. Now, with the assumption that the result holds for an arbitrary
is the unknot without any crossings. Now, with the assumption that the result holds for an arbitrary![]() , we have
, we have
![]()
Theorem 3.2 (A recursive relation) The following relation holds for any ![]()
![]() (3.1)
(3.1)
Proof. We prove it using directly the definition and Lemma 3.1:
![]()
From this recursive relation, we get the explicit formula for the 2-strand braid link![]() :
:
Proposition 3.3 The Kauffman bracket of the link ![]() is
is
![]()
Proof. We prove it by induction on![]() .
.
For![]() , we have
, we have
![]()
which satisfies the recursive relation.
With the assumption that the relation holds for an arbitrary n, we, using Theorem 3.2, get
![]()
This completes the proof. ,
In the following we give the Kauffman bracket polynomial of the closure of the braid ![]() (n factors); this sequence contains the powers of the Garside element
(n factors); this sequence contains the powers of the Garside element![]() :
:![]() .
.
Proposition 3.4 The Kauffman bracket of ![]() satisfy the recurrence relations:
satisfy the recurrence relations:
![]()
![]()
![]()
![]()
![]()
![]()
Proof. Simply, apply the definition for different values of![]() , and write recursively each next bracket in terms of the previous one. ,
, and write recursively each next bracket in terms of the previous one. ,
Lemma 3.5 The Kauffman brackets for ![]() are:
are:
![]()
![]()
![]()
![]()
![]()
![]()
Proof. The proofs of first three cases are given (proofs of remaining cases are similar):
![]()
Theorem 3.6 For any ![]() the Kauffman bracket of
the Kauffman bracket of ![]() is given by:
is given by:
![]()
Proof. We prove it by induction on![]() . The case
. The case ![]() is covered by Lemma 3.5, and the inductive step can be checked with Proposition 3.4.
is covered by Lemma 3.5, and the inductive step can be checked with Proposition 3.4.
For instance,
![]()
In connected sum ![]() of the braid link
of the braid link ![]() with the trivial knot
with the trivial knot ![]() has the diagram:
has the diagram:
![]()
Lemma 3.7
![]()
Proof. We prove it by induction on![]() :
:
For![]() , we have
, we have
![]()
Now, with the assumption that the result holds for an arbitrary![]() , we have
, we have
![]()
as required. ,
The following result confirms that the Kauffman bracket of ![]() is actually the product
is actually the product ![]()
Theorem 3.8 For any![]() ,
,
![]()
Proof. We prove it by induction on![]() :
:
When![]() ,
,
![]() (3.2)
(3.2)
Suppose the result holds for![]() , that is
, that is ![]()
Now, using Lemma 3.7, we have
![]()
This completes the proof. ,
Corollary 3.9
![]()
Proof. It is obvious: ![]()
Corollary 3.10
![]()
and
![]()
Proof. The result follows immediately from Theorem 3.8 as ![]() and span
and span ![]() ,
,
For the following, let us fix the notation ![]() for the link with the understanding that the link contains a, b,
for the link with the understanding that the link contains a, b,
and ![]() crossings of type
crossings of type![]() , and
, and![]() , respectively, and that
, respectively, and that![]() .
.
![]()
Proposition 3.11 The Kauffman bracket of the link ![]() is
is
![]()
Proof. We prove it by induction on![]() :
:
For![]() , we have
, we have
![]()
Now, with the assumption that the result holds for an arbitrary![]() , we have
, we have ![]()
![]()
![]()
as required. ,
Proposition 3.12 The Kauffman bracket of the link ![]() is
is
![]()
Proof. We prove it by induction on![]() :
:
For![]() , we have
, we have
![]()
Now, with the assumption that the result holds for![]() , we have
, we have
![]()
![]()
as was required. ,