Local Empirical Likelihood Diagnosis of Varying Coefficient Density-Ratio Models Based on Case-Control Data ()
1. Introduction
Varying coefficient models are often used as extensions of classical linear models (e.g. Shumway [1] ). Their appeals are that the modeling bias can be significantly reduced and the “curse of dimensionality” can also be avoided. These models have gained considerable attention due to their various applications in many areas, such as biomedical study, finance, econometrics, and environmental study. The estimation for the coefficient functions has been extensively discussed in the literatures, including the smoothing spline method (see Hastie and Tibshirani [2] ), the locally weighted polynomial method (see Hoover et al. [3] ), the two-step estimation procedure (see Fan and Zhang [4] ), and the basis function approximations (see Huang et al. [5] ).
In this paper, we consider the following general two-sample varying-coefficient density-ratio model
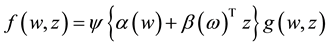 (1)
(1)
where 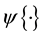 is a nonnegative known function that makes
is a nonnegative known function that makes  to be a density function, which includes the exponential-tilt model as a special case with
to be a density function, which includes the exponential-tilt model as a special case with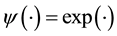 . In parametric situation, Thomas [6] and Lustbader
. In parametric situation, Thomas [6] and Lustbader
et al. [7] considered a general relative risk model, a mixture model, 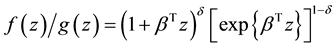 ,
,
where  is a scalar parameter that describes the general shape of the relative risk function. It includes additive relative risk model
is a scalar parameter that describes the general shape of the relative risk function. It includes additive relative risk model 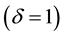 and log-linear relative model
and log-linear relative model 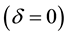 as special cases.
as special cases.
Various density-ratio models for some conventional density functions were discussed in Kay and Little [8] . It has been shown recently that the density-ratio model provides a good fit to the observed data in some medical applications (Qin and Zhang [9] ; Qin et al. [10] ; Zhang [11] ), genetic quantitative trait loci analysis (Zou et al. [12] ), and clinical trials with skewed outcomes (White and Thompson [13] ). Liu, Jiang and Zhou [14] considered estimation and inference for the two-sample varying-coefficient density-ratio model (1) by constructing the local empirical likelihood function. The EL approach is appealing for analyzing the varying-coefficient density-ratio model because the two density functions in (1) can be modeled nonparametrically. This nonparametric method of inference has sampling properties similar to the bootstrap. Another advantage of the EL approach is that it takes auxiliary information, such as the density-ratio in (1), into account to improve estimation.
The empirical likelihood method origins from Thomas & Grunkemeier [15] . Owen [16] first proposed the definition of empirical likelihood and expounded the system info of empirical likelihood. Zhu and Ibrahim [17] utilized this method for statistical diagnostic. Liugen Xue and Lixing Zhu [18] summarized the application of this method.
Over the last several decades, the diagnosis and influence analysis of linear regression model has been fully developed (R.D. Cook and S. Weisberg [19] , Bocheng Wei, Gobin Lu & Jianqing Shi [20] ). Regarding the varying coefficient model, especially for the B-spline estimation of parameter, diagnosis and influence analysis have some results (Z. Cai, J. Fan, R. Li [21] , J. Fan, W. Zhang [22] ). So far the statistical diagnostics of varying- coefficient density-ratio models with case-control data based on local empirical likelihood method has not yet seen in the literature. This paper attempts to study it.
The remainder of the article is organized as follows. Local empirical likelihood and estimation equation are presented in Section 2. The main results are given in Section 3. An example is given to illustrate our results in Section 4.
2. Local Empirical Likelihood and Estimation Equation
Let 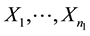 be a sequence of independent and identically distributed random vectors from the control group, each with density
be a sequence of independent and identically distributed random vectors from the control group, each with density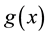 , and
, and 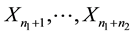 be a sequence of independent and identically distributed random vectors from the case group, each with density
be a sequence of independent and identically distributed random vectors from the case group, each with density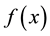 ,
, 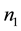 and
and 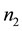 are the number of subjects in the control
are the number of subjects in the control
group and case group, respectively. Let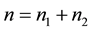 , and
, and 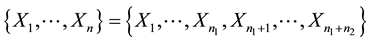 denote
denote
the pooled sample. Assume that ![]() as
as![]() . From model (1), the empirical likelihood function derived according to Prentice and Pyke [23] is:
. From model (1), the empirical likelihood function derived according to Prentice and Pyke [23] is:
![]() (2)
(2)
where![]() ,
, ![]() and
and ![]() is the distribution func-
is the distribution func-
tion corresponding to![]() . However,
. However, ![]() can not be used directly to obtain estimates for
can not be used directly to obtain estimates for ![]() and
and ![]() because
because ![]() and
and ![]() are infinite-dimensional parameters. Thus, instead of (2), we consider the localized conditional empirical likelihood below.
are infinite-dimensional parameters. Thus, instead of (2), we consider the localized conditional empirical likelihood below.
Assume that all components of ![]() and
and ![]() are smooth so that they admit Taylors series expansions, i.e., for each given
are smooth so that they admit Taylors series expansions, i.e., for each given ![]() and for
and for ![]() around
around![]() ,
,
![]() (3)
(3)
Let![]() , and
, and![]() . For simplicity,
. For simplicity,
denote ![]() by
by ![]() and
and ![]() by
by ![]() for fixed
for fixed![]() . Then, the local log empirical likelihood (LEL) function
. Then, the local log empirical likelihood (LEL) function ![]() of is
of is
![]()
where ![]() is the weight with kernel function
is the weight with kernel function ![]() and
and ![]()
represents the size of the local neighborhood. The kernel weight is used to give smoother weight to data with ![]() near
near![]() . The last constraint is the auxiliary information for the EL estimation. By the method of Lagrange multipliers, similar to that used in Owen (2001), we obtain
. The last constraint is the auxiliary information for the EL estimation. By the method of Lagrange multipliers, similar to that used in Owen (2001), we obtain
![]()
where ![]() is determined by the constraint equation
is determined by the constraint equation
![]() .
.
Motivated by Zhu and Ibrahim (2008), we regard ![]() and
and ![]() as independent variables and define
as independent variables and define
![]() .
.
Obviously, the maximum empirical likelihood estimates ![]() and
and ![]() are the solutions of following equations:
are the solutions of following equations:
![]()
3. Local Influence Analysis of Model
We consider the local influence method for a case-weight perturbation![]() , for which the empirical log-likelihood function
, for which the empirical log-likelihood function ![]() is defined by
is defined by![]() . In this case,
. In this case, ![]() , defined to be an
, defined to be an ![]() vector with all elements equal to 1, represents no perturbation to the empirical likelihood, because
vector with all elements equal to 1, represents no perturbation to the empirical likelihood, because![]() . Thus, the empirical likelihood displacement is defined as
. Thus, the empirical likelihood displacement is defined as![]() , where
, where ![]() is the maximum empirical likelihood estimator of
is the maximum empirical likelihood estimator of ![]() based on
based on![]() . Let
. Let ![]() with
with ![]() and
and![]() , where
, where ![]() is a direction in
is a direction in![]() . Thus, the normal curvature of the influence graph
. Thus, the normal curvature of the influence graph ![]() is given by
is given by![]() , where
, where
![]() ,
,
in which ![]() is a
is a ![]() matrix with
matrix with ![]() -th element given by
-th element given by![]() .
.
We consider two local influence measures based on the normal curvature ![]() as follows. Let
as follows. Let
![]() be the ordered eigenvalues of the matrix
be the ordered eigenvalues of the matrix ![]() and let
and let
![]() be the associated orthonormal basis, that is,
be the associated orthonormal basis, that is,![]() . Thus, the spectral decomposition of
. Thus, the spectral decomposition of ![]() is given by
is given by
![]() .
.
The most popular local influence measures include![]() , which corresponds the largest eigenvalue
, which corresponds the largest eigenvalue![]() , as well
, as well
as![]() , where
, where ![]() is an
is an ![]() vector with
vector with ![]() -th component 1 and 0 otherwise. The
-th component 1 and 0 otherwise. The ![]() represents
represents
the most influential perturbation to the empirical likelihood function, whereas the ![]() -th observation with a large
-th observation with a large ![]() can be regarded as influential.
can be regarded as influential.
As the discuss of Zhu et al. (2008), for varying-coefficient density-ratio model, we can deduce that
![]() (4)
(4)
where ![]()
![]()
4. Numerical StudyWe generate
We generate![]() and
and ![]() from two densities
from two densities ![]() and
and![]() , respectively. We setboth densities
, respectively. We setboth densities ![]() and
and ![]() to be trivariate normal distributions, in which
to be trivariate normal distributions, in which![]() ,
, ![]() is a scalar,
is a scalar,![]() , and
, and![]()
are trivariate normal densities with means ![]() and
and![]() , and inverses of the covariances
, and inverses of the covariances
![]()
Because![]() , we have
, we have
![]() ,
, ![]() and
and![]() .
.
We draw 1000 data sets with sample size ![]() for various values of
for various values of![]() . We
. We
choose the Epanechnikov kernel ![]() to localize the coefficient functions.
to localize the coefficient functions.
In order to checkout the validity of our proposed methodology, we change the value of the first, 125th, 374th,
789th and 999th data. For every case, it is easy to obtain![]() . For
. For ![]() and
and![]() , using the sam-
, using the sam-
ples, we evaluated their maximum empirical likelihood estimators.
Consequently, it is easy to calculate the value of ![]() and
and![]() . The result of
. The result of ![]() is as following Figure 1.
is as following Figure 1.
It can be seen from the result of ![]() that the first, 125th, 374th, 789th and 999th data are strong influence points. Indeed, our results are illustrated.
that the first, 125th, 374th, 789th and 999th data are strong influence points. Indeed, our results are illustrated.
5. Discussion
In this paper, we considered the statistical diagnosis for varying-coefficient density-ratio model based on local empirical likelihood. Through simulation study, we illustrate that our proposed method can work fairly well.