A New Scheme for Discrete HJB Equations

Zhanyong Zou

School of Mathematics and Statistics, Guangdong University of Finance & Economics, Guangzhou, China.

DOI: 10.4236/am.2014.517252                

Abstract

In this paper we propose a relaxation scheme for solving discrete HJB equations based on scheme II [1] of Lions and Mercier. The convergence of the new scheme has been established. Numerical example shows that the scheme is efficient.

Keywords

Iterative Algorithm, Relaxation Scheme, HJB Equation, Convergence, Existence

1. Introduction

Consider the following Hamilton-Jacobi-Bellman (HJB) equation:

(1.1)

where 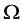is a bounded domain in are elliptic operators of second order. Equation (1.1) is arising in stochastic control problems. See [2] and the references therein.

Equation (1.1) can be discretized by finite difference method or finite element method. See [1] [3] and the references therein. Then we obtain the following discrete HJB equation:

(1.2)

where. Equation (1.2) is a system of nonsmooth nonlinear equations. Many numerical algorithms for solving (1.2) have been proposed. See [4] -[12] and the references therein.

[1] has given two iterative algorithms for solving (1.2). At each iteration, a linear complementarity subproblem or a linear equation system subproblem is solved. See also [4] .

Scheme I.

Step 1: Given for some we find such that

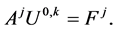
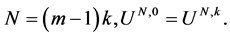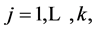Step 2: Let For we find 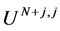such that

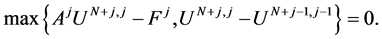
Step 3: If 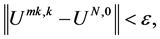then the output is 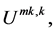otherwise 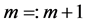and it goes to Step 2.

Assume Let

(1.3)

That is: the lth row of matrix is the lth row of matrix; the lth component of vector is the lth component of vector. Now we formulate Scheme II of Lions and Mercier in the notation above.

Scheme II.

Step 1: for some we find such that

(1.4)

Step 2: For we find such that

(1.5)

Step 3: Compute as the solution of

(1.6)

Step 4: If then the output is, otherwise and it goes to Step 2.

In the last decade many numerical schemes have been given for solving (1.2). But the above schemes are still playing a very important role. See [4] -[6] and the references therein.

In this paper we propose, based on Scheme II above, a relaxation scheme with a parameter, which for is just Scheme II. In our numerical example, the new scheme with is faster than Scheme II. The monotone convergence of the new scheme has been proved.

2. New Scheme and Convergence

We propose a new scheme which is an extension of Scheme II.

New Scheme II.

Step 1: Given for some find such that

(2.1)

Step 2: For find such that

(2.2)

Step 3: Compute as the solution of

(2.3)

Step 4: Compute

(2.4)

Step 5: If then output otherwise and go to Step 2.

In [13] we proposed the following conditions for (1.2).

Condition All the matrices are M-matrices.

In [13] we have proved the following theorem.

Theorem 2.1 If Condition holds then (1.2) has a unique solution.

We have the following convergence theorem.

Theorem 2.2 Assume that Condition holds, and that are produced by New Scheme II. Then is monotonely decreasing and convergent to the solution of (1.2).

Proof Since all are M-matrices, in New Scheme II are well defined.

First, we prove is decreasing monotonically, i.e.,

(2.5)

By (2.3) we have

(2.6)

which combining with (2.1) and (2.2) yields

(2.7)

Since are M-matrices, (2.7) means

(2.8)

By (2.4) we obtain

(2.9)

By, (2.8) and (2.9) we know

(2.10)

and

(2.11)

which and (2.10) implies

Similarly, by (2.3) we derive

which combining with (2.2) and (2.6) implies

Hence we have

(2.12)

By (2.4), we have

(2.13)

By (2.12), (2.13) and, we know

(2.14)

which combining with and (2.11) we derive

(2.15)

By (2.11), (2.12) and (2.13) ,we get

which combining with (2.15) implies

It is easy to derive by induction that

(2.16)

and

(2.17)

It follows that (2.5) holds.

It follows from (2.2) and (2.3) that

(2.18)

Since the set is a finite set there exist positive integers and with such that

Therefore, we have

Then by (2.2) we obtain

which and (2.17) results in

(2.19)

From (2.4), (2.16) and (2.19) we have

(2.20)

It follows from (2.18), (2.19) and (2.20) that

which means is a solution of (1.2). The existence of solution has been proved.

Finally, we prove the uniqueness of solution. Assume and are solutions of (1.2), i.e.,

(2.21)

(2.22)

It is easy to see from (2.21) and (2.22) that there exist and such that

(2.23)

(2.24)

(2.25)

(2.26)

(2.23) and (2.26) implie. But (2.24) and (2.25) implies. Hence. The proof is complete. ,

3. Numerical Example

We use example 2 in [4] , i.e.,

(3.1)

where

The discretization of the above second order derivatives are:

where denote the forward and backward difference respectively in and, ,. We use New Scheme II to solve the discrete problem. Take, and 1.1, 1.3, 1.5, 1.8, 1.9 respectively.

Table 1 and Table 2 show the ∞-norm of the residual when iteration terminates.

We see that for and is big for.

Table 3 shows the relation between iteration number and relaxation number. Table 4 and Table 5 show the value of at for and respectively.

We can see from Table 3 that the algorithm for is faster than that for. Table 4 and Table 5 display the monotonicity of the algorithm.

Table 1. ∞-norm of the residual R.

Table 2. ∞-norm of the residual R.

Table 3. Iteration number m.

Table 4. The value of at.

Table 5. The value of at.

Funding

This work was supported by Educational Commission of Guangdong Province, China (No. 2012LYM-0066) and the National Social Science Foundation of China (No. 14CJL016).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Lions, P.L. and Mercier, B. (1980) Approximation numerique des equations de Hamilton-Jacobi-Bellman. RAIRO Numerical Analysis, 14, 369-393.
[2]	Bensoussan, A. and Lions, J.L. (1982) Applications of Variational Inequalities in Stochastic Control. North-Holland, Amsterdam.
[3]	Boulbrachene, M. and Haiour, M. (2001) The Finite Element Approximation of Hamilton-Jacobi-Bellman Equations. Computers & Mathematics with Applications, 14, 993-1007. http://dx.doi.org/10.1016/S0898-1221(00)00334-5
[4]	Hoppe, R.H.W. (1986) Multigrid Methods for Hamilton-Jacobi-Belman Equations. Numerische Mathematik, 49, 239-254. http://dx.doi.org/10.1007/BF01389627
[5]	Huang, C.S., Wang, S. and Teo, K.S. (2004) On Application of an Alternating Direction Method to HJB Equations. Journal of Computational and Applied Mathematics, 166, 153-166. http://dx.doi.org/10.1016/j.cam.2003.09.031
[6]	Sun, M. (1993) Domain Decomposition Method for Solving HJB Equations. Numerical Functional Analysis and Optimization, 14, 145-166. http://dx.doi.org/10.1080/01630569308816513
[7]	Sun, M. (1996) Alternating Direction Algorithms for Solving HJB Equations. Applied Mathematics and Optimization, 34, 267-277. http://dx.doi.org/10.1007/BF01182626
[8]	Young, D. (1971) Iterative Solution of Large Linear Systems. AP, New York.
[9]	Zhou, S.Z. and Chen, G.H. (2005) A Monotone Iterative Algorithm for a Discrete HJB Equation. Mathematica Applicata, 18, 639-643. (in Chinese)
[10]	Zhou, S.Z. and Zhan, W.P. (2003) A New Domain Decomposition Method for an HJB Equation. Journal of Computational and Applied Mathematics, 159, 195-204. http://dx.doi.org/10.1016/S0377-0427(03)00554-5
[11]	Zhou, S.Z. and Zou, Z.Y. (2008) An Itetative Algorithm for a Quasivariational Inequality System Related to HJB Equation. Journal of Computational and Applied Mathematics, 219, 1-8. http://dx.doi.org/10.1016/j.cam.2007.07.013
[12]	Zhou, S.Z. and Zou, Z.Y. (2008) A New Iterative Method for Discrete HJB Equations. Numerische Mathematik, 111, 159-167. http://dx.doi.org/10.1007/s00211-008-0166-6
[13]	Zhou, S.Z. and Zou, Z.Y. (2007) A Relaxation Scheme for Hamilton-Jacobi-Bellman Equations. Applied Mathematics and Computation, 186, 806-813. http://dx.doi.org/10.1016/j.amc.2006.08.025