Thermoelectric Figure of Merit of a Material Consisting of Particles in Dependency on the Parameters of a Material ()
1. Introduction
The efficiency of the direct conversion of heat energy into electric current energy using solids is characterized by the dimensionless thermoelectric figure of merit of a material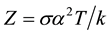 , where
, where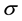 ,
, 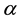 , T and k are the electrical conductivity, differential thermopower, absolute temperature and thermal conductivity of the material, respectively. Numerous and long-term studies have not resulted yet in developing materials with Z > 2 (see, for instance, [1] -[9] ).
, T and k are the electrical conductivity, differential thermopower, absolute temperature and thermal conductivity of the material, respectively. Numerous and long-term studies have not resulted yet in developing materials with Z > 2 (see, for instance, [1] -[9] ).
In this paper we discuss the problem of a material with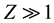 .
.
2. Model and Its Research
We shall consider the thermoelectric properties of a material consisting of a large number of identical ball- shaped non-degenerate n-type semiconductor particles contacting each other and metal particles with a n-type semiconductor thin film on the surface thereof. The phonon component of the material’s thermal conductivity is zero as the point contact area is zero. This type of material has electronic thermal conductivity made possible by electron tunneling through the vacuum gaps between the particles near the point contacts. We shall calculate the Z parameter of this material. We shall simplify the task and assume that the particles make a simple cubical lattice, also we shall assume the material temperature Т = 300 - 800 K and the particles diameter d = 10−6 - 10−3 m.
We shall offer the following symbols:
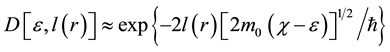
is the potential barrier transparency coefficient for the electrons tunneling from particle into particle through the gap between them; 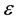 is the energy of electrons in a solid;
is the energy of electrons in a solid; 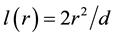 is the vacuum gap between the particles at the contact between them; r being the distance from the particles contact point in the plane x = 0, tangent to the particles spherical surfaces;
is the vacuum gap between the particles at the contact between them; r being the distance from the particles contact point in the plane x = 0, tangent to the particles spherical surfaces; 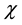 is the potential barrier which the electrons cross and which equals the electron affinity of the particles surface (in vacuum).
is the potential barrier which the electrons cross and which equals the electron affinity of the particles surface (in vacuum).
We shall compare the thermal conductivities k and 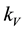 of the structure and of a homogeneous semiconductor respectively. We shall assume that the electron tunneling happens mostly through the gaps
of the structure and of a homogeneous semiconductor respectively. We shall assume that the electron tunneling happens mostly through the gaps  nm wide, that is through the area
nm wide, that is through the area , so
, so , where
, where  is the area diameter through which electrons mainly tunnel from one particle into another, and
is the area diameter through which electrons mainly tunnel from one particle into another, and 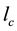 is the maximum gap between the particles that is tunnel-penetrable for electrons (Figure 1). If a constant temperature gradient
is the maximum gap between the particles that is tunnel-penetrable for electrons (Figure 1). If a constant temperature gradient 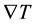 along the particle chain is established, there emerge a temperature difference
along the particle chain is established, there emerge a temperature difference  and a potential difference u between two particles. We can make an evaluation:
and a potential difference u between two particles. We can make an evaluation:![]() , where
, where ![]() and
and ![]() are the temperature diffusivity coefficients of the structure and of a homogeneous semiconductor respectively. As
are the temperature diffusivity coefficients of the structure and of a homogeneous semiconductor respectively. As![]() , temperature equalization rate within a particle is rather high, so when passing the border between particles in the contact area temperature changes stepwise by value
, temperature equalization rate within a particle is rather high, so when passing the border between particles in the contact area temperature changes stepwise by value![]() . Within each particle the solution of the stationary thermal conductivity equation
. Within each particle the solution of the stationary thermal conductivity equation ![]() shall be
shall be![]() .
.
The electron fluxes through the contact region between two particles in the forward and backward directions coincide:
![]() , (1)
, (1)
where
![]() , (2)
, (2)
e is the elementary charge; kB is the Boltzmann constant; ![]() or
or![]() ; n is the electron concentration within a
; n is the electron concentration within a
particle,![]() ; F is the Fermi level;
; F is the Fermi level; ![]() is the level of the conduc-
is the level of the conduc-
tion band bottom in the semiconductor; ![]() is the projection of the electron velocity vector onto the normal to the plane x = 0;
is the projection of the electron velocity vector onto the normal to the plane x = 0;![]() ; p and m are the electron momentum and effective electron mass;
; p and m are the electron momentum and effective electron mass;
![]() or
or![]() ;
; ![]() is the energy distribution function of electron. Using Expression (1), we shall find the differential thermopower of the material:
is the energy distribution function of electron. Using Expression (1), we shall find the differential thermopower of the material:
![]() (3)
(3)
![]()
Figure 1. Schematic diagram of the contact between two identical ball-shaped particles 1 and 2: l(r) is the gap between the particles at their contact, L―the thickness of the semiconductor film.
Let electric potential gradient ![]() be created in the material. We use the estimate
be created in the material. We use the estimate ![]() (see Figure 1), where
(see Figure 1), where ![]() and
and ![]() are the electrical conductivities of the structure and a homogeneous semiconductor, respectively. That means that the voltage drop within the particle is weak, the voltage drop in the contact area between two particles is
are the electrical conductivities of the structure and a homogeneous semiconductor, respectively. That means that the voltage drop within the particle is weak, the voltage drop in the contact area between two particles is![]() . The electric current through the contact is (see Equation (1)):
. The electric current through the contact is (see Equation (1)):
![]() .
.
If the condition ![]() is met, we use Equation (1) and the equality
is met, we use Equation (1) and the equality ![]() and write the electrical conductivity of the material as
and write the electrical conductivity of the material as
![]() . (4)
. (4)
The heat flow![]() , transferred by electrons through the contact zone of the two particles is calculated by the formula
, transferred by electrons through the contact zone of the two particles is calculated by the formula
![]() , (5)
, (5)
where
![]() , (6)
, (6)
![]() or
or![]() . Using the expression
. Using the expression![]() , we find the electronic thermal conductivity of the structure:
, we find the electronic thermal conductivity of the structure:
![]() . (7)
. (7)
The heat flow caused by the radiative heat exchange between two particles by means of thermal radiation and
the radiant thermal conductivity of the material are then![]() , and
, and
![]() , (8)
, (8)
respectively with![]() ―the Stefen-Boltzmann constant.
―the Stefen-Boltzmann constant.
Let us assume that the space between the particles is filled with a dielectric. In this case the potential barrier ![]() which the electrons cross equals the semiconductor and dielectric thermionic works difference. The heat flow qp, transferred by phonons through the contact area between two particles can be found using the formula:
which the electrons cross equals the semiconductor and dielectric thermionic works difference. The heat flow qp, transferred by phonons through the contact area between two particles can be found using the formula:
![]() ,
,
where ![]() is the dielectric thermal conductivity;
is the dielectric thermal conductivity;![]() ;
; ![]() is the gap between the particles were the dielectric molecules cannot enter. That means that the phonon thermal conductivity of the structure equals
is the gap between the particles were the dielectric molecules cannot enter. That means that the phonon thermal conductivity of the structure equals
![]() . (9)
. (9)
Consider the thermoelectric properties of the material, consisting of a large number of identical spherical metal particles with a n-type semiconductor thin film on the surface thereof. We assume that the following conditions are met:![]() ;
;![]() , where
, where![]() ―the thickness of the semiconductor film;
―the thickness of the semiconductor film;![]() ―the de Broglie wavelength of electrons in the metal particles. In this case we have
―the de Broglie wavelength of electrons in the metal particles. In this case we have
![]() ; (10)
; (10)
![]() (11)
(11)
![]() ; (12)
; (12)
![]() ; (13)
; (13)
![]() ; (14)
; (14)
![]() ;
;
![]() ;
;![]() ;
;
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
![]() ,
,
![]() (18)
(18)
where![]() ;
;![]() ―the potential barrier for electrons in the metal at the interface of the metal with
―the potential barrier for electrons in the metal at the interface of the metal with
the semiconductor film [10] ; ![]() and
and![]() ―the projection of the velocity vector of the electrons in the metal and the semiconductor, respectively, to the direction normal to the plane x = 0;
―the projection of the velocity vector of the electrons in the metal and the semiconductor, respectively, to the direction normal to the plane x = 0;![]() ―the width of the potential barrier;
―the width of the potential barrier;![]() ―thermionic work function of the surface of semiconductor films;
―thermionic work function of the surface of semiconductor films;
![]() ;
;![]() ―the voltage drop across semiconductor films;
―the voltage drop across semiconductor films;![]() ―voltage drop across the
―voltage drop across the
vacuum gap between the two particles;![]() .
.
We now use the spherical coordinate system for the volume element ![]() in the momentum space and the expression
in the momentum space and the expression![]() . Integrating with respect to θ in the limits from 0 to π/2 and with respect to
. Integrating with respect to θ in the limits from 0 to π/2 and with respect to ![]() from 0 to 2π and using Equation (10), (15) - (17), we find
from 0 to 2π and using Equation (10), (15) - (17), we find
![]() , (19)
, (19)
![]() , (20)
, (20)
where![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() .
.
Expressions (1), (3), (7), (8), (9) and (11) - (20) were used to perform computer calculations of the values![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() , with
, with ![]() or
or![]() . Parameters T;
. Parameters T;![]() ;
;![]() ;
; ![]() and d were varied, values
and d were varied, values![]() ;
;![]() ;
;![]() ;
; ![]() were constant.
were constant.
Example of the calculated curves![]() ,
, ![]() at different film thicknesses L nondegenerate semiconductor films on their surfaces are presented in Figure 2. By increasing L, the thermoelectric figure of merit of a material increases monotonically, approaching its limiting value.
at different film thicknesses L nondegenerate semiconductor films on their surfaces are presented in Figure 2. By increasing L, the thermoelectric figure of merit of a material increases monotonically, approaching its limiting value.
We shall consider the thermoelectric properties of a material consisting of a large number of identical ball- shaped non-degenerate n-type semiconductor particles contacting each other. In the range of values![]() ,
,
the values![]() ,
, ![]() and Z are not dependent on
and Z are not dependent on![]() , if T » 300 K;
, if T » 300 K;![]() ;
;![]() ;
; ![]() . Examples of the calculated curves
. Examples of the calculated curves ![]() and Z(T) are presented in Figure 3 and Figure 4. The maximum value
and Z(T) are presented in Figure 3 and Figure 4. The maximum value![]() . If the particle diameter is enlarged while the other parameters are held constant at the
. If the particle diameter is enlarged while the other parameters are held constant at the![]() , the value
, the value ![]() decreases monotonously (by a factor of ten or so) due to the increase of the radiant thermal exchange role in the material’s thermal conductivity (see, for instance, Figure 3, curve 3). If the electron potential barrier
decreases monotonously (by a factor of ten or so) due to the increase of the radiant thermal exchange role in the material’s thermal conductivity (see, for instance, Figure 3, curve 3). If the electron potential barrier ![]() is enlarged, the dependency
is enlarged, the dependency ![]() includes the maximum at the
includes the maximum at the ![]()
![]() , where
, where ![]() depends on the temperature. Then, in the presence of an insulator between the particles (kd ≥ 1 W/m∙K), Z(χ) continues to decrease rapidly and monotonically.
depends on the temperature. Then, in the presence of an insulator between the particles (kd ≥ 1 W/m∙K), Z(χ) continues to decrease rapidly and monotonically.
In the range ![]() these calculated
these calculated ![]() independent values are equal to the values calculated by the formulas:
independent values are equal to the values calculated by the formulas:
![]()
Figure 2. Thermoelectric figure of merit of a material consisting of metal particles vs. the potential barrier to electrons tunneling through the gap between the particles with different thicknesses of the semiconductor films on the surface of the metal particles. L = (1) 0, (2) 1 and (3) 3 nm. D = 10?6 m; Т = 700 K; Ec ? F = 0.2 eV; kd = 0.
![]()
Figure 3. Thermoelectric figure of merit of a material consisting of semiconductor particles vs. the particles diameter with other parameters held constant. (Ec − F) = (1), (2) and (3) 0.05 eV; χ = (1) 0.7, (2) 0.3 and (3) 1.5 eV; Т = (1), (2) 600 and (3) 300 K; kd = (1), (3) 0 and (2) 1 W/(m∙K).
![]()
Figure 4. Thermoelectric figure of merit of a material consisting of semiconductor particles vs. the temperature of a material. (Ec − F) = (1), (3) 0.15, and (2) 0.05 eV; χ = (1) 0.7, (2) 0.3 and (3) 2 eV; d = (1), (2) 10−3 and (3) 10−6 m; kd = (1), (3) 0 and (2) 1 W/(mK).
![]()
(see, for instance, Figure 3 and Figure 4, curves 3). We can demonstrate that those formulas can be found with the use of the Formulas (1) - (7) if the following conditions are met ![]() and in the Formulas (2), (6)
and in the Formulas (2), (6) ![]() .
.
3. Conclusion
Thus the currently existing semiconductor particles can be used to produce structures with the thermoelectric figure of merit Z = 10 - 100, if the thermionic work function of the particle surface ![]() is lower than 1 eV. If the semiconductor particles diameter (d
is lower than 1 eV. If the semiconductor particles diameter (d ![]() 10?5 m) is enlarged and
10?5 m) is enlarged and ![]() while the other parameters are held constant, the value
while the other parameters are held constant, the value ![]() increases monotonously. When the temperature of a material increases, the thermoelectric figure of merit increases, if
increases monotonously. When the temperature of a material increases, the thermoelectric figure of merit increases, if![]() . By increasing thicknesses of the semiconductor films on the surface of the metal particles, the thermoelectric figure of merit of a material increases monotonically, approaching its limiting value.
. By increasing thicknesses of the semiconductor films on the surface of the metal particles, the thermoelectric figure of merit of a material increases monotonically, approaching its limiting value.
Acknowledgements
This work was supported by the Russian Foundation for Basic Research (project no. 12-02-97500) and the authorities of
Orel
oblast.