1. Introduction
Fick’s classical diffusion equation is so much a part of the scientific folklore that I decided to revisit its original derivation and the underlying experiments in a graduate course. To my surprise, Fick’s own experiments turned out to be remarkably accurate and the geometry of his funnel experiments could be adequately reconstructed. While searching for Fick’s original publications, a student in the class found on the Web an antique book dealer who had the first edition of Fick’s handbook on medical physics, which I quickly purchased. I then asked my neighbor who is German by birth and education to help me in the translation of the relevant sections of the book and she kindly agreed. The book was written by Fick as an account of physics applicable to medicine and it brings interesting insights into Fick’s way of thinking about diffusion and osmosis, see Part II. The book section on the diffusion in liquids is more personal and somewhat different from the two famous papers published one year earlier (Fick, 1855a; Fick, 1855b) .
This paper is a simple evaluation of Fick’s original experiments based on the theory of diffusion presented so well in (Hirschfelder et al., 1954) and (Bird et al., 1960) . For an exquisite and brief discussion of the various theories of diffusion developed over the decades by Maxwell, Stefan, Onsager, Chapman and Enskog, Eckart and Meixner, and many others, one may refer to (Truesdell, 1962) .
Fick’s theory of diffusion is almost as old as the theories of heat conduction by Fourier (Fourier, 1807; Fourier, 1822) and viscosity by Newton. While originally it was too primitive to reveal any ideas of principle, Maxwell soon1 gave it a rational basis in his kinetic theory of gas mixtures and Stefan (Stefan, 1871) cleared away the specifically kinetic details to achieve an inclusive phenomenological theory, see (Truesdell, 1966) for further details.
2. Background
For convenience, a few pertinent equations describing diffusion will be listed here. A full derivation may be found in, e.g., (Bird et al., 1960) . Let  denote the velocity of constituent2 B of a fluid mixture with respect to a stationary coordinate system, and define this velocity as by taking a snapshot of instantaneous velocities of the molecules of B. For a mixture of
denote the velocity of constituent2 B of a fluid mixture with respect to a stationary coordinate system, and define this velocity as by taking a snapshot of instantaneous velocities of the molecules of B. For a mixture of  constituents, we define the local mass-average velocity as
constituents, we define the local mass-average velocity as
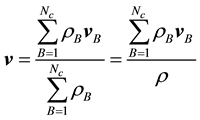 (1)
(1)
Thus  is the local rate at which mass passes through a unit area perpendicular to
is the local rate at which mass passes through a unit area perpendicular to . Similarly, we may define a local molar average velocity as
. Similarly, we may define a local molar average velocity as
 (2)
(2)
Thus  is the local rate at which moles pass through a unit area perpendicular to
is the local rate at which moles pass through a unit area perpendicular to .
.
In flow systems one is often interested in the velocity of a given constituent with respect to 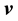 or
or , rather than with respect to a stationary coordinate system. This leads to the following definition of the diffusion velocities:
, rather than with respect to a stationary coordinate system. This leads to the following definition of the diffusion velocities:
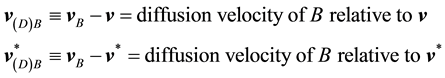 (3)
(3)
These velocities measure the motion of constituent B in a fluid relative to the local mean motion of the fluid.
Now we can define the different mass and molar fluxes. The mass or molar flux of constituent B is defined as a vector whose magnitude is equal to the mass or moles of constituent B that pass through a unit area per unit time. The motion may be referred to stationary coordinates, to the local mass-average velocity, 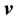 , or to the local molar-average velocity,
, or to the local molar-average velocity,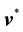 . Thus the mass and molar flux densities relative to stationary coordinates are
. Thus the mass and molar flux densities relative to stationary coordinates are
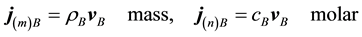 (4)
(4)
The mass and molar flux densities relative to the mass-average velocity 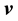 are
are
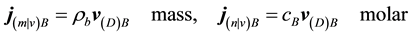 (5)
(5)
and the mass and molar flux densities relative to the molar-average velocity ![]() are
are
![]() (6)
(6)
Again, one should remember that the definition of a mass flux density is incomplete until both the units and the frame of reference are given.
By analogy with the flux of energy in one-dimensional systems:
![]() (Fourier’s law for constant
(Fourier’s law for constant![]() ), (7)
), (7)
one may define the mass flux of constituent 1 in a binary system 12 as
![]() (Fourier’s law for constant
(Fourier’s law for constant![]() ) (8)
) (8)
Note that the total mass density, ![]() , of the mixture is uniform, i.e., constant given a constant temperature. Here
, of the mixture is uniform, i.e., constant given a constant temperature. Here ![]() is the thermal diffusivity,
is the thermal diffusivity, ![]() is the heat capacity,
is the heat capacity, ![]() is the diffusion coefficient, and
is the diffusion coefficient, and ![]() is the mass density of constituent 1.
is the mass density of constituent 1.
If the fluid density is not uniform, one defines the mass diffusivity ![]() in a binary system in an analogous fashion:
in a binary system in an analogous fashion:
![]() (9)
(9)
Note that Equation (9) is purely kinematic, i.e., it involves only the dimensions of length and time, and it must be justified from an independent dynamic theory that invokes forces.
It may easily be shown (Bird et al., 1960) that the mass or molar diffusion fluxes in Equation (9) are also given by
![]() (10)
(10)
These two relationships are of special importance for this paper.
Fick’s experiment (Fick, 1855b) in a cylindrical tube is shown in Figure 1. At![]() , salt (1) diffuses into fresh water (2), while solid salt in a salt reservoir dissolves, replenishing the diffusing salt, and maintaining the
, salt (1) diffuses into fresh water (2), while solid salt in a salt reservoir dissolves, replenishing the diffusing salt, and maintaining the
![]()
Figure 1. Fick’s diffusion experiment in a cylindrical tube with a salt reservoir at the bottom and flowing fresh water at the top.
saturated salt concentration at![]() . A stream of fresh water sweeps the salt emerging from the tube, keeping the zero salt concentration at
. A stream of fresh water sweeps the salt emerging from the tube, keeping the zero salt concentration at![]() . The whole system is at constant (albeit unknown) temperature and pressure. The mixture of salt and water is assumed ideal, i.e., each component activity is equal to its mole fraction.
. The whole system is at constant (albeit unknown) temperature and pressure. The mixture of salt and water is assumed ideal, i.e., each component activity is equal to its mole fraction.
When this dissolving salt system attains a steady state, there is a net motion of salt away from the salt reservoir and the water in the tube is stationary. Hence we can use expression (10)2 for the molar flux of salt relative to a stationary frame of reference:
![]() (11)
(11)
The salt mass balance over an incremental column height, dz states that at steady state
![]() (12)
(12)
Substitution of Equation (11) into Equation (12) gives
![]() (13)
(13)
We shall assume that D12 is nearly independent of concentration. Indeed the literature data show that D12 ≈ 1 cm2/day for 0.1 - 1 normal salt solutions. The saturated salt concentration is about 36 g NaCl/100g of water or 26 g NaCl/100g solution at room temperatures of 10 - 20 degrees C. From Appendix, we can calculate the total concentration of water and salt at 20 deg C. This calculation is summarized in Table 1. The percent coefficient of variation is generally less than 1%; therefore, the total concentration can be assumed constant.
The coefficient of variation is defined as ![]()
Thus, we can recast the steady state diffusion mass balance of salt, Equation (13), as
![]()
Table 1. Total concentration of aqueous salt solutions, see Appendix.
![]() (14)
(14)
This equation can be easily solved (Bird et al., 1960) and the result is
![]() (15)
(15)
The density-mole concentration data from Table 1 and Table 2 are summarized in Table 3. The latter table can be used in conjunction with the excess gravities reported by Fick to convert his gravity versus depth results into the salt mole fraction versus depth. This was implemented as linear interpolation.
The results are shown in Figure 2. Agreement between the theory and experiment is excellent.
Remarks
Figure 3 shows the profile of excess gravity that would have been calculated by Fick for the cylindrical tube experiment. Note that there is a systematic deviation of the calculation from the experimental data. Fick himself said (Fick, 1855a) : “That the degrees of concentration in the lower layers decrease a little more slowly than in the upper ones, is easily explained by the consideration, that the stationary condition had not been perfectly attained”. Similar excuses have been used by experimentalists ever since.
3. Fick’s Conical Funnel Experiment
The conical funnel data obtained by Fick (Fick, 1855a) are more difficult to decipher because of the incomplete reporting of the experiment. The most likely experiment geometry may be inferred from Figure 6. In an inverted
![]()
Table 2. Density and concentrations of aqueous NaCl solutions at 20 deg C.
The concentration units are explained above. The correction δ is as follows: if the solution density is determined at the temperature T1 in deg C, then one adds ![]() to this density to obtain the corresponding solution density at the temperature T2. The numeric value of specific gravity of a solution relative to the specific gravity of water at 4 degrees C is identical to the numeric value of the solution density in g/cc. Data source is (Achmatowicz et al., 1954a, 1954b) .
to this density to obtain the corresponding solution density at the temperature T2. The numeric value of specific gravity of a solution relative to the specific gravity of water at 4 degrees C is identical to the numeric value of the solution density in g/cc. Data source is (Achmatowicz et al., 1954a, 1954b) .
![]()
Table 3. Salt solution density at 20 deg C and the mole fraction of salt.
![]()
Figure 2. Fick’s cylindrical tube excess gravities (+) have been converted to mole fractions of salt versus depth by linear interpolation of data in Table 3. The theoretical curve given by Equation (15) is the solid line. Note excellent agreement between theory and experiment.
![]()
Figure 3. This is how Fick would interpret his cylindrical tube experiment. Note the systematic deviation between the data and the straight line drawn by Fick.
conical funnel, and in the absence of gravity, the salt concentration contours would be sections of concentric spheres centered on the salt reservoir at the funnel tip. One may argue that in the gravitational field the spherical concentration profiles of salt will be flattened vigorously by buoyancy force3. The denser salt solution near the funnel axis will sink, while the less dense solution near the walls will be buoyed. The concentration profiles will then become almost perfectly horizontal. With help of Figure 4, this assertion can be proven as follows. For the salt profile flattening to happen, the ratio of the characteristic time of diffusion, ![]() spreading the salt radially, and convection,
spreading the salt radially, and convection, ![]() , tumbling the more concentrated salt solution down a “hill” of height h, must be much more than one:
, tumbling the more concentrated salt solution down a “hill” of height h, must be much more than one:
Fick’s Number Fi![]() , (16)
, (16)
i.e., buoyancy flattens the constant salt concentration profiles before diffusion propagates them as sections of concentric spheres.
The characteristic diffusion time scale can be obtained from the diffusion coefficient, D12, and the distance, h:
![]() (17)
(17)
Assuming no viscous dissipation, the shortest convection time scale can be obtained from the balance of potential and kinetic energy:
![]() (18)
(18)
![]()
Figure 4. Geometry of flattening of diffusion front.
From elementary geometry, it also follows that
![]() (19)
(19)
By combining Equations (16)-(19), one obtains the following criterion
![]() (20)
(20)
The plot of the critical distance from the salt reservoir with the most conservative ![]() is given in Figure 5. It is obvious that at distances of more than 1 mm above the salt reservoir, the salt concentration profiles are essentially flat.
is given in Figure 5. It is obvious that at distances of more than 1 mm above the salt reservoir, the salt concentration profiles are essentially flat.
The geometry of Fick’s cemented funnel experiments is shown in Figure 6. The junction between the funnel and the salt reservoir is at an unknown elevation ![]() at which the salt solution is saturated. Because the deepest reported salt density is far from the density of the saturated salt solution, there is an unknown offset
at which the salt solution is saturated. Because the deepest reported salt density is far from the density of the saturated salt solution, there is an unknown offset ![]() between
between ![]() and the deepest measurement.
and the deepest measurement.
In the cylindrical-polar coordinate system in Figure 6, the vertical diffusion flux is
![]() (21)
(21)
The salt mass balance over a cylinder with the base of ![]() and height
and height![]() , states that at steady state
, states that at steady state
![]() (22)
(22)
![]()
Figure 5. The critical distance from the salt reservoir at the tip of an inverted conical funnel versus the funnel half-angle. At distances much greater than the critical distance, the salt concentration profiles will be essentially flat.
![]()
Figure 6. Geometry of Fick’s funnel experiment.
Substitution of Equation (21) into Equation (22) and assumption of constant ![]() give
give
![]() (23)
(23)
Equation (23) can be readily solved (Bird et al., 1960) and the result is
![]() (24)
(24)
To match Fick’s results with the theoretical curve (24), one needs to find the lower elevation ![]() and the measurement offset
and the measurement offset![]() . Then
. Then![]() . The resulting two-parameter optimization problem has been solved using the Nelder-Mead amoeba algorithm and the solution is:
. The resulting two-parameter optimization problem has been solved using the Nelder-Mead amoeba algorithm and the solution is:
![]() (25)
(25)
Without invoking a nonzero offset, Fick’s experimental results cannot be matched. Thus, the funnel-salt reservoir junction corresponds to the elevation of 5 cm above the funnel tip and the deepest gravity measurement was preformed 3 cm above that junction. The resulting fit of Fick’s funnel data is shown in Figure 7. A little bit of scientific sleuthing has resulted in excellent agreement with Fick’s experimental data―a handsome reward indeed!
4. Discussion of Fick’s Equation
On no basis beyond an asserted analogy to Fourier’s analysis of the flow of heat, Fick proposed that in a binary mixture the diffusion mass flux density vector is proportional to the gradient of mass density:
![]() (26)
(26)
where D is a phenomenological coefficient which may depend upon the densities and the temperature.
From Equation (9) we now know that Equation (26) holds only if the solution density is constant:
![]()
Figure 7. Fick’s conical funnel excess gravities (+) have been converted to mole fractions of salt versus by linear interpolation of data in Table 3. The theoretical curve given by Equation (24) is the solid line. Note excellent agreement between the theory and Fick’s experiment.
![]() (27)
(27)
Because densities of Fick’s salt solutions varied by 20%, Fick in fact was mistaken in asserting Equation (26). His subsequent diffusion equation was derived from a shell mass balance between two horizontal planes dz apart.
Based on the mass balance shown in Figure 6, Fick derived the following equation:
![]() (28)
(28)
Instead of inserting the salt mass flux density from Equation (10) (he did not know this equation), Fick asserted Equation (26), and obtained the following equation:
![]() . (29)
. (29)
At steady state, and in the conical funnel whose radius is given as![]() , Fick simplified Equation (29) and solved it:
, Fick simplified Equation (29) and solved it:
![]() (30)
(30)
The two constants ![]() and
and ![]() “… are to be so determined, that for a certain z (where the cone is cut off and rests upon the salt reservoir4)
“… are to be so determined, that for a certain z (where the cone is cut off and rests upon the salt reservoir4) ![]() is equal to perfect saturation; and for a certain value of z which corresponds to the base of the funnel5,
is equal to perfect saturation; and for a certain value of z which corresponds to the base of the funnel5, ![]() becomes = 0”. Thus
becomes = 0”. Thus
![]() (31)
(31)
If Fick knew about Equation (10), then instead of Equation (30) he would have probably written:
![]() (32)
(32)
and he would have obtained Equation (23).
Because Fick does not report these “certain values of z”, to obtain the two constants we must use the elevation of the funnel base, and the offset of the deepest measurement calculated above. The two constants in Equation (30) are then readily calculated as![]() . In the paper, however, Fick lists his calculated salt density profile! The raw data, Fick’s calculation and the present calculation are shown in Figure 8. Agreement between the reconstructed solution and Fick’s “exact” calculation is very good indeed. The latter comparison confirms validity of the elevations (or axial distances) listed in Equation (25). Of course, because of the incorrect form of the governing equation, the solutions shown in Figure 8 are nowhere nearly as good as the solution shown in Figure 7.
. In the paper, however, Fick lists his calculated salt density profile! The raw data, Fick’s calculation and the present calculation are shown in Figure 8. Agreement between the reconstructed solution and Fick’s “exact” calculation is very good indeed. The latter comparison confirms validity of the elevations (or axial distances) listed in Equation (25). Of course, because of the incorrect form of the governing equation, the solutions shown in Figure 8 are nowhere nearly as good as the solution shown in Figure 7.
5. Conclusion
In general, Fick’s Equation (29) is not entirely correct. For the concentrated salt solutions, one may not assert that mass density ![]() is the appropriate unit of concentration, and that
is the appropriate unit of concentration, and that![]() . As it stands, after the sign correction, Fick’s original equation can only be applied to dilute solutions and to such tubes of variable cross- section whose walls are orthogonal to the surfaces of constant concentration. This does not detract however from
. As it stands, after the sign correction, Fick’s original equation can only be applied to dilute solutions and to such tubes of variable cross- section whose walls are orthogonal to the surfaces of constant concentration. This does not detract however from
![]()
Figure 8. Fick’s excess gravity data (+) in the conical funnel, his calculated salt density profile (upper curve), and the profile reconstructed here with use of the previously obtained values of z1 and δz.
Fick’s great physical insight, and from his creative and quite accurate6 experimental technique!
Acknowledgements
I thank Ms. Karin Lloyd-Mumford for her patience and tenacity in translating Fick’s difficult prose. I am grateful to the late Prof. T. N. Narasimhan for sharing his insights into the theories of diffusion and copies of the out-of-print books and papers.
Appendix―Different Units for Salt Concentrations
There are several ways of expressing salt concentrations (Achmatowicz et al., 1954a, 1954b) :
1) Number of grams of salt per 100 g of solution, c1;
2) Number of grams of salt per 100 g of water, c2;
3) Number of grams of salt per 1 liter of solution, mass concentration, c3;
4) Number of moles of salt per 1000 moles of water, c4;
5) Number of moles of salt per 1 liter of solution, molar concentration, c5;
6) Number of moles of salt per 1 kg of water, molality, c6;
7) Mole fraction of salt in water, c7;
Let ![]() denote the specific gravity of solution, and M the molecular weight of salt:
denote the specific gravity of solution, and M the molecular weight of salt:
![]() (A1)
(A1)
NOTES
1Maxwell published four important papers on gas theory, the first of which, “Illustrations of the Dynamical Theory of Gases”, appeared in 1860, and contained Maxwell’s first theory of diffusion. See (Garber et al., 1986) for details.
2“Constituent” denotes a chemical species or a pseudo-component.
![]()
3Fick was aware of this phenomenon; see the underlined sentences in Part II, Section 24.
![]()
4Fick used y instead of ρ1 and x instead of z. So his “certain distance x” becomes z = z1 in our notation.
5Equal to the outer elevation z2 in our notation.
![]()
6Fick remained modest about his approach: “… This method (of weighing an immersed glass bulb to determine density) creates little confidence at first sight, nevertheless preliminary experiments showed it to be sufficiently accurate”.