A Comparison of Higher-Order Active Band-Pass R-Filter Response with Equivalent Band-Pass RC-Filter Response at Varying Q-Factors ()
1. Introduction
In modern electronic circuits, unwanted signals are a major challenge to contend with. This is due to interferences in the form of noise and harmonics. These unwanted signals pose problem to certain specified desired bands of frequencies. In many state-of-the-art equipment or systems, such as receivers, EEG and FDM etc., high quality factors and fast roll-off rate filter networks are used to select/reject or separate/combine signals at different frequencies [1] . The common filters are the resistance-inductance-capacitance (RLC) based-filter networks. Others are the switched capacitor based filters using MOS switches rather than resistors or inductors. At high frequencies (≥1 MHz), inductance based filters are favourable, but become bulky and expensive at low-medium frequencies (≤1 MHz). The RC-filters utilizing operational amplifiers as active element and resistors and capacitors as passive elements are best suited for low-medium frequency responses. However, high quality capacitors having superior stability characteristics are also expensive and large in size, while physically small capacitors such as ceramic capacitors, exhibit relatively poor stability characteristics [2] [3] . These smaller capacitors when used as part of the filter capacitance may cause the filter to be highly Q-sensitive to circuit element value changes and thus exhibit unstable or severe amplitude peaking or attenuation [2] .
The development of capacitor-less filter (R-filter) network has eliminated these bulky components (thereby reducing cost of production) and has also enhanced the stability of the filters. The building block of the R-filter is the internally compensated operational amplifiers (Op-Amps) [4] [5] . In addition to frequency stabilization by the R-filter network, it also has the potential advantages of miniaturization, ease of design and high frequency performance [6] - [8] . Active R-filters have been reported to be suitable for medium-Q high frequency applica- tions [9] . The major disadvantages of the active R-filters were the temperature dependence of the filter centre frequency and the limited dynamic range due to Op-Amp slew rate limitations [10] . These disadvantages have been overcome by applying the active-R technique to current-feedback Op-Amps [10] .
Although, several papers have reported on the evaluation of the second-and third-order active R-filters [11] - [13] , we have not come across any reported circuit regarding direct cascading of circuits for the realization of higher-order active R-filter network and its comparison with an equivalent RC-filter network. This paper there- fore, is an attempt to design and simulate the sixth-order R- and RC-filter networks and to compare their fre- quency response characteristics based on their quality factors variation. It is not in doubt that higher-order filters provide higher gains as well as better frequency selectivity [14] .
2. Methodology
2.1. The R- and RC-Networks
The architecture that was used to implement both the sixth order active R-band pass filter and the sixth order active RC-filter is the multiple feed-back topologies. This topology was realized by cascading second order band pass filters of Figure 1 (stage 1 with single Op-Amp A1) and Figure 2 (stage 1 with operational amplifiers A11 and A12)
![]()
Figure 1. Sixth-order RC-filter network.
![]()
Figure 2. Sixth-order R-filter networks.
for RC- and R-band pass filters respectively. All operational amplifiers (Op-Amps) are of the 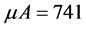 type of unity-gain frequency. The implementation of the designed filters utilized the
type of unity-gain frequency. The implementation of the designed filters utilized the 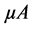 741 operational amplifiers,
741 operational amplifiers,  watt resistors with 5% tolerance and ceramic capacitors.
watt resistors with 5% tolerance and ceramic capacitors.
2.2. Theoretical Consideration of Band-Pass RC-Filter Network
Figure 1 presents a second-order band pass filter in a multiple-feedback configuration cascaded in three stages to form a sixth-order band-pass RC-filter network. The voltage divider at the input of stage 1 for example, consists of resistors 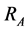 and
and 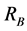 which serves as input attenuator to reduce gain. The voltage transfer function of a single stage of the filter network shown in Figure 1 can be expressed as [15] :
which serves as input attenuator to reduce gain. The voltage transfer function of a single stage of the filter network shown in Figure 1 can be expressed as [15] :
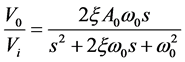 (1a)
(1a)
or in terms of quality factor, 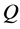 [9] :
[9] :
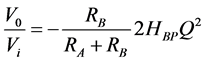 (1b)
(1b)
where 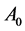 and
and 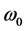 are the band-pass gain and open-loop 3 dB frequency (
are the band-pass gain and open-loop 3 dB frequency ( is gain band-width pro- duct) of the operational amplifier
is gain band-width pro- duct) of the operational amplifier 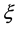 is the damping factor and
is the damping factor and
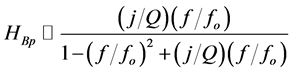 (1c)
(1c)
The quality factor, 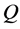 and the frequency
and the frequency ![]() in Equation (1) are given by Equations (3) and (4) as follows:
in Equation (1) are given by Equations (3) and (4) as follows:
![]() (2)
(2)
![]() (3)
(3)
From Equations (2) and (3), ![]() is the capacitance of the capacitor, which is assumed to have equal values, that is,
is the capacitance of the capacitor, which is assumed to have equal values, that is, ![]() and
and![]() . The resistors
. The resistors![]() ,
, ![]() , and
, and ![]() are related to the quality factor
are related to the quality factor ![]() by the Equation (4),
by the Equation (4),
![]() (4)
(4)
Design of Second-Order Band-Pass RC-Filter Network
The design parameters are that the filter should have a constant resonant frequency of 10 KHz at quality factors of 2, 5, 7, 8 and 10, respectively. First, we consider the design with a center frequency of 10 KHz and![]() . Also, for the purpose of simplification, we assume the capacitors have equal values of
. Also, for the purpose of simplification, we assume the capacitors have equal values of![]() . Therefore, from Equation (3), the value of resistor,
. Therefore, from Equation (3), the value of resistor, ![]() is calculated to be
is calculated to be
![]()
Using Equation (4) and choosing![]() ,
, ![]() was calculated to be 1999 Ω (2.0 kΩ). The open loop band pass gain was calculated using Equation (1) to be −40 dB (or 0.01).
was calculated to be 1999 Ω (2.0 kΩ). The open loop band pass gain was calculated using Equation (1) to be −40 dB (or 0.01).
Similar procedure was used to determine the resistor values![]() ,
, ![]() , and
, and ![]() for high quality factor
for high quality factor![]() , 7, 8, and 10. All calculated resistor values and their respective experimental values chosen for the implementa- tion of the second order RC-filter are presented in Table 1. To obtain a sixth-order RC-band pass filter, the sin- gle second-order filters designed above were cascaded as shown in Figure 1 and implemented using Multisim Electronic Workbench software.
, 7, 8, and 10. All calculated resistor values and their respective experimental values chosen for the implementa- tion of the second order RC-filter are presented in Table 1. To obtain a sixth-order RC-band pass filter, the sin- gle second-order filters designed above were cascaded as shown in Figure 1 and implemented using Multisim Electronic Workbench software.
2.3. Theoretical Consideration of Band-Pass R-Filter Network
Stage 1 of Figure 2 shows the second-order band pass R-filter used in this work to design the sixth-order band- pass R-filter configuration. The circuit was proposed by Shinde and Patil [5] . The second-order band-pass R- filter network in Figure 2 has a voltage transfer function:
![]() (5a)
(5a)
or in terms of quality factor,![]() .
.
![]()
Table 1. Resistor values for sixth-order RC-filter network at various Q-values.
![]() (5b)
(5b)
where ![]() is the gain-band width product of the operational amplifier,
is the gain-band width product of the operational amplifier, ![]() and
and ![]() are the attenuators formed by the voltage divider networks of resistors
are the attenuators formed by the voltage divider networks of resistors ![]() and
and ![]() (
(![]() and
and![]() ) and given in Equations (6a) and (6b):
) and given in Equations (6a) and (6b):
![]() (6a)
(6a)
![]() (6b)
(6b)
The second-order band pass R-filter network in Figure 2 has resonance frequency, ![]() and mid-band gain,
and mid-band gain, ![]() given by Equations (7) and (8), respectively
given by Equations (7) and (8), respectively
![]() (7)
(7)
![]() (8a)
(8a)
But from Equation (6a),
![]() (8b)
(8b)
Therefore, from Equations (8a) and (8b) the gain, ![]() can be simplified as follows:
can be simplified as follows:
![]() (9a)
(9a)
For cascaded band-pass R-filter with multiple feedbacks, the gain can be expressed as:
![]() (9b)
(9b)
From Equations (7) and (8), it can be seen that the resonance frequency is dependent on the voltage divider network formed by ![]() and
and ![]() at the non-inverting inputs of the two Ops, while the mid-band gain can be tuned by the voltage divider formed by
at the non-inverting inputs of the two Ops, while the mid-band gain can be tuned by the voltage divider formed by ![]() and
and ![]() at the inverting input of the second Op.
at the inverting input of the second Op.
Design of Second-Order Band-Pass R-Filter Network
First, we consider the design of second-order band pass R-filter (stage 1) with resonant frequency of 10 KHz, ![]() and
and ![]() [16] . Choosing
[16] . Choosing ![]() from Equation (7) we have
from Equation (7) we have ![]() (choose 100 KΩ). From Equation (8b) and taking the value of
(choose 100 KΩ). From Equation (8b) and taking the value of ![]() as 10 KΩ
as 10 KΩ![]() yield
yield![]() . The value of filter gain calculated from Equation (9) is 1.73 (4.76 dB). All calculated component values are presented in Table 2. The experimental values (with 1% tolerance) used to realize the band pass filters are also presented in Table 3.
. The value of filter gain calculated from Equation (9) is 1.73 (4.76 dB). All calculated component values are presented in Table 2. The experimental values (with 1% tolerance) used to realize the band pass filters are also presented in Table 3.
Similar calculations for the component values were carried out using Equation (7) to (11) for higher ![]() -va- lues (
-va- lues (![]() , 7, 8, and 10) with constant center frequency
, 7, 8, and 10) with constant center frequency![]() . To realize a sixth order configuration, the second order filters was cascaded as shown in Figure 2 and implemented using Multisim Electronic Work bench software.
. To realize a sixth order configuration, the second order filters was cascaded as shown in Figure 2 and implemented using Multisim Electronic Work bench software.
3. Results and Discussion
Figure 3 shows the magnitude verses frequency response plot obtained from the output of the three cascading sections (stages 1, 2 and 3) of the sixth-order band pass R-filter with![]() . The plot shows a gradual increase in the mid-band gain and roll-off of the R-filter network obtained from the output of the first cascading section
. The plot shows a gradual increase in the mid-band gain and roll-off of the R-filter network obtained from the output of the first cascading section
![]()
Table 2. Resistor values for sixth-order R-filter network at various Q-values.
![]()
Table 3. R-filter sections response characteristics.
![]()
Figure 3. Cascaded R-filter sections (stages) magnitude response for Q = 8.
(stage 1) to the third section (stage 3). The band-width was however found to decrease monotonically with each additional section. From the result of the roll-off presented in Table 3, it seems each cascading section is pro- viding a single pole roll-off of ![]() According to Jecob [17] , the total roll-off
According to Jecob [17] , the total roll-off ![]() of n iden- tical first order sections in cascade is given by:
of n iden- tical first order sections in cascade is given by:
![]() (11)
(11)
Thus, for the three cascading stages (Figure 2), ![]() and the result in Table 3 shows consistency with the above argument. This observation is contrary to report by Shinde et al. [8] that each section is a two pole net- work. The total roll-off
and the result in Table 3 shows consistency with the above argument. This observation is contrary to report by Shinde et al. [8] that each section is a two pole net- work. The total roll-off ![]() of the R-filter network in Figure 2 is close to the ideal value of
of the R-filter network in Figure 2 is close to the ideal value of ![]() for a third-order configuration (Figure 3 and Figure 4, Table 3). This is however not the case with the magni- tude-frequency response of the sixth-order RC-filter configuration presented in Figure 5. The
for a third-order configuration (Figure 3 and Figure 4, Table 3). This is however not the case with the magni- tude-frequency response of the sixth-order RC-filter configuration presented in Figure 5. The ![]() values (Table 4) approach that of the ideal sixth-order network given by
values (Table 4) approach that of the ideal sixth-order network given by ![]() [18] . A modification of Figure 4 to provide higher roll-off without the addition of a single component is possible as observed from a preliminary work carried out by these authors. The higher roll-off for the RC-filter network occurred in fre- quency band of no interest and parasitic effects are therefore “suspects” [19] .
[18] . A modification of Figure 4 to provide higher roll-off without the addition of a single component is possible as observed from a preliminary work carried out by these authors. The higher roll-off for the RC-filter network occurred in fre- quency band of no interest and parasitic effects are therefore “suspects” [19] .
The magnitude response of the cascaded R- and RC-band pass filters (for![]() , 5, 7, 8 and 10) are presented in Figure 4 and Figure 5, respectively. Both filter configurations show monotonic variations in the band-pass gain and band-width with increasing Q-values (see also Table 4). The highest mid-band gain and smallest band-width response was recorded for both R- and RC-filters for
, 5, 7, 8 and 10) are presented in Figure 4 and Figure 5, respectively. Both filter configurations show monotonic variations in the band-pass gain and band-width with increasing Q-values (see also Table 4). The highest mid-band gain and smallest band-width response was recorded for both R- and RC-filters for![]() , indicating better selectivity at higher quality factors. This observation is consistent with previous reports [14] . However, it is worth nothing that the R-filter network provided a positive gain and smaller band-width (Figure 4) when compared to the RC-filter network (Figure 5) at corresponding Q-values. This clearly suggests that the R-filter network provided better selectivity than the RC-filter network. Also, we observed a relative shift in the center-frequency towards lower frequencies with increasing Q-values for the RC-filter network (Figure 5), but the centre frequency
, indicating better selectivity at higher quality factors. This observation is consistent with previous reports [14] . However, it is worth nothing that the R-filter network provided a positive gain and smaller band-width (Figure 4) when compared to the RC-filter network (Figure 5) at corresponding Q-values. This clearly suggests that the R-filter network provided better selectivity than the RC-filter network. Also, we observed a relative shift in the center-frequency towards lower frequencies with increasing Q-values for the RC-filter network (Figure 5), but the centre frequency
![]()
Figure 4. Cascaded band pass magnitude response of R-filter for different Q-values.
![]()
Figure 5. Cascaded band pass magnitude response of RC-filter for different Q-values.
![]()
Table 4. Variation of functional properties (band-width, mid-band gain and roll-off) of R- and RC-filters.
remained fixed for the R-filter network (Figure 4). It is reported that higher Q values (e.g.![]() ) create cir- cuit instability and makes the circuit very sensitive to circuit component tolerances [2] . According to Attri [2] , capacitors are the real accuracy controlling and variation controlling components and so, precise capacitors are required in a multiple feedback topology (MFB) like the one presented in this work. Apart from the capacitors, the MFB topology is particularly very sensitive to the tolerance of the attenuator resistance RB and so requires precise resistors. Thus, the shift in the center frequency (particularly at
) create cir- cuit instability and makes the circuit very sensitive to circuit component tolerances [2] . According to Attri [2] , capacitors are the real accuracy controlling and variation controlling components and so, precise capacitors are required in a multiple feedback topology (MFB) like the one presented in this work. Apart from the capacitors, the MFB topology is particularly very sensitive to the tolerance of the attenuator resistance RB and so requires precise resistors. Thus, the shift in the center frequency (particularly at![]() ) can be attributed to the high to- lerance values of the resistors and the approximated values of resistors used in this design. The restriction to the commonly available resistor informed these approximations. These challenges are however absent in the ac- tive-R filter topology considered in this work thereby making it a better choice when compared to the RC-filter in the MFB topology.
) can be attributed to the high to- lerance values of the resistors and the approximated values of resistors used in this design. The restriction to the commonly available resistor informed these approximations. These challenges are however absent in the ac- tive-R filter topology considered in this work thereby making it a better choice when compared to the RC-filter in the MFB topology.
4. Conclusion
We have successfully designed and compared the band-pass responses of higher-order R- and RC-filter net works and found that in addition to the advantages of miniaturization, ease of design and high frequency per- formance, the R-filter network provides better selectivity, greater stop band attenuation and steeper cut-off at the edge of the pass band especially at higher Q-values. Also, no relative shift of the centre frequency was observed with R-filter network unlike the RC-filter network which had a relative shift of its centre frequency with Q. The low roll-off rate recorded for the three cascading sections of the R-filter indicate a third order configuration ra- ther than the proposed sixth order. Nevertheless, the three cascaded network can be modified to provide higher roll-off when desired.