The Exact Formulation of the Inverse of the Tridiagonal Matrix for Solving the 1D Poisson Equation with the Finite Difference Method ()
1. Introduction
The finite difference method is a very useful tool for discretizing and solving numerically a differential equation. It is effectively a classical method of approximation based on Taylor series expansions that has help during the last years theoretical results to gain in accuracy, stability and convergence.
In fact, this method is very useful for solving for example Poisson equation. This elliptic equation appears very often in mathematics, physics, chemistry, biology and engineering. In one dimension, the resolution leads to a tridiagonal matrix in the case of centered difference approximation. This matrix, which is diagonally dominant, can be inverted with methods such as Gauss elimination, Thomas Algorithm Method [1] . These technics are powerful and very efficient.
We proposed here, a new and direct method of inversion of this tridiagonal matrix independently of the right- hand side. For Dirichlet-Dirichlet boundary problems, this innovative method is faster than the Thomas Algorithm. It gives better accuracy and is far more economical in terms of memory occupation.
First, the finite difference method is presented for the 1D Poisson equation. Secondly, the properties of the matrix associated with the Laplacian and its inverse are discussed. Then, the inverse matrix is determined and its properties are analyzed. Thus, verification is done considering an interesting potential problem, and the sensibility of the method is quantified.
2. Finite Difference Method and 1D Poisson Equation
We consider a function 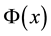 which satisfies the Poisson equation
which satisfies the Poisson equation , in the interval
, in the interval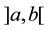 , where
, where  is a specified function.
is a specified function.  fulfills the Dirichlet-Dirichlet boundary conditions
fulfills the Dirichlet-Dirichlet boundary conditions 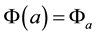 and
and . We consider an one-dimensional mesh with
. We consider an one-dimensional mesh with  discrete points
discrete points . Each point
. Each point 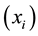 is de-
is de-
fined by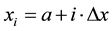 , where
, where  being the step size. We define
being the step size. We define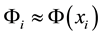 ,
, 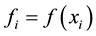 ,
, .
.
We have chosen the centered difference approximation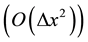 , in this work, for the fact that it gives a tridiagonal, diagonally dominant, and symmetric matrix. Considering all the above mentioned criteria, one can rewrite the 1D Poisson equation in a set of algebraic equations:
, in this work, for the fact that it gives a tridiagonal, diagonally dominant, and symmetric matrix. Considering all the above mentioned criteria, one can rewrite the 1D Poisson equation in a set of algebraic equations:
![]() (1)
(1)
One gets a linear system of ![]() equations, which can be written in a matrix form [2]
equations, which can be written in a matrix form [2]
![]() (2)
(2)
Thus, solving the 1D Poisson equation means to invert the negative definite, and regular ![]() -matrix
-matrix![]() . Its inverse, that we noted
. Its inverse, that we noted![]() , is also symmetric. Both matrices have the following properties:
, is also symmetric. Both matrices have the following properties:
![]() (3)
(3)
and
![]() (4)
(4)
where ![]() is the Kronecker’s delta.
is the Kronecker’s delta.
3. The Inverse of Matrix ![]()
From (4), we derive successively the following interesting relations:
![]() (5)
(5)
with (5), one sees that the matrix ![]() is entirely determined if the term
is entirely determined if the term ![]() is known. This term can be determined by observing the behavior of
is known. This term can be determined by observing the behavior of ![]() for different
for different ![]() values: It holds
values: It holds
![]() (6)
(6)
From (5) and (6), we get
![]() (7)
(7)
Now, the matrix ![]() is completely and exactly determined.
is completely and exactly determined. ![]() with
with
![]() (8)
(8)
![]()
The solution of the 1D Poisson equation is obtained with a simple, extremely fast matrix multiplication:![]() . Thus, the numerical resolution of the 1D Poisson equation which is an interesting topic in physics and engineering is made easy and very accurate.
. Thus, the numerical resolution of the 1D Poisson equation which is an interesting topic in physics and engineering is made easy and very accurate.
Analysis
A first analysis of the matrix ![]() let us believe that, this new method possesses an algorithm complexity of
let us believe that, this new method possesses an algorithm complexity of![]() , which is situated between the Gauss eliminations
, which is situated between the Gauss eliminations ![]() and the one of Thomas’s
and the one of Thomas’s ![]() [1] .
[1] .
A deeper analysis of the matrix ![]() shows that the complexity brought by the Thomas method is largely improved in this study. In addition, one can see a close link between its row vectors and column vectors.
shows that the complexity brought by the Thomas method is largely improved in this study. In addition, one can see a close link between its row vectors and column vectors.
The matrix ![]() is also persymmetric:
is also persymmetric:
![]()
All the information about it, can be found in the upper triangle (in gray color, see Figure 1).
Further, we can even find very interesting relations in this matrix which can help refining the final solution.
That is what we effectively did, and one can see a direct solution for ![]() at the point
at the point![]() , which can be expressed by
, which can be expressed by
![]() (9)
(9)
Also a direct solution for ![]() at the point
at the point ![]() is:
is:
![]() (10)
(10)
Generally, a very important recurrence relation can be obtained, which gives all solutions:
![]() (11)
(11)
which is equivalent to:
![]() (12)
(12)
This very innovative Equation (12) gives directly and accurately all the solution that we are looking for. It proves that our method is direct, faster than the one of Thomas’s in this context and gives as well better accuracy. Furthermore, it is far more economical in terms of memory occupation. This is due to the fact that the matrix ![]() does not necessitate to be generated. A programmer does not need to declare nor to define the matrix
does not necessitate to be generated. A programmer does not need to declare nor to define the matrix ![]() in his code.
in his code.
In conclusion to this, we can say that the matrix ![]() is the key of this efficient new method. This matrix
is the key of this efficient new method. This matrix![]() , which is the inverse of matrix
, which is the inverse of matrix![]() , is determined explicitly, directly, and independently of the right-hand side of the Poisson equation.
, is determined explicitly, directly, and independently of the right-hand side of the Poisson equation.
N.B.: One can prove using mathematical induction that![]() . It holds for the
. It holds for the ![]() cofactor of
cofactor of![]() :
:![]() . We call the matrix
. We call the matrix ![]() Bira’s Matrix.
Bira’s Matrix.
4. Verification with a Potential Problem
We consider a scalar potential![]() , defined in [0, 1], which satisfies
, defined in [0, 1], which satisfies
![]() .
. ![]() fulfills the following boundary conditions:
fulfills the following boundary conditions: ![]()
![]() . The exact solution is
. The exact solution is
![]() (13)
(13)
With the finite difference method, we take![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and![]() . The solution is
. The solution is
![]() (14)
(14)
Discussions
We define the variable![]() , which is the relative error at point
, which is the relative error at point ![]() for
for![]() .
. ![]() represents
represents![]() .
.
Generally, we have
![]() (15)
(15)
We can also define the average value of the relative error for a given![]() :
:![]() . For
. For![]() , it is:
, it is:![]() .
.
We obtain the following results, presented in Table 1.
The table shows that the solution is very accurate. Notwithstanding that we have been interested in determining the sensibility of the proposed method. Effectively, we have plotted ![]() for different
for different ![]() values.
values.
We obtain a hyperbola, which can be predicted as proportional to![]() .
.
This curve is fitted with a function which can be defined as
![]() (16)
(16)
where![]() . We obtain two curves represented in Figure 2.
. We obtain two curves represented in Figure 2.
![]()
Table 1. Results and relative error.
We realize that the average relative error ![]() behaves like a truncation error that we express in the fol-
behaves like a truncation error that we express in the fol-
lowing manner![]() .
. ![]() is the fourth order derivative of the
is the fourth order derivative of the ![]() function in a point (here
function in a point (here![]() ) which belongs to the interval
) which belongs to the interval![]() .
.
For our given function ![]() and also the results from the fitting, we have the following relations [3] :
and also the results from the fitting, we have the following relations [3] :
![]() (17)
(17)
This proves that the method is very accurate, naturally stable, robust, quick and precise.
5. Conclusions
This paper has provided a new improved method for solving the 1D Poisson equation with the finite difference
method. Accurate results have been obtained with a sensibility found to be as the function of![]() . In fact, the inverse of the tridiagonal matrix, which is associated with this differential equation, is determined directly, exactly, and independently to the right-hand side. Thus, a new formulation of the solution is given with an algorithmic complexity of O(N). With this innovative method, the 1D Poisson equation, with Dirichlet-Dirichlet boundary condition is solved, with only one programming loop. This new approach provides also gain in accuracy and economy in memory allocation.
. In fact, the inverse of the tridiagonal matrix, which is associated with this differential equation, is determined directly, exactly, and independently to the right-hand side. Thus, a new formulation of the solution is given with an algorithmic complexity of O(N). With this innovative method, the 1D Poisson equation, with Dirichlet-Dirichlet boundary condition is solved, with only one programming loop. This new approach provides also gain in accuracy and economy in memory allocation.
A future work can consider Neumann or mixed boundary conditions.
Acknowledgements
I would like to thank my colleagues Dr. Cheikh Mbow and Dr. Kharouna Talla for benefit discussions and remarks that contribute to improving the quality of this paper.