Encapsulating the Role of Solution Response Space Roughness on Global Optimal Solution: Application in Identification of Unknown Groundwater Pollution Sources ()
1. Introduction
Unknown groundwater pollution sources are characterised in terms of their location and source flux release history over time. In scenarios where the potential source locations are known with some degree of certainty, linked simulation-optimization approach is used for recreating the flux release history. In this approach, simulated aquifer response is compared to actual observed aquifer response due to a given pollutant source flux release pattern. The responses are compared in terms of the pollutant concentration measurements, taken from specified sparse monitoring locations at discrete time intervals over a monitoring time horizon. The objective functions for this comparison essentially minimizes the difference between the simulated and the observed response of the aquifer using the optimization model. Different mathematical formulations can be used to achieve this objective. However, different mathematical formulations show different levels of accuracy in source identification results. In this study, two different mathematical formulations of the same objective and their effect on the performance of the source identification models are presented.
The identification of unknown pollution sources is non-linear [1] , ill-posed inverse problem [2] . Optimization based approach for solving groundwater pollution source identification problem has been proposed by several researchers. Some of the initial contributions in identification of unknown groundwater pollution sources proposed the use of linear optimization model based on linear response matrix approach [3] and statistical pattern recognition [4] .
Heuristic optimization techniques such as Genetic Algorithm (GA) and Simulated Annealing are efficient in solving such complex, non-linear, inverse problems having non-unique solutions. Estimates of the unknown model parameters and source characteristics [5] ; minimizing the square of the normalised residual error using embedded nonlinear optimization technique for source identification [1] , [6] and [7] ; Genetic Algorithm (GA) based optimization approach minimizing the square of the residual error [8] -[10] . Artificial Neural Network (ANN) approach [11] -[13] ; constrained robust least square approach [14] and [15] ; classical optimization based approach [16] -[18] ; Simulated Annealing (SA) as optimization for source identification [19] [20] . A review of different optimization techniques for solving source identification problem is presented in [21] and [22] .
Objective functions for solving unknown groundwater pollution source identification are complex multivariate optimization problems. Such formulations are highly non-linear containing several local and global optima. In identification of unknown pollution sources, the stress so far has been on applying different, more robust and advanced optimization algorithms for accurate identification. In the quest for search of a global optimum solution, this study takes a look at the objective function formulations, and how different formulations of the same objective can affect the accuracy of the solution using the same optimization algorithm. This is demonstrated by comparing two different sets of objective function formulation for identification of unknown pollutant sources using SA as the optimization algorithm.
All source identification methods rely on the observed concentration measurements, taken from a few sparse observation locations at discrete time steps over a monitoring time horizon. Forward simulation of the flow and transport process is run using candidate values of the unknown source flux release pattern to predict the pollutant concentration at observation locations. The observed pollutant concentration measurements are compared to that of simulated pollutant concentration measurements for optimal source identification. A close match between the observed and the simulated concentration essentially means near accurate simulation of the actual pollution scenario. Thus, the main objective of optimization based methodology for identification of unknown pollution sources is to minimize the difference between the observed pollutant concentration measurements and simulated pollutant concentration measurements over all the observation locations, taken at discrete time steps over a monitoring time horizon. The defined mathematical function representing this general objective is the objective function. Different researchers have used different mathematical formulation for writing the objective function. However, not all mathematical formulations for the same objective function yield the same result.
The main aim of this study is to compare two different mathematical formulations for the general objective of minimizing the difference between the simulated and the observed concentration measurements in a linked simulation-optimization model. The flow and contaminant transport simulation models are utilized for simulating the aquifer responses to different candidate solutions of the source identification model. The two mathematical formulations of the objective function i.e. minimizing the absolute difference between the observed and simulated pollutant concentration measurements and minimizing the square of the normalised difference between the observed and simulated pollutant concentration measurements are evaluated for their accuracy of the identification result and efficiency of the model. The source flux release history is considered as the only explicit unknown decision variable in this study.
2. Methodology
The proposed methodology uses a linked simulation-optimization for source identification where the source flux release history is the only explicit unknown variable in the optimization model. Two separate mathematical formulations of the form 1)  and 2)
and 2)  are used as objective function to solve the optimal source identification model. SA is used for solving the optimization problem with an objective of minimizing the difference between the simulated and measured pollutant concentrations measurements at the observed locations. The unknown source fluxes release history is obtained as direct solutions of the source identification model.
are used as objective function to solve the optimal source identification model. SA is used for solving the optimization problem with an objective of minimizing the difference between the simulated and measured pollutant concentrations measurements at the observed locations. The unknown source fluxes release history is obtained as direct solutions of the source identification model.
2.1. Linked Simulation-Optimization Model
Optimal source identification requires accurate identification of the release history of unknown pollution sources. This requires the use of simulation models to simulate the response of the groundwater system to any specified pollution source scenario. This is achieved by using a linked simulation-optimization approach. Linked simulation optimization model simulates the physical process of flow and solute transport within the optimization model. The flow and solute transport simulation models are treated as important binding constraint for the optimization model. Therefore any feasible solution of the optimization model needs to satisfy the flow and the transport simulation model. The advantage of this approach is that, it is possible to link any complex numerical model to the optimization model when using this approach. In this optimal source flux identification model, the flow and transport simulation models are linked to the optimization model using the SA algorithm for solution.
2.1.1. Groundwater Flow Simulation Model
A three dimensional numerical model MODFLOW [23] is used to simulate the groundwater flow in the polluted aquifer. MODFLOW is a computer program that numerically solves the three-dimensional groundwater flow equation for a porous medium by using a finite-difference method. The partial differential equation for groundwater flow [24] is given by Equation (1):
 (1)
(1)
where Kxx, Kyy and Kzz represent the values of hydraulic conductivity along the x, y and z axes (L∙T−1);
h is the potentiometric head (L);
W is the volumetric flux per unit volume representing sources and/or sinks (T−1);
Ss is the specific storage of the porous material (L−1);
t is time (T);
x, y and z are the cartesian co-ordinates (L).
2.1.2. Solute Transport Model in Groundwater System
A three dimensional modular pollutant transport model MT3DMS [25] is used to simulate the solute transport in the polluted aquifer system. The transport model (MT3DMS) utilizes the flow field generated by the flow model (MODFLOW) to compute the pollutant plume. The partial differential equation describing three-dimensional transport of pollutants in groundwater [26] is given by Equation (2).
 (2)
(2)
where C is the concentration of pollutants dissolved in groundwater (M∙L−3);
t is time (T);
xi is the distance along the respective Cartesian coordinate axis (L);
Dij is the hydrodynamic dispersion coefficient tensor (L2∙T−1);
vi is the seepage or linear pore water velocity (L∙T−1); it it is related to the specific discharge or Darcy flux through the relationship, vi = qi/θ;
qs is volumetric flux of water per unit volume of aquifer representing fluid sources (positive) and sinks (negative) (T−1) ;
Cs is the concentration of the sources or sinks (M∙L−3);
θ is the porosity of the porous medium (dimension less);
 is chemical reaction term for each of the N species considered (ML−3∙T−1).
is chemical reaction term for each of the N species considered (ML−3∙T−1).
2.1.3. Optimization Model
SA is used as an optimization algorithm to solve the optimization problem. Simulated annealing is a meta-heuristic search algorithm capable of escaping from local optima. Its use of hill-climbing moves to escape local optima makes SA efficient in solving non-convex optimization problems. Its ease of implementation of complex objective functions, and likely convergence to a global optimal solution enhances its suitability for solving ill-posed inverse problems, as is the case with unknown groundwater pollution source characterization. SA, first introduced by [27] , is an extension of the Metropolis Algorithm [28] . The basic concept of SA is derived from thermodynamics. Each step of SA algorithm replaces the current solution by a random nearby solution, chosen with a probability that depends on the difference between the corresponding function values and algorithm control parameters (initial temperature, temperature reduction factor etc.). In this study, SIMANN a FORTRAN public domain code for SA developed by [29] is utilized for the solution algorithm.
2.1.4. Source Flux Identification Model
In source identification problem where the starting time of the activity of the sources is known, temporal pollutant source fluxes from all the potential sources, represented by the term  in the transport Equation (2) are the only explicit decision variable. Source flux identification using linked simulation-optimization is solved by minimizing the difference between the simulated pollutant concentration measurements and the observed pollutant concentration measurements in space and time. The solution strategy is to generate candidate values of these unknown variables within the optimizations algorithm, use these values for forward simulations of flow and transport models, compute the difference between simulated and observed pollutant concentrations and finally obtain an optimal solution that minimizes the difference between observed and simulated values. In the optimal source flux identification model two separate mathematical formulations of objective function is used given by Equations (3) and (4), respectively.
in the transport Equation (2) are the only explicit decision variable. Source flux identification using linked simulation-optimization is solved by minimizing the difference between the simulated pollutant concentration measurements and the observed pollutant concentration measurements in space and time. The solution strategy is to generate candidate values of these unknown variables within the optimizations algorithm, use these values for forward simulations of flow and transport models, compute the difference between simulated and observed pollutant concentrations and finally obtain an optimal solution that minimizes the difference between observed and simulated values. In the optimal source flux identification model two separate mathematical formulations of objective function is used given by Equations (3) and (4), respectively.
 (3)
(3)
 (4)
(4)
Subject to
 (5)
(5)
 represents the simulated concentration obtained from the transport simulation model at an observation location at time t and for a specific source flux
represents the simulated concentration obtained from the transport simulation model at an observation location at time t and for a specific source flux . This constraint essentially represents the linking of the optimization algorithm with the numerical groundwater flow and transport simulation model through the decision variables.
. This constraint essentially represents the linking of the optimization algorithm with the numerical groundwater flow and transport simulation model through the decision variables.
where
 = observed concentration measurement at observation location iob at time t(M∙L−3);
= observed concentration measurement at observation location iob at time t(M∙L−3);
 = corresponding estimated concentration at observation location iob at time t(M∙L−3);
= corresponding estimated concentration at observation location iob at time t(M∙L−3);
NOB = total number of monitoring locations;
N = is the total number of monitoring time steps at location iob;
δ = is a constant specified e.g. any number between 1 to 1000;
Abs = is the absolute difference.
The first objective function formulation shown by Equation (3) calculates the difference between the simulated pollutant concentration and observed pollutant concentration in the numerator. This difference is divided by the observed pollutant concentration plus a specified constant value δ. The objective of adding a small constant term is to avoid any indeterminate case when the value of observed pollutant concentration is zero. However, the value of the constant δ can significantly impact the outcome of the optimization and hence should be chosen judiciously. The whole term is squared so that the negative and the positive errors do not cancel out each other. The second objective function formulation (Equation (4)) defines the simple difference between the simulated pollutant concentration and observed pollutant concentration. The absolute difference is considered for minimization to avoid cancelling of the negative and the positive errors. These two objective functions are chosen to demonstrate the effect of different objective function formulations for the same general objective of optimization.
3. Performance Evaluation of Developed Methodology
To evaluate the performance of the two different objective function formulations for accurate identification of the pollution source fluxes using linked simulation-optimization, a hypothetical homogeneous, isotropic, and saturated aquifer is utilized as an illustrative example as shown in Figure 1. Cells marked with red star represent the grid locations containing a potential pollutant source S(i) where I represents the source number. Cells marked with green circle are the grid locations containing a monitoring well. Groundwater flow and solute transport model is simulated with hydro-geological parameters as given in Table1 The synthetic concentration measurement data used for the specified polluted aquifer facilitates evaluation of the methodology without having to account for the unknown reliability of any field data.

Table 1. Hydro-geological parameters for study area.
3.1. Determining Ideal Value of Constant “δ” in the First Objective Function Formulation
The accuracy of the source flux identification result is sensitive to the formulation of the objective function. Hence the effect of δ is analysed for the first objective function formulation. To determine an suitable value of δ to be used in the formulation of objective function, different values of the constant δ are utilized 1, 10, 100 and 1000, respectively. The source flux identification model is solved using first objective function formulation (Equation (3)). The value of δ is varied every time to find the most suitable value of δ out of 1, 10, 100 and 1000.The polluted aquifer study area is assumed to have 4 potential pollutant source locations, of which source three S3 is a dummy (not actual) source. The activity duration of the sources is divided into three equal stress periods of 500days each and the pollutant flux from each of the sources is assumed to be constant over a given stress period. The pollutant flux from each of the sources is represented as S(i)(j), where i represents the source number and j represents the stress period number. A total of twelve source fluxes S11, S12, S13, S21, S22, S23, S31, S32, S33, S41, S42 and S43 are considered as explicit unknown variables in the source flux identification model.
3.2. Comparing the Objective Function Formulation
Once a suitable value of δ is determined, nine different scenarios of source flux identification is solved using the determined ideal value of δ in the first objective function formulation (Equation (3)). These scenarios vary in terms of the observation well locations for which concentration measurements are used for identification of unknown source fluxes. The same scenarios are then solved using the second objective function formulation (Equation (4)) to compare the accuracy of source flux identification using the two formulations. All scenarios used for comparing the accuracy of source flux identification using the two formulations comprise of three actual sources and no dummy source is present. This was to reduce the running time of the optimization model for repeated performance evaluation runs. The activity duration of the sources is divided into three equal stress periods of 500days each and the pollutant flux from each of the sources is assumed to be constant over a stress period. The pollutant flux from each of the sources is represented as S(i)(j), where i represents the source number and j represents the stress period number. A total of nine source fluxes S11, S12, S13, S21, S22, S23, S31, S32, and S33are considered as explicit unknown variables in the source flux identification model.
In all nine scenarios a total of four temporal pollutant concentration measurements from each of the six observation wells are utilized. In all the scenarios the observation well location varies and is randomly chosen from the 33 potential monitoring well locations shown in Figure 1. Groundwater flow is assumed to be steady state. For evaluation purpose, the observed aquifer responses at the observation locations are simulated by solving MODFLOW (Equation (1)) and MT3DMS (Equation (2)) in GMS 7.0, along with appropriate groundwater aquifer initial and boundary conditions. The resulting concentrations are then perturbed to represent the effect of random measurement errors. These perturbed concentration values are obtained by incorporating random measurement errors with maximum deviation of 10 percent as shown in Equation (6).
 (6)
(6)
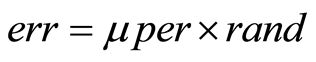 (7)
(7)
where
 is the perturbed numerically simulated concentration value;
is the perturbed numerically simulated concentration value;
 is the numerically simulated concentration value;
is the numerically simulated concentration value;
 is the error term;
is the error term;
 is the maximum deviation expressed as a percentage;
is the maximum deviation expressed as a percentage;
 is a random fraction between −1 and +1 generated using Latin hypercube distribution.
is a random fraction between −1 and +1 generated using Latin hypercube distribution.
In all the scenarios, source fluxes are estimated by first assuming error free data, and then estimated using erroneous concentration measurements with random error.
4. Results and Discussion
The solution results of pollution source flux identification for determining the most ideal value of δ is presented in Figures 2-5. The source flux identification model is solved using first objective function formulation (Equation (3)). Each of the unknown source flux variables (S11, S12, S13, S21, S22, S23, S31, S32, S33, S41, S42 and S43) is marked on the x axis having 6 corresponding bars. The first bar is the actual value of the source flux. The second bar represents the estimated flux value using the second objective function formulation (Equation (4)).The third bar to the sixth bar represent the estimated source flux value when using constant value δ in Equation (3) as 1, 10, 100, and 1000, respectively in the first objective function formulation. The source flux identification model solved using error free concentration measurement data is shown in Figure 2. The error of estimation of the source flux values is given by the absolute difference between the actual source flux value and the estimated source flux values shown in Figure 3.

Figure 2. Source flux identification result for different values of δ using error free concentration measurements.

Figure 3. Source flux estimation error for different values of δ using error free concentration measurements.
The source flux identification model solved using concentration measurement data with random error is shown in Figure 4. The error of estimation of the source flux values while using erroneous concentration measurements is shown in Figure 5.
It is evident from these results that the most suitable value of δ amongst 1, 10, 100 and 1000 to be used in the first objective function formulation (Equation (3)) is 1. The estimated source flux values for δ = 1 gives the least error in the estimation of the source fluxes both for error free data and erroneous data. Even the dummy source S3 is well identified when using δ = 1in case of error free data. While using erroneous concentration measurements with random error, the source flux identification results show large errors of estimation as compared to those obtained utilizing error free data. The estimated source flux value for source flux S11 show large error of estimation for all the values of δ. This general trend in case of S11 may be attributed to the observed concentration measurements data used in the identification model. Not all observation well locations are optimally located for source flux identification. Concentration measurements from these non-optimally located observation wells may not be efficient in accurate source flux identification [30] . Also the perturbed error term which were randomly distributed across all observed concentration measurements may non-uniformly impact some observations more than the others. This can easily result in an incorrect estimation of the source fluxes. The same explanation is also plausible in case of S32 while using the value of δ = 1. Otherwise these may be regarded as an exception.
Comparing the source flux identification results for the first objective function formulation (Equation (3)) while using the value of δ as 1and the second objective function formulation (Equation (4)) do not show large difference in the accuracy of the estimated flux values. This is true both in case of error free and erroneous concentration measurements. In order to get a clear idea as to which of the two formulation work better in case of source flux identification, 9 different scenarios of source flux identification are solved. Source fluxes are estimated for all the nine scenarios using both the objective function formulations. The value of the constant δ is kept as 1 in all the cases. These identification results for all the nine scenarios using error free concentration measurement data and erroneous concentration measurement data is shown in Figures 6-14. Each of the unknown source flux variables (S11, S12, S13, S21, S22, S23, S31, S32 and S33) is marked on the x axis having five corresponding bars. The first bar is the actual value. The second and third bar represents the estimated values using error free concentration measurements, respectively. The fourth and the fifth bar represent the estimated values using erroneous concentration measurements.
It is evident from these solution results that the source flux identification are more accurate while using the first objective function formulation (Equation (3)). However, there is one or two odd instances where few of the source fluxes are better identified by using the second objective function formulation (Equation (4)). The solution results for source flux estimates using erroneous concentration measurements data show large errors of estimation in comparison to error free measurement data. These deviations between the actual and the estimated

Figure 4. Source flux identification result for different values of δ using erroneous concentration measurements.

Figure 5. Source flux estimation error for different values of δ using erroneous concentration measurements.

Figure 6. Source flux identification results for Scenario 1.

Figure 7. Source flux identification results for Scenario 2.

Figure 8. Source flux identification results for Scenario 3.

Figure 9. Source flux identification results for Scenario 4.

Figure 10. Source flux identification results for Scenario 5.

Figure 11. Source flux identification results for Scenario 6.

Figure 12. Source flux identification results for Scenario 7.

Figure 13. Source flux identification results for Scenario 8.

Figure 14. Source flux identification results for Scenario 9.
value of the source fluxes show the effect of errors in concentration measurement data, which accounts for random measurement errors in a real world scenario.
It is interesting to note that though both the objective function formulations are practically of the same general nature, i.e. to minimize the difference between the simulated response of the aquifer and the actual response of the aquifer, there is contrasting difference in the accuracy achieved by both the formulations while using identical optimization algorithm for solution. Although this difference may not be so pronounced when using error free concentration measurements, it is more apparent when erroneous measurements are utilized. This can be explained by analysing the two objective formulations. If we imagine the solution response space representing the objective function values for corresponding decision variable values as a rough plane, such that roughness of the surface creates multiple local optima, the objective is to find the global optimum amongst these local optima. The second objective formulation which uses the absolute difference between the observed and the estimated pollutant concentration value do not alter the roughness of the search space at all. However, when the difference between the observed and the simulated pollutant concentration is divided by the observed pollutant concentration measurement, the difference gets normalised. This gives proportional weight age to pollutant concentration measurements for all the observation locations at all times. As a result there is greater distinction between different local optima and it is easier for the optimization algorithm to get out of any local optima. The biggest challenge of any optimization algorithm is to get out of local optima and find a global optimum.
In order to illustrate this difference due to different objective function formulation, the objective function solution space is plotted for different objective function formulations over the search domain (Figure 15). Most complex optimization problems are multi-multivariate in nature. Since it is not possible to plot N-dimension solution space hence, the solution space is plotted for a two dimensional problem. Four different formulations are considered to see the variation in the solution space contour 1) ; 2)
; 2)
 ; 3)
; 3)  and 4)
and 4) . Figure 15 shows a three dimensional plot of the solution space plotted in the decision variable space. The plots starting from the top left, in the clockwise direction shows the solution space surface for objective function formulations (1) to (4), respectively.
. Figure 15 shows a three dimensional plot of the solution space plotted in the decision variable space. The plots starting from the top left, in the clockwise direction shows the solution space surface for objective function formulations (1) to (4), respectively.

Figure 15. Surface plot of solution space for different objective function formulations (1) to (4).
It can be seen in these surface plots that the roughness in the solution space surfaces are not same in all the case. It can be seen that in case of objective function formulation (1), the peaks and the trough in the solution surface profile are more distinct as compared to the others. Since it is difficult to compare these surface plots, the contours for the same are plotted as shown in Figure 16. These plots starting from the top left, in the clockwise direction shows the solution space contours for objective function formulations (1) to (4), respectively. These contours show the spatial density of the peaks as well as the contrast between the low values and high values in the objective function solution space. In case of objective function formulation (1), it appears that the contours are able to identify the peaks and the troughs with a greater contrast as compared to formulation (2). This can result quicker move of the search algorithm from one peak/trough to the other. Therefore the objective function used in this study which is which is similar to formulation (1), is advantageous. In case of objective function 3 and 4, the entire space is dominated by a low value range or a high value range with comparatively greater uniformity. In case of objective function formulation (4), the peaks get more prominent but at the cost of the troughs which get diminished in comparison to the peak values. Vice versa occurs in the objective function formulation (3). Since the global optimum solution lies in one of these peaks/troughs, it is important to ensure that the search algorithm looks for the optimum solution in these peaks/troughs and still can easily come out of the local optimal ones. A solution space having distinct peaks and the troughs can facilitate the search algorithm to investigate these peaks/troughs, and easily come out of local optima.

Figure 16. Contour plot of solution space for different objective function formulations (1) to (4).
Figure 17 shows the contour plot of the objective function solution space for the two formulations (1) and (2) plotted against the difference between the estimated value and the observed value. It can be seen that for a unit change in the difference between the estimated value and the observed value the change in the objective function value is steep in the second formulation. The first formulation provides for a large area around the optimum solution. Steep gradient may be useful if using the classical gradient search methods, but such a scenario may result in missing the optimum solution in a heuristicrandom search using SA. However, a larger exposed surface around the global optimum solution can improves the chance of finding the optimum using a heuristic random search algorithm like SA. Therefore there is a better accuracy in source identification using the first objective function formulation as compared to the second objective function formulation.
One more reason for having the constant δ incorporated in the objective function is to avoid any indeterminate objective function value when observed value is zero. The value of the constant δ should be of the same order as the observed values so that the normalization does not get skewed due to very large value of the constant δ. Very small values of the constant δ may again lead to indeterminate values when the observed value becomes zero.
5. Summary and Conclusions
From the performance evaluation results it is clear, that different mathematical formulations of the same general objective result in different degree of accuracy in the source flux identification. The objective function, in which the square of the normalised difference is minimized, performs better than the absolute difference in estimating the source flux values. However, while normalising the difference between the observed and the simulated concentration measurements, the value of the constant δ added to the observed concentration measurement should be of the same order as observed concentration values. Though the advantage of using such normalization may not be apparent when using error free data, it becomes clear when the observed values are perturbed with random error term. Normalization gives proportional weight age to observed concentration measurements from all the observation points, which otherwise gets over shadowed due to the presence of few large values of observed concentration measurements in the defined objective function. Normalization also smooths the effect of the random errors in the observed values. This seems to result in more accurate source flux identification.
Although it is important to use a robust optimization algorithm for finding the global optimum, the role of the objective function formulation cannot be overlooked. This study presents a perspective of the optimization problem in which the role of the mathematical formulation of the objective function is encapsulated in terms of the roughness features in a multi-dimensional, complex non-linear multi-variate objective function solution space. These features may determine the ability to identify a global optimum. This study presents comparison of two mathematical formulations, though other formulations can be tested for suitability. A proper mathematical formulation in conjunction with a robust optimization algorithm can facilitate the search for a global optimal solution. This study throws some light on the choice of proper objective function for obtaining a global optimal solution.

Figure 17. Contour plot of solution spacevs. Difference between observed and simulated values for objective function formulations (1) and (2).
Acknowledgements
We authors would like to thank Cooperative Research Centre for Contaminant Assessment and Remediation of the Environment and James Cook University, Australia for partial funding and support for this research.
NOTES
*Corresponding author.