1. Introduction
Quantum mechanics arises from the long and successful efforts of scientists to explain experimental phenomena such as the radiation law and the photoelectric effect, for which cannot account classical mechanics. Classical physics always represents our world in the relatively graphical and intuitive terms, greatly different from quantum physics, which is strong on mathematical rigor but light on physical intuition. The quantum properties of microscopic matter imply a renunciation of the possibility of their being understood in the customary imaginative sense, which is difficult to be admitted or embarrassed to be accepted for some classical physicists. The discussions about the principle of nonlocality of the material particles have never been stopped since quantum theory was developed in the 1920s [1] [2] . The argument relates mainly to two queries: uncertainty principle and probabilistic interpretation of wave functions. In the following we will review both issues in turn, and the first is uncertainty principle. All we should do is to provide added evidence and derivation for those remain far from clear in Copenhagen interpretation, and then make it further complete.
In general, a prevailing perception from our daily experience is that the laws of physics should be completely objective, and they should not depend in any way on what dimensions and mass of a moving object has. Namely, there should be uniform laws of physics to describe moving objects within a common frame of reference. Einstein suggested that the particle’s motion should be deterministic and realistic like classical objects rather than probabilistic. Copenhagen interpretation is regarded as anti-realistic because Einstein’s constant researching and sever criticism. Here we first think of an example of the interrelation between Newton’s mechanism and Einstein’s special theory of relativity. The physics of Newton provides an ultimate inertial frame of reference with both absolute space and time, in which all motion could be in principle measured accurately. Einstein’s special theory of relativity revised Newton’s point of view and gave us new concepts—there are only relativistic space and time but absolute ones. Lorentz transformation can be simplified into Galiliean transformation only if an object’s velocity is far smaller than light speed, which leads to the fact that an absolute space and an absolute time come true. Some authors mentioned without rigorous proof that the dimensions and mass of a macroscopic object are too great to consider uncertainty principle, that is, Plank’s constant is assigned as zero, and then the object’s motions are to be thought of as deterministic [3] . An essential problem is whether or not the uncertainty principle is intrinsically applicable to classical physics, whatever the dimensions and masses. If the principle satisfies classical physics, up to now, why cannot we get a derivation of the principle starting from the laws of classical physics? How should we derive the principle without the means of quantum mechanics if the principle is an objectively general law? So far, we have known that the noncommuting properties of the operators of observables result in uncertainty relations, and these operators only exist in a complex space where the wave equation of quantum mechanics works. In contrast, the object’s motion only undergoes in a real space where classical physics works. For this reason, the uncertainty principle is usually viewed as a crucial base for quantum mechanics rather than classical physics. In a practical sense, we can say there is no uncertainty principle and there is no probabilistic interpretation. In Einstein’s opinion it seems that a moving object in a real space does not obey the principle unless the principle is an attribute of the real space rather than a purely algebraic description of nature [4] . We think that there are no space and time, there are no physical laws. We should not ignore the properties of the space and time, which directly affect our observation and knowledge on nature. In the second section of this paper we will prove that uncertainty relation is an intrinsic attribute of a real space independent of any moving object such that the uncertainty principle is available to all objects, no matter what dimensions and masses they will have. Classical physics is only a peculiar consequence of the elimination of these attributes, like Newton’s physics is a result of neglecting the relativistic effect. As a result, quantum formalism is only taken as a good approximate description of microscopic particles rather than a real motion law. For example, the arrival of an electron at a detector in double-slit interference experiment can be rationally considered as one of our expecting events, just like there appeared to be a good weather sometimes on our prediction. Our derivation will also confirm a fact that there is not any evidence so far showing that the collapse of the wave functions is a real physical phenomenon.
We review the probabilistic interpretation in the following. Its kernel is the principle of nonlocality for the matter particles, which has been tested and verified by experiments supported by modern technique and devices. It is said that Bell’s inequality is a way to distinguish between quantum mechanics and classical mechanics for the behavior of particles such as photons. The results of the experiments using Bell’s inequality have now come down in favor of quantum mechanics [5] -[7] . In fact, it is impossible to show classical physics phenomenon for a quantum system, no matter what a kind of experiment is taken. Because when we make an experiment not only the quantum system but also the measuring apparatus are placed in a position-momentum space and a timeenergy space, both system and the apparatus are absolutely affected by the uncertainty principle belonging to the physical nature of these spaces. For this reason, Bell’s inequality is only an experiment showing once more the fundamental phenomena for quantum entities. Multiphoton experiments tests of quantum nonlocality show that Bell’s theorem is not sufficiently theoretical argument [8] [9] . Born’s probabilistic interpretation itself is pure guesswork but a result of theoretical evolution [10] . It is the guesswork that leads to occurrence of some alternatives to Copenhagen interpretation such as the ever popular “Many-world” interpretation of quantum mechanics, “Hidden-variable” theory, “Consistent-histories” interpretation, and “Decoherenc” mechanism [11] -[14] . Furthermore, there are a series of oppositional voice including the Einstein’s EPR paradox and the Schrödinger’s cat paradox, which directly blame Born’s interpretation [15] [16] . We think that there should be a theoretical proof for the nonlocality principle so as to decrease the disputation in the future. Born’s guesswork based on two facts: The first is Heisenberg uncertainty principle; the second is an idea of Einstein’s interpreting the square of the optical amplitudes as probability density for the occurrence of photons. In our opinion, the wave-particle duality of light is most helpful in visualizing the nature of the duality, which directly leads to their probabilistic distribution. It is clear that there is no photon concept prior to Plank’s quantum theory and Einstein’s photoelectric effect approach. In a homogeneous medium a free electromagnetic field also is called radiation field due to free of charges and currents, and shows a wave character that is called light wave, and the wave functions are just the field’s vector potential. The field energies are discretized by Plank’s theory, corresponding to quanta called photons by Einstein. Dirac first recognized that the dynamical properties of light wave functions are equivalent to the dynamical ones of a set of oscillators; they are just the same one looked at from two different points of view. One oscillator associated with each independent wave function state, which enables a function of the wave and corpuscular theories of light to be effected [17] . Therefore, we can say the radiation field is characterized by the simply harmonic wave, and the wave quantization results in photons. Two types of particles similar to photons from the quantization are phonons and magnons in solid state physics; the former results from the lattice wave quantization, and the latter are the products of the spin wave quantization [18] . It should be emphasized that there is no wave and there is no the relevant quantization. Alternatively, the quantization of a temperature field is not physically accepted. Hence, the terms of the wave quantization have more definite meaning than the terms of the field quantization. In contrast with the fact that Maxwell’s field equation is prior to the photon concept, the electron concept is prior to Schrödinger wave equation. Schrödinger imagined an electron as a wave with zero wavelength, obeying Hamilton’s principle, and the wave was directly influenced only by its immediate surroundings [19] . In order to make the energies discrete, he treated the Hamiltonian as an operator, and the relevant energies are amenable to Plank theory. Meanwhile, the wave functions determined by his equation turn into the eigenvector in complex space. Before further discussion about the wave-particle duality it is of enlightening meaning to reassert the concept of electric energy. Electric potential energy accounts for work on an electron done by electric force and gives added insight regarding energy and energy transformation without the necessity of dealing with the force directly. The energy does not belong to the electron alone, but both the electron and the electric field. For Schrödinger equation, it is an inappropriate perspective to separate the electron from the Hamiltonian and assign the energies only to the electron, regardless of the electric field. A space consisting of electron and electric field is different from vacuum, and such a space may be called a field. As such, it is the space (or the field) rather than the electron exhibits a wave phenomenon. The wave like light wave can be made quantization to give particles, none of which is the electron that is a material particle. It can be understood since de Broglie’s work antedated Schrödinger equation and Dirac radiation field theory, and his postulate was not able to ascribe the wave properties to the space containing electrons. It is the continuous motion of the electron that causes the wave. It seems that Schrödinger did not perceive that the wave originates in the electron’s motion, and the wave functions can change with time even if for a steady system. The wave motion requires each wave function to vibrate at its own site. The wave hence is a disturbance of the wave functions in the space. A wave function at a position transfers its physical state in this way to the wave function at the next position. The wave as a whole is to be made quantization to produce particles to be like photons. Even though Schrödinger equation for single electron gives perfectly accurate solution, there is still more or less deficiency of dynamical characteristics for the wave functions. His time-dependent wave equation is a second-order differential in the three spatial coordinates but only a first-order differential in time. Actually, the wave motion is a classical phenomenon satisfying a classical dynamical equation with a second-order differential in time. In addition, the wave function of a system of N electrons is a function in a 3N-dimensional configuration space, in which the Born’s probabilistic interpretation cannot be used. It is difficult to imagine that a physical reality exists in such an abstract multidimensional configuration space. The double-slit experiment is a successful example of the probabilistic interpretation [14] [20] . The behavior of an electron in the space between the slit and the detector shows the characteristics of a free electron. For these reasons, in the third section of this paper, the wave functions for the space involving a free electron are obtained by means of a dynamical equation. Then, the wave quantization for such space will be made, which will give a theoretical evidence of the probabilistic interpretation. In the fourth section we discuss different meanings of wave-particles for photons and for electron. The relativistic effect will not be discussed in this paper.
2. Uncertainty Relations as Attributes of Spaces
In a 3-dimensional flat real space of coordinates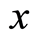 ,
,  , and
, and 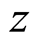 there is a cotangent space with its natural bases,
there is a cotangent space with its natural bases, 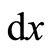 ,
, 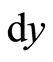 , and
, and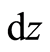 , together with which there is a tangent space with natural bases
, together with which there is a tangent space with natural bases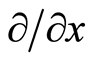 ,
, 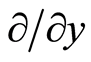 , and
, and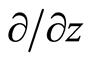 . The two vector spaces are dual to each other in terms of mathematics, and their dual bases obey the following formula [21] :
. The two vector spaces are dual to each other in terms of mathematics, and their dual bases obey the following formula [21] :
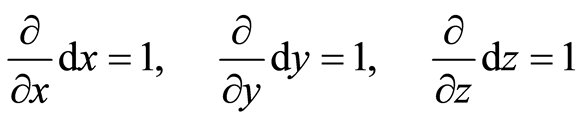 (1)
(1)
where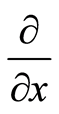 ,
, 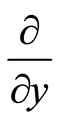 , and
, and 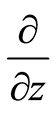 are also known as partial differential operators. Equation (1) is a restriction relation between dual bases. Suppose that there is a linear momentum space with its bases
are also known as partial differential operators. Equation (1) is a restriction relation between dual bases. Suppose that there is a linear momentum space with its bases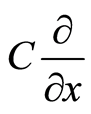 ,
, 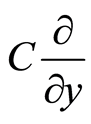 , and
, and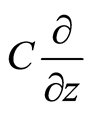 , where
, where 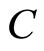 is a proportional constant and makes these bases have a momentum dimension. In physical sense,
is a proportional constant and makes these bases have a momentum dimension. In physical sense, 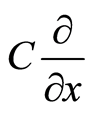 is parallel to
is parallel to 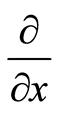 because a velocity associated with
because a velocity associated with 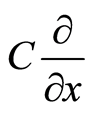 is along the tangent direction. At the same time,
is along the tangent direction. At the same time, 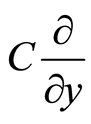 and
and 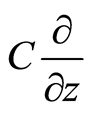 are parallel to
are parallel to 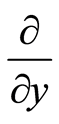 and
and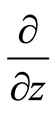 , respectively. From Equation (1), we get further
, respectively. From Equation (1), we get further
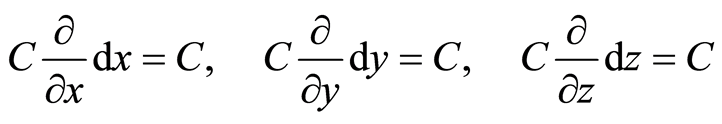 (2)
(2)
According to differential geometry [21] , a complex structure on a vector space tantamount to multiplying the basis of the vector space by an imaginary number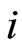 , which represents the square root of
, which represents the square root of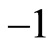 . Such procedure is called map in mathematics sense. Thus, a complex basis corresponding to
. Such procedure is called map in mathematics sense. Thus, a complex basis corresponding to 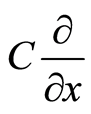 is
is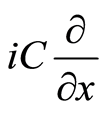 , which complex conjugational basis is
, which complex conjugational basis is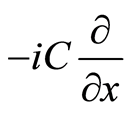 . Compared with the momentum operator
. Compared with the momentum operator 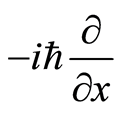 of quantum mechanics, we right now understand the constant
of quantum mechanics, we right now understand the constant 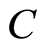 does be Plank’s constant due to the map is one-to-one. Equation (2) then becomes
does be Plank’s constant due to the map is one-to-one. Equation (2) then becomes
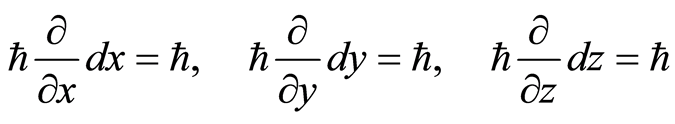 (3)
(3)
A natural basis of a vector space is different from a unit vector. There is no a specific length definition for a natural basis in mathematics, its length is uncertain. In the special theory of relativity the length of a basis 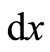 is considered as a distance or an interval, represented as
is considered as a distance or an interval, represented as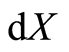 , and
, and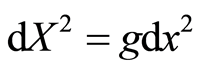 , where
, where 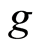 is Riemannian metric [22] . In a region where Galilea transformation is valid the Riemannian metric equals to a unit of length. In terms of mathematics, the length of
is Riemannian metric [22] . In a region where Galilea transformation is valid the Riemannian metric equals to a unit of length. In terms of mathematics, the length of 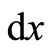 can be written as
can be written as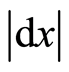 , which is its module, so
, which is its module, so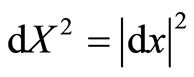 . The
. The 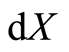
is a measurable quantity equivalent to 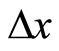 of quantum mechanics. We then have
of quantum mechanics. We then have
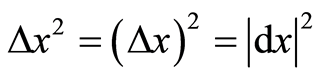 (4)
(4)
Likewise,
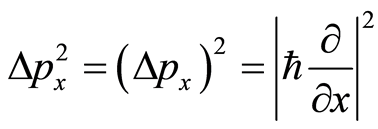 (5)
(5)
Using Equations (3)-(5), we get
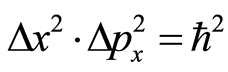 (6)
(6)
Clearly, we do not know the individual values of 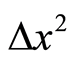 and
and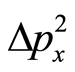 , except their mutual restricting relation Equation (6). We can consider the lengths of the bases at a particular point
, except their mutual restricting relation Equation (6). We can consider the lengths of the bases at a particular point 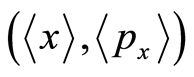 in a 2-dimensional position-momentum space (called a phase space in statistical mechanics), where
in a 2-dimensional position-momentum space (called a phase space in statistical mechanics), where 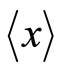 and
and 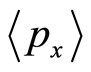 are statistical average values of
are statistical average values of 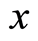 and
and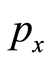 , respectively. The starting point of the basis
, respectively. The starting point of the basis 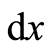 positions at the
positions at the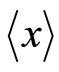 , and its end point arrives at the
, and its end point arrives at the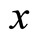 , and the length is
, and the length is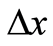 . The basis
. The basis 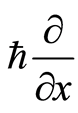 starts from the
starts from the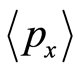 , and ends at the
, and ends at the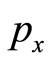 , its length is
, its length is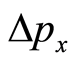 . In a measurable sense,
. In a measurable sense, 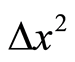 and
and 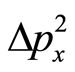 can be expressed by
can be expressed by
 (7)
(7)
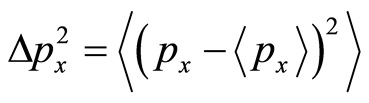 (8)
(8)
where the symbol 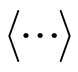 represents making average calculation. Equations (6)-(8) manifest uncertainty relation about position and momentum. With the same reason, we can get other uncertainty relations about
represents making average calculation. Equations (6)-(8) manifest uncertainty relation about position and momentum. With the same reason, we can get other uncertainty relations about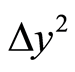 ,
, 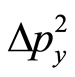 ,
, 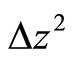 , and
, and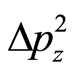 . The above derivation is as simple as the Heisenberg’s derivation in quantum mechanics.
. The above derivation is as simple as the Heisenberg’s derivation in quantum mechanics.
Although the time-energy uncertainty relation is consistent with experiment, it is not derived from the noncommuting property of relative operators since there is no time operator in quantum theory. We think that this relation should be an intrinsic attribute for the time-energy space. When mentioned the space-time Feynman pointed out [23] : “We have discovered four quantities which transform like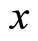 ,
, 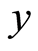 ,
, 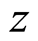 , and
, and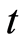 , and which we call the four-vector-momentum, …, it can be represented on a space-time diagram of a moving particle as an “arrow” tangent to the path. This is an arrow has a time component equal to the energy”. According Feynman, energy and time are dual to each other. At first, we get a dual relation for a cotangent basis
, and which we call the four-vector-momentum, …, it can be represented on a space-time diagram of a moving particle as an “arrow” tangent to the path. This is an arrow has a time component equal to the energy”. According Feynman, energy and time are dual to each other. At first, we get a dual relation for a cotangent basis 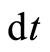 and tangent basis
and tangent basis 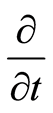 , and
, and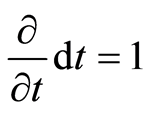 . An energy basis can be represented by
. An energy basis can be represented by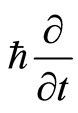 , which correspondingly mapping complex basis is
, which correspondingly mapping complex basis is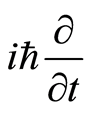 , called energy operator in terms of quantum mechanics. We then get
, called energy operator in terms of quantum mechanics. We then get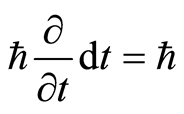 . At a point
. At a point 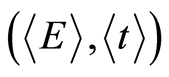 in a 2-dimensional time-energy space, we obtain the uncertainty relation:
in a 2-dimensional time-energy space, we obtain the uncertainty relation: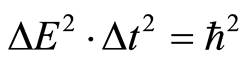 , where
, where
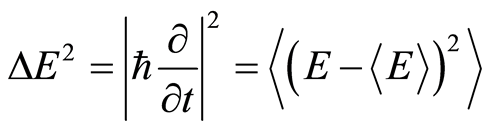 (9)
(9)
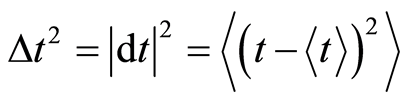 (10)
(10)
The relative Riemannian metric equals one unit length due to the flat space.
The above derivation indicates that uncertainty relations are really the attributes of the real space, but belongs to microscopic particles. When we want to describe an object’s motion, no matter whether the object is macroscopic or microscopic, we need to set up the space-time coordinate system in a reference frame, which means that the uncertainty relations are available for both classical physics and quantum physics, and affect a whole process of the motion. It is the intrinsic attributes that limit our ability to reach an underlying physical reality of the particles. Quantum mechanics is only an artificial description resulting from our perception of microscopic particles behavior. Just as Aage Petersen, Bohr’s assistant pointed out [3] : “There is no quantum world. There is an abstract quantum physical description. It is wrong to think that the test of physics is to find out how nature is. Physics concerns what we can say about nature.”
3. A Theoretical Evidence of Born’s Guesswork
We try to discuss a wave that propagates freely. Our demonstration starts in classical fashion of the wave available to Newton’s law. For brevity, we consider a case of one dimensional configuration space. The points on x-axis have the same nearest neighbor space denoted by a number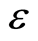 , which is sufficiently small but zero. Such division resembles the approach used in the path integral [24] , which mathematical significance is that the space is a metric space, in which two distinct points can always be surrounded by disjoint domains [25] . The identical interval is due to the space is homogeneous. A space contains only single free electron, and there is not any external force. As Kubo’s theorem states that the fluctuation in the space will decay [26] , but vanish due to uncertainty principle. Thus, the fluctuation force is weak. Let
, which is sufficiently small but zero. Such division resembles the approach used in the path integral [24] , which mathematical significance is that the space is a metric space, in which two distinct points can always be surrounded by disjoint domains [25] . The identical interval is due to the space is homogeneous. A space contains only single free electron, and there is not any external force. As Kubo’s theorem states that the fluctuation in the space will decay [26] , but vanish due to uncertainty principle. Thus, the fluctuation force is weak. Let 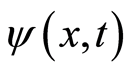 denote a wave function at position
denote a wave function at position 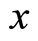 at time
at time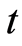 , the domain of
, the domain of 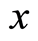 be
be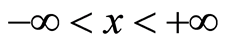 .
. 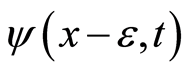 and
and 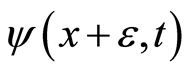 are the nearest neighbors of
are the nearest neighbors of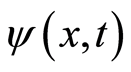 , respectively. We get
, respectively. We get
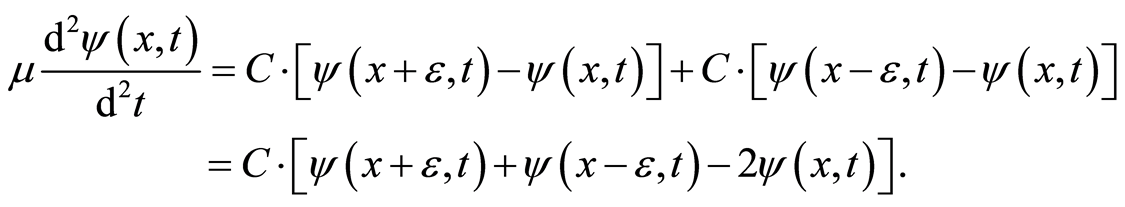 (11)
(11)
where 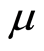 is equivalent mass and
is equivalent mass and 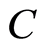 is a force constant. This is a difference equation in the deviation of wavefunctions, and the fluctuation force is linear in the deviation of the function values. The equation of motion is
is a force constant. This is a difference equation in the deviation of wavefunctions, and the fluctuation force is linear in the deviation of the function values. The equation of motion is
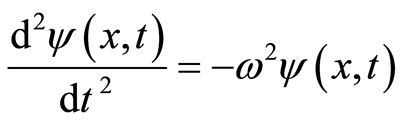 (12)
(12)
where angular frequency is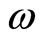 . By Equations (11) and (12), we have
. By Equations (11) and (12), we have
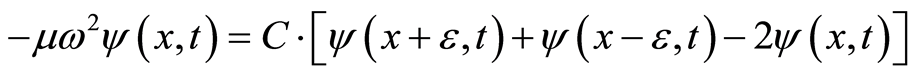 (13)
(13)
Equation (13) has a traveling-wave solution in the form
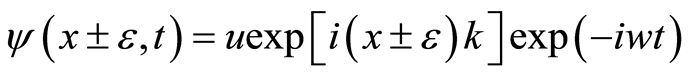 (14)
(14)
where 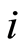 is imaginary, the
is imaginary, the 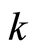 is wave vector,
is wave vector, 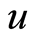 is a real constant. Inserting Equation (14) in Equation (13) yields
is a real constant. Inserting Equation (14) in Equation (13) yields
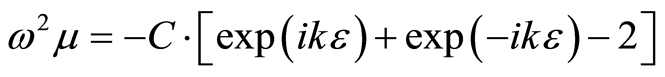 (15)
(15)
Using identity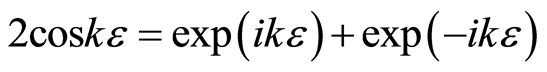 , we obtain a dispersion relation between
, we obtain a dispersion relation between  and
and 
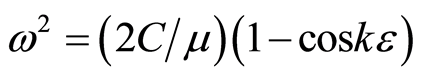 (16)
(16)
Since the frequency 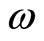 depends on the magnitude of the wave vector
depends on the magnitude of the wave vector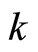 , it is rewritten as
, it is rewritten as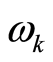 , and
, and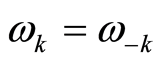 . The wave function then becomes
. The wave function then becomes 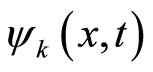 for a special mode
for a special mode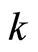 . The period of the function
. The period of the function 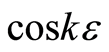 is determined by the total number
is determined by the total number 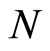 of possible vibration modes, and the range of underlying values of
of possible vibration modes, and the range of underlying values of 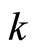 is specified by
is specified by
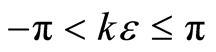 (17)
(17)
We put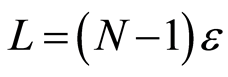 , which means that an identical mode repeatedly appears at the same time every propagating distance
, which means that an identical mode repeatedly appears at the same time every propagating distance 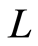 relative to a periodic boundary condition. The following discussion is limited to the region
relative to a periodic boundary condition. The following discussion is limited to the region 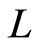 because of the periodic space. Therefore, the solution of Equation (12) is
because of the periodic space. Therefore, the solution of Equation (12) is
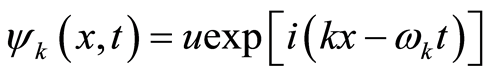 (18)
(18)
The de Broglie relation gives the momentum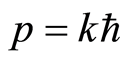 , inserting which in Equation (18), we get
, inserting which in Equation (18), we get
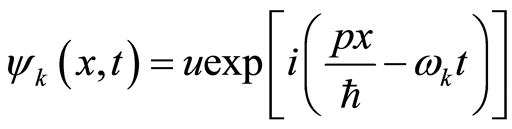 (19)
(19)
It is well known the wave function of an eigenvalue equation in the momentum representation for free particle is
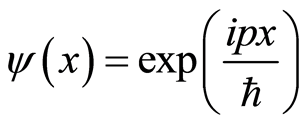 (20)
(20)
Clearly, Equation (20) is just a special form of 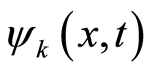 at
at 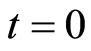 in Equation (19). Note that there is only an energy which is just the electron’s one, and the position
in Equation (19). Note that there is only an energy which is just the electron’s one, and the position 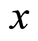 is the where the electron possibly appears. If we substitute the electron kinetic energy of
is the where the electron possibly appears. If we substitute the electron kinetic energy of 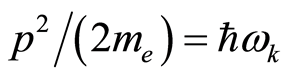 in Equation (19), we obtain
in Equation (19), we obtain
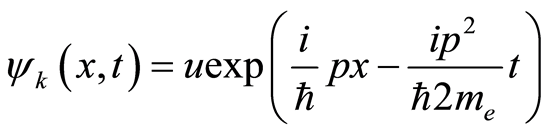 (21)
(21)
where 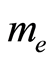 is the electron mass. This is consistent with the function given by Feynman in the path integral [24] , which is explained in terms of the probability amplitude for free electron to arrive at the point
is the electron mass. This is consistent with the function given by Feynman in the path integral [24] , which is explained in terms of the probability amplitude for free electron to arrive at the point 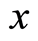 at the time
at the time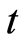 . It is certain that the wave functions of the free electron in quantum mechanics and path integral satisfy the equation of motion, which justifies that the space involving a free electron shows wave property. Since the wave motion is analogous to the simply harmonic oscillation, the subsequent wave quantization is expected. We make Fourier transformation for
. It is certain that the wave functions of the free electron in quantum mechanics and path integral satisfy the equation of motion, which justifies that the space involving a free electron shows wave property. Since the wave motion is analogous to the simply harmonic oscillation, the subsequent wave quantization is expected. We make Fourier transformation for 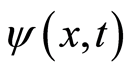
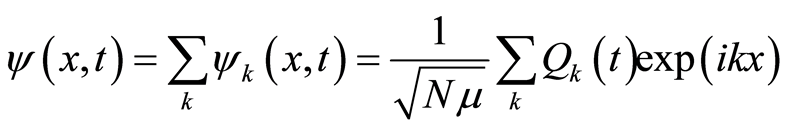 (22)
(22)
Let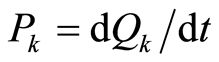 . The following treatment is familiar in quantum mechanics [27] . We introduce operators
. The following treatment is familiar in quantum mechanics [27] . We introduce operators
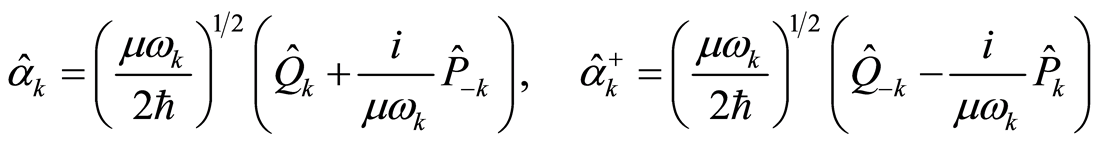 (23)
(23)
The 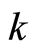 and
and 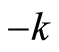 in the subscripts mean there may be both forward and backward waves simultaneously.
in the subscripts mean there may be both forward and backward waves simultaneously.
Since the square 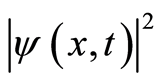 is a real number, the operators
is a real number, the operators 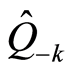 and
and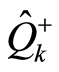 ,
, 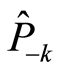 and
and 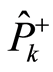 obey relations
obey relations
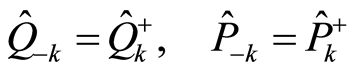 (24)
(24)
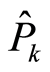 and
and 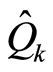 as the solutions of Equation (23) take the forms
as the solutions of Equation (23) take the forms
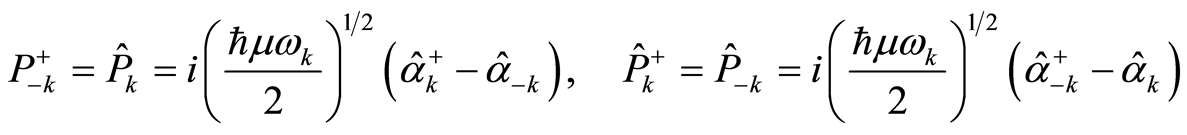 (25.1)
(25.1)
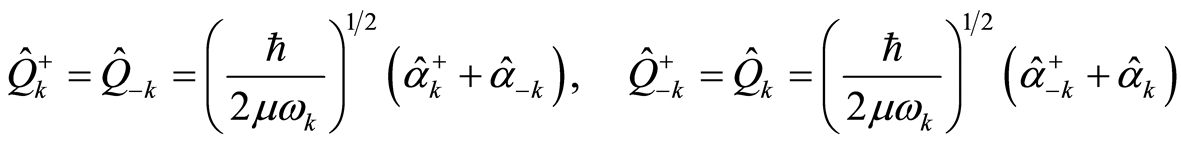 (25.2)
(25.2)
The operators 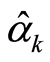 and
and 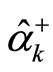 satisfy a commutation relation
satisfy a commutation relation
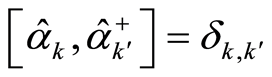 (26)
(26)
The Hamiltonian is
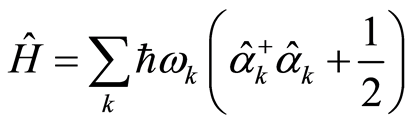 (27)
(27)
Comparing with the harmonic oscillator’s Hamiltonian in quantum mechanics, we see that the wavefunction vibration amounts to the independent harmonic oscillators with the total number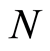 , each of which corresponds to a mode
, each of which corresponds to a mode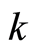 . In the particlenumber representation the oscillator eigenvalue equations are
. In the particlenumber representation the oscillator eigenvalue equations are
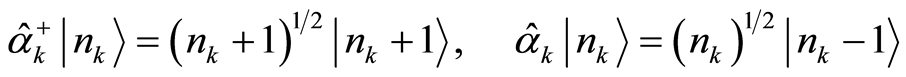 (28)
(28)
where 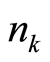 is the quantum number with mode
is the quantum number with mode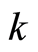 . Equation (28) states that the
. Equation (28) states that the 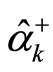 is a creation operator, the
is a creation operator, the 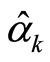 an annihilation one; and the eigenvalue equation is
an annihilation one; and the eigenvalue equation is
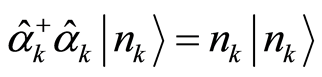 (29)
(29)
Therefore, the total energy is given by
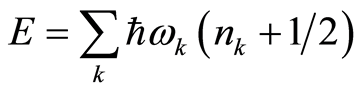 (30)
(30)
Equations (29) and (30) claim that an individual wave motion with frequency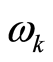 , as a whole, is equivalent to boson particles of
, as a whole, is equivalent to boson particles of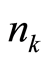 , each of which has energy
, each of which has energy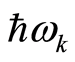 , where
, where 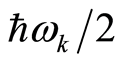 is zero-point energy. The
is zero-point energy. The 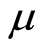 and
and 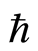 are constant. Using Equations (18), (22), (25.2), we get a correspondence relation
are constant. Using Equations (18), (22), (25.2), we get a correspondence relation
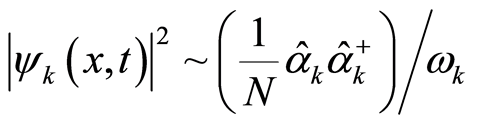 (31.1)
(31.1)
For a given state 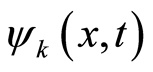 with definite position
with definite position 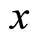 and wave vector
and wave vector 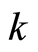 the
the 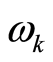 in this equation is a constant determined by Equation (16). Thus, Equation (31.1) is a link between the square of the amplitude of the wavefunction
in this equation is a constant determined by Equation (16). Thus, Equation (31.1) is a link between the square of the amplitude of the wavefunction 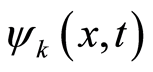 and the ratio
and the ratio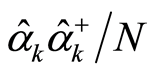 . The eigenvalue of the operator
. The eigenvalue of the operator 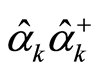 on the right side of Equation (31.1) is
on the right side of Equation (31.1) is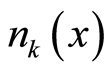 , which is the number of the boson particles with wave vector
, which is the number of the boson particles with wave vector 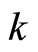 at the position
at the position 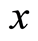 due to the locality of the square of the wavefunction amplitude. The
due to the locality of the square of the wavefunction amplitude. The 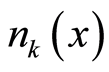 differs from the
differs from the 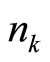 which is the total number of particles with the wave vector
which is the total number of particles with the wave vector 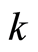 in the space; the former is local, the latter is not so. Equation
in the space; the former is local, the latter is not so. Equation
(31.1) is an one-to-one correspondence relation between 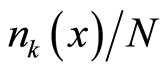 and
and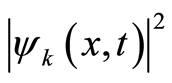 , the
, the 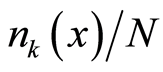 is a ratio of the number of boson particles with a wave vector
is a ratio of the number of boson particles with a wave vector 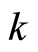 at the position
at the position 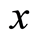 against the total number of boson particles. The meanings of the number
against the total number of boson particles. The meanings of the number 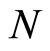 should be emphasized here. First, there are
should be emphasized here. First, there are 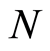 different positions in the region
different positions in the region 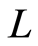 to be provided for the electron to occupy. Second, the total number of the individual modes (or wave vectors) is
to be provided for the electron to occupy. Second, the total number of the individual modes (or wave vectors) is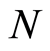 , equaling to the total number of the boson particles, since one specific mode (or wave vector) relates to one of the particles. The meaning of Equation (31.1) is explained as the following. For a uniform distribution the associated relative probability of finding the electron at each position equals to
, equaling to the total number of the boson particles, since one specific mode (or wave vector) relates to one of the particles. The meaning of Equation (31.1) is explained as the following. For a uniform distribution the associated relative probability of finding the electron at each position equals to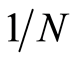 , which amounts to that one boson particle resides in one position because there are
, which amounts to that one boson particle resides in one position because there are 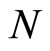 boson particles in total. In a nonuniform distribution, there are
boson particles in total. In a nonuniform distribution, there are 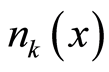 times opportunities for the electron to occupy a location
times opportunities for the electron to occupy a location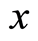 , the correspondingly relative probability of finding the electron with the wave vector
, the correspondingly relative probability of finding the electron with the wave vector 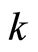 at the location
at the location 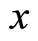 is
is 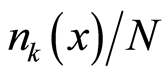 tantamount to that there are
tantamount to that there are 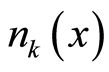 boson particles with wave vector
boson particles with wave vector 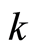 to lie in the same site
to lie in the same site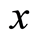 . From Equations (18), (22), (25.2), and (31.1), we have a corresponding relation further
. From Equations (18), (22), (25.2), and (31.1), we have a corresponding relation further
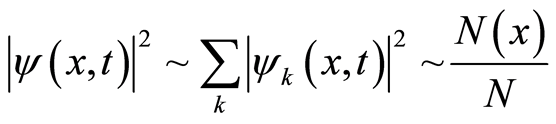 (31.2)
(31.2)
where 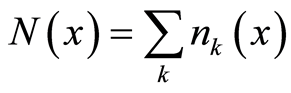 is the total number of boson particles in the position
is the total number of boson particles in the position 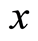 including the magnitudes of all possible wave vectors. As with Equation (31.1), the ratio
including the magnitudes of all possible wave vectors. As with Equation (31.1), the ratio 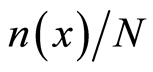 on the right side of Equation (31.2) represents the relative probability of finding the electron with all kinds of
on the right side of Equation (31.2) represents the relative probability of finding the electron with all kinds of 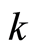 at the position
at the position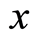 . The particle’s numbers
. The particle’s numbers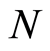 ,
,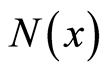 ,
, 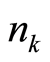 , and
, and 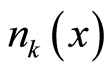 obey the following formula:
obey the following formula:
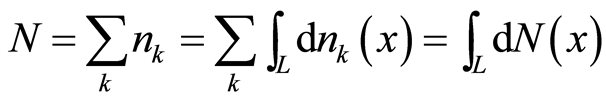 (32)
(32)
The normalization condition is
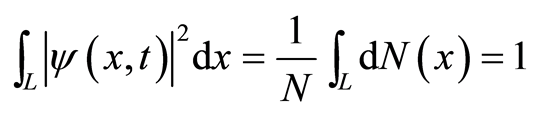 (33)
(33)
The integral is taken in the region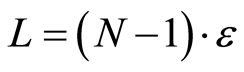 , and the number
, and the number 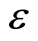 tends to infinitesimal such that the distribution of the wavefunction is continuous. Equation (31) is a theoretical evidence of the probabilistic interpretation suggested by Born. The probabilistic interpretation transfers the nonlocality of an electron to the locality of the square of the wavefunction amplitude, and the wave quantization makes the locality of the square be equivalent to the locality of the boson particles.
tends to infinitesimal such that the distribution of the wavefunction is continuous. Equation (31) is a theoretical evidence of the probabilistic interpretation suggested by Born. The probabilistic interpretation transfers the nonlocality of an electron to the locality of the square of the wavefunction amplitude, and the wave quantization makes the locality of the square be equivalent to the locality of the boson particles.
4. Different Meanings of Wave-Particle Duality for Photons and for Free Electron
Double-slit interference experiment shows that the particle’s behaves and the wave characteristics occur simultaneously [14] [20] . By equation (12), we get the wavefunction in the three dimensions:
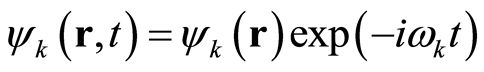
where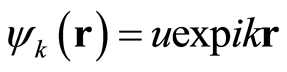 , satisfying Holmholtz equation:
, satisfying Holmholtz equation:
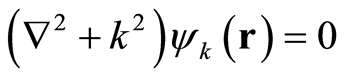 (34)
(34)
Using Equation (34) and Kirchhoff’s law, with the same reason as the radiation field [28] , we can confirm that the wave, like the light wave, will demonstrate single-slit diffraction, because of which the double-slit interference seems to proceed through the space containing free electron. A homogeneous wave equation is set up using the wavefunction:
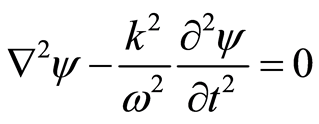 (35)
(35)
If we put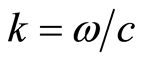 , where
, where 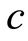 is the light velocity, this equation becomes
is the light velocity, this equation becomes
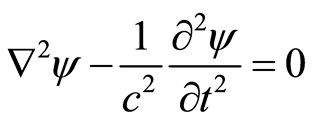 (36)
(36)
This is just the light’s wave equation in classical theory [28] . Equations (12), (34), (35), and (36) tell us that the radiation field and the space containing a free electron show some similar wave properties. Note that the wavefunctions are obtained by the classical dynamical equation, and the Equation (34) and (35) are also classical, which explicitly shows that the wave that refers to the space involving a free electron does be a classical phenomenon. For light, its wavefunction is the vector potential of the electromagnetic field, which can bring us vision effect, different from the wavefunction of the space containing a free electron. Therefore, a photon is not equivalent to a particle coming from the wave quantization of the space involving the electron, although both are bosons. In addition, double-slit interference experiment shows that these boson particles associated with the electron do not interact with the detector, except the electron. For light, the wave-particle duality refers to the same object: the light exhibits wave characteristics and the wave quantization leads to photons. For the free electron, however, the wave belong to the space containing the electron, but the electron alone, and the wave quantization leads to the boson particles distinguishable from the electron, the former are immaterial and the latter is material. The same probabilistic interpretation has different meanings for the light and for the electron. In the discussion of the probability of finding photons at a position, the wave quantization theory tells us that the number of photons at the position is usually greater than one photon, since there are 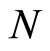 photon s in the space where the light propagates, and the number
photon s in the space where the light propagates, and the number 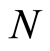 tends to infinity. When the probabilistic interpretation describes the probability of finding a free electron at a position, the number of particles at the position is not the electron’s number but the number of boson particles, which only represent the potential opportunities of the electron to occupy the position, since there is a single electron. That the huge number of the boson particles can be described by statistical theory is the reason why the probabilistic interpretation is applicable to a single electron.
tends to infinity. When the probabilistic interpretation describes the probability of finding a free electron at a position, the number of particles at the position is not the electron’s number but the number of boson particles, which only represent the potential opportunities of the electron to occupy the position, since there is a single electron. That the huge number of the boson particles can be described by statistical theory is the reason why the probabilistic interpretation is applicable to a single electron.
5. Concluding Remark
Uncertainty relations are the intrinsic attributes of the real spaces. The bosons turning out from the wave quantizations are local in the position space because of the locality of the square of the wavefunction amplitude. These particles are immaterial and called as pseudo particles, which means that the pseudo particles may be of locality. In this sense, the Einstein’s memorable remark “God does not play dice” is correct. In contrast, electron as a material particle is of nonlocality.