Some Lacunary Sequence Spaces of Invariant Means Defined by Musielak-Orlicz Functions on 2-Norm Space ()
1. Introduction
Let 
be the set of all sequences of real numbers 
and 
be respectively the Banach spaces of bounded, convergent and null sequences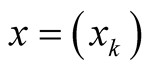 
with 
or 
the usual norm
, where
, the positive integers.
The idea of difference sequence spaces was first introduced by Kizmaz [1] and then the concept was generalized by Et and Çolak [2] . Later on Et and Esi [3] extended the difference sequence spaces to the sequence spaces:
for 
and
, where 
be any fixed sequence of non zero complex numbers and
The generalized difference operator has the following binomial representation,
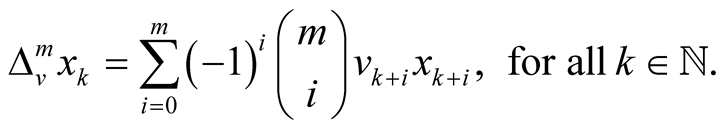
The sequence spaces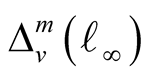
, 
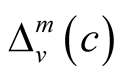and 
are Banach spaces normed by
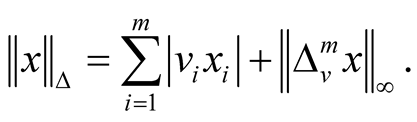
The concept of 2-normed space was initially introduces by Gahler [4] as an interesting linear generalization of normed linear space which was subsequently studied by many others [5] [6] ). Recently a lot of activities have started to study summability, sequence spaces and related topics in these linear spaces [7] [8] ).
Let 
be a real vector space of dimension
, where
. A 2-norme on 
is a function 
which satisfies:
1) 
if and only if 
and 
are linearly dependent2)
3)
4)
.
The pair 
is called a 2-normed space. As an example of a 2-normed space we may take 
being equiped with the 2-norm 
= the area os paralelogram spaned by the vectors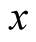 
and
, which may be given explicitly by the formula
.
Then clearly 
is 2-normed space. Recall that 
is a 2-Banach space if every cauchy sequence in 
is convergent to some
.
Let 
be a mapping of the positive integers into itself. A continuous linear functional 
on 
is said to be an invariant mean or 
-mean if and only if 1)
, when the sequence 
has, 
for all
2)
3) 
for all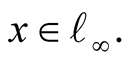 
If
, where
. It can be shown that
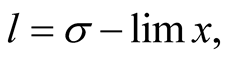where
[9] .
In the case 
is the translation mapping
, 
-mean is often called a Banach limit and 
the set of bounded sequences of all whose invariant means are equal is the set of almost convergent sequence [10] .
By Lacunary sequenc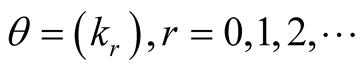e 
where 
we mean an increasing sequence of non negative integers
. The intervals determined by 
are denoted by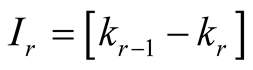 
and the ratio 
will be denoted by
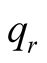. The space of lacunary strongly convergent sequence 
was defined by Freedman et al. [11] as follows:
An Orlicz function is a function 
which is continuous, non-decreasing and convex with 
for 
and 
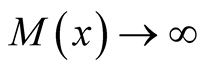as 
It is well known that if 
is convex function and 
then
, for all 
with 
Lindenstrauss and Tzafriri [12] used the idea of Orlicz function and defined the sequence space which was called an Orlicz sequence space 
such as
which was a Banach space with the norm
which was called an Orlicz sequence space. The 
was closely related to the space 
which was an Orlicz sequence space with 
for
. Later the Orlicz sequence spaces were investigated by Prashar and Choudhry [13] , Maddox [14] , Tripathy et al. [15] -[17] and many others.
A sequence of function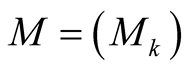 
of Orlicz function is called a Musielak-Orlicz function [18] [19] . Also a Musielak-Orlicz function 
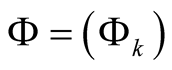is called complementary function of a Musielak-Orlicz function 
if
For a given Musielak-Orlicz function
, the Musielak-Orlicz sequence space 
and its subspaces 
are defined as follow:
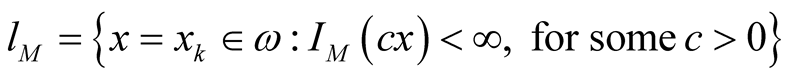
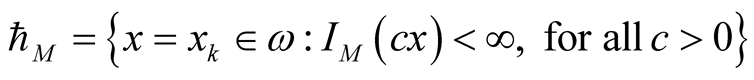
where 
is a convex modular defined by
We consider 
equipped with the Luxemburg norm
or equipped with the Orlicz norm
The main purpose of this paper is to introduce the following sequence spaces and examine some properties of the resulting sequence spaces. Let 
be a Musielak-Orlicz function, 
is called a 2-normed space. Let 
be any sequences of positive real numbers, for all 
and 
such that
. Let 
be any real number such that
. By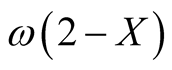 
we denote the space of all sequences defined over
. Then we define the following sequence spaces:
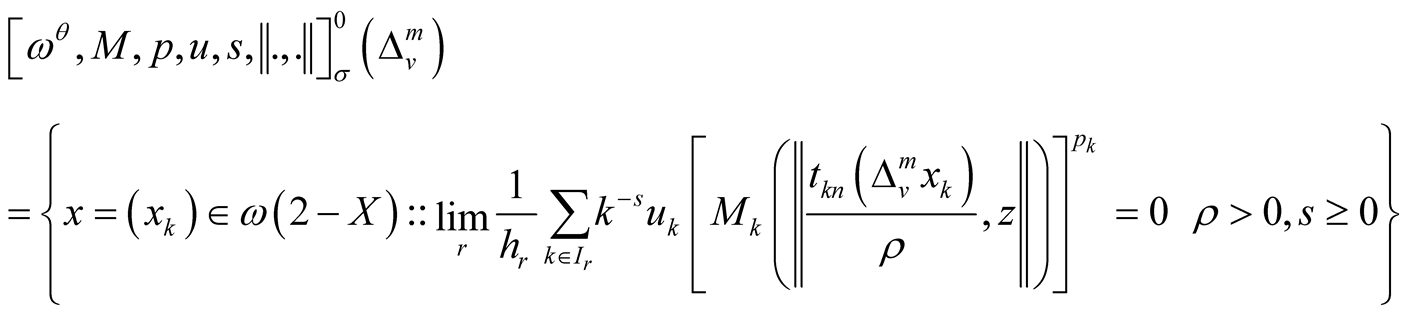
Definition 1. A sequence space 
is said to be solid or normal if 
whenever 
and for all sequences of scalar 
with 
[20] .
Definition 2. A sequence space 
is said to be monotone if it contains the canonical pre-images of all its steps spaces, [20] .
Definition 3. If 
is a Banach space normed by
, then 
is also Banach space normed by
Remark 1. The following inequality will be used throughout the paper. Let 
be a positive sequence of real numbers with
,
. Then for all 
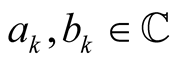for all
. We have
(1)
2. Main Results
Theorem 1. Let 
be a Musielak-Orlicz function, 
be a bounded sequence of positive real number and 
be a lacunary sequence. Then 
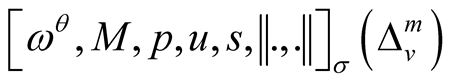
and 
are linear spaces over the field of complex numbers.
Proof 1. Let 
and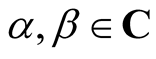
. In order to prove the result we need to find some 
such that,
Since
, there exist positive 
such that
and
Define 
Since 
is non decreasing and convex
So that 
This completes the proof. Similarly, we can prove that 
and 
are linear spaces.
Theorem 2. Let 
be a Musielak-Orlicz function, 
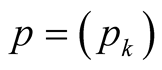be a bounded sequence of positive real number and 
be a lacunary sequence. Then 
is a topological linear space totalparanormed by
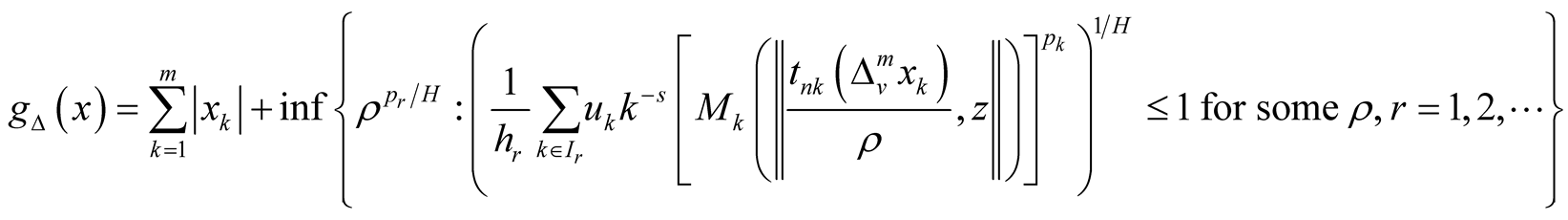
Proof 2. Clearly
. Since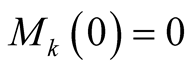
, for all
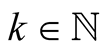. we get
, for 
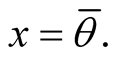Let
, 
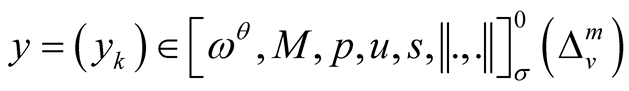and let us choose 
and 
such that
and
Let
, then we have
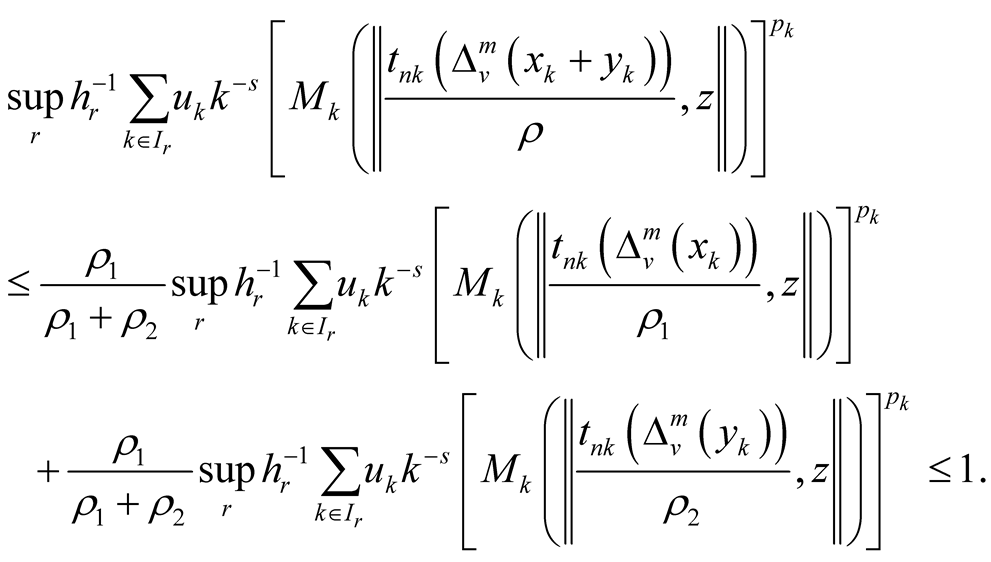
Since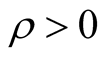
, we have
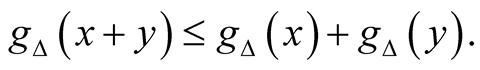
Finally, we prove that the scalar multiplication is continuous. Let 
be a given non zero scalar in
. Then the continuity of the product follows from the following expression.
wher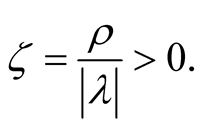e 
Since
,
This completes the proof of this theorem.
Theorem 3. Let 
be a Musielak-Orlicz function, 
be a bounded sequence of positive real number and 
be a lacunary sequence. Then
Proof 3. The inclusion 
is obvious. Let
. Then there exists some positive number 
such that
as
, uniformly in
. Define
. Since 
is non decreasing and convex for all
, we have
where
, 
by (1).
Thus
.
Theorem 4. Let 
be a Musielak-Orlicz functions. If 
for all
, then
Proof 4. Let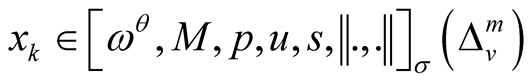 
by using (1), we have
Since
, we can take the
. Hence we can get
.
This complete the proof.
Theorem 5. Let 
be fixed integer. Then the following statements are equivalent:
1)
2)
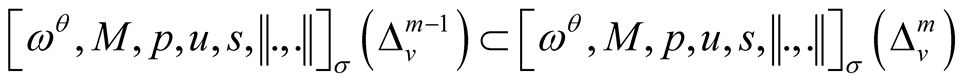3) 
Proof 5. Let 
Then there exist 
such that
Since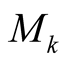 
is non decreasing and convex, we have
Taking
, we have
i.e. 
The rest of these cases can be proved in similar way.
Theorem 6. Let 
and 
be two Musielak-Orlicz functions. Then we have 1) 
2) 
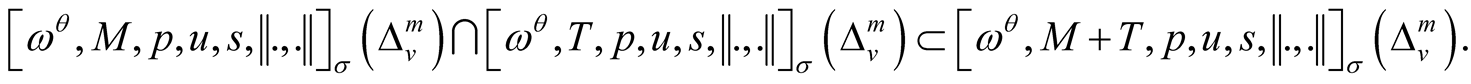
3) 
Proof 6. Let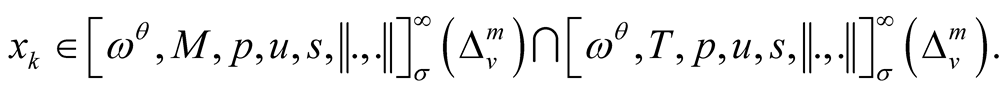 
Then
and
uniformly in n. We have
by (1). Applying 
and multiplying by 
and 
both side of this inequality, we get
uniformly in n. This completes the proof 2) and 3) can be proved similar to 1).
Theorem 7. 1) The sequence spaces 
and 
are solid and hence they are monotone.
2) The space 
is not monotone and neither solid nor perfect.
Proof 7. We give the proof for
. Let 
and 
be a sequence of scalars such that 
for all
. Then we have
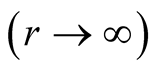, uniformly in n. Hence 
for all sequence of scalars 
with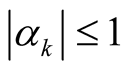 
for all
, whenever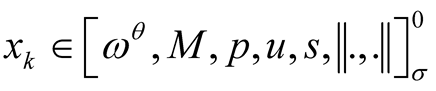
. The spaces are monotone follows from the remark (1).