1. Introduction
The flow between porous discs has been studied by several authors. As in the case of porous pipes and porous channels, the governing equation reduces to a set of nonlinear ordinary differential equations. This problem was first studied by Batchelor [1] who generalized the solution of Von Karman [2] . Further this problem was analyzed by Stewartson [3] who obtained perturbation solution for the small Reynolds number. Flow between a rotating and a stationary disc has been studied by Phan-Thein and Bush [4] . The problem of suction of viscous in incompressible fluid through a rotating porous disc onto a rotating co-axial disc was studied by C. Y. Wang [5] . Here we view this problem as a coupled nonlinear boundary value problem.
In the present paper we have used semianalytical numerical technique to understand the effect of suction represented by a pair of nonlinear differential equations. For simple geometrics the semianalytical numerical methods proposed here provide better results. Van Dyke [6] and his associates have successfully used these series methods in unveiling important features of various types of fluid flows. Bujurke and Pai [7] has discussed similar geometrical problem with injection at the discs.
Recently in the analysis of flow in pipe, Pai and Katagi [8] have used series analysis satisfactorily. The physical problem considered in this paper is of great importance in Fluid Dynamics. The present study is a possible extension work of Wang [5] . The problem is solved using a special type of series. The series so generated has limited utility due to presence of a singularity and its region of validity is extended by analytic continuation.
2. Mathematical Formulation
As shown in the Figure 1 we denote the spacing between the discs by 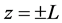 and rotating with the same angular velocity Ω. Fluid is withdrawn from both discs with velocity W. We shall assume the gap with 2L is small compared to diameter of the discs. So that end effects can be neglected. The flow field is symmetric about the
and rotating with the same angular velocity Ω. Fluid is withdrawn from both discs with velocity W. We shall assume the gap with 2L is small compared to diameter of the discs. So that end effects can be neglected. The flow field is symmetric about the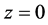 .
.
The governing equations are
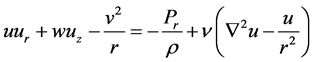 (1.1)
(1.1)
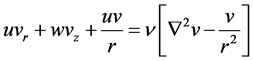 (1.2)
(1.2)
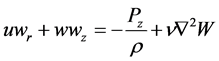 (1.3)
(1.3)
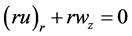 (1.4)
(1.4)
where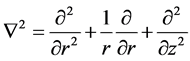 , and u, v, w are velocity components. The boundary conditions are at
, and u, v, w are velocity components. The boundary conditions are at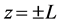 ,
, 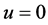 ,
, 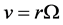 ,
,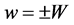 .
.
For similarity transformation we consider Wang [5]
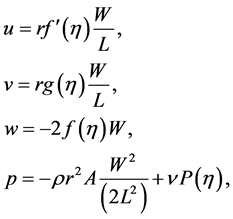 (1.5)
(1.5)
where 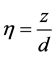 and A is constant. Now the equations take the form
and A is constant. Now the equations take the form
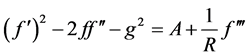
or
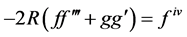 (1.6)
(1.6)
![]() (1.7)
(1.7)
![]() (1.8)
(1.8)
Here ![]() is Reynolds number. The boundary conditions are
is Reynolds number. The boundary conditions are
![]() (1.9)
(1.9)
![]() (1.10)
(1.10)
3. Method of Solution
We assume the solution of (1.6) and (1.7) in the forms
![]() (3.1)
(3.1)
![]() (3.2)
(3.2)
Substituting (3.1), (3.2) in (1.6) and (1.7) and comparing powers of R one can get
![]() (3.3)
(3.3)
![]() (3.4)
(3.4)
The relevant boundary conditions are
![]()
![]()
![]()
![]()
The solutions are
![]()
![]()
![]()
![]()
![]()
The slow convergence of series (3.1), (3.2) requires large number of terms for obtaining the approximate sum. For higher order approximations we proceed by the following scheme.
We propose a systematic scheme for this purpose, we consider ![]() and
and ![]() to be of the forms
to be of the forms
![]() (3.5)
(3.5)
![]() (3.6)
(3.6)
We substitute (3.5), (3.6) in (3.3), (3.4) respectively and equate various powers of ![]() on both sides to get
on both sides to get
![]() (3.7)
(3.7)
![]() (3.8)
(3.8)
where![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ’s are functions of k and
’s are functions of k and![]() .
.
For the radial velocity profile,
![]() (3.9)
(3.9)
And we have
![]() (3.10)
(3.10)
4. Conclusions
A new type of series is presented for studying the problems of flow between the two discs using recurrences (3.7) and (3.8). In this process we generate universal coefficients![]() ,
, ![]() ,
,![]() .
.
These coefficients in turn give universal coefficients for![]() . The series (3.9) and (3.10) give
. The series (3.9) and (3.10) give ![]() and
and ![]() respectively using Domb-sykes plot (Figure 2), and we locate the position of singularities for
respectively using Domb-sykes plot (Figure 2), and we locate the position of singularities for ![]() at 17.89. The series (3.9) and (3.10) are summed using Pade-approximants. Earlier numerical results were from
at 17.89. The series (3.9) and (3.10) are summed using Pade-approximants. Earlier numerical results were from ![]() to −39. We are able to go upto
to −39. We are able to go upto ![]() to −60 using Pade-approximants. The results are in close agreement with numerical findings of Wang [5] which are shown in the Table 1 and Table 2.
to −60 using Pade-approximants. The results are in close agreement with numerical findings of Wang [5] which are shown in the Table 1 and Table 2.