A Quantistic Interpretation of the Relationship between the Earth-Core and the Atmosphere ()
1. Introduction
Weather patterns are intriguing aspects of the planets’ atmospheric system and have been studied with modern technologies for decades, showing several crucial relationships governing the weather patterns, such as solar cycles and low-/high-pressure systems [1] . Additionally, solar storms and solar spot prevalence affect directly the dynamics of the earth’s atmosphere [2] [3] . Other earth-like planets, such as Mars, are also subjected to similar patterns, and most intriguingly, Martian atmospheric systems have been found to be affected by gravity, as the variation of Martian gravity affects the physical conditions of its atmospheric gases [4] . Establishing an analogy between Martian and earth atmospheric behaviour and their relation with gravity is in this context critical. The analogy between Mars and Earth has also earlier been used to compare the effects on the atmosphere from the gravitational field: on Mars, most of the atmosphere has throughout planetary evolution disappeared given a weakening in its gravitational electromagnetic field. The electromagnetic field existing on Mars [5] [6] , Earth and other planets is a direct result of the internal molten core rotation about its centre, which generates the electromagnetic field as result of the flux of electromagnetic forces resulting from its “dynamo” effects arising between the interaction of the North and South Poles [7] . This theory, originating from Malkus, published in the journal Science in 1968, has later been proven and studied in detail in Nature Geoscience in 2008 [8] . The interactions between the molten core, the electromagnetic field and the atmospheric conditions have however not been directly conceived.
In recent studies on the nature of the earth’s molten core, de Wijis and colleagues show that it has several properties alike to viscous liquids [9] . Also, the interesting finding by Wijis et al. is that the effects of the molten core affect also its magnetic properties, resulting in effects on the earths electromagnetic field [9] . Nevertheless, the understanding of the earth’s molten core dynamics has not reached its peak until recent studies show that the very forces that govern the earth’s molten core, gravitational fields, are governed by the same laws used in quantum mechanics. In the study published by Nesvizhevsky et al. in Nature in 2002 [10] , the use of neutrons has aided in demonstrating that the earths gravitational field can be quantized in a similar fashion as neutrons. Neutrons are fermions, which are subjected to the same laws of quantum physics as electrons and protons, and have their potential energy quantized according to quantum theory [11] [12] . In this rationale for conceiving the relationship between energy and matter, all elementary particles are described hence to a wave and a particle component. Particles are affected by their surroundings, such as by gravitational fields, which are considered extremely weak [10] , however, gravitational fields have also been assigned a quantizable wave component, such as for matters, as in the model by Nesvizhevsky and colleagues [10] , which has earned great acclaim in the field of physics. The effects on matter from gravitational fields, such as the Earths gravitational field are thus expected to follow the same principles of quantization.
In this context, the work by Nesvizhevsky and colleagues [10] assists in relating a crucial part of quantum physics to atmospheric behaviour. Here, the use of quantum numbers assists in understanding that the Earths gravity can have quantizable effects on its particle surroundings, with a particular emphasis on the atmosphere.
Any quantized state has its sub-states, known as the second, third and forth quantum numbers [13] , which are usually attributed to fermions, such as electrons. These quantum numbers are useful when considering the gravitational force field quantistic properties [10] , which include one crucial component for the possible better understanding of atmospheric dynamics: the third quantum number; a projection of the gravitational force field with a term-value and magnitude.
In order to better explain this theory, a simple demonstration of the third quantum number is sketched in Figure 1. Following Figure 1, one can observe that the number of projections of an impulse (e.g. momentum, gravity) is quantized and directly dependent on the intensity of the impulse. In order to further understand how the projections of the gravity (described by quantum number 3) can be related to atmospheric elements such as high and low-pressure systems, the following paragraph delineates this in depth.
2. Quantistic Relationship between Gravity and Atmospheric Dynamics
In Figure 2 the projection of the angular momentum, the third quantum number is illustrated descriptively as a vortex force. The vortex length displays its intensity and the vortex direction displays its projection. Inherited to the quantistic properties of the gravitational force field [10] , and accounting for that the gravitational force field has effects on atmospheric components [4] , the model depicted in Figure 1 displays how the earths gravitational field may affect the atmosphere quantistically, in a fashion related to the four quantum numbers (Figure 2).
The first quantum number, the energy level. This number is related to the energy state of the particle in quantum mechanical terms. The energy describes the potential energy of the particle hence to a reference (normally an infinite distance between the particle and the nucleus). The second quantum number, the angular momentum. The angular momentum delineates the momentum induced on the particle by its dynamical behaviour about a core (nucleus). The third quantum number represents the projection of the angular momentum (magnetic quantum

Figure 1. The projections of the angular momentum (m), illustrated with the angular momentum (l) [13] . Values of m are designated for 5 different projections of the angular momentum.

Figure 2. Proposed nature of projections of the quantized gravitational field. The proven quantized gravitational field [10] is here illustrated in context with the properties of the third quantum number (m), which depicts the direction of the angular momentum (l). The long cone towards a High-Pressure system (H) depicts a narrow but intense effect of quantized gravitational effect of a specific projection number. The wide cone illustrates a weaker but wide-impact projection of the gravitational force field intensity, projected towards a Low-pressure System (L). The gravitational intensity effect has an effect on the weight of the air in the atmosphere, giving rise to High (H) and Low (L) pressure effects in the atmospheric subdivision.
number). The projection, as named above, describes the orientation of the angular momentum from the core. The fourth quantum number is the spin. The spin discerns between oppositely spinning particles, attributed inverse signs.
3. Properties of Atmospheric Dynamics and Quantized Gravitational Forces
The dynamics of highand low-pressure systems are in meteorological sciences assigned to pressure, temperature and humidity. The former, a direct result of the weight of the earth’s atmosphere on the surface, represents here a central property to the demonstrated quantistic properties of the earth’s gravity [10] . As the earths gravity is variational and not uniform [14] , and the gravitational field has quantistic properties [10] , interpreting the formation of high and low pressure systems from a quantistic gravitational perspective introduces a new model for the interpretation of atmospheric dynamics. In quantum theory, the projection of the angular momentum is used to describe the states of the angular momentum (e.g. +1, −1, +2, −2), which are illustrated as levels of projections in space. In a similar fashion, High and Low pressure systems occur in a band-like formations across the planet (see below), and find direct compatibility with the third quantum number, oriented in a (+) projection (Northern hemisphere) and (–) projection (Southern hemisphere). Their different inherent intensities are attributed to the non-uniform properties of gravity [14] , and its effects in inducing high or low pressure by high or low gravitational impulses.
4. Occurrence of High and Low Pressure Centres at Projection Centers of the Third Quantum Number of Gravitational Field
The theoretical model depicted herein, encompasses a model where the third quantum number, is a central property in governing the occurrence of Low and High pressure systems. Upon high pressure, the gravitational field has the projection intensified in the direction of the centre of the High pressure system (Figure 2). During Low pressure system, the projection of the gravitational fields is reduced in the direction of the Low-pressure system, and the gravitational intensity on the local air masses yields a lower pressure, by the reduced gravitational pull. Figure 2 illustrates this simple rationale. This pattern can also be viewed in the general occurrence of localized bands of high and low pressure systems across the northern and southern hemisphere, as recently seen in a series of images captured during the year 2013 by the European Organisation for the Exploitation of Meteorological Satellites [15] . As seen in the satellite data at the EUMETSTAT Institute, the bands occur at specific bands between the tropics and the higher latitudes of the globe, on the Southern (−) and the Northern (+) projections. The nature of the high and low pressure system can also itself be well explained by quantum mechanical operators, as reported recently in a parallel study [16] , and the relationship between the behaviour of atmospheric components and the gravity can therefore find a putative formulation in the relationships as reported in herein and in context with the expression provided recently [16] .
5. Mathematical Expressions
Deriving mathematical expression to explain and support this theory in not trivial. As the gravity field of earth has quantizable characteristics [10] , a description to satisfy its exertion on the atmospheric masses, must root in a model for either a particle or a wave-function property of the field. As the former is relying on the existence of a particle with a momentum, the lack of momentum of the gravitational field makes it untrivial to derive a quantizable wave function for it. The latter, which relies on the frequency of oscillation of an electromagnetic boson, describes instead that the field must have an amplitude, which is not the case, unless one considers the fields strength which declines exponentially from the center of gravity. In this case, the earth core is the center of gravity, and the gravitational effects decline with distance from the earth’s surface, and as cumulus clouds are the only types of systems which have a considerable height, their properties can highlight the effects exerted from the gravitational field, where the dense regions of air in the cumulus clouds localize at the bottom. Nevertheless, this does not give a sufficient mathematical basis to describe the formation of high and low pressure systems in respect with the earth core quantized gravitational field, and for that reason need to rely on a different start point. The start point of interest is in applying Poynting vectors, which describe the intensity of electric and magnetic fields, which use the Abraham form:
 where S is the cross-product of the electric field and the magnetic field. If one quantizes S, in a similar approach to quantizing the kinetic energy of a particle, T, in quantum physics, a set of equations can be derived for quantizing a gravity field into high and low pressure areas at a global scale. First, this is due to that the conventional gravity expressions described by relativity theory are not appropriate for such small scale effects, such as earth gravity’s effect on the atmospheric masses. Second, using solely magnetic and electric field-related expressions, which are appropriate for mesoscopic phenomena of electricity and magnetic fields interacting with matter, would not be correct for the large scale effects occurring at the level of gravity affecting air masses.
where S is the cross-product of the electric field and the magnetic field. If one quantizes S, in a similar approach to quantizing the kinetic energy of a particle, T, in quantum physics, a set of equations can be derived for quantizing a gravity field into high and low pressure areas at a global scale. First, this is due to that the conventional gravity expressions described by relativity theory are not appropriate for such small scale effects, such as earth gravity’s effect on the atmospheric masses. Second, using solely magnetic and electric field-related expressions, which are appropriate for mesoscopic phenomena of electricity and magnetic fields interacting with matter, would not be correct for the large scale effects occurring at the level of gravity affecting air masses.
Quantizing a large scale factor equivalent to S would be the closest approximation to a suitable model to rationalize the effects of the gravity field on the air masses, where, Σ (a macroscopic equivalent to the Poynting vector S) describes the physical force which derives from the gravity which is quantizable, acting on the atmospheric masses. Quantizing Σ would obey the same laws for quantum mechanics. Here we call S, Σ, and give that Σ is a function describing the macroscopic pointing vector of the gravitational projection in a specific direction. Υ is the potential energy of the air mass. The sum of these two forces, the function describing the macroscopic Poynting vector towards the respective high-pressure system and the potential energy of the air masses, is give by Γ.
So in respect to a quantistic rationale, the total quantized force acting on the air-masses is:
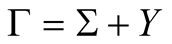 . (1)
. (1)
The differential equation Σ must respect the existence of a “particle-like” entity to describe the effect on the air masses in a similar fashion to quantum mechanics. This gives the use of considering the center of the high-pressure (for instance) system as the “particle” of relevance. This “particle” has a momentum, given by p, and it has a kinetic energy, when moving across the earth surface:
 .
.
Its potential energy is simply:
 similar to the spring oscillatory behaviour.
similar to the spring oscillatory behaviour.
So adapting the form in (1) to quantum mechanics gives:
 , (2)
, (2)
where Ψ is the wavefunction that obeys the observable quantization for the gravity field [10] .
Finding a quantizable function for Ψ relies on measuring the effect of the Poynting vector on air masses with potential energy Y, confined in an atmospheric radius defined by a pressure-threshold (adapting conventional air pressure limits to high and low pressure system classification). The movement of the high pressure system and its center of intensity (which describes the Poynting vector coordinates) are then used to derive Σ. The total energy of the system is the quantized by finding the suitable expressions satisfying Ψ. When Ψ satisfies the Equation (2), it proves that the earths high and low pressure systems follow quantizable patterns of behaviour, and supports furthermore the findings by [10] .
6. Conclusion
Matter and energy are considered as unified, however crucial differences between the two give rise to the requirement of quantum mechanical operators to describe elementary particle behaviour. Modelling ultra-weak forces such as gravity and their interaction with matter is an even more difficult task to carry out. Nevertheless, the recent findings which quantize the nature of gravity have assisted here in understanding its behaviour in relationship to atmospheric effects, such as dynamics of highand low-pressure systems. As these systems are not completely linear in patterns of occurrence, the foundations of quantum mechanics have been used here to interpret the behaviour of changing air pressure patterns, by adopting the nature of the third quantum number, the magnetic quantum number, which in elementary physics describes the projection of a force exerted on a particle. In this theory, the particle is the air-masses and the centre is the quantistically resolved gravitational force field [10] . The theory does not disagree with present conception of gravity [14] and rather co-joins the prerequisites of quantum theory [11] [12] attributed to gravity [10] to understand the origin of High and Low pressure systems. Solving the Equation (2) is nevertheless required to prove this theory.