Embeddings of Almost Hermitian Manifold in Almost Hyper Hermitian Manifold and Complex (Hypercomplex) Numbers in Riemannian Geometry ()
1. Deformations of Tensor Structures on a Normal Tubular Neighborhood of a Submanifold
1˚. Let 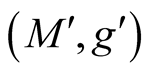 be a k-dimensional Riemannian manifold isometrically embedded in a n-dimensional Riemannian manifold
be a k-dimensional Riemannian manifold isometrically embedded in a n-dimensional Riemannian manifold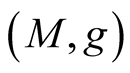 . The restriction of g to
. The restriction of g to 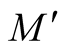 coincides with g′ and for any
coincides with g′ and for any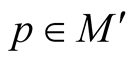 .
.
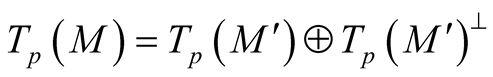 .
.
So, we obtain a vector bundle 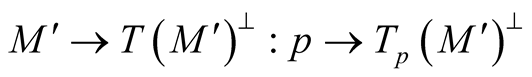 over the submanifold
over the submanifold . There exists a neighborhood
. There exists a neighborhood  of the null section
of the null section  in
in 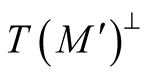 such that the mapping
such that the mapping
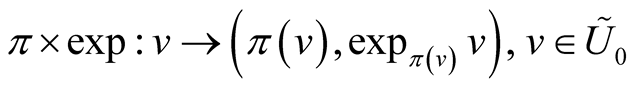 is a diffeomorphism of
is a diffeomorphism of 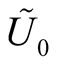 onto an open subset
onto an open subset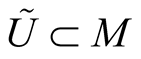 . The subset
. The subset 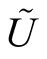 is called a tubular neighborhood of the submanifold
is called a tubular neighborhood of the submanifold 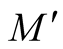 in
in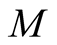 .
.
For any point  we can consider a set
we can consider a set 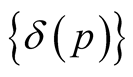 of positive numbers such that the mapping
of positive numbers such that the mapping 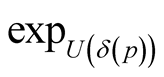 is defined and injective on
is defined and injective on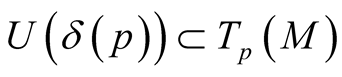 . Let
. Let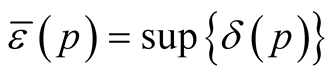 .
.
Lemma [1] . The mapping 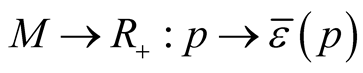 is continuous on M.
is continuous on M.
If we take the restriction of the function 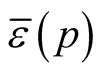 on
on 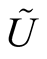 then it is clear that there exists a continuous positive function
then it is clear that there exists a continuous positive function 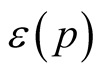 on
on 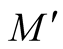 such that for any
such that for any 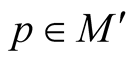 open geodesic balls
open geodesic balls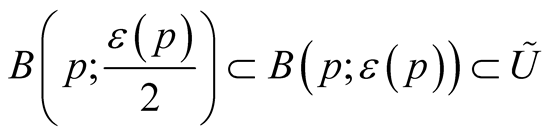 . For compact manifolds we can choose a constant function
. For compact manifolds we can choose a constant function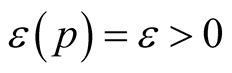 . We denote
. We denote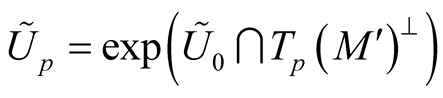 ,
, 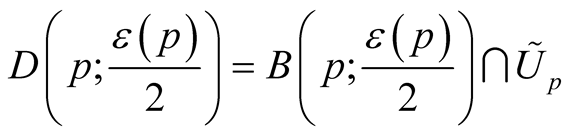 ,
,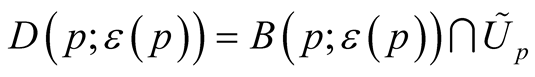 . It is obvious that
. It is obvious that
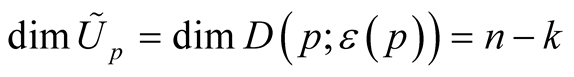 . For any point
. For any point 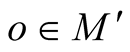 we can consider such an orthonormal frame
we can consider such an orthonormal frame
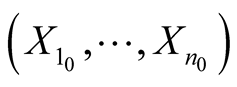 that
that 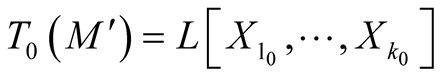 and
and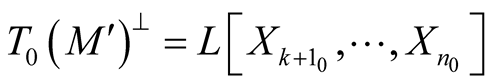 . There exist coordinates
. There exist coordinates
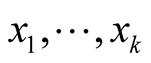 in some neighborhood
in some neighborhood 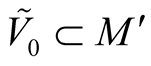 of the point o that
of the point o that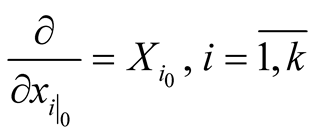 . We consider orthonormal vector fields
. We consider orthonormal vector fields 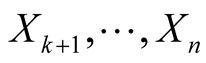 which are cross-sections of the vector bundle
which are cross-sections of the vector bundle 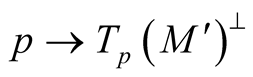 over
over  and the neighborhood
and the neighborhood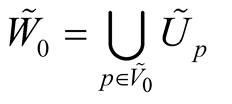 . The basis
. The basis 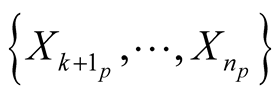 defines the normal coordinates
defines the normal coordinates 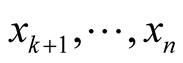 on
on 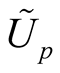
[2] . For any point 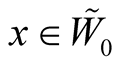 there exists such unique point
there exists such unique point 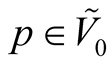 that
that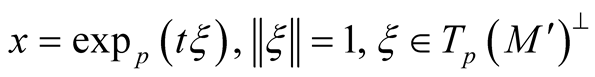 . A point
. A point 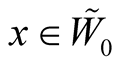 has the coordinates
has the coordinates 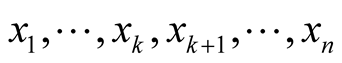 where
where  are coordinates of the point p in
are coordinates of the point p in 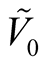
and 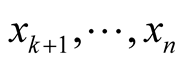 are normal coordinates of x in
are normal coordinates of x in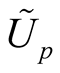 . We denote
. We denote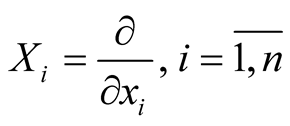 , on
, on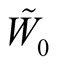 . Thus, we can consider tubular neighborhoods
. Thus, we can consider tubular neighborhoods 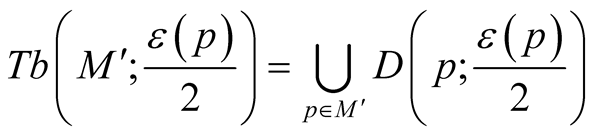 and
and 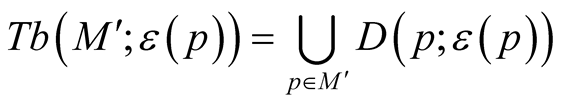 of the submanifold
of the submanifold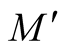 .
.
2˚. Let K be a smooth tensor field of type (r, s) on the manifold M and for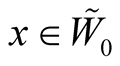 , let
, let
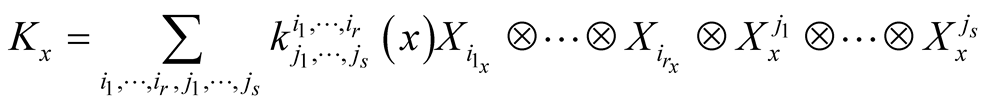 where
where 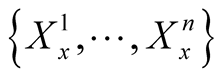 is the dual basis of
is the dual basis of 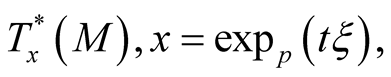
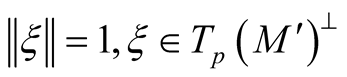 . We define a tensor field
. We define a tensor field 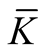 on M in the following way.
on M in the following way.
a)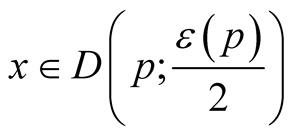 , then
, then
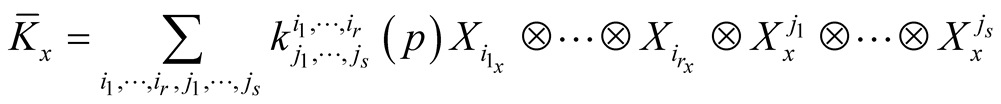 ;
;
b)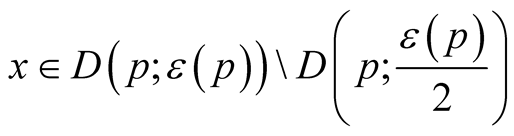 , then
, then
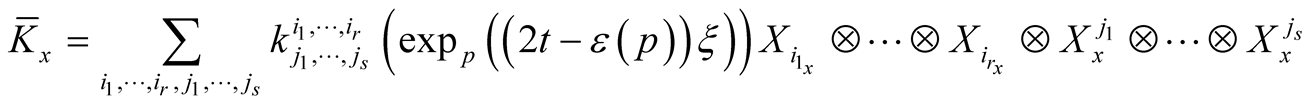 ;
;
c)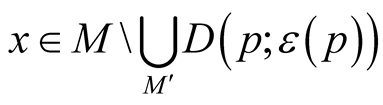 , then
, then
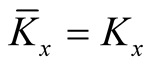 .
.
It is easy to see the independence of the tensor field 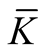 on a choice of coordinates in
on a choice of coordinates in 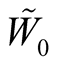 for every point
for every point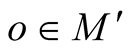 .
.
Definition 1. The tensor field 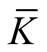 is called a deformation of the tensor field K on the normal tubular neighborhood of a submanifold
is called a deformation of the tensor field K on the normal tubular neighborhood of a submanifold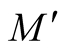 .
.
Remark. The obtained tensor field 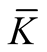 is continuous but is not smooth on the boundaries of the normal tubular neighborhoods
is continuous but is not smooth on the boundaries of the normal tubular neighborhoods 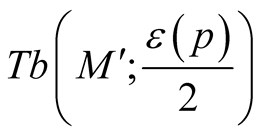 and
and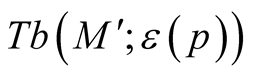 ;
;  is smooth in other points of the manifold M.
is smooth in other points of the manifold M.
3˚. We consider a deformation 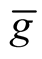 of the Riemannian metric g on the normal tubular neighborhood
of the Riemannian metric g on the normal tubular neighborhood
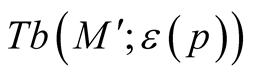 of a submanifold
of a submanifold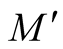 . For
. For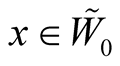 ,
, 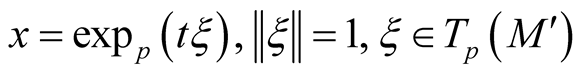 , we define the Riemannian metric
, we define the Riemannian metric 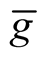 by the following way.
by the following way.
a) 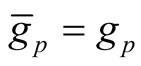 for any
for any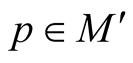 ;
;
b)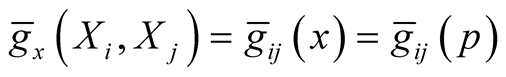 , where
, where 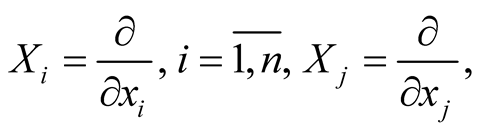
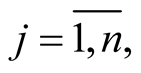 on
on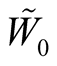 ,
,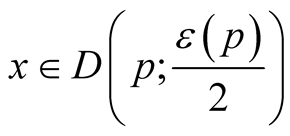 ;
;
c)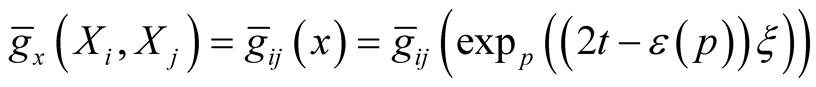 , for any
, for any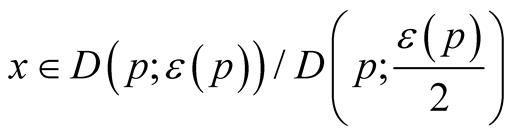 ;
;
d) 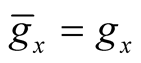 for each point
for each point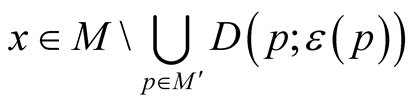 .
.
The independence of 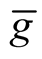 on a choice of local coordinates follows and the correctly defined Riemannian metric
on a choice of local coordinates follows and the correctly defined Riemannian metric 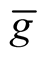 on M has been obtained.
on M has been obtained.
It is known from [3] that every autoparallel submanifold of M is a totally geodesic submanifold and a submanifold 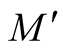 is autoparallel if and only if
is autoparallel if and only if 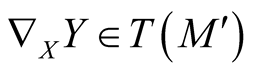 for any
for any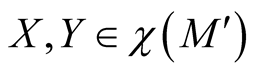 , where
, where  is the Riemannian connection of g.
is the Riemannian connection of g.
Theorem 1. Let 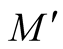 be a submanifold of a Riemannian manifold (M, g) and
be a submanifold of a Riemannian manifold (M, g) and 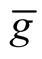 be the deformation of g on the normal tubular neighborhood
be the deformation of g on the normal tubular neighborhood 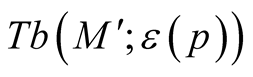 of
of 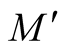 constructed above. Then
constructed above. Then 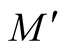 is a totally geodesic submanifold of
is a totally geodesic submanifold of .
.
Proof. For any point 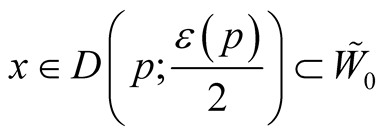 the functions
the functions 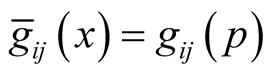 and
and 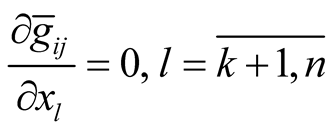 on
on
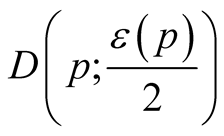 because the vector fields
because the vector fields 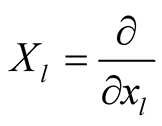 are tangent to
are tangent to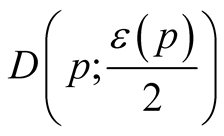 . By the formula of the Riemannian connection
. By the formula of the Riemannian connection 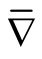 of the Riemannian metric
of the Riemannian metric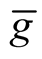 , [2] , we obtain for
, [2] , we obtain for 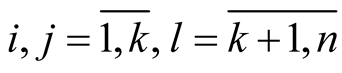
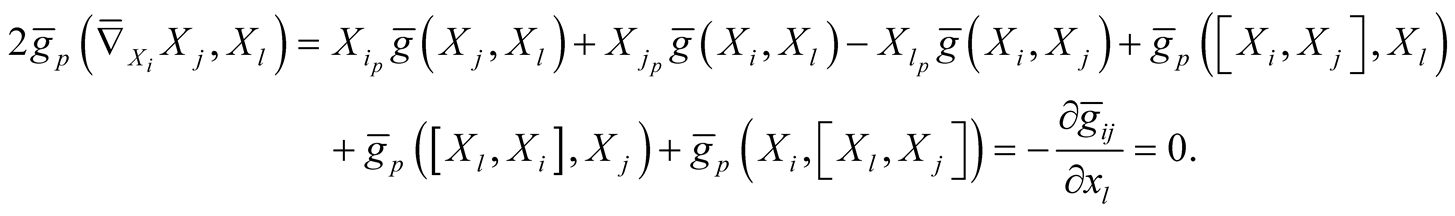 (1.1)
(1.1)
Here we use the fact that 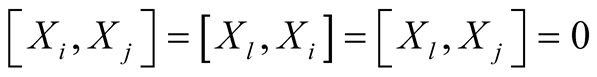 and that
and that 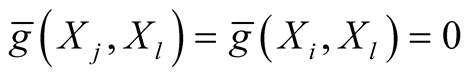 because
because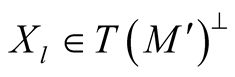 .
.
Thus,  and from the remarks above the theorem follows.
and from the remarks above the theorem follows.
QED.
Corollary 1.1. Let 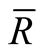 be the Riemannian curvature tensor field of
be the Riemannian curvature tensor field of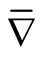 . Then
. Then 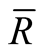 vanishes on every
vanishes on every
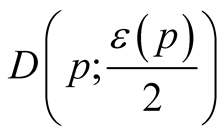 for
for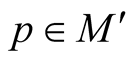 .
.
Proof. From the formula (1.1) it is clear that 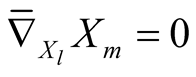 for
for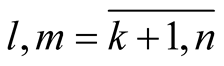 . The rest is obvious.
. The rest is obvious.
wang#title3_4:spQED.
2. Almost Hyper Hermitian Structures (ahHs) on Tangent Bundles
0˚. We follow especially close to [4] .
Let (M, g) be a n-dimensional Riemannian manifold and TM be its tangent bundle. For a Riemannian connection  we consider the connection map K of
we consider the connection map K of  [5] , [1] , defined by the formula
[5] , [1] , defined by the formula
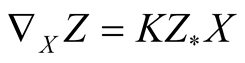 , (2.1)
, (2.1)
where Z is considered as a map from M into TM and the right side means a vector field on M assigning to 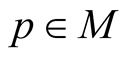 the vector
the vector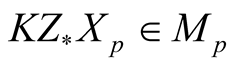 .
.
If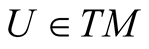 , we denote by HU the kernel of
, we denote by HU the kernel of 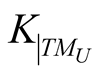 and this n-dimensional subspace of
and this n-dimensional subspace of 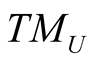 is called the horizontal subspace of
is called the horizontal subspace of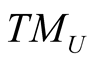 .
.
Let π denote the natural projection of TM onto M, then π* is a  -map of TTM onto TM. If
-map of TTM onto TM. If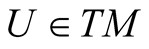 , we denote by VU the kernel of
, we denote by VU the kernel of 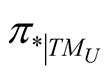 and this n-dimension subspace of
and this n-dimension subspace of 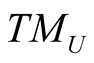 is called the vertical subspace of
is called the vertical subspace of
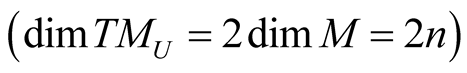
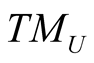 . The following maps are isomorphisms of corresponding vector spaces
. The following maps are isomorphisms of corresponding vector spaces 

and we have

If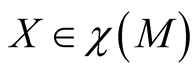 , then there exists exactly one vector field on TM called the “horizontal lift” (resp. “vertical lift”) of X and denoted by
, then there exists exactly one vector field on TM called the “horizontal lift” (resp. “vertical lift”) of X and denoted by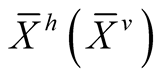 , such that for all
, such that for all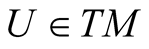 :
:
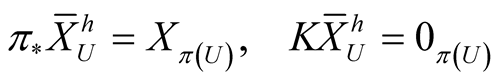 , (2.2)
, (2.2)
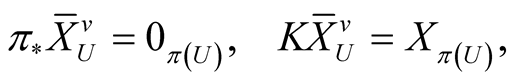 (2.3)
(2.3)
Let R be the curvature tensor field of , then following [5] we write
, then following [5] we write
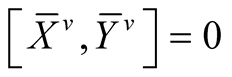 , (2.4)
, (2.4)
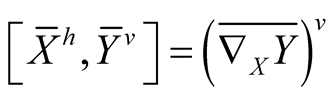 (2.5)
(2.5)
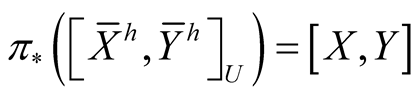 , (2.6)
, (2.6)
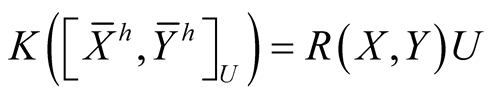 . (2.7)
. (2.7)
For vector fields 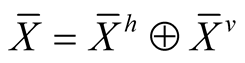 and
and 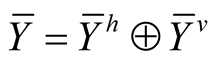 on TM the natural Riemannian metric
on TM the natural Riemannian metric 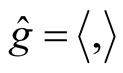 is defined on TM by the formula
is defined on TM by the formula
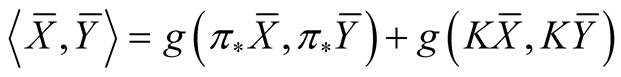 . (2.8)
. (2.8)
It is clear that the subspaces HU and VU are orthogonal with respect to .
.
It is easy to verify that  are orthonormal vector fields on TM if
are orthonormal vector fields on TM if  are those on M i.e.
are those on M i.e.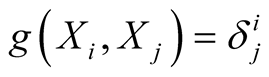 .
.
1˚. We define a tensor field J1 on TM by the equalities
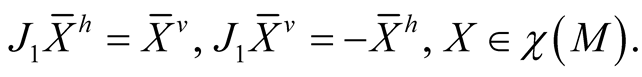 (2.9)
(2.9)
For 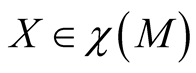 we get
we get

and
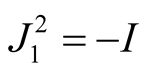 .
.
For 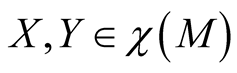 we obtain
we obtain
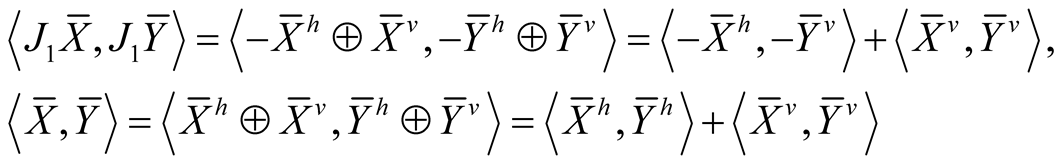
and it follows that 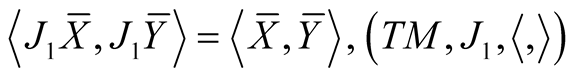 is an almost Hermitian manifold.
is an almost Hermitian manifold.
Further, we want to analyze the second fundamental tensor field h1 of the pair 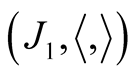 where h1 is defined by (2.11), [6] .
where h1 is defined by (2.11), [6] .
The Riemannian connection  of the metric
of the metric 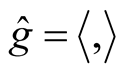 on TM is defined by the formula (see [1] )
on TM is defined by the formula (see [1] )
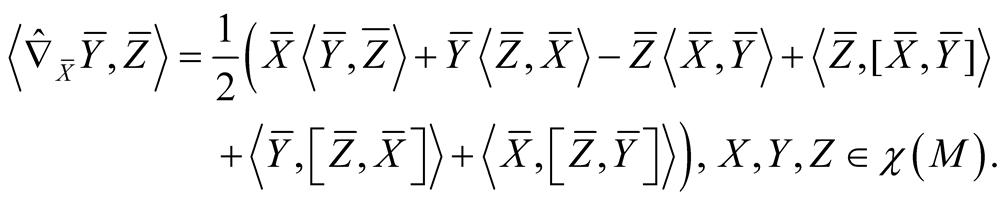 (2.10)
(2.10)
For orthonormal vector fields 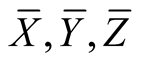 on TM we obtain
on TM we obtain
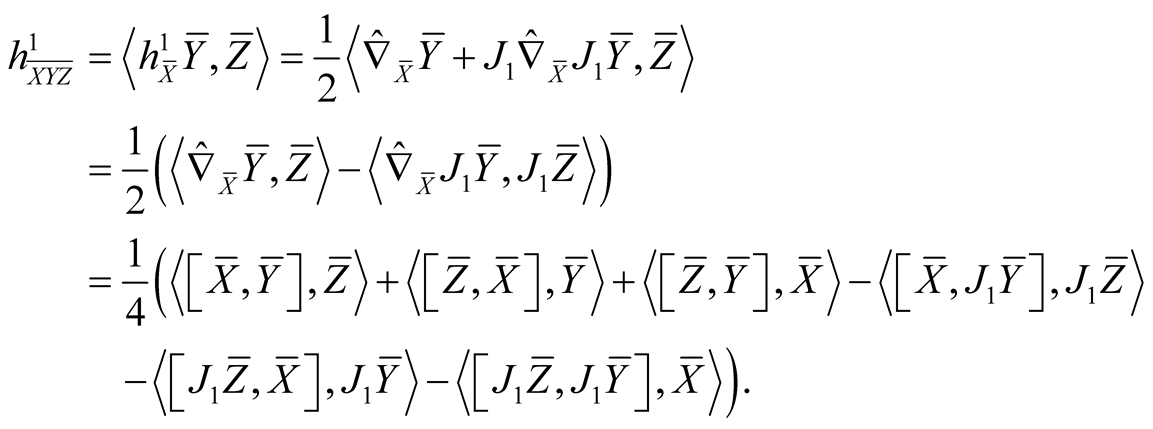 (2.11)
(2.11)
Using (2.4)-(2.7) and (2.11) we consider the following cases for the tensor field h1 assuming all the vector fields to be orthonormal.
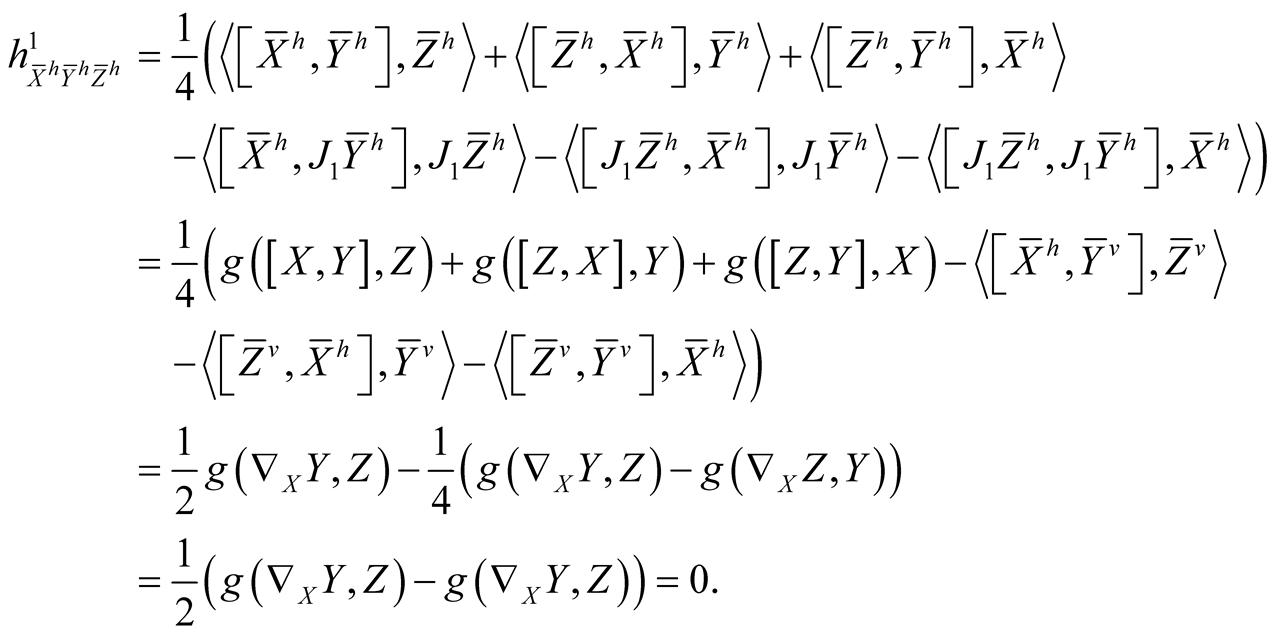 (1.1˚)
(1.1˚)
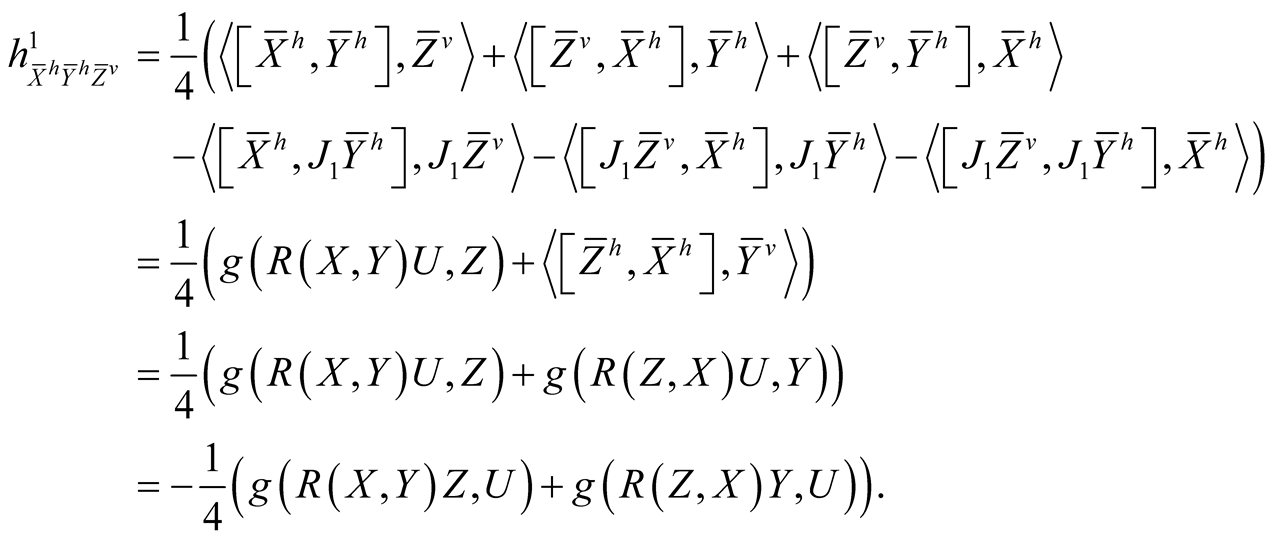 (2.1˚)
(2.1˚)
By similar arguments we obtain
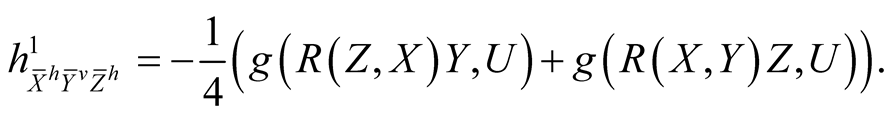 (3.1˚)
(3.1˚)
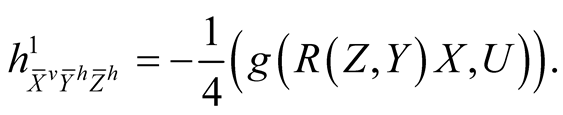 (4.1˚)
(4.1˚)
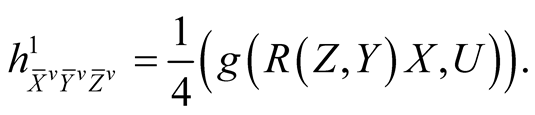 (5.1˚)
(5.1˚)
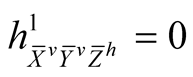 . (6.1˚)
. (6.1˚)
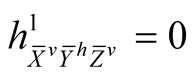 . (7.1˚)
. (7.1˚)
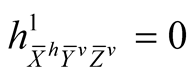 . (8.1˚)
. (8.1˚)
It is obvious that 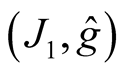 is a Kaehlerian structure if and only if
is a Kaehlerian structure if and only if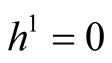 .
.
2˚. Now assume additionally that we have an almost Hermitian structure J on (M, g). We define a tensor field J2 on TM by the equalities
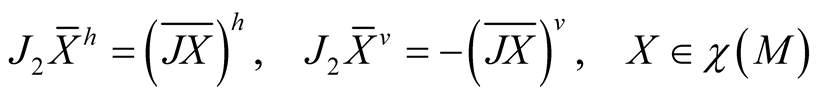 . (2.12)
. (2.12)
For 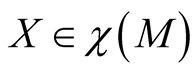 we get
we get
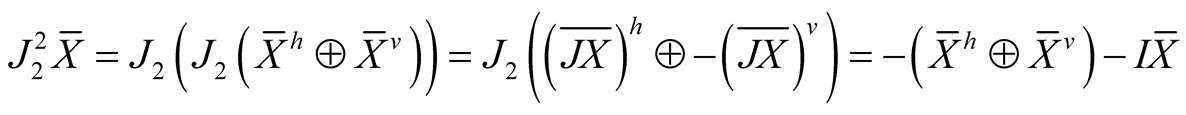
and
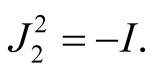
For  we obtain
we obtain

Further, we obtain


Thus, we get 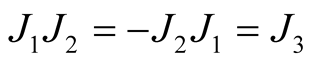 and ahHs
and ahHs 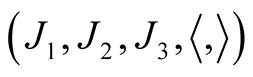 on TM has been constructed.
on TM has been constructed.
For orthonormal vector fields  on TM we obtain
on TM we obtain
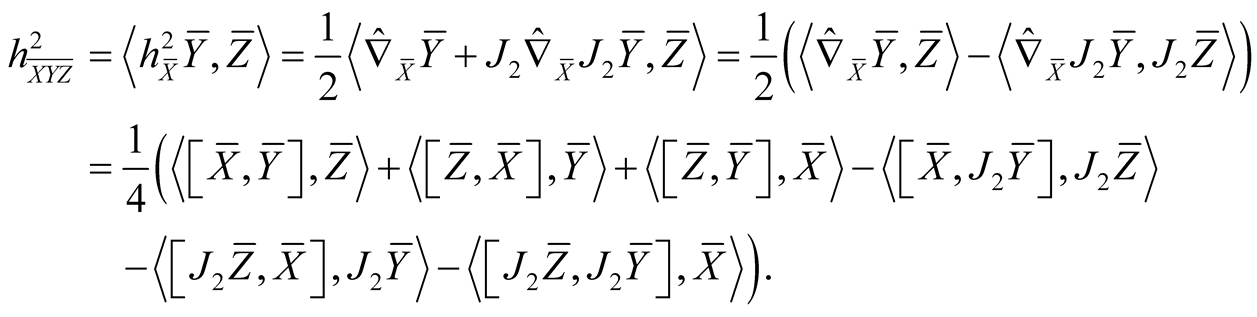 (2.13)
(2.13)
Using (2.4)-(2.7) and (2.13) we consider the following cases for the tensor field h2 assuming all the vector fields to be orthonormal.
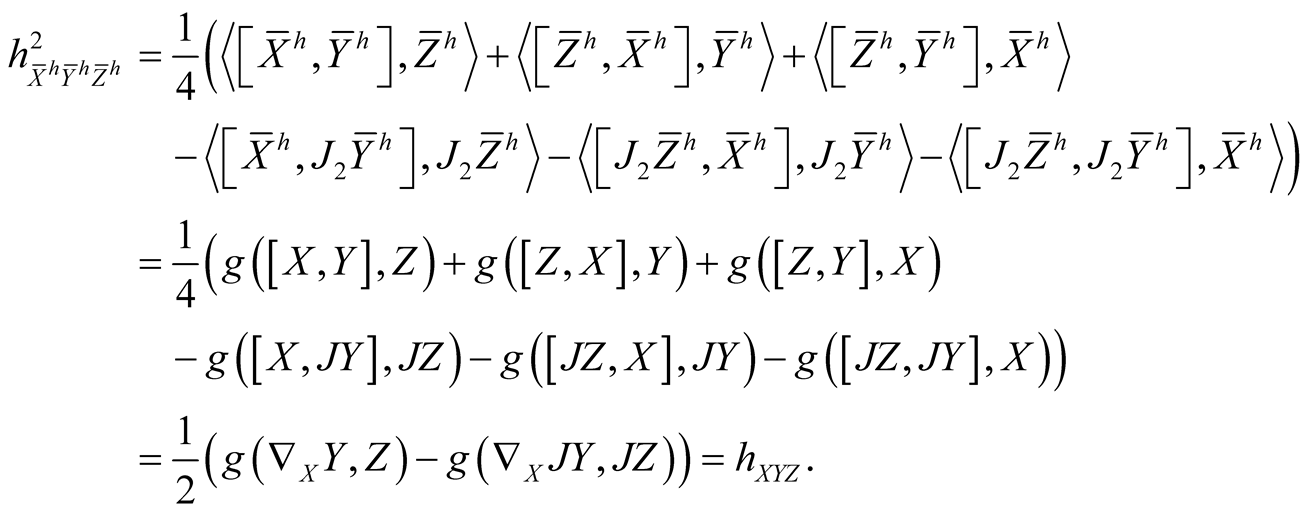 (1.2˚)
(1.2˚)
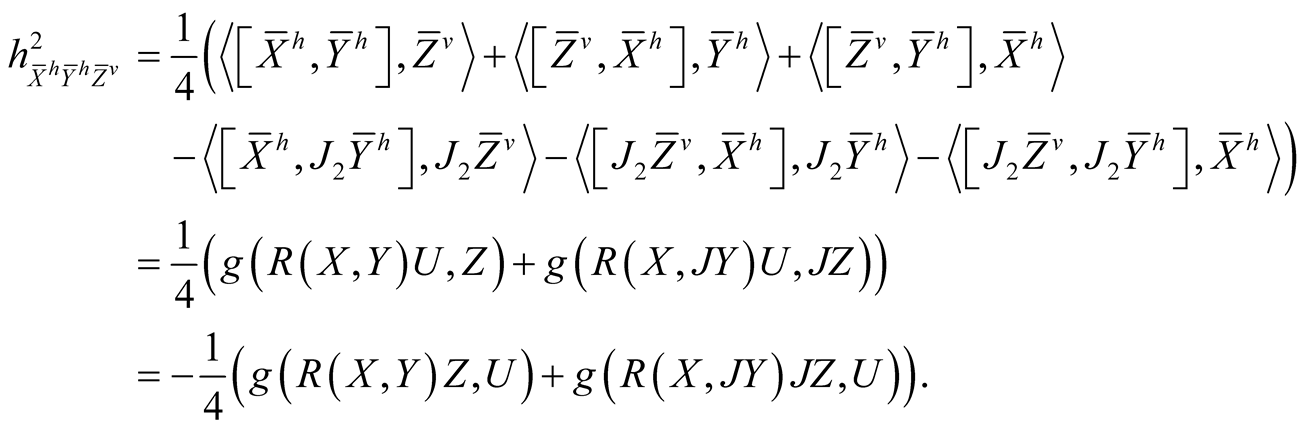 (2.2˚)
(2.2˚)
By similar arguments we obtain
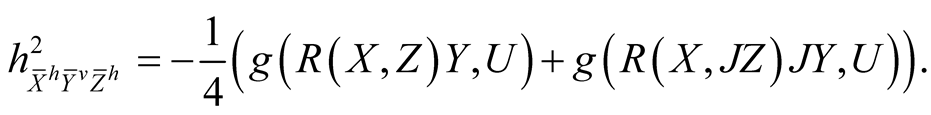 (3.2˚)
(3.2˚)
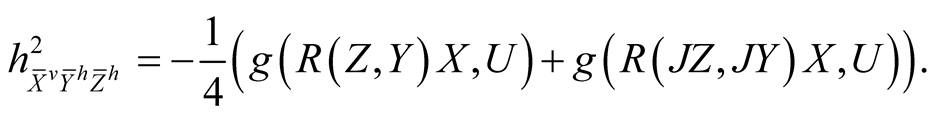 (4.2˚)
(4.2˚)
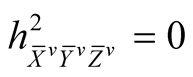 . (5.2˚)
. (5.2˚)
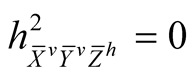 . (6.2˚)
. (6.2˚)
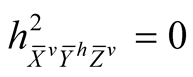 . (7.2˚)
. (7.2˚)
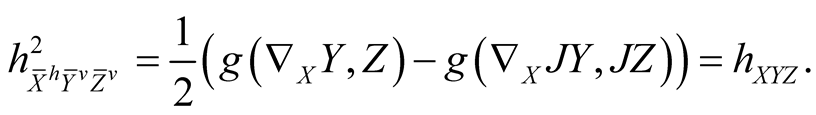 (8.2˚)
(8.2˚)
Here h is the second fundamental tensor field of the pair (J, g) on M.
3. Embeddings of Almost Hermitian Manifolds in Almost Hyper Hermitian Those
For an almost Hermitian manifold (M, J, g) we have constructed in Section 2 ahHs 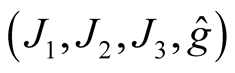 on TM. The manifold M can be considered as the null section OM in TM
on TM. The manifold M can be considered as the null section OM in TM  and it is clear from (2.8) that
and it is clear from (2.8) that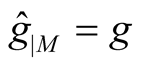 . All the results of 1 can be applied to a submanifold M in
. All the results of 1 can be applied to a submanifold M in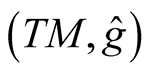 , see [7] . So, we can consider the normal tubular neighborhoods
, see [7] . So, we can consider the normal tubular neighborhoods 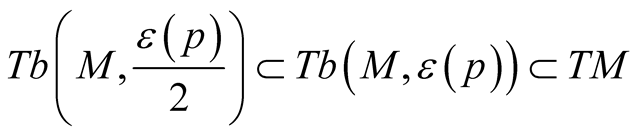 and the deformations
and the deformations 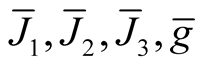 of the tensor fields
of the tensor fields 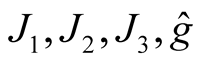 respectively.
respectively.
Theorem 2. Let (M, J, g) be an almost Hermitian manifold and 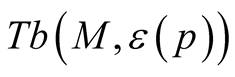 be the corresponding normal tubular neighborhood with respect to
be the corresponding normal tubular neighborhood with respect to 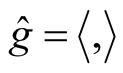 on TM. Then M(OM) is a totally geodesic submanifold of the almost hyper Hermitian manifold
on TM. Then M(OM) is a totally geodesic submanifold of the almost hyper Hermitian manifold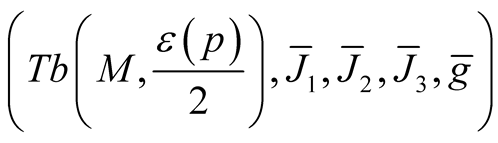 , where the ahHs
, where the ahHs 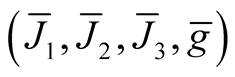 is the deformation of the structure
is the deformation of the structure 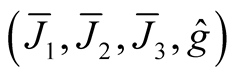 obtained in 2˚, Section 1. The structure
obtained in 2˚, Section 1. The structure 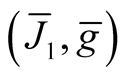 is Kaehlerian one.
is Kaehlerian one.
Proof. It follows from Theorem 1 that M is a totally geodesic submanifold of the Riemannian manifold
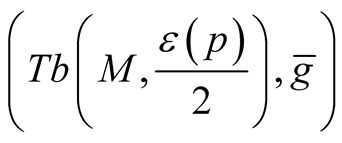 .
.
Let 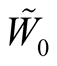 be a coordinate neighborhood in TM considered in 1˚, Section 1. A point
be a coordinate neighborhood in TM considered in 1˚, Section 1. A point 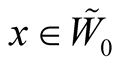 has the coordinates
has the coordinates 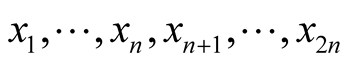 where
where 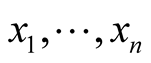 are coordinates of the point p in
are coordinates of the point p in 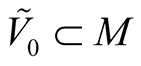 and
and 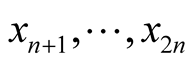 are normal coordinates of x in
are normal coordinates of x in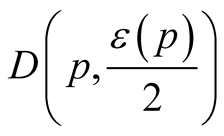 .
.
We denote 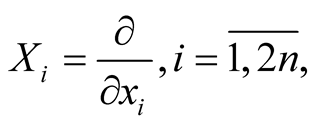
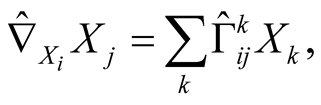
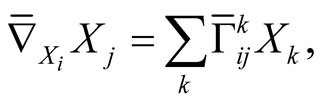
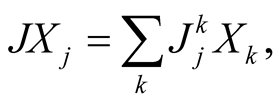


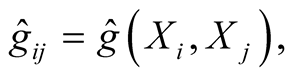 where
where  and
and 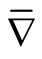 are Riemannian connections of metrics
are Riemannian connections of metrics  and
and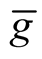 , J is any tensor field from
, J is any tensor field from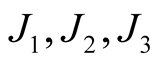 .
.
Using the construction in 2˚, Section 1 we have 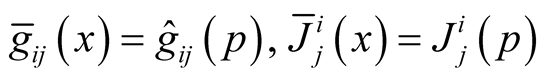 on
on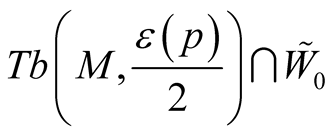 . According to [2] we can write
. According to [2] we can write
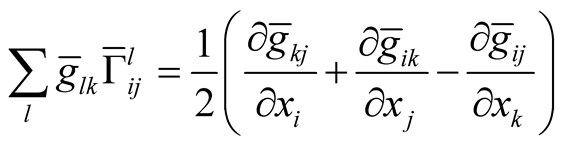 (3.1)
(3.1)
It follows from (3.1) that 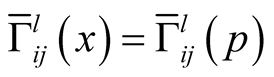 and
and 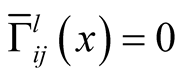 i.e.
i.e. 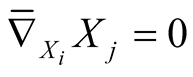 for
for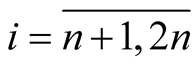 . Further, we get
. Further, we get
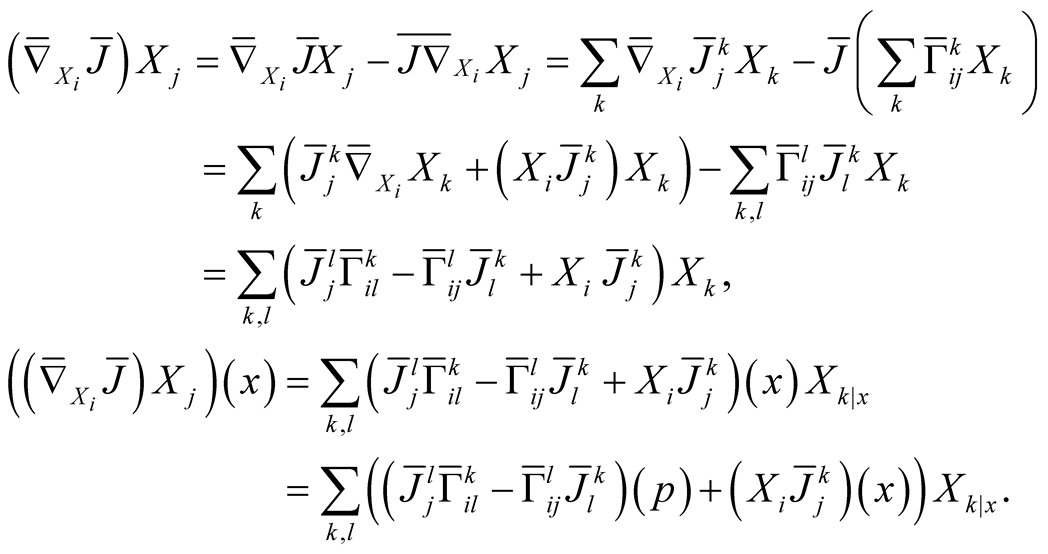
It follows that 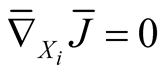 for
for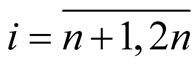 .
.
For 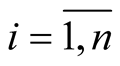
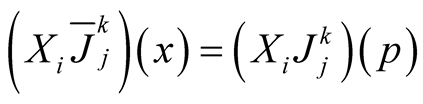 and we obtain
and we obtain
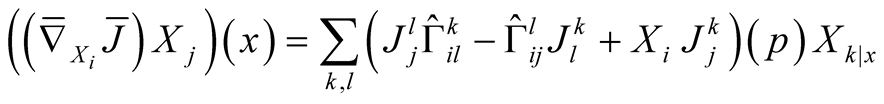 .
.
From the other side we can write
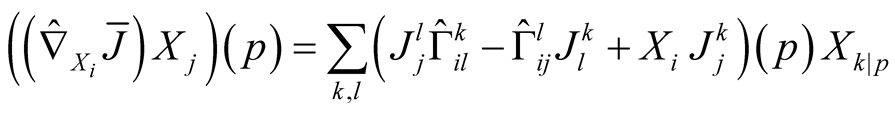 .
.
According to [6] we have 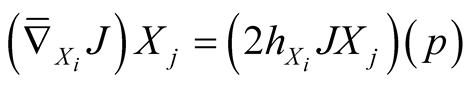 where the second fundamental tensor field h is defined by (2.11). From (1.1˚)-(8.1˚) it follows that
where the second fundamental tensor field h is defined by (2.11). From (1.1˚)-(8.1˚) it follows that 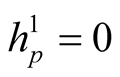 for any
for any . Thus, we have obtained
. Thus, we have obtained 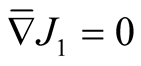 and the structure
and the structure  is Kaehlerian one on
is Kaehlerian one on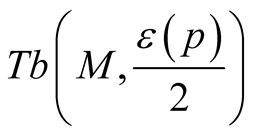 .
.
QED.
As a corollary we have got the following:
Theorem 3 [8] . Let (M, g) be a smooth Riemannian manifold and 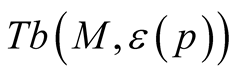 be the corresponding normal tubular neighborhood with respect to
be the corresponding normal tubular neighborhood with respect to 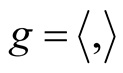 on TM. Then M(OM) is a totally geodesic submanifold of the Kaehlerian manifold
on TM. Then M(OM) is a totally geodesic submanifold of the Kaehlerian manifold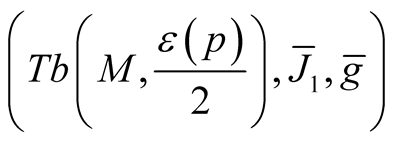 .
.
The classification given in [9] can be rewritten in terms of the second fundamental tensor field h (Table 1)

Table 1. Classification of almost Hermitian structures.
see chapter 5 of monograph [6] .
Let dimM ≥ 6 and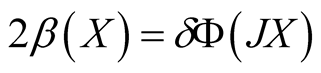 , where
, where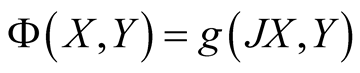 , then we have Table1
, then we have Table1
Proposition 4. Let (J, g) be from some class from the Table1 Then the structure 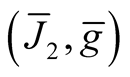 has the analogous class on
has the analogous class on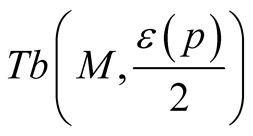 .
.
Proof. From (1.2˚)-(8.2˚) it follows that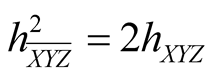 . The rest is obvious from the table.
. The rest is obvious from the table.
wang#title3_4:spQED.
4. Complex and Hypercomplex Numbers in Differential Geometry
For the manifold M we consider the products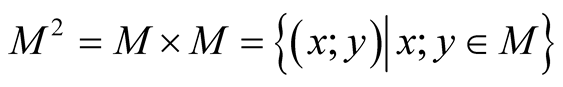 ,
,
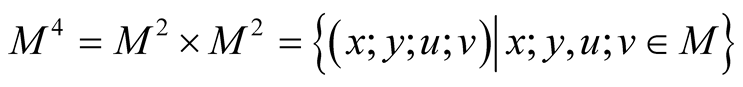 and the diagonals
and the diagonals ,
,
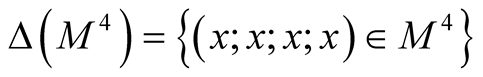 . It is obvious that the manifold
. It is obvious that the manifold 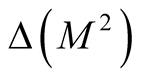 and
and 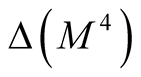 are diffeomorphic to M
are diffeomorphic to M
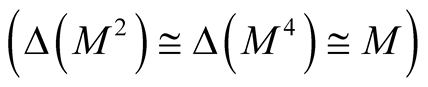 .
.
Theorem 5 [1] . Let (M, ) be a manifold with a connection
) be a manifold with a connection  and π: TM → M be the canonical projection. Then there exists such a neighborhood N0 of the null section OM in TM that the mapping
and π: TM → M be the canonical projection. Then there exists such a neighborhood N0 of the null section OM in TM that the mapping

is the diffeomorphic of N0 on a neighborhood 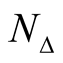 of the diagonal
of the diagonal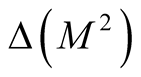 .
.
Further,  is a Riemannian connection of the Riemannian metric g. Combining the Theorems 3 and 5 we have obtained the following.
is a Riemannian connection of the Riemannian metric g. Combining the Theorems 3 and 5 we have obtained the following.
Theorem 6. The diffeomorphism φ induces the Kaehlerian structure 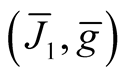 on the neighborhood
on the neighborhood 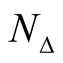 of the diagonal
of the diagonal 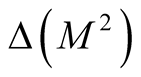 and
and 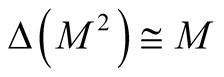 is a totally geodesic submanifold of the Kaehlerian manifold
is a totally geodesic submanifold of the Kaehlerian manifold 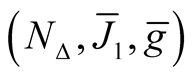 .
.
Remark. Generally speaking, the complex structure of the Kaehlerian manifold 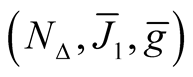 is not compatible with the product structure of M2. It means that if
is not compatible with the product structure of M2. It means that if 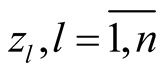 are the complex coordinates of a point
are the complex coordinates of a point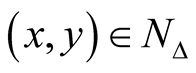 , then, generally speaking, we can not find such real coordinates
, then, generally speaking, we can not find such real coordinates 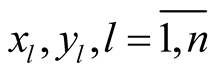 of the points
of the points 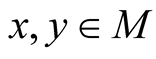 respectively that
respectively that 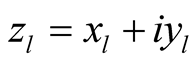 where
where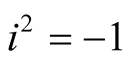 .
.
Combining the Theorems 2, 3, 4, 5 and 6 we have obtained the following.
Theorem 7. There exists the hyper Kaehlerian structure 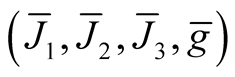 on a neighborhood
on a neighborhood 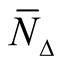 of the diagonal
of the diagonal 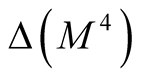 and
and 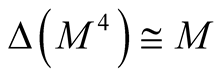 is a totally geodesic submanifold of the hyper Kaehlerian manifold
is a totally geodesic submanifold of the hyper Kaehlerian manifold
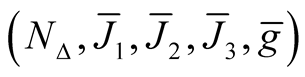 .
.
Remark. Generally speaking, the hypercomplex structure of the hyper Kaehlerian manifold  is not compatible with the product structure of M4. It means that if
is not compatible with the product structure of M4. It means that if  are the hypercomplex coordinates of a point
are the hypercomplex coordinates of a point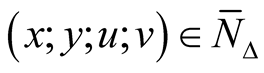 , then, generally speaking we can not find such real coordinates
, then, generally speaking we can not find such real coordinates
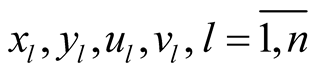 of the points x; y; u;
of the points x; y; u; 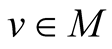 respectively that
respectively that 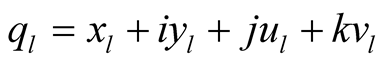 where i2 = j2 = k2 = –1, ij = –ji = k.
where i2 = j2 = k2 = –1, ij = –ji = k.
5. A Local Construction of Kaehlerian and Riemannian Metrics
1˚. We consider a Riemannian manifold (M, g) as a totally geodesic subanifold of the Kaehlerian manifold
 (see Theorem 3) then
(see Theorem 3) then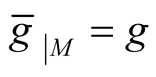 .
.
Let 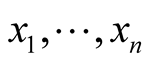 be coordinates in some coordinate neighborhood
be coordinates in some coordinate neighborhood 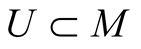 and
and 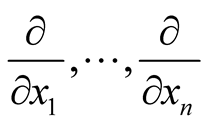 be the corresponding vector fields. We can choose a neighborhood
be the corresponding vector fields. We can choose a neighborhood 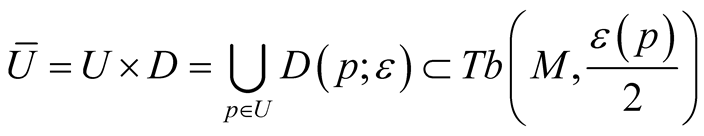 where
where 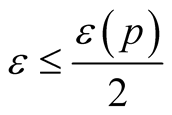 for every point
for every point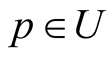 . It is clear from 3o, 1 that
. It is clear from 3o, 1 that 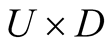 is a Riemannian product with respect the metric
is a Riemannian product with respect the metric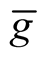 . For every point
. For every point 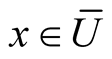 where
where 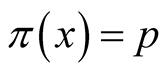 we denote
we denote 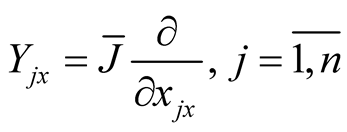 and the vector fields
and the vector fields 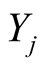 define the coordinates
define the coordinates 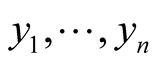 on
on  hence
hence 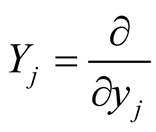 is tangent to
is tangent to  for
for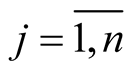 .
.
So, 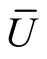 is an coordinate neighborhood of the Kaehlerian manifold
is an coordinate neighborhood of the Kaehlerian manifold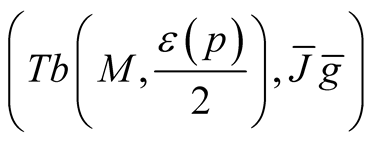 , with complex coordinates
, with complex coordinates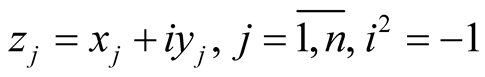 , and the vector fields
, and the vector fields 
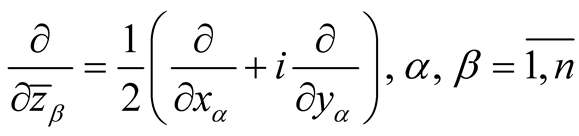 . It is known [3] that the Kaehlerian metric
. It is known [3] that the Kaehlerian metric 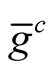 has on
has on 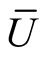 the following decomposition
the following decomposition
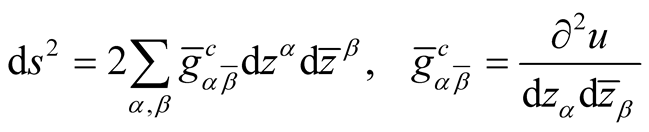 where u is a real-valued function on
where u is a real-valued function on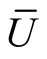 .
.
We have
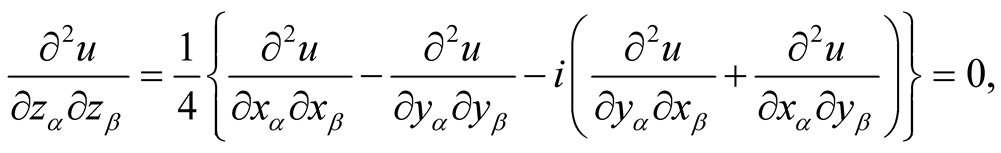
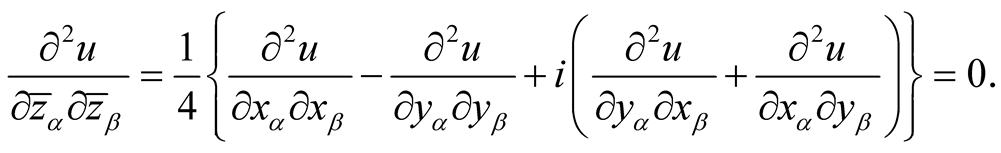
It follows that
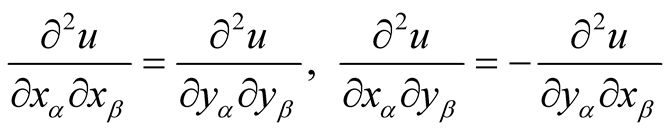 .
.
Further, we obtain


Finally, we get

We can consider the restriction of 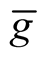 and the function u on the neighborhood U. So, we have obtained.
and the function u on the neighborhood U. So, we have obtained.
Theorem 8. Let (M, g) be a Riemannian manifold and 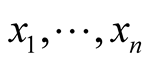 be coordinates is some coordinate neighborhood
be coordinates is some coordinate neighborhood . There exists a smooth function u:
. There exists a smooth function u:  that
that 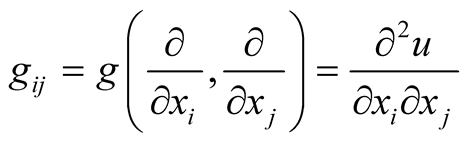 on U.
on U.
2˚. Let (M, J, g) be a Kaehlerian manifold ,
, 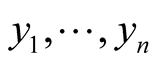 , be coordinates is some coordinate neighborhood
, be coordinates is some coordinate neighborhood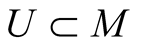 , where
, where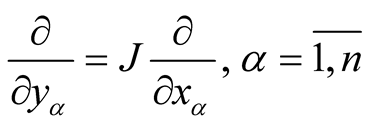 . We consider a function u:
. We consider a function u:  from Theorem 5. Then, we have the following conditions on this function.
from Theorem 5. Then, we have the following conditions on this function.
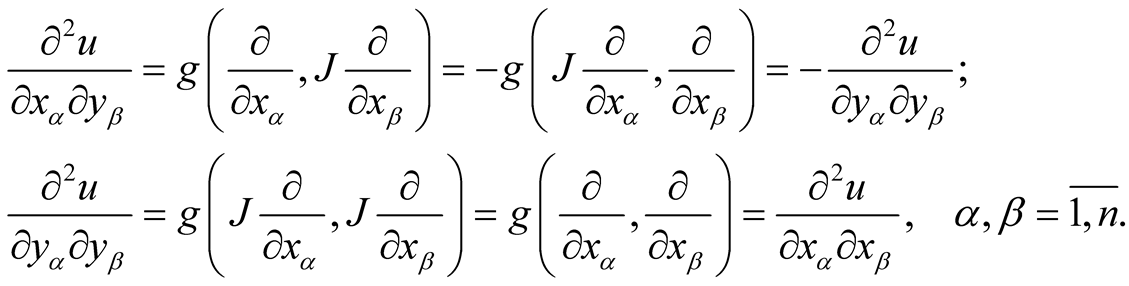
6. Conclusion
We consider such mappings in the category of Riemannian manifolds that metrics are invariant with respect to them. It follows that only totally geodesic submanifolds are “naturally good”. Theorems 6 and 7 allow considering any Riemannian manifold as a totally geodesic submanifold of a Kaehlerian (hyper Kaehlerian) one i.e. to apply the results of Kaehlerian (hyper Kaehlerian) geometry to Riemannian metrics. We remark that Whitnies embeddings are not suitable in this context.