A Trapezoidal-Like Integrator for the Numerical Solution of One-Dimensional Time Dependent Schrödinger Equation ()
1. Introduction
Numerical methods have played an important role in researches in physics. Most often Partial Differential Equations (PDEs) are used to model physical problems. Proficiency in the numerical approach to the solution of PDEs is a great tool in the hand of a mathematical physicist. According to [1] , numerical methods of PDEs have played an important role in various areas of mathematical physics. In numerical relativity a set of highly nonlinear systems of coupled differential equations of general relativity have to be solved under very general symmetry conditions in order to predict the profile of gravitational waves expected to be observed by ground-based gravitational wave detectors. In Euler’s equation, the hydro-dynamical equations are solved by numerical methods in order to explain and predict astrophysical phenomena. In the evolution of a Bose condensate, the solution of the time dependent Schrodinger equation involved is sought for by numerical method.
Schrodinger equation has a wide range of application in physics varying from optics, propagation of electric field in optical fibers, self-focusing and self-modulation of trains in monochromatic wave in nonlinear optics, collapse of Langmuir waves in plasma physics as well as modeling of deep water freak waves in ocean [2] -[4] . Reference [5] , used the Schrodinger equation in modeling the 2004 Indonesian Tsunami while [6] used the Schrodinger equation in studying Bose-Einstein condensation using ultra cold neutral bosonic gases. Reference [7] used the Schrödinger wave equation in explaining the quantum behavior of a conventional wireless communication system. There exists therefore, the need for further researches seeking more accurate numerical approximations to the Schrödinger equation.
In this paper, we shall discretize the 1-dimensional Schrödinger equation by the Method of Lines (MOL). The numerical solution of the resulting system of coupled stiff Ordinary Differential Equations (ODEs) shall be sought for using an L-stable implicit trapezoidal-like integrator. This paper is organized as follows. In Section 2 we give a brief overview of the MOL. In Section 3 we discretize the 1-dimensional time dependent Schrödinger equation by the MOL under some assumptions. In Section 4 we discuss the stability property of the trapezoidal- like integrator. In Section 5 we show how absolute and relative errors are obtained in the computation and in Section 6 we discuss the results obtained.
2. The Method of Lines
A well-known numerical approach for solving a time dependent PDE, whose solutions vary both in time and in space, is the Method of Lines. In the Method of Lines approach to the solution of PDEs, the solution of the PDE is sought for in a finite domain with a time coordinate t and a spatial coordinate, x. The spatial coordinate is defined as a discrete set of points given by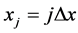 , and the boundaries correspond to the points
, and the boundaries correspond to the points 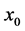 and
and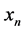 . Time,
. Time, 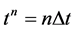 is also defined only for certain values of the continuum time. Thus a function
is also defined only for certain values of the continuum time. Thus a function 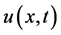 is defined only for the values of x and t that correspond to points
is defined only for the values of x and t that correspond to points 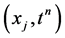 in the mesh by
in the mesh by . For a uniformly discretized domain,
. For a uniformly discretized domain, 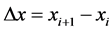 and
and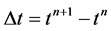 , indicate the resolution in the spatial and time coordinates respectively. In using the MOL to solve PDEs the spatial derivative is approximated by its finite difference approximation thereby, generating a coupled system of Ordinary Differential Equations (ODEs) in the time dependent variable t, which is associated with the initial value. Numerical approximations to the solutions of the PDE are obtained by marching forward in time on the grid. It is at this point that existing and generally well established numerical methods for initial value ODEs can be used to compute numerical solutions to the PDE. In [8] , the applicability of the MOL in solving problems in Physics, fluid dynamics, rector models as well as automatic control is demonstrated.
, indicate the resolution in the spatial and time coordinates respectively. In using the MOL to solve PDEs the spatial derivative is approximated by its finite difference approximation thereby, generating a coupled system of Ordinary Differential Equations (ODEs) in the time dependent variable t, which is associated with the initial value. Numerical approximations to the solutions of the PDE are obtained by marching forward in time on the grid. It is at this point that existing and generally well established numerical methods for initial value ODEs can be used to compute numerical solutions to the PDE. In [8] , the applicability of the MOL in solving problems in Physics, fluid dynamics, rector models as well as automatic control is demonstrated.
Discretization of the Schrödinger Equation by the MOL
Given the Schrödinger equation
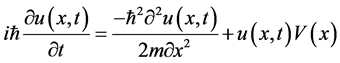 (1)
(1)
where:
 is complex dependent variable;
is complex dependent variable;
x is a boundary-value (spatial) independent variable;
t is initial-value independent variable;
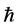 is Planck constant;
is Planck constant;
i is an imaginary complex number .
.
According to [9] , by letting 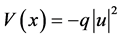 and normalizing
and normalizing 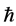 and 2m to unity Equation (1), can be written in the form
and 2m to unity Equation (1), can be written in the form
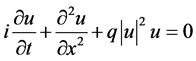 (2)
(2)
where q is arbitrary parameter.
In subscript notation Equation (2) can be written as
![]() (3)
(3)
Replacing the spatial derivative ![]() by a second order finite difference approximation in Equation (3) and following [10] , the function,
by a second order finite difference approximation in Equation (3) and following [10] , the function, ![]() , is replaced by the sum of its real part
, is replaced by the sum of its real part ![]() and its imaginary part
and its imaginary part ![]() in the form
in the form
![]() (4)
(4)
Substituting Equation (4) into Equation (3), the two equations:
![]() (5a)
(5a)
or
![]() (5b)
(5b)
are obtained.
Equating the real and imaginary parts of Equations (5a) and (5b) to zero, the following nonlinear system of PDE
![]() (6a)
(6a)
![]() (6b)
(6b)
is obtained.
From Equation (6a) the equations:
![]() (7a)
(7a)
or
![]() (7b)
(7b)
are obtained.
From Equation (6b),
![]() (8a)
(8a)
or
![]() (8b)
(8b)
are obtained.
Replacing the second order partial derivative ![]() in Equation (7b) by the three point central difference approximation
in Equation (7b) by the three point central difference approximation ![]() and to the replacing the second order partial derivative
and to the replacing the second order partial derivative ![]() by its equivalent three point central difference approximation
by its equivalent three point central difference approximation ![]() in Equation (8b) where h is the space between the discretized line and n is the number of grids, the following equations are obtained.
in Equation (8b) where h is the space between the discretized line and n is the number of grids, the following equations are obtained.
![]() (9a)
(9a)
![]() (9b)
(9b)
According to [11] , the analytical solution of Equation (3) is
![]() (10)
(10)
To analyze ![]() as two real functions it is obtained that
as two real functions it is obtained that
![]() (11)
(11)
Equations (9a) and (9b) constitute the discretized form of the real and imaginary parts of Equation (3) by the MOL respectively. The real and the imaginary parts of the solution of the Schrodinger equation are independent, identically distributed standard normal random variables with mean 0 and variance 1 [12] . Hence Equation (9a) or (9b) can be chosen for computational purposes. In this paper we shall use Equation (9a) and![]() , for the numerical integration.
, for the numerical integration.
3. L-Stable Implicit Trapezoidal-Like Integrator
The trapezoidal-like integrator
![]() (12)
(12)
shall be used in the numerical integration, where:
![]() (13a)
(13a)
![]() (13b)
(13b)
![]() are the first and second eigenvalues of the discretization matrix respectively; l is the time step; and
are the first and second eigenvalues of the discretization matrix respectively; l is the time step; and ![]() denotes differentiation with respect to time.
denotes differentiation with respect to time.
The derivation of the method (12) and the analysis of the order of accuracy are as discussed in [13] .
3.1. Stability Properties of the Method (12)
In this section, we state and prove one lemma and two theorems which relate to the stability property of the method (12) as follows:
3.1.1. Lemma 1
Let ![]() and
and ![]() be the eigenvalues of the system of ODE evolved by discretizing the Schrödinger equation by the MOL; and let
be the eigenvalues of the system of ODE evolved by discretizing the Schrödinger equation by the MOL; and let ![]() and
and![]() . Suppose the following conditions hold:
. Suppose the following conditions hold:
1) ![]() if
if ![]() and
and
2) ![]() if
if ![]()
Then, in Equation (12),![]() .
.
Proof.
Given that ![]() if
if ![]() and
and ![]() if
if ![]()
![]() and
and![]() .
.
But ![]() and
and![]() ; given.
; given.
![]() and
and![]() .
.
But
![]() and
and![]() .
.
Hence
![]() (13)
(13)
![]() All the quantities on the L.H.S. of inequality (13) are positive.
All the quantities on the L.H.S. of inequality (13) are positive.
Expanding and rearranging the L.H.S. of (13), we have
![]() . (14)
. (14)
Dividing inequality (14) through by ![]() yields
yields
![]() . (15)
. (15)
Therefore,
![]() . (16)
. (16)
Resolving inequality (16) into partial fractions, we have
![]() . (17)
. (17)
From Equations (17), (13a) and (13b), we have that![]() .
.
This proves the Lemma 1.
3.1.2. Theorem 1
The numerical integrator (12) is A-stable.
Proof.
Applying the test equation
![]() . (18)
. (18)
To the method in Equation (12) and from the general linear multistep method.
The Schur’s polynomial is thus given by
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
By Schur’s condition
![]() (21)
(21)
Hence
![]()
![]()
![]()
![]() (23)
(23)
But ![]() as proved in Lemma 1, hence
as proved in Lemma 1, hence ![]()
The numerical integrator (12) is therefore A-stable.
3.1.3. Theorem 2
The numerical integrator is L-stable.
Substituting the scalar test Equation (18) into Equation (12) yields
![]() (24)
(24)
![]() (25)
(25)
![]() (26)
(26)
Hence
![]() (27)
(27)
Substituting for R and S in Equation (27), simplifying and taking the limit by use of L’Hospital’s rule we obtain
![]() (28)
(28)
Hence, the proof of the Theorem 2. Thus the integrator (12) is L-stable.
4. Computation of Absolute and Relative Errors
In this section we explain how the absolute and relative errors of the methods shown in the Table 1 and Table 2 were obtained.
4.1. Absolute Errors
The absolute errors of the scheme were computed by the use of the formula:
![]()
where the numerical solution at the grid point ![]() is
is ![]() and the analytical solution at the same grid point is
and the analytical solution at the same grid point is ![]()
4.2. Relative Errors
Relative errors of the method were computed by use of the formula:
![]()
Table 1. Absolute errors of the trapezoidal-like method at various spatial discretization levels.
![]()
where the numerical solution at the grid point ![]() is
is ![]() and the analytical solution at the same grid point is
and the analytical solution at the same grid point is ![]()
5. Results and Discussion
On the implementation of the L-stable implicit trapezoidal-like integrator for the solution of one-dimensional time dependent Schrödinger equation after discretizing with the MOL, the errors and relative errors of the scheme were computed as shown in Table 1 and Table 2 respectively. The L-stable property of the scheme is supported by the fact that the maximum relative errors at the various discretization levels are not significantly different as shown in Table 3. The performance of the trapezoidal-like integrator compares favorably with the
![]()
Table 2. Relative errors of the trapezoidal-like method at various spatial discretization levels.
![]()
Table 3. Maximum relative errors of the trapezoidal-like integrator at various spatial discretization levels.
![]()
Table 4. Comparison of the relative maximum errors of the trapezoidal-like integrator and [10] at various spatial discretization levels.
method of [10] as shown in Table 4. This indicates that the method is considered to give more accurate and stable results at the various spatial discretization levels considered. All computations and plotting of Figure 1 and Figure 2 in this paper were carried out using Maple 15.
NOTES
*Corresponding author.