Equity Pricing and Risk Premium under Long-Run Risks and Incomplete Information ()
1. Introduction
One of the fundamental challenges in theoretical finance is obtaining an adequate model of the equity premium. Given observed post-war data, the power utility function, e.g., implies a risk-averse agent must have relative risk aversion γ > 50. The result suggests that the risk aversion should be an order of magnitude higher than the one implied by independent estimates (Friend and Blume [1] ). Alternatively, under the observed risk premium, investors should dramatically leverage the investment of their wealth in the stock market beyond current levels (Cochrane [2] , Chapter 21).
One recent approach to this problem is the long-run risks (LRR) model first developed by Bansal and Yaron [3] (BY later). In the LRR model, current shocks to expected growth have a persistent effect on the expectations about consumption and dividend growth. In equilibrium, investors exposed to the risk require higher premium for holding equities. BY form the LRR model based on Epstein and Zin [4] recursive preferences.
In the current paper we retain the LRR feature that the latent conditional consumption mean is one of the determinants of the risk premium but extends the model to include learning about the latent state. Eraker [5] also extends LRR model in two new ways. First, he introduces jumps into the economic uncertainty in consumption growth. Second, to resolve the negatively sloped yield curve problem of LRR models, he derives a nominal term structure of interest rates assuming that the conditional mean of inflation is negatively correlated with consumption and dividend growth. Under these assumptions, Eraker is able to produce reasonable equity premium levels and positively sloped nominal yield curve. However, that requires the levels of risk aversion and the elasticity of intertermporal substitution (EIS) of at least 8 and 5, respectively. Our model can also fit equity premium but regardless of EIS level if we introduce learning about the latent state variable.
Our work in this paper complements Eraker [5] . In LRR models and in Eraker’s model, the long-run risk component is observed by investors. However, in reality, this is not the case. Investors have to learn the value of conditional consumption mean based on information available to them. To this end, we model how investors learn about the latent variable. We assume that investors build a minimum mean square estimate of the latent state variable from observations on consumption and dividend growth. The solution of this optimal filtering problem allows us to derive the processes for the state variables under a new probability measure corresponding to information available to investors. We show that there are closed form solutions for equity prices and equity premium under this new risk-neutral measure1.
Abstracting from other modeling features that can also contribute to the explanation of the equity premium, we focus on the contribution of uncertainty associated with learning about the latent consumption mean. Our model is related to Jacoby, Paseka, and Wang [6] (JPW later), who also study the impact of learning on the asset price dynamics and the equity premium. There are several differences, however, that make our model distinctly different from that in JPW [6] . JPW [6] adopt the framework of Bakshi and Chen [7] (BC later) in which asset valuation is earnings-based rather than dividend-based allowing them to value even firms that do not pay dividends2. Earnings growth is modeled as a stochastic process with an unobserved mean, itself a mean-reverting random process. In order to value assets both JPW [6] and BC [7] assume an exogenous pricing kernel process. Unlike BC [7] and JPW [6] , we adopt LRR model so that the pricing kernel is endogenous, the result of agent optimization problem in equilibrium. The obvious consequence of this modeling contrast is that prices of risk in our model are all endogenous whereas those in BC [7] and JPW [6] are exogenously specified and need to be estimated from the data. As a result, our modeling approach being more parsimonious affords fewer degrees of freedom and is potentially less subject to concerns about overfitting once the model is brought to the data. Equity premium in BC [7] comes from contributions of the variation in three state variables: earnings growth, mean of earnings growth, and the short rate. In contrast, in JPW [6] , the posterior estimate (by representative agents) of shocks to the mean of earnings growth is a deterministic function of the shocks to earnings growth because agents are assumed to use the latter as the only source of information in their learning exercise. This modeling assumption is reflected in the equity premium in JPW [6] . There are only two independent contributions to the equity premium from variation in earnings growth and from that in the short rate. However, the former contribution is amplified by the fact that there is an extra uncertainty due to sampling variation in the posterior estimate of the mean of earnings growth. The impact of learning on equity premium in JPW [6] is thus only through the correction to the equity premium contribution from the variation in earnings growth. The risk premium due to the variation of the short rate is not affected by learning. In our model, however, because the pricing kernel is affected by learning in equilibrium, uncertainty about unobserved conditional mean of consumption growth affects all contributions to the equity premium.
Further, both BC [7] and JPW [6] assume an exogenous short rate process. In contrast, in our model short rate is determined endogenously from the drift of the stochastic discount factor. In fact, the model implies that the short rate inherits the mean-reverting property of the posterior estimate of the conditional consumption mean.
We analyze an example of equity valuation model based on our LRR incomplete-information pricing kernel. We calibrate the model to data on aggregate consumption and dividends as well as earnings-per-share on a CRISP value-weighted index. Based on calibrated parameters we then compute model-implied price-earnings ratio, equity premium, and the risk free rate. We pay special attention to the composition of equity premium. The largest portion of the premium is predominantly due to the hedging demand induced by the variation in earnings growth, with more minor contributions from hedging demands due to the mean of earnings growth and the short rate. We also note that inference environment is essential for empirical performance of the model. Learning is easier if observed processes—consumption and dividend growth—have higher (in absolute value) correlations with the latent process. In that case, the model can fit equity premium even at higher values of the persistence in the latent process, thus, revealing a trade-off between learning and persistence of the latent conditional consumption mean. To explore this further, we consider two cases. In the first case of relatively small values of the speed of mean reversion (persistence) in the conditional mean of consumption growth, the contribution of earnings risk to the risk premium is: 7%. Variation in the mean of earnings growth contributes substantially lower amount to the risk premium, mostly due to low elasticity of asset prices to mean earnings growth. However, its contribution is far from negligible, amounting to 4%. Variation in the short rate (equivalently, in the latent conditional mean of consumption growth) is the last contributing factor. However, its contribution to the equity premium is negative and largely negates the contribution of the mean earnings growth. In the second case of larger values of the speed of mean reversion in the conditional mean of consumption growth, the model matches relatively well to the data on the levels of price/earnings ratio, risk premium, and the short term risk free rate.
Despite the encouraging outcome of the calibration exercise, we note that in the current form the relation between price-earnings ratio and the risk premium is complex. In the first case, the relation between the two is negative (larger risk premiums imply smaller price-earnings ratios). However, in the second case the relation is positive, with higher price-earnings ratios corresponding to higher risk premiums. It appears that the influence of learning on the equilibrium pricing kernel—a feature absent in previous work—at least partially decouples instantaneous risk premium from price-earnings ratios implying, in general, a non-monotonic relation.
The rest of the paper is organized as follows. In section 2 we state the assumptions of the model, derive the optimal posterior estimate of the latent conditional mean of consumption growth, and solve for the value function jointly with learning problem. Further, in section 3 we derive the pricing kernel (stochastic discount factor) with adjustment for learning. In section 4 we introduce an equity valuation example and apply our pricing kernel to computing price-earnings ratio, equity premium, and the short rate. We also calibrate the model to data on aggregate consumption and dividends as well as earnings per share on a CRISP value-weighted index. Finally, we conclude in section 5. We refer the reader to Appendix for derivations of all necessary results in the paper.
2. Long-Run Risk Model with Learning
We use BY [3] economy as our starting point. We retain main features of models by BY [3] and Eraker [5] such as recursive preferences and non-i.i.d. consumption and dividend growth. We list the assumptions below.
Assumption 1 Following Eraker [5] , we model the processes of consumption growth and dividend growth with drift being linear function of the persistent long-run risk component :
:
 (1)
(1)
 (2)
(2)
where wc and wd are standard Wiener processes,  , and V is conditional instantaneous variance of consumption growth.
, and V is conditional instantaneous variance of consumption growth.
Assumption 2 The conditional mean of consumption growth is not observed by agents. They only know that it follows a mean reverting process with zero long-run mean:
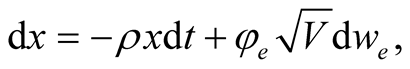 (3)
(3)
where  are standard Wiener processes,
are standard Wiener processes, 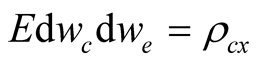 and
and .
.
Assumption 3 We assume that all state variable processes are homoscedastic, i.e., 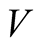 is constant over time.
is constant over time.
We make the last assumption to retain the closed form solution for our equity pricing exercise.
One of the assumptions states that agents do not directly observe the conditional mean of consumption growth,  3. Unlike Eraker [5] , we model agents’ inference process about the value of
3. Unlike Eraker [5] , we model agents’ inference process about the value of  from information in both consumption and dividend growth. The inference occurs jointly with the determination of equilibrium prices. The Markov property of the state variables allows the solution of the agent’s optimization problem proceed in two stages. First, we use a linear version (Kalman-Bucy filter) of a general filter to derive the process of an agent’s best estimate of
from information in both consumption and dividend growth. The inference occurs jointly with the determination of equilibrium prices. The Markov property of the state variables allows the solution of the agent’s optimization problem proceed in two stages. First, we use a linear version (Kalman-Bucy filter) of a general filter to derive the process of an agent’s best estimate of ,
,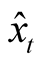 . Second, given the optimal estimate, the model is effectively reduced to a full-information model in which all expectations are computed under an information set available to agents.
. Second, given the optimal estimate, the model is effectively reduced to a full-information model in which all expectations are computed under an information set available to agents.
As a standard practice, we model the optimal forecast of the latent process by minimizing the posterior variance of the latent process4. The following result from Liptser and Shiriaiev [14] summarizes the solution to our optimal filtering problem.
Result (Liptser and Shiriaiev [14] ) Assuming that the latent mean of consumption growth is described by (3) and an agent’s inference is based on the observations of consumption and dividend growth as described in (1) and (2) the agent’s best estimate of ,
, 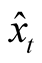 is given by
is given by
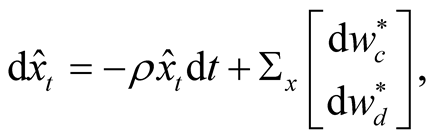 (4)
(4)
where the posterior variance of process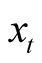 ,
,  , and the instantaneous volatility of the best estimate of
, and the instantaneous volatility of the best estimate of ,
, 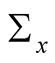 , are given by
, are given by
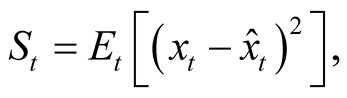 (5)
(5)
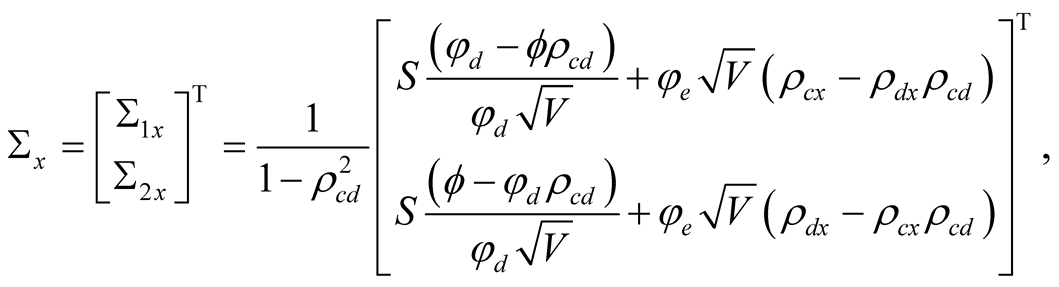 (6)
(6)
Processes  and
and  given by
given by
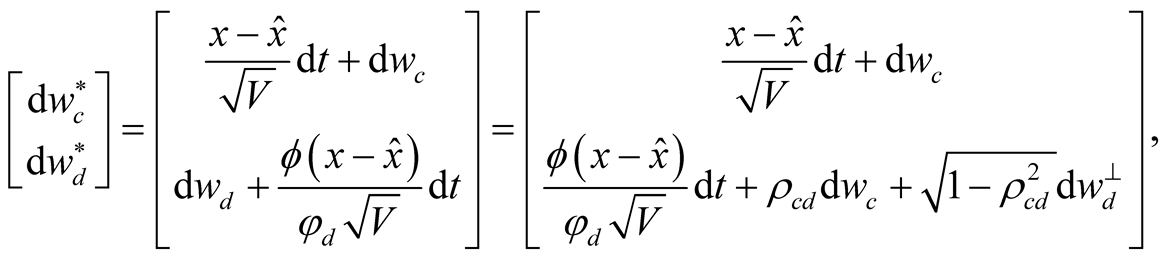 (7)
(7)
are standard Wiener processes under a filtration generated by observation on consumption and dividend growth on the interval , i.e.,
, i.e.,  ,
,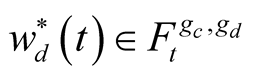 . Here,
. Here,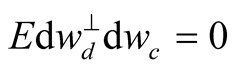 .
.
Posterior variance, 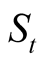 , in Equation (5) is a solution of a deterministic ordinary differential Equation (ODE), which follows from applying Itô’s lemma to the definition of the variance in (5) and taking expectations:
, in Equation (5) is a solution of a deterministic ordinary differential Equation (ODE), which follows from applying Itô’s lemma to the definition of the variance in (5) and taking expectations:
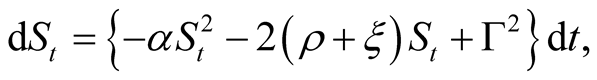 (8)
(8)
where
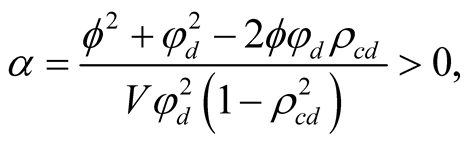

 (9)
(9)
All our subsequent results are given for the steady state case, i.e., . In the steady state posterior variance is given by
. In the steady state posterior variance is given by 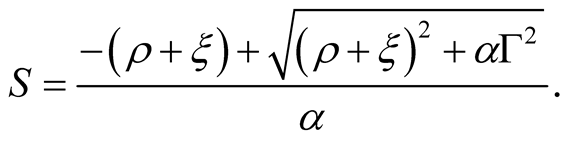
In the general case when correlations of the latent process with consumption and dividend processes are not perfect, each source of information receives a non-zero weight, which is a function of the volatility of that source and its correlation with the latent process .
.
Given the optimal process , processes
, processes  and
and  under the new probability measure corresponding to the information available to agents have the following form:
under the new probability measure corresponding to the information available to agents have the following form:
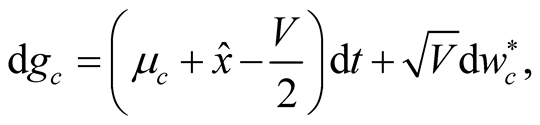 (10)
(10)
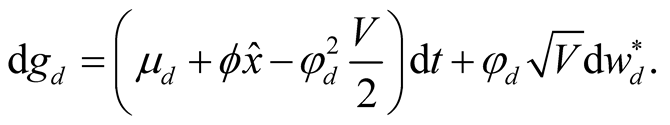 (11)
(11)
We make a further assumption about the preferences of the representative agent in the BY [3] economy.
Assumption 4 We assume a representative agent economy with stochastic differential utility preferences of Duffie and Epstein [20] :
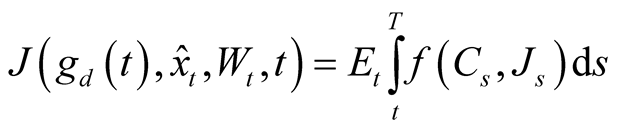 (12)
(12)
with the normalized aggregator,
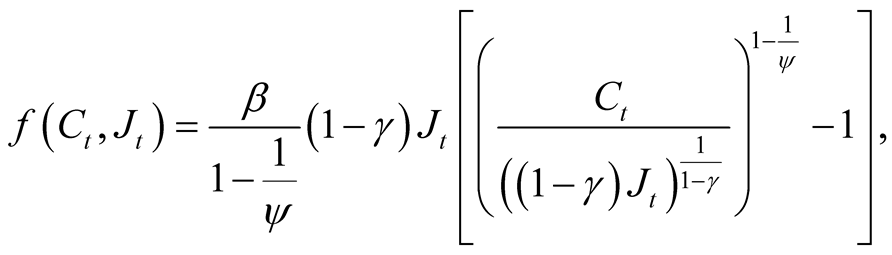 (13)
(13)
where  is the agent’s horizon,
is the agent’s horizon, 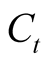 is consumption at time
is consumption at time ,
,  is the recursive utility at time
is the recursive utility at time ,
,  is the subjective discount rate,
is the subjective discount rate,  is the relative risk aversion coefficient, and
is the relative risk aversion coefficient, and 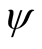 is the elasticity of intertemporal substitution (EIS).
is the elasticity of intertemporal substitution (EIS).
Duffie and Epstein [20] prove the Bellman optimality condition and show that this condition implies that for a given consumption process the optimal differential utility satisfies the following partial differential Equation (PDE)5:
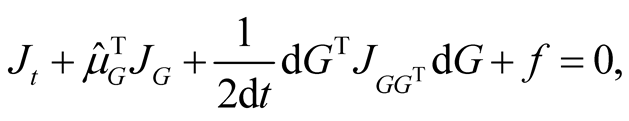 (14)
(14)
 (15)
(15)
where 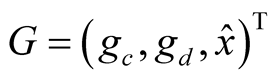 is the
is the 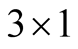 vector of state variables, and
vector of state variables, and 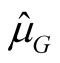 is the mean vector given by
is the mean vector given by
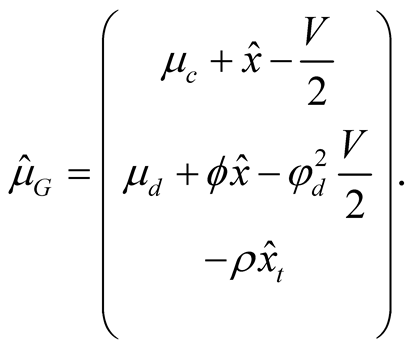
In general, this PDE does not have an analytical solution. To this end, we follow Campbell and Viceira [21] and Zhu [22] and use a log-linear approximation of the normalized aggregator. To arrive at the log-linear approximation we simplify notation by rewriting the aggregator as follows:
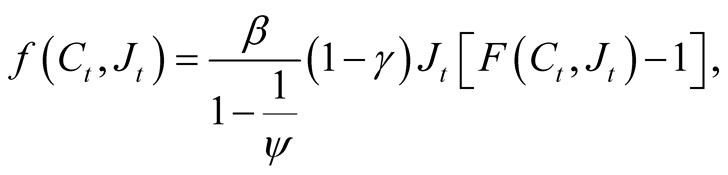
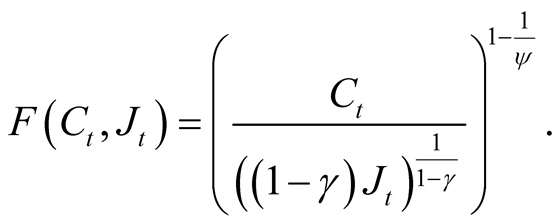
A solution of the Bellman Optimality condition as shown in Campbell and Viceira [21] (page 146) implies that 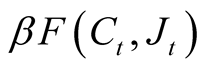 is the optimal consumption-wealth ratio (lower case letters are logs of the actual values):
is the optimal consumption-wealth ratio (lower case letters are logs of the actual values):
 (16)
(16)
A Taylor series expansion around its unconditional mean , produces the desired log-linear approximation, which will remain approximately valid as long as the consumption-wealth ratio is relatively stable:
, produces the desired log-linear approximation, which will remain approximately valid as long as the consumption-wealth ratio is relatively stable:
 (17)
(17)
where
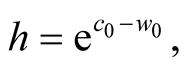 (18)
(18)
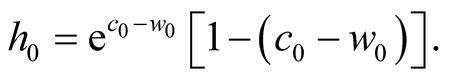 (19)
(19)
Inserting this approximation into the expression of the normalized aggregator in (13), we have:

 (20)
(20)
where
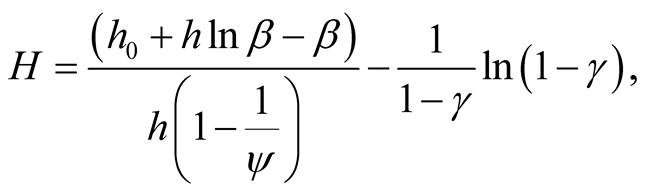
where  is the long-term mean of consumption to wealth ratio.
is the long-term mean of consumption to wealth ratio.
There are two shortcomings of the proposed approximation. The first problem is that the EIS,  , only appears in
, only appears in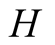 , and has no impact on pricing. To the first order of the log-linearization, EIS does not affect either the aggregator (20) or the value function. Consequently, we cannot analyze its implications for equity prices but the model in this form admits closed-form solutions. Our ultimate goal, however, is to isolate the impact of learning on the dynamics of equity prices.
, and has no impact on pricing. To the first order of the log-linearization, EIS does not affect either the aggregator (20) or the value function. Consequently, we cannot analyze its implications for equity prices but the model in this form admits closed-form solutions. Our ultimate goal, however, is to isolate the impact of learning on the dynamics of equity prices.
Inserting approximation (20) into PDE (14), we look for a solution,  , of the PDE in an exponential-affine form:
, of the PDE in an exponential-affine form:
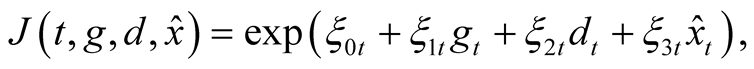 (21)
(21)
where  and
and .
.
Substitution of this function into (14) leads to an affine function of the state variables,  , that must evaluate to zero for arbitrary values of the state variables. This situation is only possible if coefficients the state variables are all zero, which gives rise to a system of four ODEs for coefficients
, that must evaluate to zero for arbitrary values of the state variables. This situation is only possible if coefficients the state variables are all zero, which gives rise to a system of four ODEs for coefficients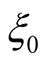 ,
, 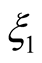 ,
, 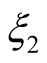 , and
, and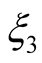 . From this point on we specialize our results to an infinitely lived agent, i.e.,
. From this point on we specialize our results to an infinitely lived agent, i.e., . Subject to appropriate initial condition on the lifetime utility function, the ODEs have the following solutions (see Appendix for details):
. Subject to appropriate initial condition on the lifetime utility function, the ODEs have the following solutions (see Appendix for details):
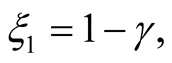 (22)
(22)
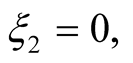 (23)
(23)
 (24)
(24)
The second shortcoming of the proposed log-linearization is evident in (23). Dividend growth does not have a direct effect on either the utility function or the pricing of assets as . The only impact of dividend growth is through its effect on the optimal estimate of the conditional mean of consumption growth due to the nature of agents’ learning process.
. The only impact of dividend growth is through its effect on the optimal estimate of the conditional mean of consumption growth due to the nature of agents’ learning process.
3. Pricing Kernel
Duffie and Epstein [20] show that the stochastic discount factor  is given by the following expression:
is given by the following expression:
 (25)
(25)
Applying Itô’s lemma to (25) (see Appendix for details) and using the expressions for the normalized aggregator approximation in (20) and the state processes in (4), (10), and (11), we obtain the process for the pricing kernel, pt:
 (26)
(26)
where
 (27)
(27)
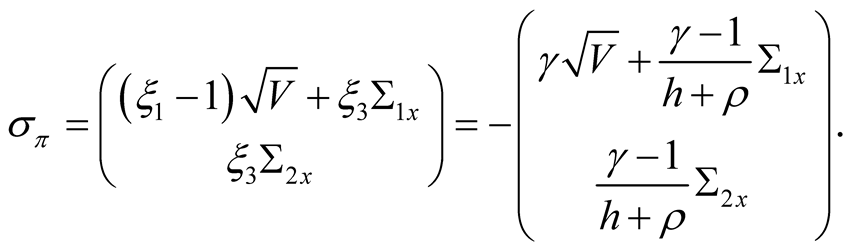 (28)
(28)
Expressions for 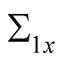 and
and 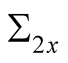 are given in (6). Note that both loadings on consumption and dividend growth shocks in the pricing kernel will generally be negative for agents with
are given in (6). Note that both loadings on consumption and dividend growth shocks in the pricing kernel will generally be negative for agents with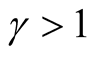 .
.
The real short term risk-free rate,  , is given by the drift in expression (26):
, is given by the drift in expression (26):
 (29)
(29)
It is clear that parameter  plays the role of the central tendency of the resulting mean-reverting short rate process. This interpretation is due to the fact that the estimate of the conditional mean of consumption growth,
plays the role of the central tendency of the resulting mean-reverting short rate process. This interpretation is due to the fact that the estimate of the conditional mean of consumption growth,  , mean reverts to zero (see (4)).
, mean reverts to zero (see (4)).
Equation (29) shows that, the short rate is only a function of time  and the agents’ posterior estimate of the conditional mean of consumption growth,
and the agents’ posterior estimate of the conditional mean of consumption growth,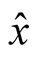 . Itô’s lemma applied to Equation (29) implies that
. Itô’s lemma applied to Equation (29) implies that
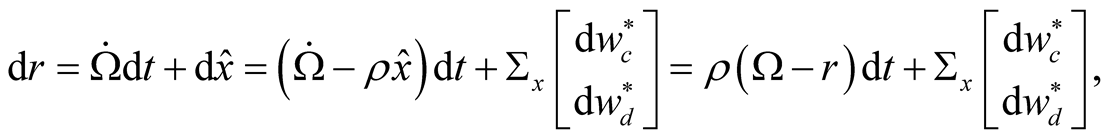 (30)
(30)
where  is the first order time derivative of
is the first order time derivative of  with respect to
with respect to 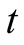 6.
6.
4. Equity Valuation
As an example of equity valuation under our LRR pricing kernel with incomplete information we take the earnings-based stock valuation model of BC [7] . Main ingredients of the model can be summarized as follows. Equity dividends are modeled as, on average, a fraction of the firm’s earnings-per-share (EPS):
 (31)
(31)
where 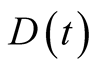 is dividend flow in units of consumption numeraire per unit of time,
is dividend flow in units of consumption numeraire per unit of time,  is earnings per share, and
is earnings per share, and  is white noise uncorrelated with all other Wiener processes.
is white noise uncorrelated with all other Wiener processes.
In practice, many firms do not pay dividends, and the implementation of dividend-based valuation model would be limited. Current specification circumvents this problem by expressing dividends as a fraction of firm’s earnings permitting an earnings-based valuation.
We further assume that earnings growth follows an arithmetic Brownian motion given by
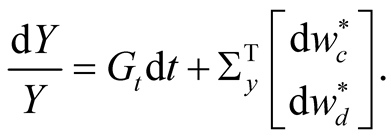 (32)
(32)
The unobserved mean of earnings growth is itself modeled as a Vasiĉek process:
 (33)
(33)
Current version of the model is dynamically complete. This property makes it a little restrictive in that any two traded assets span the entire economy. In principle, we can make the model incomplete by introducing i.i.d. shocks to both processes (32) and (33). Since the shocks would be orthogonal to the pricing kernel in (26), this adjustment would not generate any extra risk premiums and the model would remain largely equivalent to model (32) - (33). Therefore, to save space and avoid parameter proliferation, we keep our complete model version.
It may seem necessary at this point to introduce another filtering problem to model how investors learn about the unobserved mean of earnings growth. However, it is not so. Due to a two-factor nature of the economy in our model, we can solve for 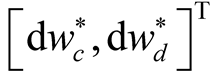 from Equations (10) - (11). As a result, the vector of shocks driving the economy is simply a deterministic function of the two observed state variables
from Equations (10) - (11). As a result, the vector of shocks driving the economy is simply a deterministic function of the two observed state variables 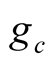 and
and  and the posterior estimate of the conditional consumption mean,
and the posterior estimate of the conditional consumption mean, . The latter is itself a function of the two observed state variables as evident from (4).
. The latter is itself a function of the two observed state variables as evident from (4).
Following the BC [7] model we consider a continuous-time, infinite-horizon economy. Unlike in the BC [7] model, pricing kernel in our model is not exogenously specified, rather it is the endogenous result of agent optimization problem (see Equation (26)). From fundamental valuation principles, the share price of a firm’s equity is the sum of expected present value of all future dividends:
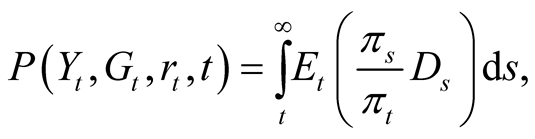
where 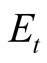 is the time-
is the time-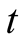 conditional expectation operator with respect to the objective probability measure under a filtration generated by observation on consumption and dividend growth on the interval
conditional expectation operator with respect to the objective probability measure under a filtration generated by observation on consumption and dividend growth on the interval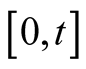 , i.e.,
, i.e.,  ,
,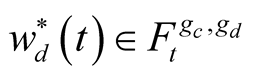 .
.
Based on the above discussion, the equilibrium stock price at time t can be expressed as a function of three state variables: Yt, Gt, and rt, where the latter is the endogenous short rate process in (29). The inference about 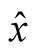 in our model affects risk premium and equilibrium prices reflecting investors’ uncertainty about estimates of
in our model affects risk premium and equilibrium prices reflecting investors’ uncertainty about estimates of .
.
The stock price must satisfy the following PDE with the pricing kernel given in (26):
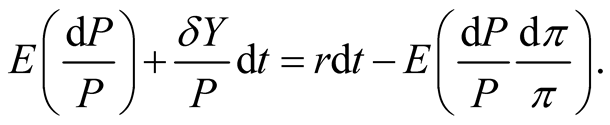 (34)
(34)
We look for a time- stock price solution in the following form:
stock price solution in the following form:
 (35)
(35)
where  represents average dividend-per-share and
represents average dividend-per-share and  is the time-
is the time- price-dividend ratio.
price-dividend ratio.
In our case, the PDE for the stock price takes the following form (see Appendix for derivation):
 (36)
(36)
where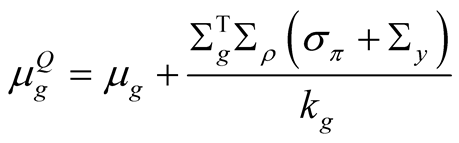 ,
, 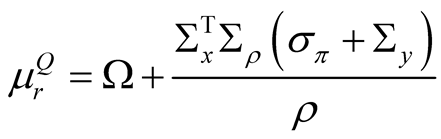 ,
,  is the instantaneous volatility of the pricing kernel given in (28),
is the instantaneous volatility of the pricing kernel given in (28),  is the instantaneous volatility of the estimated latent state process (see (6)), and
is the instantaneous volatility of the estimated latent state process (see (6)), and
 .
.
Given the affine nature of the short rate process, Equations (26), (29), and (34) imply that the solution for the stock price has an exponential-affine form as a function of posterior mean of conditional consumption growth,  (see Appendix for further details). Since
(see Appendix for further details). Since  is affine (see (29)) in the short rate,
is affine (see (29)) in the short rate,  , then stock price itself is an affine function of the short rate.
, then stock price itself is an affine function of the short rate.
Theorem 1 The real price of a stock paying an infinite stream of dividends as specified in (31) is given by an integral of an exponential-affine function of the state variables:
 (37)
(37)
where functions ,
, 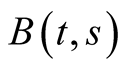 and
and 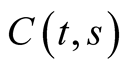 are given by
are given by
 (38)
(38)
 (39)
(39)
 (40)
(40)
The real equity risk premium is defined by the negative covariance of the pricing kernel and equity return and has the following form:
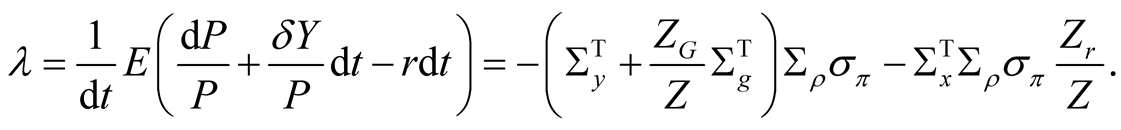 (41)
(41)
The transversality condition,  , that prohibits price bubbles has the following form:
, that prohibits price bubbles has the following form:
 (42)
(42)
Proof: See Appendix.
We can write the expression for the instantaneous equity risk premium in (41) as the sum of three components:
 (43)
(43)
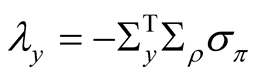 (44)
(44)
 (45)
(45)
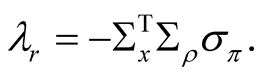 (46)
(46)
Note that in (26) - (28) the weights on consumption and dividend growth, 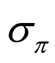 , in the pricing kernel are negative for investors with risk aversion coefficient
, in the pricing kernel are negative for investors with risk aversion coefficient . Therefore, generally, all three risk premiums-
. Therefore, generally, all three risk premiums-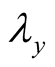 ,
,  , and
, and  -are expected to be positive7.
-are expected to be positive7.
The result is similar to that in BC [7] , BC [23] , and JPW [6] . The premium is a weighted sum of risks associated with shocks to earnings growth, its mean, and the short rate8. The weights are the elasticities (log-derivatives) of the equity price to these state variables.
Our approach is, however, different from that in the above papers because the pricing kernel in our model is endogenously determined in equilibrium. As a result, prices of risk for the shocks to the three state variables in our model are all endogenous unlike those in BC [7] , BC [23] , and JPW [6] , who need to estimate them directly from the data. In our model, we obtain the prices of risk indirectly by estimating the parameters of more fundamental state processes such as aggregate consumption and dividend growth along with latent conditional consumption mean. In addition, the contribution of the variation of the short rate is not affected by learning at all in BC [7] , BC [23] , and JPW [6] . In our model, however, due to pricing kernel being directly affected by learning in equilibrium, uncertainty about unobserved conditional mean of consumption growth affects the contribution of the short rate to the equity premium as well. These extra explicit model restrictions on the prices of risk make our modeling approach more parsimonious and potentially less subject to overfitting.
In the remainder of this section we present the details of our calibration exercise and the computation of the equity premium in our model. For reference, our parameter vector consists of 18 components:
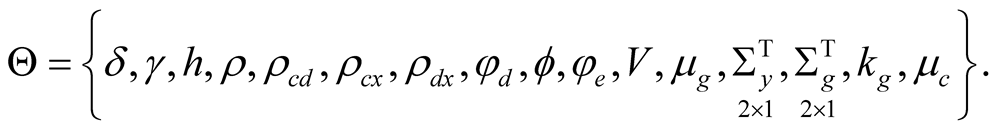
To start, we calibrate parameters of fundamental processes—consumption growth, its mean, and dividend growth. There are 11 parameters included in this set: ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 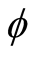 ,
, 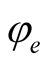 ,
,  , and
, and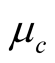 . We choose to adopt the estimates of Constantinides and Ghosh [24] (CG hereafter). They use the Generalized Method of Moments (GMM) to estimate the version of BY [3] model with random volatility of consumption growth and its mean9. Recall that parameter
. We choose to adopt the estimates of Constantinides and Ghosh [24] (CG hereafter). They use the Generalized Method of Moments (GMM) to estimate the version of BY [3] model with random volatility of consumption growth and its mean9. Recall that parameter  is the sample average of consumption-wealth ratio. Lustig, Van Nieuwerburgh, and Verdelhan’s [25] estimate of the log wealth-consumption ratio is 5.86 from the data (and closely matched by its estimate from the LRR model). We set parameter
is the sample average of consumption-wealth ratio. Lustig, Van Nieuwerburgh, and Verdelhan’s [25] estimate of the log wealth-consumption ratio is 5.86 from the data (and closely matched by its estimate from the LRR model). We set parameter 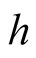 equal to
equal to 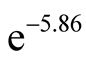 for our calibration exercise. Since our results, specifically equity premium, are very sensitive to the value of the persistence parameter
for our calibration exercise. Since our results, specifically equity premium, are very sensitive to the value of the persistence parameter , we will calibrate it to the observed equity premium and see if its calibrated values are reasonably consistent with observations.
, we will calibrate it to the observed equity premium and see if its calibrated values are reasonably consistent with observations.
Following CG [24] , for our base case we assume that consumption and dividend shocks are uncorrelated with conditional consumption mean,  , i.e.,
, i.e.,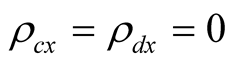 . However, we set the correlation between consumption and dividend growth shocks equal to its sample estimate,
. However, we set the correlation between consumption and dividend growth shocks equal to its sample estimate,  10. Also, we take the relative risk aversion to be equal to 10 as reported by CG [24] 11. Note that parameters
10. Also, we take the relative risk aversion to be equal to 10 as reported by CG [24] 11. Note that parameters  and
and 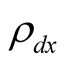 play important role in our model. They measure how fast and how precisely agents can learn about the unobserved mean of consumption growth,
play important role in our model. They measure how fast and how precisely agents can learn about the unobserved mean of consumption growth, . Taking their values equal to zero is tantamount to assuming an environment in which learning is difficult. More exactly, increasing the absolute values of these correlations would improve learning by reducing posterior variance of the filtered estimate,
. Taking their values equal to zero is tantamount to assuming an environment in which learning is difficult. More exactly, increasing the absolute values of these correlations would improve learning by reducing posterior variance of the filtered estimate,  (see Equation (8)). In the extreme case of perfect correlations (either positive or negative), perfect learning obtains as the steady-state posterior variance is zero12. Later, we provide an example of how results change if we increase these correlations.
(see Equation (8)). In the extreme case of perfect correlations (either positive or negative), perfect learning obtains as the steady-state posterior variance is zero12. Later, we provide an example of how results change if we increase these correlations.
We set mean annual consumption growth to 1.9% per year as CG [24] . Leverage parameter,  , and parameters governing conditional volatilities of consumption and dividend growth,
, and parameters governing conditional volatilities of consumption and dividend growth, 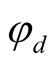 and
and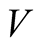 , are matched with the corresponding values estimated in CG [24] :
, are matched with the corresponding values estimated in CG [24] :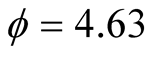 ,
, 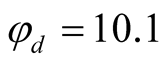 , and
, and . Further, we calibrate latent state variance parameter,
. Further, we calibrate latent state variance parameter,  , by matching the unconditional volatilities of the conditional consumption mean,
, by matching the unconditional volatilities of the conditional consumption mean, 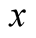 , in CG [24] to that in our model. In doing so, we assume for simplicity that the conditional volatility of consumption (economic uncertainty in LRR model) in CG [24] is constant and equal its estimated value. In this case, discrete LRR model in CG [24] implies that given the state Equation:
, in CG [24] to that in our model. In doing so, we assume for simplicity that the conditional volatility of consumption (economic uncertainty in LRR model) in CG [24] is constant and equal its estimated value. In this case, discrete LRR model in CG [24] implies that given the state Equation:
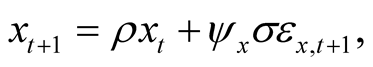
the unconditional variance of 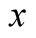 takes the following form:
takes the following form: , where a time-series persistence parameter
, where a time-series persistence parameter  and
and 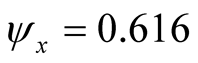 (both from Table 6 of CG [24] ). Our model (3), once exactly dicretized, implies that the steady-state variance of
(both from Table 6 of CG [24] ). Our model (3), once exactly dicretized, implies that the steady-state variance of 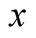 is
is . Equating the two results we have the following expression for the calibrated value of our parameter
. Equating the two results we have the following expression for the calibrated value of our parameter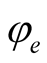 :
: .
.
The second parameter group is related to the earnings growth process (32)-(33). This group includes seven parameters: ,
, 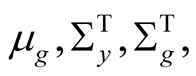 and
and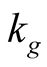 .
.
Monthly dividend and EPS data come from COMPUSTAT for S&P500 and cover the period from 1982 January to 2013 September. Based on these data, we estimate historical dividend-payout-ratio, 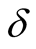 , to be equal to 0.37.
, to be equal to 0.37.
We follow BC [7] , BC [23] , and JPW [6] and use current year analyst forecast of earnings growth from I/B/E/S (monthly FY1 earnings-per-share data) as a proxy for earnings growth. To obtain parameter values for the earnings growth process (32) - (33), we run a Kalman filter on the system (32) - (33) rewritten as follows:
 (47)
(47)
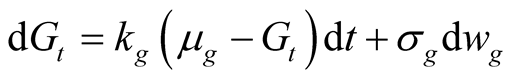 (48)
(48)
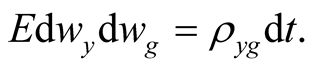 (49)
(49)
Annualized Kalman filter estimates for long-term mean of earnings growth,  , and the speed of mean reversion,
, and the speed of mean reversion, 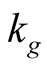 , are 8.13% and 5.9, respectively13. In computing price-earnings ratio in (37), we set G equal to its sample mean of 8.23% and
, are 8.13% and 5.9, respectively13. In computing price-earnings ratio in (37), we set G equal to its sample mean of 8.23% and  to its unconditional mean
to its unconditional mean . Further, given our Kalman filter estimates for
. Further, given our Kalman filter estimates for ,
,  ,
, 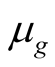 , and
, and 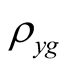 we can now back out our earnings growth parameters
we can now back out our earnings growth parameters 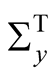 and
and  by matching the corresponding second moments of the two state variables as follows (numerical values are Kalman filter estimates)14:
by matching the corresponding second moments of the two state variables as follows (numerical values are Kalman filter estimates)14:
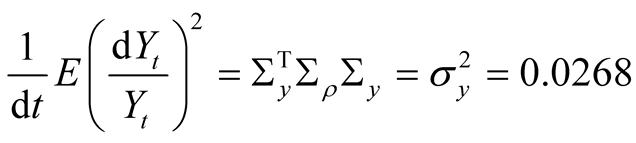
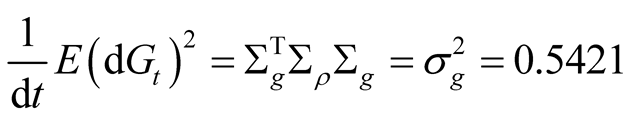
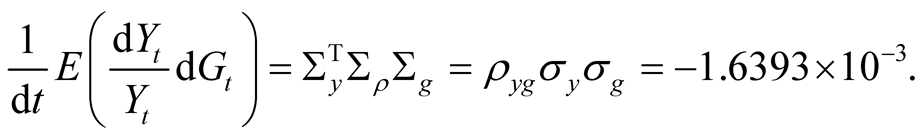
We start our equity risk premium exercise from the base case, i.e., we set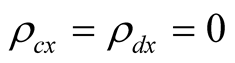 . Our calibrated value of
. Our calibrated value of  for the base case is 0.02415. At this value the real risk premium,
for the base case is 0.02415. At this value the real risk premium,  , in (41) is equal to 5.86%. Given that inflation over the post-war period has averaged about 3.6%, the nominal risk premium implied by our model is about 9.46%. Interestingly, this estimate is a little higher than the values we see in the data. E.g., for the time period from January 1982 to September 2013 the monthly equity premium is 73 bp on average, which amounts to 8.76% per year. We have to keep in mind, however, that this result is likely affected by the fact that key learning parameters are set to zero at this point. Another interesting result is related to the composition of the premium. The components of the real risk premium as specified in Equation (43) have the following values:
, in (41) is equal to 5.86%. Given that inflation over the post-war period has averaged about 3.6%, the nominal risk premium implied by our model is about 9.46%. Interestingly, this estimate is a little higher than the values we see in the data. E.g., for the time period from January 1982 to September 2013 the monthly equity premium is 73 bp on average, which amounts to 8.76% per year. We have to keep in mind, however, that this result is likely affected by the fact that key learning parameters are set to zero at this point. Another interesting result is related to the composition of the premium. The components of the real risk premium as specified in Equation (43) have the following values:
 ,
, 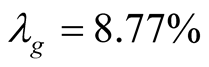 ,
,  ,
, 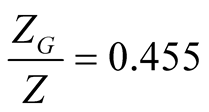 , and
, and .
.
First, there is a striking difference in the value of  in our model compared to that in BC [23] and JPW [6] . In our case, the premium on the mean earnings growth is similar in magnitude to the premium due to shocks in earnings growth itself. In the above papers, however, mean earnings growth has largely trivial magnitude. Second, only about 45% of the mean earnings growth premium contributes to the overall equity premium
in our model compared to that in BC [23] and JPW [6] . In our case, the premium on the mean earnings growth is similar in magnitude to the premium due to shocks in earnings growth itself. In the above papers, however, mean earnings growth has largely trivial magnitude. Second, only about 45% of the mean earnings growth premium contributes to the overall equity premium
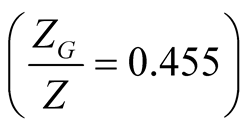 , which makes earnings growth the most important contributor to the equity premium. Finallyeven though short rate risk premium is small
, which makes earnings growth the most important contributor to the equity premium. Finallyeven though short rate risk premium is small 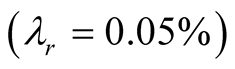 16, it is positive. Combined with the fact that the elasticity of the price to the short rate is negative and very high in absolute value, the short rate contribution amounts to a reduction in the equity premium of about 5% and largely offsets the risk premium component due to mean earnings growth,
16, it is positive. Combined with the fact that the elasticity of the price to the short rate is negative and very high in absolute value, the short rate contribution amounts to a reduction in the equity premium of about 5% and largely offsets the risk premium component due to mean earnings growth, . We also note that as we reduce the value of parameter
. We also note that as we reduce the value of parameter , the risk premium increases and the price earnings (P/E) ratio declines.
, the risk premium increases and the price earnings (P/E) ratio declines.
Next we present equity premium results for several values of the learning parameters 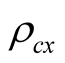 and
and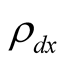 . We set parameter
. We set parameter  to avoid violation of constraint (42) at new values of
to avoid violation of constraint (42) at new values of 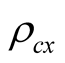 and
and . Now we increase the values of parameters
. Now we increase the values of parameters 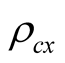 and
and  from 0.1 to 0.3. When
from 0.1 to 0.3. When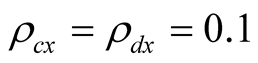 , the real risk premium is 5.23%, which implies the nominal risk premium of 8.83%, in line with historical average. At the same time, the model P/E ratio is 23.63 and the nominal risk free rate is 5.49%. For comparison, in our sample the average P/E is 18.25 ranging from 9.6 to 45.6, and the 3-month nominal interest rate is 5.15% on average varying from 0.03% to 13.48%. Thus, for these correlation values the risk premium, P/E ratio, and the risk free rate match well to corresponding values in the data. As we increase the correlations, risk premium declines and P/E ratio increases. E.g., for
, the real risk premium is 5.23%, which implies the nominal risk premium of 8.83%, in line with historical average. At the same time, the model P/E ratio is 23.63 and the nominal risk free rate is 5.49%. For comparison, in our sample the average P/E is 18.25 ranging from 9.6 to 45.6, and the 3-month nominal interest rate is 5.15% on average varying from 0.03% to 13.48%. Thus, for these correlation values the risk premium, P/E ratio, and the risk free rate match well to corresponding values in the data. As we increase the correlations, risk premium declines and P/E ratio increases. E.g., for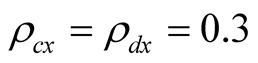 , nominal equity risk premium is 6.74%, P/E ratio is 18.72, and nominal risk free rate is 5.44%. It appears that the model is capable of matching risk premium, P/E ratio, and risk free rate to the values observed in the data. However, we notice that the relation between P/E ratio and the instantaneous risk premium is non-monotonic. Our results suggest that for relatively small
, nominal equity risk premium is 6.74%, P/E ratio is 18.72, and nominal risk free rate is 5.44%. It appears that the model is capable of matching risk premium, P/E ratio, and risk free rate to the values observed in the data. However, we notice that the relation between P/E ratio and the instantaneous risk premium is non-monotonic. Our results suggest that for relatively small  higher risk premium implies smaller P/E ratios. However, when
higher risk premium implies smaller P/E ratios. However, when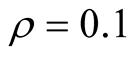 , the relation is positive in that higher values
, the relation is positive in that higher values 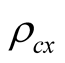 and
and  lead to lower risk premium and also lower P/E ratios.
lead to lower risk premium and also lower P/E ratios.
We have applied the model only to match several data moments such as average P/E ratio of an index portfolio, equity risk premium, and nominal interest rate. It remains to be seen how well the model will work in cross-section when applied to several assets such as, e.g., size, book-to market, and momentum portfolios.
5. Conclusions
We derive a model of equity valuation in an economic environment in which low frequency trends in state variables (long-run risks) play a crucial role in asset valuation. We extend the LRR model of BY [3] to include learning about the latent conditional mean of consumption growth. We explicitly model how investors learn about the latent variable. We show that there are closed form solutions for equity prices and the instantaneous equity premium under this new risk-neutral measure.
We derive an equilibrium pricing kernel that contains all information about learning. As a result, in our model unlike in previous literature, due to the pricing kernel being affected by learning in equilibrium, uncertainty about unobserved conditional mean of consumption growth affects all contributions to the equity premium, those from shocks to earnings growth, its mean, and the short rate.
Further, in contrast to previous work in this line of literature, in our model, short rate is determined endogenously from the drift of the stochastic discount factor. One of the model’s implications is that the short rate is an affine function of the estimated conditional mean of consumption growth and, thus, inherits its mean-reverting property. One of the interesting aspects of the endogeneity of the short rate is its negative contribution to the overall equity premium.
We calibrate the model to aggregate dividends and consumption and CRSP index earnings process. The model can reproduce the levels of CRSP index price-earnings ratios, equity risk premium, and the short maturity interest rate. Further work would require full estimation of the model. We leave cross-sectional and time-series tests of the model for future work.
Appendix
A.1. Derivation of the Value Function, J.
Once we substitute the log-linear approximation (20) into the PDE (14), it becomes a parabolic PDE with coefficients affine in state variables. It is natural to look for a solution, 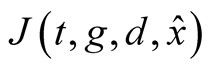 , of (14) in an exponential affine form:
, of (14) in an exponential affine form:
 (50)
(50)
Upon the substitution of (50) into (14) the PDE becomes an identity that must hold for arbitrary values of state variables (symbol  denotes the partial derivative with respect to the time variable,
denotes the partial derivative with respect to the time variable,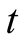 ):
):
 (51)
(51)
where the expressions for the mean of the state vector,  , and the aggregator,
, and the aggregator,  , immediately follow from (14), (20), and (50):
, immediately follow from (14), (20), and (50):
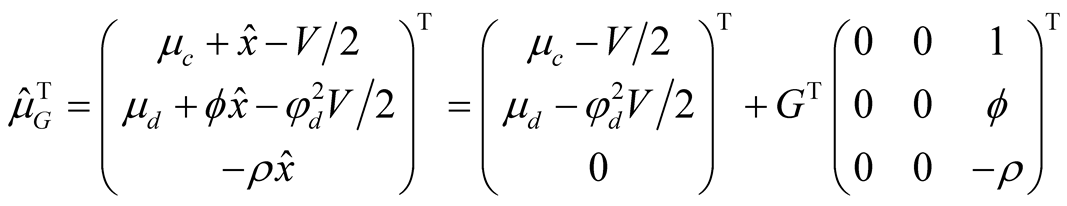
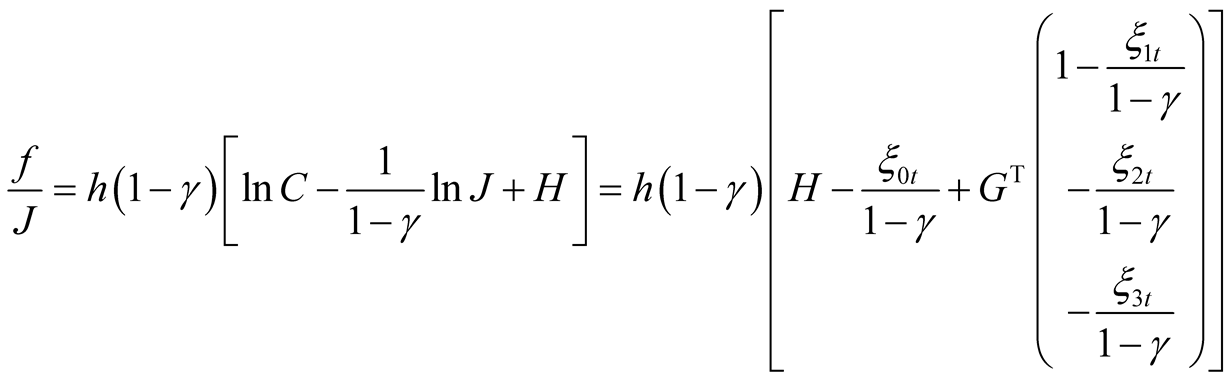
Because identity (51) must hold for all values of state variables, coefficients on the state variables must all be zero. Since  does not affect any further results, we do not attempt to solve for
does not affect any further results, we do not attempt to solve for 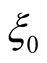 and ignore it in our further discussions.
and ignore it in our further discussions.
Collecting terms containing the state variable vector we find that
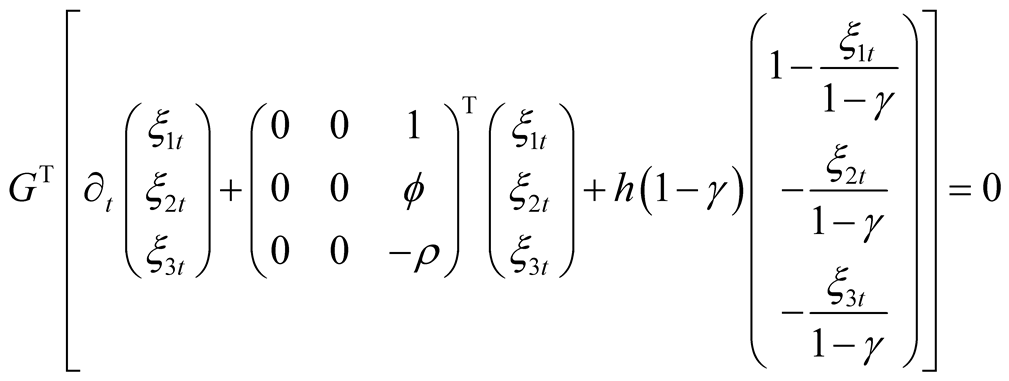
The above identity holds if and only if the following conditions are satisfied:
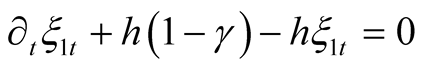 (52)
(52)
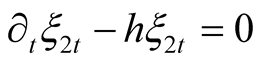
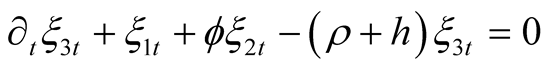
subject to terminal condition (15), i.e.,

This is a system of joint ODEs for coefficients ,
, 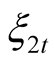 , and
, and .
.
Solving the system for an infinitely lived agent , we finally have
, we finally have
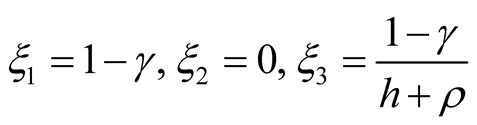
A.2. Derivation of the Pricing Kernel in (26)
The normalized Porteus-Kreps aggregator has the following approximate form:
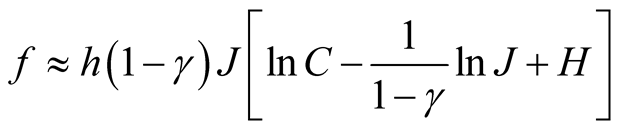
Duffie and Epstein [26] show that the SDF can be expressed in terms of the aggregator as in (25). Applying Itô’s lemma to (25) we have
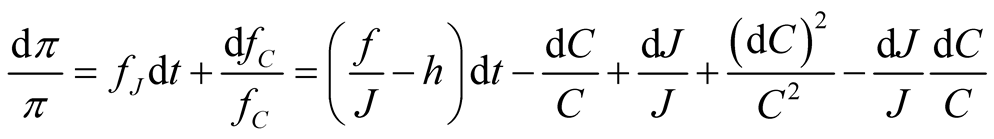 (53)
(53)
Recall that the value function,  , and the consumption process,
, and the consumption process,  , obey the following SDEs:
, obey the following SDEs:
 (54)
(54)
 (55)
(55)
Also, from (21) we have
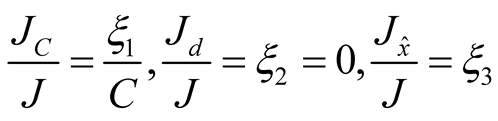
Combining the above results we have the following expression for the pricing kernel:
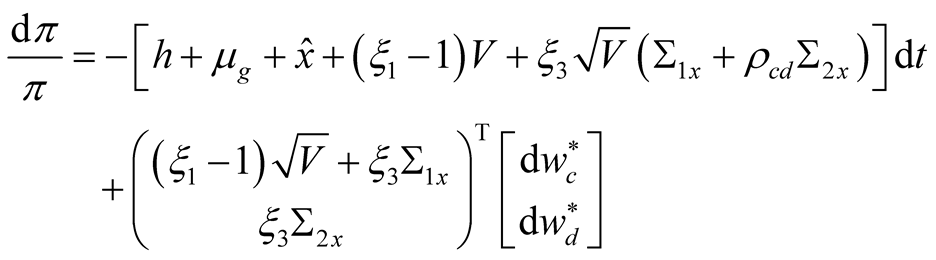
where 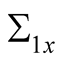 and
and 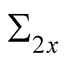 are the two components of
are the two components of 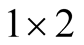 vector
vector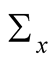 .
.
A.3. Derivation of the Stock Price, 𝑷𝒕
We derive the share price using standard SDE arguments based on a stochastic discount factor (SDF) approach (see, e.g., Cochrane [2] ).
With the pricing kernel given in (26), the stock price must satisfy the following PDE:
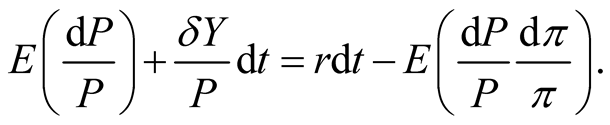 (56)
(56)
We look for a time- stock price solution in the following form:
stock price solution in the following form:
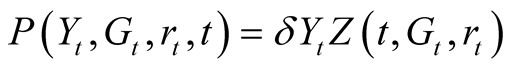
where  represents average dividend-per-share and
represents average dividend-per-share and  is the time-
is the time- price-dividend ratio. Applying Itô’s rule to
price-dividend ratio. Applying Itô’s rule to :
:
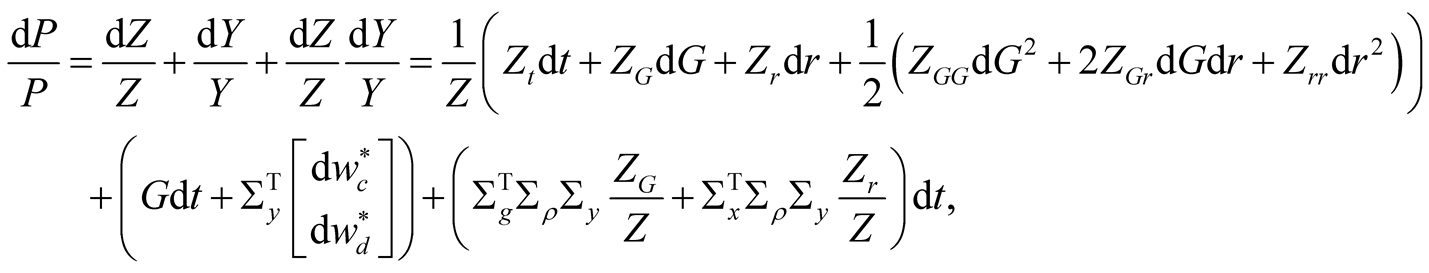 (57)
(57)
 (58)
(58)
Collecting all the terms in (56), taking the expectation, and dividing throughout by dt, we obtain the PDE for the share price:
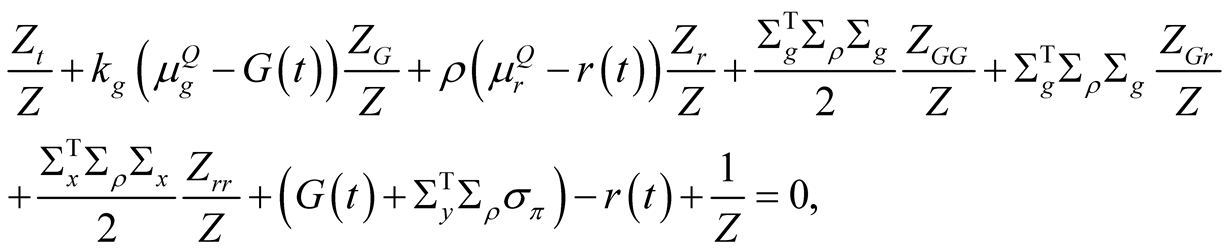 (59)
(59)
where .
.
We seek a price-dividend ratio in the form:
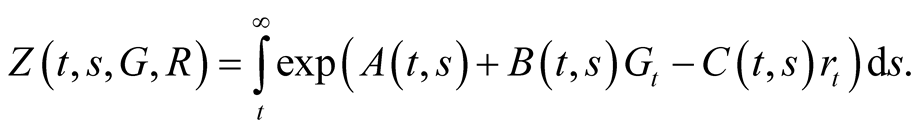 (60)
(60)
Inserting this conjecture into (59) and recognizing that the resulting ordinary differential Equation (ODE) must hold for arbitrary values of G(t) and r(t), we get the following ODEs for functions A(t, s), B(t, s), and C(t, s):
 (61)
(61)
with the initial conditions 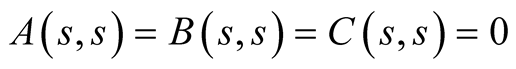
Subject to these initial conditions, the solution of the system (61) is:
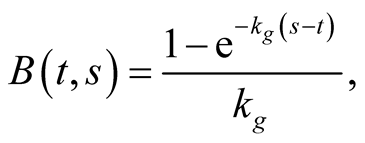
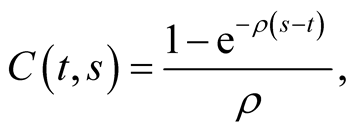
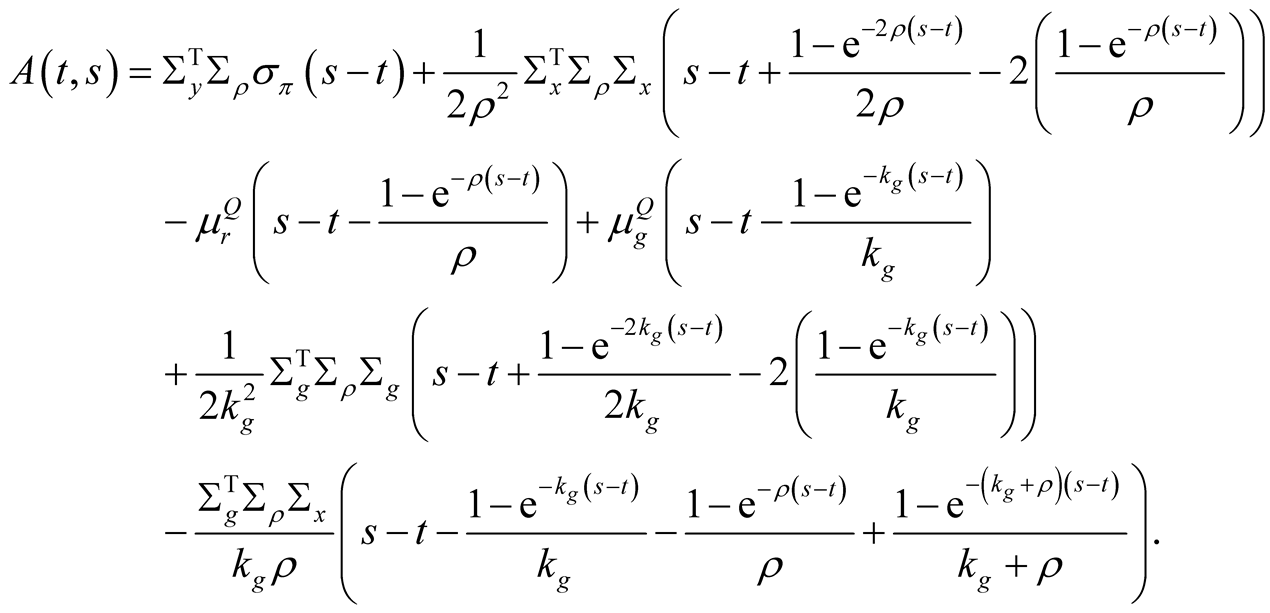
For the integral (60) to exist, the integrand should be declining with s sufficiently fast. Since  and
and  are bounded, function
are bounded, function  should be negative and unbounded at large
should be negative and unbounded at large  which implies a transversality condition on the model parameters. To derive the transversality condition, we notice that any term containing an expression of the form
which implies a transversality condition on the model parameters. To derive the transversality condition, we notice that any term containing an expression of the form  with a positive
with a positive  is bounded. After ignoring all bounded and collecting all unbounded terms, we have
is bounded. After ignoring all bounded and collecting all unbounded terms, we have

where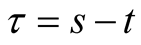 . The transversality condition requires that the leading terms must be negative for the price integral to exist:
. The transversality condition requires that the leading terms must be negative for the price integral to exist:
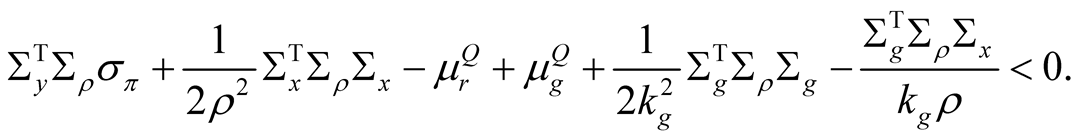
Equation (58) implies that the instantaneous equity risk premium is
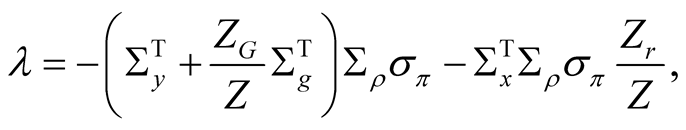
which has three components: 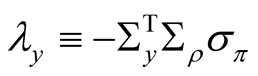 is the risk premium due to earnings growth shocks,
is the risk premium due to earnings growth shocks,
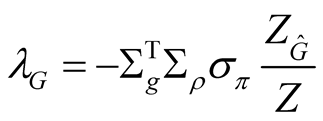 is the risk premium due to shocks to the mean of earnings growth, and
is the risk premium due to shocks to the mean of earnings growth, and 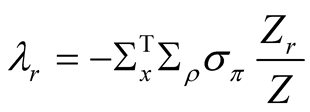
NOTES
1A number of other studies explore incomplete information about an unobservable state variable, such as the dividend growth rate, with respect to asset valuation (see, Timmermann ; Brennan ; Veronesi ; Brennan and Xia ; and Lewellen, and Shanken ).
2Since equity valuation model in BC is not applicable to stocks with zero or negative earnings, Dong and Hirshleifer propose a refinement of earnings process in the BC model. However, both models implicitly assume that the latent state variable is observed and ignore the estimation risk premium resulting from investors’ learning process.

3Eraker extends BY’s economy to general affine state variable processes. However, both Eraker and BY assume that the conditional mean of consumption growth,  , is observable.
, is observable.
4Estimation risk resulting from some state variables being unobservable from market data is recognized in studies that examine the role of learning in incomplete information environments (see, for example, Williams ; Dothan and Feldman ; Detemple ; Gennotte ; Timmermann ; Brennan ; and Feldman ).

5Boundary condition (15), in principle, causes technical difficulties (see Duffie and Epstein ). Following Duffie and Epstein we modify the condition to . This change has no impact on any pricing implications in our model.
. This change has no impact on any pricing implications in our model.

6In the steady state, for an infinitely lived agent 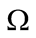 is constant.
is constant.

7Both components of the posterior variance of the conditional consumption mean,  , are positive in our calibration exercise.
, are positive in our calibration exercise.
8JPW extend BC by modeling the posterior estimate (by representative agents) of shocks to the unobserved mean of earnings growth. Shocks to earnings growth are the only source of information in agents’ learning exercise. As a result, the equity premium comes from risks due to variation in earnings growth and from that in the short rate, with the earnings component of risk premium corrected for the extra uncertainty due to sampling variation in the posterior estimate of the mean of earnings growth.

9CG argue that the latent state variables of BY model—the conditional mean of the aggregate consumption growth rate and the conditional variance of its innovation—are hard to measure in the data. Since BY model imposes deterministic restrictions on the state variables, CG express the two state variables as known affine functions of the observable aggregate log price/dividend ratio and log risk-free rate, essentially treating them as observables as well.
10Consumption data series comes from BEA (personal consumption expenditure: nondurable goods and services, PCE implicit price deflator, and the CPI for all urban consumers). All items are quarterly and range from 1947: 1 to 2013: 4. One issue in constructing the consumption growth series is that the data on real personal consumption expenditure (PCE) on non-durables plus services are not reported. According to BEA’s explanation on how to form the real data series, the consumption excluding durables cannot be retrieved by simply adding real consumption on non-durables and that on services together. Instead, we compute the required consumption expenditure by adding nominal PCE on non-durables and that on services, and then deflating the sum using the corresponding price deflator. However, the implicit price deflator on our constructed PCE series is not reported. Instead, we use the price deflator on total PCE and the CPI for all urban consumers as two proxies when deflating the consumption series and computing the inflation. We compute nominal dividend growth from monthly CRSP Stock Market Indexes using both value-weighted returns with and without distributions. To obtain quarterly real dividend growth, we convert monthly dividend growth rate to quarterly rate by compounding three monthly rates within each quarter and deflating the quarterly rate using inflation rates based on PCE price deflator.
11All CG parameters that we adopt in our calibration are from their Table 6, in which they estimate BY LRR model on six assets over a post-war period 1947-2009.
12If either  or
or 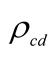 is equal to +1 or −1, Equation (9) implies that
is equal to +1 or −1, Equation (9) implies that 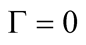 and the steady-state posterior variance of
and the steady-state posterior variance of 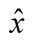 is also zero.
is also zero.

13Given that  is estimated to be 0.5421, the value of 5.9 for
is estimated to be 0.5421, the value of 5.9 for 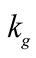 implies the steady state standard deviation of earnings growth mean,
implies the steady state standard deviation of earnings growth mean, 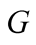 , of 21.4%.
, of 21.4%.
14This system gives us three equations in four unknowns. We chose to set earnings growth loading on consumption shocks, 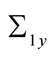 , to 0.13 to minimize the likelihood of violating the transversality condition (42).
, to 0.13 to minimize the likelihood of violating the transversality condition (42).
15Note that  in our model corresponds to
in our model corresponds to  in the discrete version of CG .
in the discrete version of CG .
16It is four times smaller in magnitude that that in BY .