1. Introduction
It is well-known that, plasma is a hot ionized gas consisting of approximately equal numbers of positively charged ions and negatively charged electrons. The characteristics of plasmas are significantly different from those of ordinary neutral gases so that plasmas are considered a distinct fourth state of matter. There are numerous everyday uses for plasmas, for example, fluorescent lights and neon signs work because of plasma. Circuit features on micro-processor chips in computers also contain plasma. Even the exhaust that is emitted during rocket launches is actually plasma, not gas. Plasma is also used to manufacture industrial diamonds and superconducting films. Plasma is also a key technology in the development of alternative energy sources. Nuclear fusion, which is plasma based, is one of the most promising candidates for the energy needs of the future when fossil fuels finally run out. One of the important models rises in hydrodynamic plasma called the RayleighTaylor instability (RTI) problem [1] [2] . RTI can occur when dense plasma is supported against the gravity. Studies on RTI show that this instability is troublesome because it obstructs the realization of ICF [3] [4] . In astrophysics, this instability is related to the stellar structure and evolution [5] [6] . Hence, it is important to understand the physical mechanisms that can affect such instability, especially its suppression as well as the details of this instability. Such knowledge will aid our understanding of the origin of white dwarfs and type-Ia supernovas.
Also, it is well-known that, the plasmas are strongly influenced by magnetic fields (where the plasma parameters may vary with the application of magnetic field), where the behavior of plasmas in the presence of a magnetic field is among the oldest problems in plasma physics. It has been central in plasma fusion research since the early experiments on plasma confinement by a magnetic field in the 1950s, and it has remained great interest in plasma fusion studies that use contemporary sophisticated devices [7] . It is also an important problem for many plasma discharges used in processing semiconductor materials where the application of a magnetic field results in enhancement of some desirable features of specific plasma sources [8] . The linear growth rate of RTI has been obtained by Goldston and Rutherford [9] under fixed boundary conditions. The hydromagnetic stability of a magnetized plasma of variable density is of considerable importance in several astrophysical situations, e.g. in theories of sunspot magnetic fields, heating of solar corona and the stability of stellar atmospheres in magnetic fields. Ariel [10] investigated the stability of an inviscid compressible fluid of variable density in the presence of a uniform vertical magnetic field and viscous plasma has been investigated by Bhatia [11] . The instability of stratified plasmas in the presence of horizontal magnetic field of compressible plasmas is studied by Bhimsen [12] . The RTI of a plasma layer in the presence of a horizontal magnetic field is investigated, taking into account the effects of Hall-currents and an arbitrarily large density gradient by Ariel [13] . The effects of horizontal magnetic field, Hall currents and viscosity have been studied on the RTI of an incompressible infinitely conducting stratified plasma by Ahsan and Bhatia [14] . The effect of horizontal magnetic field of Hall currents have been investigated on the RTI of a finitely conducting stratified partially ionized plasma by Aiyub and Bhatia [15] . The instability of stratified plasmas in the presence of horizontal magnetic field of incompressible plasmas with the effect of a transverse velocity shear was studied by Wu et al. [16] . The effect horizontal magnetic field on RTI of a plasma layer in the presence of quantum mechanism was studied by Jintao et al. [17] . The effects of vertical magnetic field in the presence of quantum mechanism on RTI inviscous and viscous plasma were studied by Hoshoudy [18] [19] . The effects of magnetic field gradient on the Rayleigh-Taylor instability (RTI) with continuous magnetic field and density profiles were analytically investigated by Yang et al. [20] . The analytically and numerically investigated stabilization of the linear growth of the RTI from density gradients, magnetic fields, and quantum effects, in an ideal incompressible magnetized plasma was studied by Wang et al. [21] . Because of the great scientific interest in magnetized plasma problem, it is attempted to discuss the RTI problem of a stratified plasma layer in the presence of an variable magnetic field, where this problem corresponds physically (in astrophysics) to the RTI of an equatorial section of a planetary magnetosphere or of a stellar atmosphere where the magnetic field are perpendicular or parallels to gravity. In all the above-mentioned studies the behaviour of growth rates is considered in the presence of a variable magnetic field in  direction only or in
direction only or in  direction only. Here, the effect of magnetic field in both
direction only. Here, the effect of magnetic field in both  and
and  direction on RTI problem for a finite thickness layer of incompressible plasmas are studied. The dispersion relation is obtained analytically and numerically analyzed.
direction on RTI problem for a finite thickness layer of incompressible plasmas are studied. The dispersion relation is obtained analytically and numerically analyzed.
2. Linearized Equations
We consider the strata of incompressible and inviscous plasma as a fluid of electrons and immobile ions. The plasma is immersed in a magnetic field, where the relevant liner perturbation equations may be written as (Refs. [9] -[17] )
 , (1)
, (1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
Here ,
,  ,
,  and
and , are the perturbations in the velocity
, are the perturbations in the velocity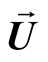 , pressure
, pressure , magnetic field
, magnetic field , and density
, and density , respectively. While
, respectively. While ,
,  ,
,  and the fluid is arranged in horizontal strata, then
and the fluid is arranged in horizontal strata, then  is a function of the vertical coordinate
is a function of the vertical coordinate  only (i.e.
only (i.e. ) and
) and  . Then the system of Equations (1)-(4) become:
. Then the system of Equations (1)-(4) become:
 , (5)
, (5)
 , (6)
, (6)
 , (7)
, (7)
 , (8)
, (8)
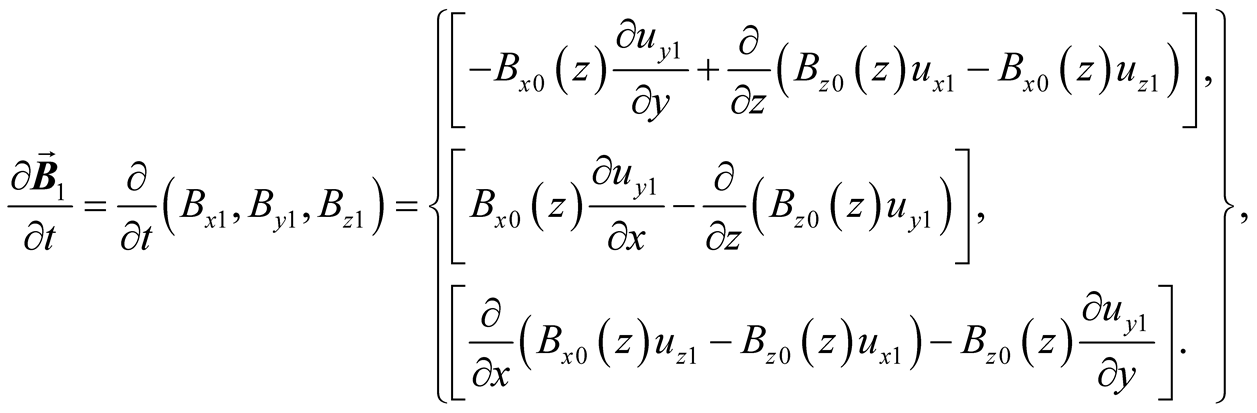 (9)
(9)
 . (10)
. (10)
If we assume that the perturbation in any physical quantity takes the form:
 , (11)
, (11)
where  and
and  are horizontal components of the wave-number vector
are horizontal components of the wave-number vector  such that
such that  and
and  (may be complex
(may be complex ) is the frequency of perturbations or the rate at which the system departs from equilibrium. Using the Expression (11) in the system of Equations (5) - (10), we have:
) is the frequency of perturbations or the rate at which the system departs from equilibrium. Using the Expression (11) in the system of Equations (5) - (10), we have:
 , (12)
, (12)
 , (13)
, (13)
 , (14)
, (14)
 (15)
(15)
 (16)
(16)
 (17)
(17)
Eliminating some variables from the system of Equations (12) - (17) we have:
 (18)
(18)
where,

(19)
3. A Continuously Stratified Plasma Layer
In this section we consider the case of incompressible continuously stratified plasma layer of thickness  units confined between two rigid boundaries, in which the density and magnetic field distribution are given, respectively, by
units confined between two rigid boundaries, in which the density and magnetic field distribution are given, respectively, by ,
, 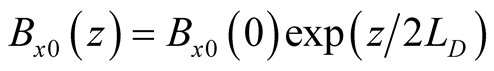 and
and 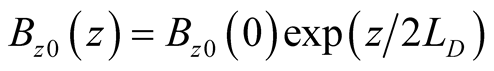 where
where ,
,  and
and  and
and  (the density-scale length) are constants, then Equation (18) takes the form:
(the density-scale length) are constants, then Equation (18) takes the form:
 (20)
(20)
where  and
and 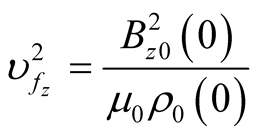 are Alfvén velocity. Now, if we choose
are Alfvén velocity. Now, if we choose  in the form
in the form
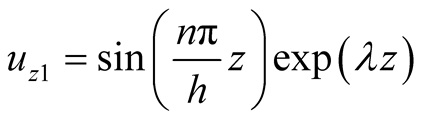 and by substituting in Equation (26), we will have an equation in both
and by substituting in Equation (26), we will have an equation in both  and
and . Then coefficients both
. Then coefficients both  and
and , respectively, are given by:
, respectively, are given by:
 (21)
(21)
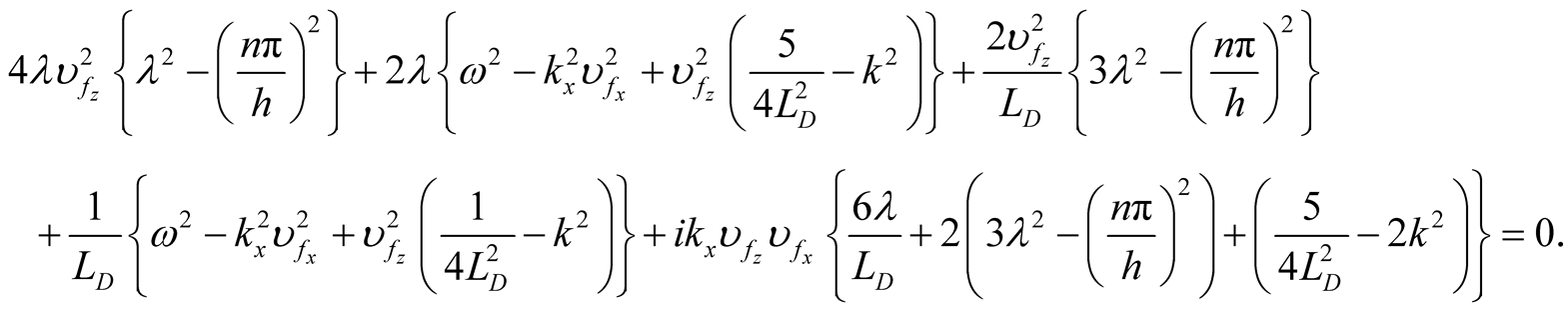 (22)
(22)
Now, we define the dimensionless quantities:
 (23)
(23)
Then Equations (21) and (22), respectively, take the form:
 (24)
(24)
 (25)
(25)
Now, we put  and for
and for  (stable oscillations), then Equations (24) and (25) may be given by:
(stable oscillations), then Equations (24) and (25) may be given by:
 (26)
(26)
 (27)
(27)
To discuss the role of parameter’s problem we consider the next special cases from Equations (26) and (27).
(i) In the case of .
.
From Equation (27) we get , and substituting in Equation (26) we find that the square normalized growth rate given by:
, and substituting in Equation (26) we find that the square normalized growth rate given by:
 , (28)
, (28)
This case is considered by Goldston and Rutherford (see Ref. [9] ), which represents an exponentially growing perturbation (instability case).
(ii) In the case of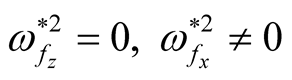 .
.
A second time, from Equation (27) we get , and substituting in Equation (26), then the square normalized growth rate given by:
, and substituting in Equation (26), then the square normalized growth rate given by:
 . (29)
. (29)
This case studied in Refs. ([16] [17] ). It is clarified that, the horizontal magnetic field has stabilizing effect on RTI problem. This influence is obvious from Equations (28) and (29), where,
 . Also, one can see that the square normalized growth rate decreases as
. Also, one can see that the square normalized growth rate decreases as
 increases and the system arrives to complete stability case at
increases and the system arrives to complete stability case at . Now, if we use the relation
. Now, if we use the relation  under the condition
under the condition 
 ,
,  then
then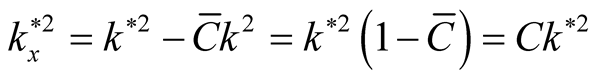 ,
, . Then Equation (29) becomes:
. Then Equation (29) becomes:
 . (30)
. (30)
At , the critical point becomes
, the critical point becomes .
.
This implies that the complete stability happens at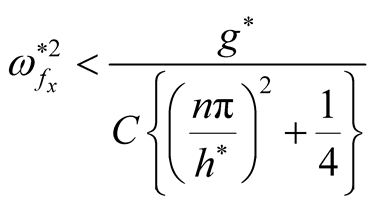 .
.
Also, if the perturbation in the Equation (11) in the form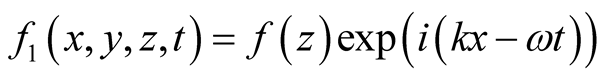 . Then
. Then 
and the square normalized growth rate becomes , and the critical point of stability becomes
, and the critical point of stability becomes  this results correspond with Ref. [17] .
this results correspond with Ref. [17] .
(iii) In the case of . Again, from Equation (27) we get
. Again, from Equation (27) we get , and substituting in Equation (26), the square normalized growth rate given by:
, and substituting in Equation (26), the square normalized growth rate given by:
 . (31)
. (31)
Now, comparing between Equations (28) and (31), someone can observe that, the stabilizing role for the vertical magnetic field on the considerable system, where  and the system arrives to complete stability case at
and the system arrives to complete stability case at . This indicates that, in the presence of
. This indicates that, in the presence of , the stability role stratifies under the condition
, the stability role stratifies under the condition .
.
(iv) For the general case , if we can eliminate the term
, if we can eliminate the term  between Equations (26) and (27). Then the square normalized growth rate given in the from
between Equations (26) and (27). Then the square normalized growth rate given in the from
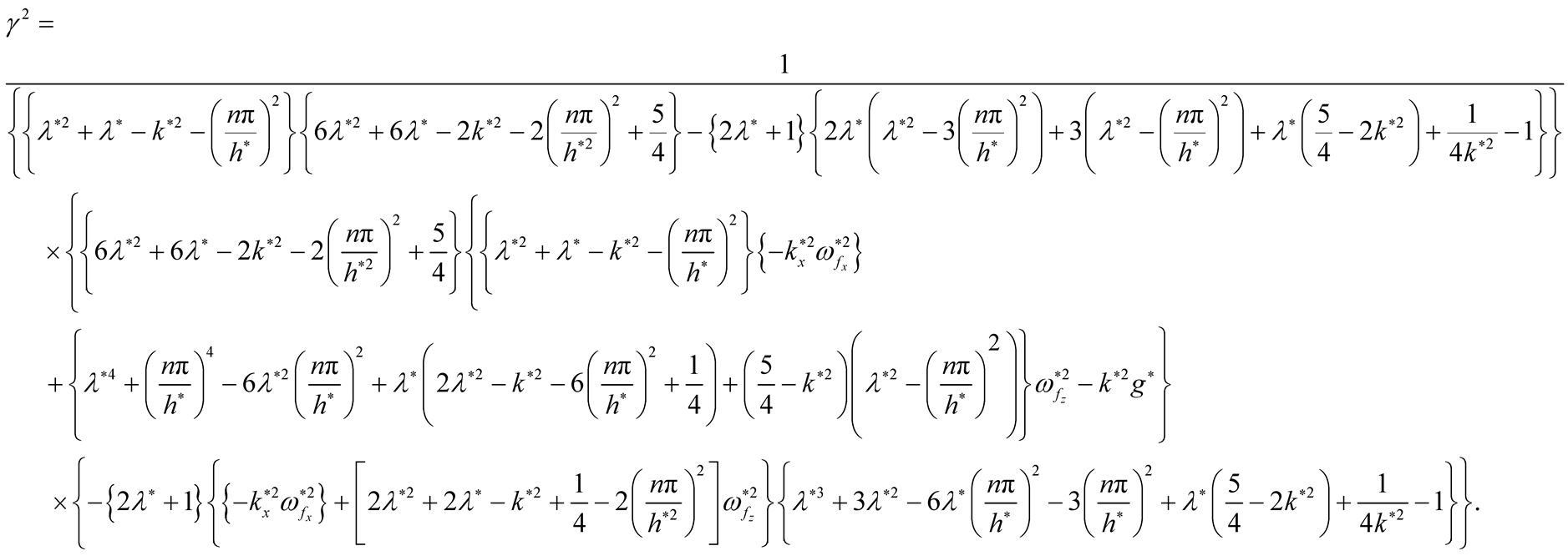
(32)
In the general case, if we wish to look into the effect of both horizontal and vertical magnetic field together on the instability of the considered system, Equation(32) is to be numerically solved, where  is function in the dimensionless quantities of horizontal
is function in the dimensionless quantities of horizontal  and vertical
and vertical  components of the magnetic field, the wave number
components of the magnetic field, the wave number 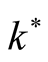 and
and , where
, where  is constant and
is constant and  is the density-scale length. In these figures
is the density-scale length. In these figures ,
,  ,
, 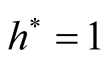 ,
,  and
and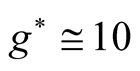 .
.
The role of  as a function horizontal
as a function horizontal  in the presence of both horizontal and vertical magnetic field components
in the presence of both horizontal and vertical magnetic field components  is plotted in Figure 1 and Figure 2, where the square normalized growth rate
is plotted in Figure 1 and Figure 2, where the square normalized growth rate
 is plotted against the square normalized wave number
is plotted against the square normalized wave number . Figure 1(a) shows the role of
. Figure 1(a) shows the role of
 , for example
, for example . One can see that
. One can see that  decrease with increasing of
decrease with increasing of . While Figure 1(b) shows the role of
. While Figure 1(b) shows the role of 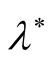
 or
or , where
, where  decrease with decreasing of
decrease with decreasing of . These implies that the maximum instability in the presence of both vertical and horizontal magnetic field happens at
. These implies that the maximum instability in the presence of both vertical and horizontal magnetic field happens at . The same phenomenon hold in Figure 2(a) and Figure 2(b) at
. The same phenomenon hold in Figure 2(a) and Figure 2(b) at . In this case, if we put
. In this case, if we put  in Equation (32), then the maximum square normalized growth rate
in Equation (32), then the maximum square normalized growth rate  is:
is:
 (33)
(33)
From Equation (33) it can see that, the maximum square normalized growth rate  (in the presence of both horizontal and vertical magnetic field components) given as we add the second term in Equations (29) and (31) to Equation (28). Figure 3 shows the role of both horizontal and vertical components’ magnetic field
(in the presence of both horizontal and vertical magnetic field components) given as we add the second term in Equations (29) and (31) to Equation (28). Figure 3 shows the role of both horizontal and vertical components’ magnetic field  on the considered system at
on the considered system at , where the square normalized growth rate
, where the square normalized growth rate  is plotted against the square normalized wave number
is plotted against the square normalized wave number . One can see that, the magnitudes of
. One can see that, the magnitudes of  in the presence of these parameters
in the presence of these parameters  or either them is less than their magnitudes in the Goldston and Rutherford case, which means that these factors have a stabilizing effect on the considered system. Also, it can seen that, no mode of maximum instability exists when
or either them is less than their magnitudes in the Goldston and Rutherford case, which means that these factors have a stabilizing effect on the considered system. Also, it can seen that, no mode of maximum instability exists when  as the square normalized growth rate
as the square normalized growth rate  usually increases by increase with the square normalized wave number values. While, in the presence of quantum term
usually increases by increase with the square normalized wave number values. While, in the presence of quantum term , there is a mode of maximum instability, where the square normalized growth rate
, there is a mode of maximum instability, where the square normalized growth rate  increases with
increases with  increases through the range
increases through the range 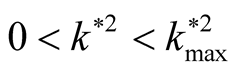 (at
(at  the square normalized growth rate arrives to the maximum instability, and when
the square normalized growth rate arrives to the maximum instability, and when  the square normalized growth rate
the square normalized growth rate  starts to decreases as
starts to decreases as  increases and then goes to the complete stable at
increases and then goes to the complete stable at 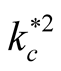 (
(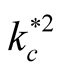 is the critical value for stability, at this point the square normalized growth rate goes to zero). This means that the horizontal component of magnetic field has a crucial capability to suppress the instability that satisfies for the large wave number (short wavelength), while the vertical component of magnetic field has this strength just for the very short wave number (large wavelength). Also, the considerable model is more stability in the presence of both horizontal and vertical components of the magnetic field
is the critical value for stability, at this point the square normalized growth rate goes to zero). This means that the horizontal component of magnetic field has a crucial capability to suppress the instability that satisfies for the large wave number (short wavelength), while the vertical component of magnetic field has this strength just for the very short wave number (large wavelength). Also, the considerable model is more stability in the presence of both horizontal and vertical components of the magnetic field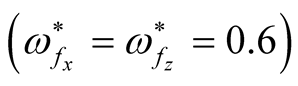 . This case
. This case  shows in Figure 4, where the magnitudes of
shows in Figure 4, where the magnitudes of  decrease with increasing of both horizontal and vertical components of magnetic field
decrease with increasing of both horizontal and vertical components of magnetic field
 that are less than their counterpart at
that are less than their counterpart at  (Goldston and Rutherford results). Figure 5(a) and Figure 5(b) show the role of magnetic field
(Goldston and Rutherford results). Figure 5(a) and Figure 5(b) show the role of magnetic field  when
when  have
have
different values than  (at
(at , respectively). In Figure 5(a), one can see that, the maximum instability (maximum square of growth rate
, respectively). In Figure 5(a), one can see that, the maximum instability (maximum square of growth rate ) at
) at  in Figure 5(a), respectively, are
in Figure 5(a), respectively, are , they are less than their counterpart in Figure 4
, they are less than their counterpart in Figure 4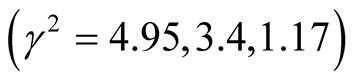 . Also, the critical point for stability in Figure 5(a), respectively, are
. Also, the critical point for stability in Figure 5(a), respectively, are , they are less than their counterpart in Figure 4
, they are less than their counterpart in Figure 4 . This implies that the magnitudes of
. This implies that the magnitudes of  in Figure 5(a) at
in Figure 5(a) at  are less than their counterpart in Figure 4 at
are less than their counterpart in Figure 4 at . The same phenomenon holds in Figure 5(b) but at
. The same phenomenon holds in Figure 5(b) but at , where both the maximum instability and the critical point for stability in Figure 5(b) are less than their counterpart in Figure 4 at
, where both the maximum instability and the critical point for stability in Figure 5(b) are less than their counterpart in Figure 4 at , which also indicates that, the magnitudes of
, which also indicates that, the magnitudes of  at
at  are less than their counterpart at
are less than their counterpart at .
.
4. Conclusions
Finally, we have investigated the effect of magnetic field in both horizontal and vertical direction on the Rayleigh-Taylor instability of stratified incompressible plasmas layer. We can summarize the results as follows:
(i) In the presence of horizontal magnetic field only or vertical magnetic field only the growth rate depends on
 of plasma layer and
of plasma layer and  takes one value
takes one value . While, in the presence of both horizontal and vertical magnetic field, the square growth rate (Equation (32)) depends on the dimensionless thickness
. While, in the presence of both horizontal and vertical magnetic field, the square growth rate (Equation (32)) depends on the dimensionless thickness 
and also depends on the parameter .
.
(ii) The constant  plays an important stabilizing role in the growth rate, where the maximum instability happens at
plays an important stabilizing role in the growth rate, where the maximum instability happens at  and to get more stability model, the values
and to get more stability model, the values  must be different than
must be different than  (i.e.
(i.e.  or
or ). In other words, in studying the combined effect of horizontal and vertical magnetic field on RTI of stratified plasma, the system will be more stable when we accept that
). In other words, in studying the combined effect of horizontal and vertical magnetic field on RTI of stratified plasma, the system will be more stable when we accept that  is different than −0.5 (i.e.
is different than −0.5 (i.e. ).
).
(iii) Our model is more stable than those considered in previous study (horizontal magnetic field only or vertical magnetic field only). This divergence ascribes to the stabilizing role that the magnetic field plays on RTI problem in the presence of both horizontal and vertical components, where the presence of both these parameters dissipates the energy of any disturbance and thereby the system becomes more stability.