Brief Note on a Scalar Quantum Field with Finite Lifetime in a Lorentz Invariant Non-Rectangular Euclidean Space ()
1. Introduction
Ultraviolet (UV) divergences in quantum field theories (QFTs) without regularization and renormalization occur because of short-distance interactions between the elementary particles. These interactions are considered in the high energy range of loop-momentum integrals. A well-known example for this behavior is the one loop-momentum integral of the scalar QFT with a j4 potential term to simulate self-interacting. Although, this theory must be seen as an artificial test model, we know that a scalar field is related to the Higgs boson [1] [2] . If one assumes a very small coupling constant for the j4 potential, the dressed propagator D(x1, x2) is given by the one-loop approximation and consists of the free field propagator D(x1, x2), and the tadpole diagram (Figure 1).
An analysis of the momentum integral corresponding to the tadpole diagram shows that its divergence degree is +2. In order to calculate the corrected mass and lifetime of the self-interacting scalar field a regularization and renormalization procedure is needed. In general, the divergences in loop-momentum integrals originate from the fact, that special QFTs, e.g. quantum electrodynamics, are low energy approximations of a complete theory of all possible quantum particle interactions, including gravity [3] . In this study it is asked whether there is chance to simplify the regularization and renormalization procedure. As a first step to seek an answer to this question, the upper dressed propagation operator defined in Figure 1 is computed with a modified method. This method requires a split of the integration range using the Planckian mass,  where EP = 1.22 × 1019 GeV is the Planck energy. The related split value is
where EP = 1.22 × 1019 GeV is the Planck energy. The related split value is . Accordingly, one gets for the spatial frequency k = 2p/l or if we consider the particle masses of real and virtual particles k = 2pl where l is the inverse Compton length l = m0×c/ħ• a low energy sector (LES) with
. Accordingly, one gets for the spatial frequency k = 2p/l or if we consider the particle masses of real and virtual particles k = 2pl where l is the inverse Compton length l = m0×c/ħ• a low energy sector (LES) with , i.e. Lorentz invariance of measurable (scalar) values, and
, i.e. Lorentz invariance of measurable (scalar) values, and
• a high energy sector (HES) with , i.e. Lorentz symmetry is broken.
, i.e. Lorentz symmetry is broken.
Actually, between the energy sector of standard QFT and the HES an appropriate transition region might exist, since it is speculated that the effects related to the violation of Lorentz invariance (e.g. polarization independent refractivity [4] ) can already be detected at energies much lower than EP = mPc2. Nonetheless, it will be shown in section 3 that for the simple scalar quantum field a sharp separation works well.
Because an interval split is useless if one integrates over both energy intervals with the same method, an integration measure needs to be derived that differs between LES and HES. This measure shall reflect the lower retrievable information content of the HES compared to the LES. The next two sections explain how this measure is derived and implemented mathematically. In Section 4, the modified method of computing loop integrals is applied to the tadpole integral illustrated in Figure 1. Lastly, the applicability of this integration method is discussed and further steps to establish this technique are outlined.
2. Invariance of Lorentz Transformation in the Non-Rectangular Euclidean Space
It is assumed that the integration measure directly related to the geometry of Minkowski space (MS) may not be appropriate for the calculation of the high energy range of momentum integrals. Therefore, an alternative, Lorentz invariant, geometry is constructed. It turns out that a non-rectangular space with Euclidean signature and an energy dependent angle between its space and time axes can be used. This non-rectangularity is useful to obtain an energy dependent integration measure. In this space, which is abbreviated by NoNRES (see section 3), one has general transformations given by
 (1)
(1)
between an inertial system S moving with the velocity v = Vjej and an inertial system S‘ moving with a velocity . The index j is arbitrary but fixed. Further one sets
. The index j is arbitrary but fixed. Further one sets ,
,  ,
,  for k ¹ j. As for the MS the scalar product of vector
for k ¹ j. As for the MS the scalar product of vector  is Lorentz invariant, i.e.,
is Lorentz invariant, i.e.,
 (2)
(2)

Figure 1. Two Feynman diagrams (right-hand side) giving the first order dressed propagator (left-hand side) of the weakly self-interacting scalar field, j.
where the matrix  describes the Lorentz transformation (LT) and gab (g¢mn) is the metric tensor in the NoNRES. From Equation (2) we obtain
describes the Lorentz transformation (LT) and gab (g¢mn) is the metric tensor in the NoNRES. From Equation (2) we obtain
 (3)
(3)
The parameter sj depend on the velocity ratios  and
and  where j = 1, 2, 3 is arbitrary but fixed. If one assumes for sj and wj a relation typical for the LT, all the non-zero elements of
where j = 1, 2, 3 is arbitrary but fixed. If one assumes for sj and wj a relation typical for the LT, all the non-zero elements of  can be written according to Equation (1) in the following way
can be written according to Equation (1) in the following way
 (4)
(4)
All off-diagonal elements of the metric g0j  in the NoNRES are related to the angle between the axis xj
in the NoNRES are related to the angle between the axis xj  and x0
and x0 , which is influenced by the ratio bj
, which is influenced by the ratio bj . Based on these assumptions one obtains for the elements of gmn
. Based on these assumptions one obtains for the elements of gmn
 (5)
(5)
The equivalent approach follows for the metric g'mn in S' using the coefficients  and
and . When S is an inertial system for a resting body its metric gmn = dmn with dmn = 1 if m = n and dmn = 0 if m ¹ n. An expression that relates rj and
. When S is an inertial system for a resting body its metric gmn = dmn with dmn = 1 if m = n and dmn = 0 if m ¹ n. An expression that relates rj and  to sj can be derived inserting the Equations (4) and (5) into Equation (3):
to sj can be derived inserting the Equations (4) and (5) into Equation (3):
 (6)
(6)
Because the absolute value  occurs in Equation (4) there are two solutions for Equation (6)
occurs in Equation (4) there are two solutions for Equation (6)
 (7)
(7)
We note that  and
and . The relations in Equation (7) correspond to the addition theorems of the velocity ratios bj and
. The relations in Equation (7) correspond to the addition theorems of the velocity ratios bj and . To show this, we need to express
. To show this, we need to express  and
and  by bj
by bj . It follows from Equation (5) that rj = 0 and lj = 1 for a system at rest, S. Equation (7) simplifies to
. It follows from Equation (5) that rj = 0 and lj = 1 for a system at rest, S. Equation (7) simplifies to
 (8.1)
(8.1)
where the index 0 indicates that one inertial system, S, is at rest. The two plots in Figure 2 present the inverse function, i.e., the curves of  and
and  versus the parameters
versus the parameters  and
and . It is interesting to recognize the increase of
. It is interesting to recognize the increase of 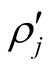 on the left-hand plot and the decrease of
on the left-hand plot and the decrease of  on the right-hand plot.
on the right-hand plot.
This behaviour ensures that the metric given by Equation (5) is real. Now, S' is at rest and S is the inertial system for a moving body. We set ,
,  in Equation (7) and obtain
in Equation (7) and obtain
 (8.2)
(8.2)
Inserting Equations (8.1) and (8.2) into the relation for  and
and  in Equation (7) it can be shown that
in Equation (7) it can be shown that
 (9)
(9)
 (10)
(10)
which are indeed the addition theorems of the velocity ratios known from special relativity in the MS, where parameters  and
and  are equal to bj and
are equal to bj and , while for
, while for  and
and  one finds
one finds  and
and . Note, that matrix
. Note, that matrix  is identical to the LT. In addition, timeand space-like regions can be identified in the NoNRES, which are related to both of the solutions in Equation (7). The first relation in Equations (7) and (9) is the addition theorem of velocities lower than c and the second relation is the addition theorem of velocities higher than c. The index j, that can have values between 1 and 3, gives the three matrices
is identical to the LT. In addition, timeand space-like regions can be identified in the NoNRES, which are related to both of the solutions in Equation (7). The first relation in Equations (7) and (9) is the addition theorem of velocities lower than c and the second relation is the addition theorem of velocities higher than c. The index j, that can have values between 1 and 3, gives the three matrices  in Equation (4) that form the Lorentz group in the NoNRES. In special relativity, a fundamental parameter is the “Eigenzeit” following from the approach
in Equation (4) that form the Lorentz group in the NoNRES. In special relativity, a fundamental parameter is the “Eigenzeit” following from the approach
 (11)
(11)
It agrees with the “Eigenzeit” in the MS and verifies the identity between  and bj (the plus index is suppressed)
and bj (the plus index is suppressed)
 (12)
(12)
Using this “Eigenzeit” the energy-mass relation can be derived. For the particle energy E we obtain
 (13)
(13)
where the vector  is the four-velocity, and the vector p = m0u is the four-momentum, if the particle rest mass is m0. The energy-mass relation in Equation (13) is well-known from special relativity in the MS. Using this equation we express the metric parameter lj as
is the four-velocity, and the vector p = m0u is the four-momentum, if the particle rest mass is m0. The energy-mass relation in Equation (13) is well-known from special relativity in the MS. Using this equation we express the metric parameter lj as
 (14)
(14)
For a particle nearly at rest with E ~ m0c2, the NoNRES becomes almost rectangular, i.e., lj ~ 1 and rj ~ 0. From Equation (14) it is clear that the angle between the time and the relevant space axis in S depends on the particle energy, just as required at the beginning of this section. If the particle energy of the quantum field influences the metric attached to it, the NoNRES cannot be globally an Euclidean space, Rn, where n = 4. It seems rather to be a manifold, Mn, that is locally isomorphic to Rn. The corresponding local positions in the NoNRES are infinitesimal small regions in space and time given by the interaction events between the quantum fields.
In the following section we derive the effective dimension of the NoNRES and describe the consequences of the geometry for this number. The effective dimension is a key ingredient for the desired integration measures allowing a low-weighted consideration of the high energy sector.
3. The Effective Dimension of the NoNRES
Using Equation (2) we can transform any inertial system in the NoNRES into a rectangular Euclidean space. However, doing so requires a continuous space-time with a well-defined metric. For energies in the Planckian range space-time fluctuations occur [4] (which may cause the polarization independent refractivity [5] ) and this condition is not fulfilled. Since Equation (2) can be understood as a symmetry, where the related group is the Lorentz group, the emergence of the non-continuous space-time structure leads to a violation of Equation (2) and thus to a broken Lorentz symmetry. In the upper energy range of the LES and in the HES fluctuations have to be expected, if a virtual (off-shell) particle with an energy near the Planckian range interacts with a real (on-shell) or another virtual particle. They cause uncertainties for the physical parameters containing expressions like gmnkmkn or with similar terms. Because of Equation (13) the value of rj approaches 1 if the particle energy tends to infinity. Accordingly, the angle between the space and time axis decreases to 0˚. Moreover, all the other spatial coordinate ranges are correspondingly shrunk compared to the ranges of x0 and xj, since the factor 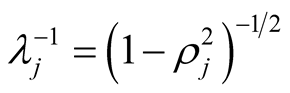 tends to infinity. As a result, the information on the dynamics of the physical parameters is overwhelmed by the metric fluctuations. Due to a broken Lorentz symmetry caused by the non-continuous space-time, the non-rectangularity of the NoNRES becomes manifest in the HES. In the LES it appears to be a transformation effect which does not seriously destroy the accuracy of the theory. Consequently all scalar values can be calculated for a 4-dimensional rectangular space in the LES. In order to consider this geometrical behaviour of our special type of space-time in its name, it is called not necessary rectangular Euclidean space. The information loss for real high quality measurements (i.e. measurements with finite but sufficient accuracy) can be quantified. An appropriate measure to describe the mixing degree of quantum states is von Neumann’s entropy SN given by [6]
tends to infinity. As a result, the information on the dynamics of the physical parameters is overwhelmed by the metric fluctuations. Due to a broken Lorentz symmetry caused by the non-continuous space-time, the non-rectangularity of the NoNRES becomes manifest in the HES. In the LES it appears to be a transformation effect which does not seriously destroy the accuracy of the theory. Consequently all scalar values can be calculated for a 4-dimensional rectangular space in the LES. In order to consider this geometrical behaviour of our special type of space-time in its name, it is called not necessary rectangular Euclidean space. The information loss for real high quality measurements (i.e. measurements with finite but sufficient accuracy) can be quantified. An appropriate measure to describe the mixing degree of quantum states is von Neumann’s entropy SN given by [6]
 (15)
(15)
where j is the density matrix of an ensemble of quantum mechanical states qk. Assuming that the density matrix fulfils the eigenvalue equations: fua = eaua, we can simplify Equation (15) an write:
 (16)
(16)
where ea and (uk)a are the eigenvalues and −vectors of the d × d density matrix f. If the d eigenvalues {ea} with a = 0, d − 1 are normalized as given in Equation (16) they can be linked to the probabilities of the states qk. Then, the von Neumann entropy in Equation (16) agrees with Shannon’s entropy and the related density matrix represents an ensemble of pure states. If one sets for f the metric g of the NoNRES, Shannon’s entropy seems to be useful to derive an effective dimension, dim(g), for the NoNRES even if g in Equation (5) depends on classical observables and not on the equivalent quantum operators (compare to Equation (14)). Using the entropy in Equation (16), one computes the effective dimension dim(g) by the following expression
 (17)
(17)
where the bar indicates normalization of the eigenvalues of the metric. The notation dim[g(E)] =: dim(E) is used to underline the energy dependency of the effective dimension which is caused by the energy dependency of the metric. If dim(E) = 4, the information content of the four vector components is measurable without any loss due to the finite accuracy of the measured data. If dim(E) < 4 uncertainties resulting from measurement errors can increase up to infinity if the smallest eigenvalue approaches zero [7] . According to Equation (5) the eigenvalues of the metric in their normalized form are
 (18)
(18)
If rj = 0, i.e., lj = 1, the eigenvalues are ēa = 1/4 for all a. Thus, the effective dimension dim(E) = 4 and the space-time corresponds to an rectangular Euclidian space, i.e. a coordinate system for a resting particle. For a moving particle one obtains rj > 0, i.e., lj < 1 leading to dim(E) < 4. Inserting Equation (14) into Equation (18) gives
 (18.1)
(18.1)
 (18.2)
(18.2)
 (18.3)
(18.3)
with  (note that the x-axis in Figure 3 presents q = E/E0,) and max(Q) = min(q) = 1. For the usual light elementary particles with masses equivalent to the GeV-energy scale, one obtains for the LES
(note that the x-axis in Figure 3 presents q = E/E0,) and max(Q) = min(q) = 1. For the usual light elementary particles with masses equivalent to the GeV-energy scale, one obtains for the LES , i.e.
, i.e.  and therefore, ē0 ~ 1 and ēa ~ 0 for a > 0. Next, one gets following expression for the entropy SN according to Equation (16)
and therefore, ē0 ~ 1 and ēa ~ 0 for a > 0. Next, one gets following expression for the entropy SN according to Equation (16)
 (16.1)
(16.1)
or
 (16.2)
(16.2)
In Figure 3 the shapes of the effective dimensions, dim(E), versus the energy ratio, E/E0, for three scalar particles with different rest energies are shown. The
 (17')
(17')
For the boundary region of LES one finds that  (note: limQ®0(QQ) = 1) which corresponds to
(note: limQ®0(QQ) = 1) which corresponds to  where
where  (see Figure 3). To facilitate a comparison of the shape of dim(E) for a particle with Higgs mass (left plot of Figure 3) with that of hypothetical super-heavy particles the other two plots are presented. The soft decrease in the middle and right plot of Figure 3 results from the much higher masses of these hypothetical particles.
(see Figure 3). To facilitate a comparison of the shape of dim(E) for a particle with Higgs mass (left plot of Figure 3) with that of hypothetical super-heavy particles the other two plots are presented. The soft decrease in the middle and right plot of Figure 3 results from the much higher masses of these hypothetical particles.
In contrast to the shapes of dim(E) for the super-heavy particles, the information loss calculated for the particle with Higgs mass reaches its limit dim(E) = 1 for an increasing energy very rapidly. Nevertheless, a comparison of the magnitudes of q in the three plots shows, that the different shapes become similar to each other if the number of magnitudes would be the same in all plots of Figure 3. As a consequence, dim(E) differs between particles of different mass while dim(q) is a universal parameter. If Lorentz symmetry exists and the light speed is constant for the complete LES, the total energy of this sector cannot be higher than the Planckian limit, mPc2. Note, that in the left plot of Figure 3 the maximum energy is max(E) ~ 7 ´ 105 EH (with EH = mHc2) and much smaller than the maximum energy in the middle and right plots (with max(E) ~ EP). For an off-shell Higgs particle the dimensional limit is reached long before the quantum fluctuations of the metric become important, the Lorentz symmetry is intact and the LT is applicable even if dim(E) » 1. For off-shell super-heavy particles,
E0 = 1.26 × 102 GeV E0 = 9.50 × 1016 GeV E0 = 1.20 × 1018 GeV
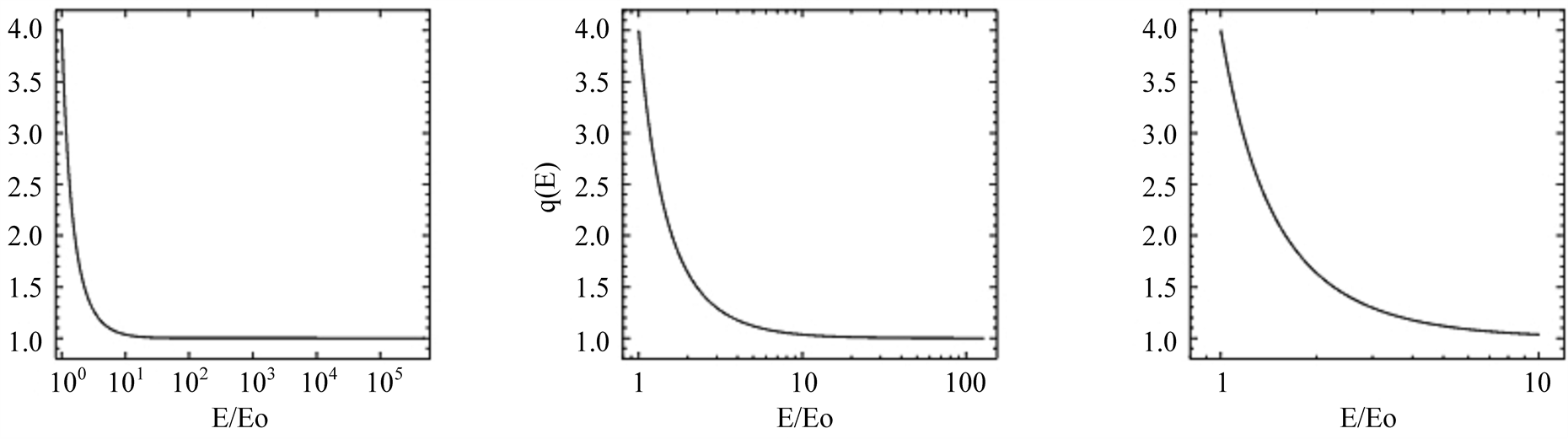
Figure 3. Loss of information, given by the dimension dim(E), between two corresponding inertial systems for a measuring device and a particle. This loss is shown for three particles with different masses in individual plots. Since dim(E) depends on the particle energy, an energy ratio, q = E/E0 is introduced. The rest energy, E0 = m0c2, in the left plot results from the Higgs mass [1] , m0 = mH. In the middle and right plot, E0 corresponds to the mass of hypothetical super-heavy particles close to the Planckian scale. The minimum energy E on the x-axis of each plot varies, since the rest masses differ, but min(q) = 1. The upper boundary value of q is q* = EP/E0 and varies in its value due to the different particle masses..
especially for a particle with a mass m0 ~ mP/10 (right plot of Figure 3) the quantum fluctuations of the metric have started already while dim(E) > 1 and the transformation between inertial systems is not allowed anymore due to the broken Lorentz symmetry.
In the Introduction a transition region between the sector of the standard model is mentioned. For the simple scalar field this transition region needs not to be considered. However, the shapes of dim(E) for the super-heavy particles suggest the existence of some transition region.
4. The Interacting Scalar Particle in the NoNRES
Now, the derived integration measure is used for an interacting scalar quantum field, j. We consider the 4-momentum pm of a free scalar particle and calculate the energy-momentum relation in the NoNRES
 (19)
(19)
which leads to the Klein-Gordon operator À = ¶a¶a + 1 where the inverse Compton length l = m0×c/ħ is used to scale the field j ® j/l and the axes xm ® lxm. For a self-interacting scalar field, j, the action integral A[j, J] is given by
 (20)
(20)
where the potential term is V[j] = w/4!×j4, J is some background field and dim is the dimension of the particle related space-time. In contrast to the MS, the metric factor g1/2 of the NoNRES, occurring in the action, gives 1. Accordingly, the path integral can be written as exp(−A/ħ), unlike exp(−iA/ħ) in the MS. The Green’s function, D(x), of a free scalar field with V[j] = 0 can be calculated from
 (21)
(21)
where kn ® kn/l and ie is a regularization term for the denominator if k2 = 1. The connected 2-point Green’s function (compare to the dressed propagator in Figure 1) for the weakly self-interacting field in the one-loop approximation is given by
 (22)
(22)
The Fourier transform of Equation (22) can be expressed as
 (23)
(23)
Since the interaction given by Equation (20) is sufficiently weak  one can write for Equation (23)
one can write for Equation (23)
 (24)
(24)
where the scaled corrected mass and lifetime of the weakly self-interacting field, j, result from
 (25)
(25)
In the MS D(0) is UV divergent. However, in the NoNRES we obtain a finite expression as shown below. Considering dim = dim(E) the integral for D(0) in Equation (23), which depends on k2 only, is given by
 (26)
(26)
where the integration range of k extends from null to infinity. From this equation the sought integration measure, which is ddim(E)k, can be read off. In the special case of a k2 -dependent integration function, it simplifies to . The integration range is split into the two energy sectors as explained in the Introduction. They go from the k = 0 to Ep/m0c2 and from k = Ep/m0c2 to ¥. If the energy E < EP the physical space is modeled by a 4-dimensional rectangular Euclidean space due to the intact Lorentz symmetry and the applicability of the corresponding LT. If E ~ EP the LT is not allowed anymore. However, dim(E) has reached the limit dim(E) = 1 long before (see Figure 3), thus, we can find a jump function for the effective dimension of the local NoNRES written as
. The integration range is split into the two energy sectors as explained in the Introduction. They go from the k = 0 to Ep/m0c2 and from k = Ep/m0c2 to ¥. If the energy E < EP the physical space is modeled by a 4-dimensional rectangular Euclidean space due to the intact Lorentz symmetry and the applicability of the corresponding LT. If E ~ EP the LT is not allowed anymore. However, dim(E) has reached the limit dim(E) = 1 long before (see Figure 3), thus, we can find a jump function for the effective dimension of the local NoNRES written as
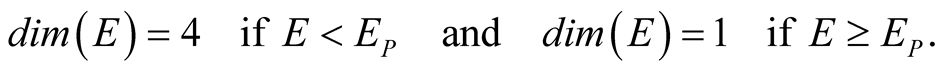 (27)
(27)
Consequently, we obtain for Equation (26)
 (28)
(28)
Both terms are finite and give
 (29)
(29)
Obviously, the effective dimension, dim(E), acts as a “regularization-like parameter” influencing the integration result in the high-energy range. However, in contrast to usual regularization procedures in the MS, dim(E) leads to a convergent result without specific normalization concepts.
Because of scaling we substitute for k* the ratio of Planckian to particle rest energy, i.e., k* = EP/m0c2. Since the generator of the massive scalar field, j, is assumed to be the Higgs particle, it results m0c2 º mHc2 = 126 GeV [1] [2] , where mH is its mass and c is the light speed, as has already been used to calculate the shape of dim(E) presented in Figure 3. Therefore, we obtain for the corrected mass, m*, and the un-scaled lifetime, tL, derived from Equation (25), the following results
 (30)
(30)
 (31)
(31)
The coupling constant should be w £ 10/Js to guarantee the applicability of a first order approximation to re-arrange Equation (23). If the particle mass is not the estimated Higgs mass, but, e.g., the electron mass, we had to require a much lower upper boundary for w or Equation (24) would be invalid. The theory described by Equation (20) is true for massive scalar particles. If one likes to consider massless particles, e.g. photons, together with Higgs scalars, the standard model of the electro-weak and strong interaction needs to be slightly modified to ensure its Lorentz invariance in the NoNRES.
5. Conclusions
The metric, gmn, in the NoNRES, which depends on the particle energy, E, allows to derivate an effective dimension, dim(E), which is the key parameter of the integration measure ddim(E)k. In contrast to the NoNRES, the effective dimension of the MS always gives dimMS(E) = 4 for all values of E, i.e., it is independent of the particle energy. The described integration-method constructed for the NoNRES involves the high energy range of the specific QFT more appropriately than the MS, since the available information content of the observed process is considered and quantified. In addition, the NoNRES can be constructed for space-times of arbitrary dimensions. The results obtained for Equations (30) and (31) are quite reasonable. In contrast to the mass correction, the life time of the particle is mainly influenced by the result of the high energy sector, i.e., the large imaginary part of D(0) in Equation (29).
In this study a self-interacting scalar particle is considered. In order to develop a real QFT in the NoNRES we have to include particles with a larger coupling constant (i.e. higher order loop integrals needs to be taken into account) and particles with a spin larger than 0. Then, QED (quantum electrodynamics) can be studied to model the interaction between electrons by means of photon exchange. In comparison to Equation (20), the QED action integral is more complex and contains the Abelian gauge field, Aa, and a spinor field, y. An extension of our integration method to QED would open the access to real measurements.
Acknowledgements
The author would like to cordially thank Uwe Motschmann from the Institute for Theoretical Physics at the Technical University Braunschweig for many fruitful discussions.