1. Introduction
In this note we consider a numerical method for singular linear boundary value problems. Such problems arise very naturally in various applications including gas dynamics, chemical reactions, and structural mechanics. Traditional methods fail to produce good approximations for such equations. As a result, a number of investigators have considered various non-classical methods, including Chebyshev polynomials, B-splines, and cubic splines [1] -[3] . Recent results also include methods based on reproducing kernel space [4] [5] , and Sinc collocation method [6] .
The purpose of this note is to develop an iterative method for singular and singularly perturbed boundary value problems. The method is explicit in nature, and can be considered to be an iterative predictor-corrector method. Section 2 introduces the method in details. Section 3 provides sufficient conditions for the convergence of the method. Section 4 uses a number of examples to investigate the applicability of the method, and compares the results to exact solutions.
2. An Iterative Method for a Singular Boundary Value Problem
Consider a second-order singular differential equation given by
 (1)
(1)
With Dirichlet-type boundary condition
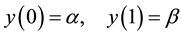 (2)
(2)
where, the functions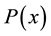 ,
, 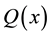 and
and  are analytic in
are analytic in . The functions
. The functions 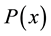 and
and  can vanish at the boundary points. Assume that the domain is divided into
can vanish at the boundary points. Assume that the domain is divided into 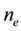 equal intervals
equal intervals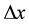 , which leads to
, which leads to 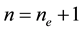 nodes with
nodes with ,
,  , for
, for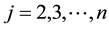 . The boundary conditions provide the values for
. The boundary conditions provide the values for 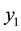 and
and . Consider a finite difference approximation of the above equation given by
. Consider a finite difference approximation of the above equation given by
![]() (3)
(3)
where![]() ,
, ![]() , and
, and![]() . The boundary conditions provide the values for
. The boundary conditions provide the values for ![]() and
and![]() . It is then possible to formulate a two-step iterative formulation. First, using the given boundary conditions, an initial value can be assigned to the unknown function, i.e.
. It is then possible to formulate a two-step iterative formulation. First, using the given boundary conditions, an initial value can be assigned to the unknown function, i.e.![]() ,
,![]() . Starting from the left
. Starting from the left![]() , and marching to the right, the first step is to solve Equation (3) for
, and marching to the right, the first step is to solve Equation (3) for ![]() (here, we are naming it
(here, we are naming it ![]() and refer to it as an intermediate variable) according to
and refer to it as an intermediate variable) according to
![]() (4)
(4)
for ![]()
Note that, marching from the left to right, the above equation is explicit for![]() . The second step is to march from the right to the left according to
. The second step is to march from the right to the left according to
![]() (5)
(5)
For![]() .
.
The variable ![]() is an intermediate variable for which
is an intermediate variable for which ![]() and
and![]() . Marching from right to left, the above equations can be solved for
. Marching from right to left, the above equations can be solved for ![]() explicitly. The above two steps can be repeated after setting
explicitly. The above two steps can be repeated after setting![]() , for
, for![]() . In the next section, we provide sufficient condition for convergence of the above iteration.
. In the next section, we provide sufficient condition for convergence of the above iteration.
3. Convergence of the Method
For simplicity, consider a second-order singular differential equation given by
![]() (6)
(6)
The same analysis can be performed for a non-zero![]() . The above two-step iterative method simplifies to
. The above two-step iterative method simplifies to
![]() (7)
(7)
![]() (8)
(8)
In a matrix form, the first step can be written as
![]() (9)
(9)
where![]() . Similarly, writing the second step in a matrix form leads to
. Similarly, writing the second step in a matrix form leads to
![]() (10)
(10)
The above equations can be written in a more compact form according to
![]() (11)
(11)
![]() (12)
(12)
where, the bold lower case letters indicate vectors corresponding to the above terms. After eliminating the intermediate term ![]() in the above equations one can arrive at the equation given by
in the above equations one can arrive at the equation given by
![]() (13)
(13)
For convergence of the above iteration, it is sufficient that all eigenvalues of the coefficient matrix, i.e.,
![]() be inside the unit circle. The form of the coefficient matrices are such that it is possible to obtain
be inside the unit circle. The form of the coefficient matrices are such that it is possible to obtain
explicit expressions for the inverses. For![]() , we have
, we have
![]() (14)
(14)
Note that matrix ![]() is a lower triangular matrix, and its inverse is also a lower triangular matrix. It is also possible to explicitly compute the triple product
is a lower triangular matrix, and its inverse is also a lower triangular matrix. It is also possible to explicitly compute the triple product
![]() (15)
(15)
The matrix ![]() is an upper triangular and its inverse which is an upper triangular is given by
is an upper triangular and its inverse which is an upper triangular is given by
![]() (16)
(16)
Writing the coefficient matrix in Equation (13) as a product of two matrices according to
![]() (17)
(17)
The first matrix on the right hand side is upper triangular, and the second matrix is lower triangular. The diagonal entries are the eigenvalues and using the spectral radius, it is sufficient to have![]() , for
, for
![]() . or
. or![]() . This condition can be satisfied by choosing a small
. This condition can be satisfied by choosing a small ![]() for bounded values
for bounded values
of![]() .
.
4. Numerical Examples
Example 1: Consider a singular boundary value problem [4] given by
![]() (18)
(18)
The exact solution is given by![]() . Using a second-order accurate finite-difference approximation, the first step of the algorithm which is marching from the left
. Using a second-order accurate finite-difference approximation, the first step of the algorithm which is marching from the left ![]() to the right
to the right ![]() according to
according to
![]() (19)
(19)
The second step is to march back from ![]() to
to ![]() using
using
![]() (20)
(20)
Both steps involve the explicit calculations only. After dividing the domain into equal intervals, Table 1 presents the results at selected points inside the domain and compares their values to the exact solution. The iterations are continued until the results do not change. In all the cases, the error is within the order of the approximation of the finite difference scheme. The relative error in the table is computed according to
![]() (21)
(21)
Example 2: Consider another singular boundary value problem [7] given by
![]() (22)
(22)
The exact solution is given by
![]() (23)
(23)
Dividing the domain into equal intervals and using the above method, Table 2 compares the computed solution with the exact solution at different points in the domain. The computed values are after 90,000 iterations. But the calculations are explicit and pose little burden.
Example 3: Consider a singularly perturbed boundary-value problem [7] given by
![]() (24)
(24)
for which the exact solution is given by
![]() (25)
(25)
This problem is singularly perturbed, and large gradients exist close to the boundaries. The present method can still be used to obtain an accurate solution. Table 3 presents the convergence of the solution close to the left ![]() boundary as a function of the mesh size, and Table 4 presents the convergence close to the right boundary
boundary as a function of the mesh size, and Table 4 presents the convergence close to the right boundary ![]() for
for![]() .
.
The above results are for finite difference approximation with equal intervals. The accuracy of the results can be improved by using a smaller mesh sizes close to the boundaries. However, the calculations are explicit and using equal intervals does not pose a computational burden.
5. Conclusions
In this note we presented a numerical method for obtaining the solution of linear singular boundary value prob-
![]()
Table 1. Computed value and the relative error at different values of x.
![]()
Table 2. Computed value and the relative error at different values of x for Example 2.
![]()
Table 3. Computed values and comparison to the exact solution close to x = 0.
![]()
Table 4. Computed values and comparison to the exact solution close to x = 1.
lems. The method can be considered as an iterative predictor-corrector method. Sufficient conditions for the convergence of the iteration was also presented. The proposed method is fully explicit and requires little computational time. It can also be applied to singularly perturbed boundary value problems.
Three numerical examples were used to study the applicability of the method.