The Cost Efficiency of Regional Public Hospitals in South Korea ()
1. Introduction
Increasing health care spending will negatively affect the nation’s economy indirectly [1] . According to an OECD (Organization for Economic Cooperation and Development) report, total health care expenditure in South Korea has been increased steadily since 2001, from 5.2% (35 trillion won) of GDP in 2001 to 7.5% (80 trillion won) of GDP in 2009 (OECD, 2009) [2] . There are many factors that affect the national health sector, however, expenditures from hospitals are the main factor driving this increased [3] . Many developed countries have made an effort to restrain rising health costs by regulating over-investment in medical equipment for hospitals. The prudent purchase of equipment can have an effect on controlling the increase in medical expenses (Park and Park, 2007) [4] .
In South Korea, the plans of management improvement for hospitals have been at the center of a heated debate since IMF crisis1. Budget deficits, in private as well as public hospitals have increased since that time. The managerial expenses of regional, public hospitals, has in addition been adding to the overall deficit and the losses in managerial costs have not been recovered2. Nevertheless, the regional public hospitals cannot stop their operation due to operating deficits, unlike their private counterparts because the services provided from regional public hospitals is closely related to the healthcare of the public3. The deficit, however, cannot be absorbed by poor local governments. The municipalities, whose financial independence is relatively secure, have steadily supported the regional public hospitals while the poorer communities, who lack financial independence have not been able to provide such support. This has led to the accumulation of liabilities without available resources to cover them.
In the view of the situation these hospitals have encountered, it is imperative that they reduce their managerial inefficiencies which would contribute to increased efficiency of the hospitals overall.
To analyze the economic performance of the regional public hospitals, it is necessary to take into account special services provided by these hospitals such as the treatment of foreign workers, senior citizens who live alone, low-income classes and others so situated. Hence, it is important to develop a more realistic and objective estimation method for determining economic performance given the broader responsibilities and costs which are endemic to the public nature of these hospitals.
Regarding a result-oriented economic performance for hospitals, the issue of the efficiency is an important matter. Especially for the public hospitals, it can be a useful tool for analyzing the level of improvement of their efficiency under the resource limitation. Furthermore, seeking for the efficiency through cost-saving measures can lead to improve the competitiveness of these hospitals.
Comparative cost analysis of hospitals was first introduced by Cohen (1967) [5] , Feldstein (1968) [6] , Lave and Lave (1970) [7] , Lave, Lave and Silverman (1972) [8] , taking into consideration the hospital differences, in terms of size, patients’ case mix, and the severity of the diseases treated. Cohen (1967) investigated cost variations in size among general, “short-term” hospitals, and found that hospitals between 150 and 350 beds are most efficient for ordinary patient care. Lave, Lave and Silverman (1972) developed a cost function analysis including case-mix patterns in hospitals, and estimated that the marginal cost of a case is 68 percent of average cost, that there are no significant economies of scale. Newhouse (1970) [9] , and Evans (1971) [10] , analyzed economic performances of non-profit organizations. While Evans (1971) suggested a concept of “behavioral” cost function for non-profit hospitals, Newhouse (1970) applied an economic model to the analysis of non-profit institution. Barry (1976) [11] analyzed an economic framework for examining the utilization of short-term general hospitals with three variables such as the bed rate (the number of beds per thousand population), the occupancy rate (the average bed is occupied), and the admission rate (the number of admissions per thousand population) in Standard Metropolitan Statistical Areas (SMSAs) in 1967. Bays (1980) [12] examined the errors on the specification modeling of the hospital cost functions, and pointed out that a physician variable should be considered, when it comes to the cost function of hospitals. A large number of empirical studies of the economies of scale and scope in hospital services production reported by Aletras et al. (1997) [13] indicate that there were few economies of scale in hospitals beyond 200-300 beds. Prior and Solà (2001) [14] found strong economies of scope or economies of diversification in Catalan hospitals using the data from 1987 to 1992. Exploring scope economies by cost frontier along three different dimensions, Kittelsen and Magnussen (2003) [15] also found strong economies for surgical and medical services, intermediate for inpatient and outpatient production, while elective and emergency care cases have only weak economies of scope.
In South Korea, most previous studies have mainly focused on the efficiency of hospitals. Yang et al. (1997) [16] measured technical efficiency of 31 tertiary hospitals using both CCR (Charnes, Cooper and Rhodes, 1978) [17] and BCC (Banker, Charnes, and Cooper, 1984) [18] models, finding that 13 out of 31 hospitals were efficient by using BCC model, and the financial status was not related with hospitals’ efficiency while the size, quality of care, value added per capita, and revenue per patient were related with their efficiency. Kim (2005) [19] explored the technical efficiency of 135 general hospitals and the determinants of their efficiency using the two-part model over Tobit, showing that the efficiencies of the public hospitals were much lower than those of private hospitals. Yoo (2007) [20] suggested the methodology to improve the measurement of the efficiency for public hospitals using DEA, and emphasizing that the environmental variables such as population should be controlled, and slacks-based measure of efficiency (SBM) should be considered not only to solve the problems of the previous studies but also to estimate the efficiencies more precisely. In 2011, the author examined the unit root and co-intergration tests on the fiscal revenue and spending of Gunsan regional public hospital from 2003 to 2010, stressing that the hospital should focus on the fiscal health since there was no equilibrium relation for a long-run between the fiscal revenue and spending [21] . As we mentioned earlier, the analysis about hospitals has conducted in a various ways, however, most studies of domestic hospitals have mainly focused on the financial structure or technical efficiency analysis over the hospitals. Moreover, it is hard to obtain the data from hospitals in South Korea, particularly wage data of hospitals, and the reliability of this data is questionable. In this context, this paper is significant for being the first to utilize DEA for estimating the cost efficiency, into allocative and technical efficiencies as well as deriving the scale efficiency. In addition, this study uses the inside data such as year payroll, which gives more proper information about wage per doctor and nurse for each regional public hospital for enhancing the reliability of the data.
The aim of this study is to estimate the cost efficiency of the regional public hospitals in South Korea from 2007 to 2010, considering the public achievement for the disadvantaged by hiring the number of patients as output, utilizing DEA4. The remainder of this paper is organized as follows: Section 2 explains a theoretical model of hospitals based on DEA. Section 3 presents data and empirical result, and Section 4 concludes with discussion.
2. Theoretical Model
DEA, a non-parametric method, does not assume the specific functional form to estimate the parameters. It derives the efficient frontier using the observational data for the input and output of production units based on linear programming, and measures the inefficiency by checking how production units are far from the efficient frontier. Charnes, Cooper, and Rhodes (1978) introduced DEA. The authors newly utilized the concept of Farrell's relative efficiency [22] , and developed it as the ratio model between multiple inputs and multiple outputs, which is called CCR model. It assumes that production units operates under constant returns to scale, and decomposes cost efficiency of a production unit into allocative efficiency and technical efficiency. Since this model does not distinguish scale efficiency from the technical efficiency, the technical efficiency might be overestimated. To solve this kind of problem, Banker, Charnes, and Cooper (1984) have worked to develop a separate measure to determine pure technical efficiency assuming variable returns to scale, which is called BCC model. The scale efficiency, then, can be calculated by measuring the ratio between the technical efficiency of CCR model and the pure technical efficiency of BCC model.
Recently, DEA has been widely applied in performance evaluation or benchmarking of production units in regardless of areas such as banks, firms, hospitals and schools since it uses mathematical programming models without a priori assumptions. In this study, we estimate the several efficiencies of the regional public hospitals as their economic performance based on the CCR model. After explaining input-oriented efficiency of these hospitals, the cost minimization issue of the hospitals will be discussed.
2.1. Input-Oriented Efficiency of Hospitals
Let us consider that the technology set of a hospital is defined as follows:
 (1)
(1)
Equation (2) assumes that the input set,  , of the hospital is defined for any output,
, of the hospital is defined for any output, 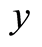 , and the technology set,
, and the technology set, 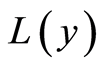 , is as follows:
, is as follows:
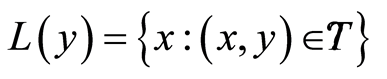 (2)
(2)
Let us suppose that input prices 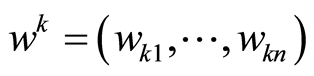 are known for each hospital. If we learn input prices and input quantities, we can estimate total cost
are known for each hospital. If we learn input prices and input quantities, we can estimate total cost 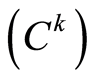 for each hospital,
for each hospital,  , and it can be defined as follows;
, and it can be defined as follows;
 . (3)
. (3)
where  denotes input prices corresponded by wage per doctor, wage per nurse, price of bed, and price of capital, and
denotes input prices corresponded by wage per doctor, wage per nurse, price of bed, and price of capital, and 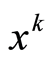 denotes input variables represented by number of doctors, number of nurses, capital stock, and number of operating beds in a hospital. This cost function assumes that a hospital minimizes the total cost, given the input prices and its quantities such as the capital stock, the number of doctors and nurses, and the number of operating beds.
denotes input variables represented by number of doctors, number of nurses, capital stock, and number of operating beds in a hospital. This cost function assumes that a hospital minimizes the total cost, given the input prices and its quantities such as the capital stock, the number of doctors and nurses, and the number of operating beds.
2.2. The Cost Minimization of Hospitals
If we assume constant returns to scale (CRS) with strong disposability of inputs5 in the following equation (represented by C, S), the expression of the cost minimization of the hospital is defined as follows:
C, S), the expression of the cost minimization of the hospital is defined as follows:
 . (4)
. (4)
In general, economists define technical efficiency the same way as Farrell (1957) did. Farrell defined that the efficiency of a production unit is constructed by price (allocative) efficiency and technical efficiency, and proposed that these two efficiencies are integrated to provide a measure of overall (cost) efficiency. The cost (overall) efficiency can be simply divided into two components, i.e., allocative efficiency and the technical efficiency. This is shown below.
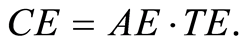 (5)
(5)
In Equation (5), CE, AE, and TE indicate the cost efficiency, the allocative efficiency, and the technical efficiency, respectively. As seen in the Equation (5), the cost efficiency is a combination of the technical efficiency and allocative efficiency. This can be explained more easily by figures.
Figure 1 shows the typical framework by Farrell which let it, possible to decompose the overall efficiency into the technical and allocative efficiencies6. Suppose the case of one output  that is produced by using
that is produced by using

Figure 1. Technical, allocative, and overall efficiency.
two inputs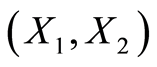 ,
, . Under the assumption of
. Under the assumption of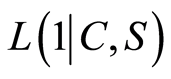 , the efficient unit iso-quant shows all technically efficient combinations. Points such S, Q, and T on the frontier of
, the efficient unit iso-quant shows all technically efficient combinations. Points such S, Q, and T on the frontier of  are technically efficient, however, only T can be technically efficient at minimum cost. In Figure 1, the overall efficiency (OR/OP) can be expressed as the product of technical and allocative efficiencies. The technical efficiency indicates the ratio between optimal and observed actual resource use (OQ/OP). By taking into account the iso-cost line (representing relative factor prices), we can identify allocative efficiency. Allocative efficiency can be represented as the ratio between minimum and actual cost (OR/OQ).
are technically efficient, however, only T can be technically efficient at minimum cost. In Figure 1, the overall efficiency (OR/OP) can be expressed as the product of technical and allocative efficiencies. The technical efficiency indicates the ratio between optimal and observed actual resource use (OQ/OP). By taking into account the iso-cost line (representing relative factor prices), we can identify allocative efficiency. Allocative efficiency can be represented as the ratio between minimum and actual cost (OR/OQ).
Since DEA is a linear programming for estimating the relative performance of a decision making unit, we need to transform the DEA mathematical model into the linear programming formulation for given the input prices and input quantities. This is as follows:
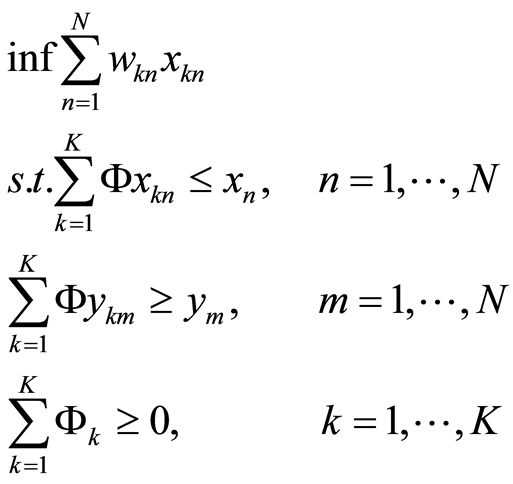 . (6)
. (6)
In Equation (6),  means input prices corresponded by wage per doctor, wage per nurse, price of bed, and price of capital of
means input prices corresponded by wage per doctor, wage per nurse, price of bed, and price of capital of 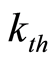 hospital.
hospital.  and
and 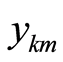 denote minimum input and maximum output of
denote minimum input and maximum output of 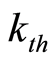 hospital, respectively.
hospital, respectively. 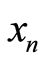 and
and  represent observed actual input and observed actual output of
represent observed actual input and observed actual output of  hospital, respectively.
hospital, respectively.  is a weighted density vector. Here, the weighted density vector is non-negative, and it represents the constant returns to scale7.
is a weighted density vector. Here, the weighted density vector is non-negative, and it represents the constant returns to scale7.
3. Data and Empirical Result
3.1. Data
The data is obtained from financial statements (Balance sheets & Income statements) and final accounts from The Korean Association of Regional Public Hospitals (KARPH) during the period from 2007 to 2010. The total cost of a hospital has been used as a dependent variable in the model. It is measured as a sum of the recurrent cost of the hospital in a given year. The variable, adjusted number of patients is used as a measure of output. The adjusted number of patients includes total number of outpatients and total number of inpatients in a given year. In this study, numbers of doctors, nurses, and beds are used as inputs. Capital stock (tangible fixed assets) is utilized as a fixed input, which excludes depreciation. Tangible fixed assets include land, buildings, land improvements, machinery, delivery equipment or vehicles, medical equipment, equipment, and construction in progress, but exclude accumulated amount of depreciation. All price variables are expressed in real terms at constant price of year 2010 using Consumer Price Index (CPI).
The method to estimate these variables are shown in Table 1, and the descriptive statistics of 34 regional public hospitals during the same time period is illustrated in Table2
3.2. Empirical Result
Table 3 represents cost efficiency (CE), allocative efficiency (AE), and technical efficiency (TE) of the regional public hospitals under CRS technology. According to Table 3, the cost efficiency, allocative efficiency, and technical efficiency of the whole regional public hospitals on average are 0.52, 0.71, and 0.74, respectively. It implies that although more than half of the hospitals are relatively efficient allocatively and technically, they have not been good at selecting the cost-minimal input mix.
Taking a closer look, in terms of the cost efficiency, as the average of the 34 regional public hospitals shows 0.52, there is 48% of the cost inefficiency during the same period. It indicates that there is a possibility to improve its overall economic inefficiency from 15% to 67% in keeping the current level of production by remov

Table 1 .Method to estimate variables.
AP, TC, ND, NN, and TFA mean adjusted number of patients, total cost, number of doctors, number of nurses, and tangible fixed assets, respectively.

Table 2. Descriptive statistics.
*is expressed at constant prices of 2010 using Consumer Price Index (CPI), and its unit used here is million won.
ing the factor of the cost inefficiency. Jeju (0.85) is ranked first, and Chungju (0.71), Seoul (0.70), Anseong (0.70), and Paju (0.70) are following in order after Jeju. Not only the cost efficiency gap between the first and the last, but also the gap between the first and the second among these hospitals is quite big, which are 52% and 15%, respectively. It also indicates that there is no regional public hospital, which fully achieves the overall cost minimization, and most of these hospitals are far away from the optimal cost obtainable from the existing technology.
With respect to the allocative efficiency, Jeju (0.85) still shows the highest level of the efficiency, and Seoul is ranked second. As the allocative efficiency for an individual hospital shows from 0.57 to 0.85, it indicates that there is a possibility to decrease its allocative inefficiency from 15% to 43% by reallocating the input mix. Although Suncheon, Jinju, Uljin, and Gongju, and Daegu show relatively low level of the cost efficiency, which is lower than 0.40, they show much higher level in terms of the allocative efficiency. It represents that these hospitals are comparatively better at allocating the input mix than choosing the cost-saving input mix since the allocative efficiency describes the skill of a production unit in achieving the optimal input, given its price and the production technology while the cost efficiency is the ratio of the optimal cost feasible from the present technology to the actual cost. It also represents that there is no regional public hospital, which completely achieves the goal of choosing input prices in order to minimize the cost, and most of these hospitals are allocatively inefficient for a given level of output and input prices.
When assessing technical efficiency, Jeju shows the maximum efficiency (1.00), and Paju (0.97), Chungju (0.94), Anseong (0.93), and Icheon (0.92) are following in order after Jeju. Jeju is, therefore is following best practices by operating at maximum efficiency technically demonstrating a level of 100% efficiency. It means

Table 3 . CE, AE, TE of regional public hospitals in South Korea (2007-2010).

Table 4 .Scale efficiency of regional public hospitals in South Korea (2007-2010).
CEcrs, AEcrs, and TEcrs denote cost efficiency, allocative efficiency, and technical efficiency under CRS technology, respectively.
that there is no unnecessary input-mix in Jeju regional public hospital for a given level of output with the current technology. Half of the regional public hospitals indicate the comparatively high level of the technical efficiency while some hospitals still show more than 40% of high level of the technical inefficiency. It suggests that there is a potential to reduce their technical inefficiency via scaling input down or using optimal input mix since technical inefficiency is caused by using excess input mix or using improper input mix. In terms of the technical efficiency, Suncheon, Jinju, Uljin, and Gongju, and Daegu show much higher levels even though they show relatively low levels of cost efficiency. It indicates that these hospitals are much better at using input mix than implementing cost-saving input mixes because their technical efficiency indicates simply a capability to select the minimum input mix for a given level of output while the cost efficiency is a mix of allocative and technical efficiencies.
Overall, the cost efficiency over the 34 regional public hospitals shows quite a low level, compared to the allocative and technical efficiencies, and the technical efficiency is a bit higher than the allocative efficiency during the same time period. It shows that these hospitals are comparatively good at allocating the input mix and using suitable input mixes however they are not good at choosing the optimal cost obtainable from the existing technology. The reason why the cost efficiency is lower than other efficiencies might be explained by the fact that cost efficiency is measured by a combination of both allocative and technical efficiencies simultaneously, and it shows one (1.00) only if a production unit (here, a hospital) achieves at the level of 100% of technical as well as allocative efficiencies.
Scale efficiency (SE) expresses how close a regional public hospital is to the optimal scale: the larger SE, the closer the regional public hospital is to the optimal scale. The size of SE can be calculated by comparing the necessary input on the efficient VRS frontier and the necessary input on the CRS frontier. It indicates the likely gains from adjusting the hospital scale. Considering the scale efficiency would be appeal to the regional public hospital managers as well as policy makers since it gives a measure of what could be acquired by adjusting the size of each hospital. This might help the hospitals decide whether to choose an expansion or a contraction strategy. It might also help not only policy makers but also hospital managers understand the structural efficiency of the public medical sector.
The technical efficiency under CRS frontier (TECRS), the technical efficiency under VRS frontier (TEVRS), and the scale efficiency (SE) are shown in Table4 As seen in Table 4, most regional public hospitals do not operate under the optimum scale by showing that the TECRS, TEVRS, and SE of the whole regional public hospitals 0.74, 0.86, and 0.85, respectively. It implies that the technical inefficiency (26%) considering the CRS technology is different from that (14%) considering the VRS technology, and the former is higher than the latter, which eventually indicates that these hospitals do not operate at the optimum scale. It also implies that there is a possibility to save 15% of input mix if the hospitals produce their output with the optimum size.
When it comes to SE, Gangjin (0.62), Suncheon (0.61), Uljin (0.57), and Yeongwol (0.65) show the lowest level among 34 hospitals whereas Jeju shows the highest level (1.00). It represents that only Jeju operates at the optimum size while others do not. Also, it shows that Gangjin, Suncheon, Uljin, and Yeongwol might save 38%, 39%, 43%, and 35% of the input mix, respectively if they can operate at the optimal size.
In terms of the CRS technology (TECRS), Busan, Daegu, and Incheon in the metropolitan cities represent 0.66, 0.57, and 0.73, respectively, which are below the average level (0.74). It also means that these hospitals have a possibility to reduce 34%, 43%, and 27% of input set, respectively for a given level of output if they can operate at the optimal size. In terms of VRS technology (TEVRS), they still show 0.67, 0.67, and 0.75, respectively, which are lower than the average level (0.86). It means that there is a potential to save 33%, 33%, and 25% of the input set, respectively if they can operate at the optimal size. Finally, it indicates that these hospitals do not operate at the optimal scale by showing that the level of SE is less than one (1.00). Especially, SE (0.83) of Daegu is still below the average level (0.85). Whereas Gangjin, Jeju, Gangneung, Icheon, and Paju shows one (1.00) under the assumption of the VRS technology, which means they operate at the optimum scale. It suggests that these hospitals are technically efficient at the level of 100% in terms of utilizing the input set with increasing or decreasing returns to scale technology.
Overall, only Jeju is efficient under the CRS technology while some hospitals such as Gangjin, Gangneung, Icheon, Anseong, and Paju besides Jeju are efficient relative to VRS technology. Since Jeju is efficient relative to both CRS and VRS technologies, only it shows the optimal size of one (1.00). As mentioned above, this implies that almost all hospitals are lost from not having the high average product that one would have at the most productive scale since the scale efficiency measures the capability to operate where the average output bundle per input bundle is maximal.
4. Discussion and Conclusion
4.1. Discussion
The need for management improvement for the hospitals in South Korea has been a subject of recent debate. The budget deficit in public hospitals has grown worse due in part to the management performance of regional public hospitals. These hospitals have faced huge deficits from which they have been unable to recover. Moreover, many regional public hospitals have been faced with difficulties such as unpaid wages, old facilities, and the lack/shortage of medical workers along with the aforementioned accumulated deficits.
These hospitals are, however, required to provide medical services to the public including but not limited to the treatment of foreign workers, senior citizens, and low-income citizens. They must accomplish this despite the financial difficulties mentioned above. Considering the situation these hospitals have encountered, re
TEcrs, TEvrs, and SE denote technical efficiency under CRS technology, technical efficiency under VRS. technology, and scale efficiency, respectively.
sult-oriented economic performance, for hospitals, is an important matter, i.e., raising the level of efficiency. It can be a useful way to analyze the level of improvement of inefficiency in a time of limited resources.
Although the empirical results above show that there is the possibility of reducing inefficiency of by reallocating the input mix and scaling input back, it is hard to implement this due successfully due to the inherent financial weakness of these facilities due in part to a lack of high-quality human resources or decreasing financial support from the government. In terms of the public good, regional public hospitals have performed an important role in society, which private hospitals avoid due to the poor returns from running certain types of treatment such as departments of psychiatry or gynecology. However, when it comes to the financial status of these hospitals, especially those in municipalities who lack financial independence, these facilities are unable to pay the expenses of adding an extension to a building or remodeling infrastructure. Therefore, in order to facilitate their objectives the central government as well as local governments need to allow these hospitals to compensate for the losses resulting from their operating deficits by financially supporting them both actively and rationally. For this, it would be helpful to develop analytical tools reflecting the unique role of the regional public hospitals in a way that is separate from that of private hospitals. It is also important to analyze whether or not an individual regional public hospital hires the proper amount of input sets under the optimal scale. In this context, this paper may contribute by giving policy makers or hospital administrators useful information about their economic performance particularly with regard to regional public hospitals. Yet this study limited in its attempt to provide a comprehensive analysis of these hospitals. Future research may consider some important factors such as the quality of medical service, or case mix, which are important variables in the production process for hospitals.
4.2. Conclusions
This paper estimates the cost efficiency of 34 regional public hospitals in South Korea from 2007 to 2010 using DEA. Here are our findings from this analysis:
First of all, the cost efficiency, allocative efficiency, and technical efficiency of the whole regional public hospitals on average are 0.52, 0.71, and 0.74, respectively. It implies that although more than half of the hospitals are comparatively efficient allocatively and technically, they have not been good at selecting the cost-minimal input mix. In terms of the cost efficiency, as the average of the 34 regional public hospitals shows 0.52, there is 48% of the cost inefficiency during the same period. Hence, there is a possibility to improve its overall economic inefficiency from 15% to 67% given level of output by eliminating the factor of the cost inefficiency. Jeju (0.85) is ranked first, and Chungju (0.71), Seoul (0.70), Anseong (0.70), and Paju (0.70) are following in order after Jeju. It means that there is no regional public hospital, which fully achieves the overall cost minimization, and most of these hospitals are far away from the optimal cost obtainable from the existing technology.
Second of all, with respect to the allocative efficiency, Jeju (0.85) still shows the highest level of the efficiency, and Seoul holds second. Since the allocative efficiency for an individual hospital ranges from 0.57 to 0.85, it indicates that there is a potential to decrease its allocative inefficiency from 15% to 43% by reallocating the input mix. It also indicates that there is no regional public hospital, which completely reaches the goal of choosing input prices in order to minimize the cost, and most of the hospitals are allocatively inefficient for a given level of output and input prices.
Thirdly, when it comes to the technical efficiency, Jeju shows the maximum efficiency (1.00), and Paju (0.97), Chungju (0.94), Anseong (0.93), and Icheon (0.92) are following in order after Jeju. Thus, Jeju is a best practice in terms of the technical efficiency, and there is no unnecessary input mix in this regional public hospital for a given level of output with the current technology. Half of the regional public hospitals represent the comparatively high level of the technical efficiency while some hospitals still show more than 40% of high level of the technical inefficiency. It suggests that there is a potential for the technical efficiency improvement via scaling input down or using optimal input mix.
Finally, most regional public hospitals do not operate under the optimum scale by showing that the technical efficiency under CRS frontier, the technical efficiency under VRS frontier, and the scale efficiency of the whole regional public hospitals are 0.74, 0.86, and 0.85, respectively. It implies that the technical inefficiency considering the CRS technology is different from that considering the VRS technology, and the former is higher than the latter, which indicates that these hospitals do not operate at the optimum scale. It also implies that there is a possibility to save 15% of input set if the hospitals operate at the optimum size. Only Jeju shows the optimal scale of one (1.00) because it is efficient relative to both CRS and VRS technologies. It implies that almost all hospitals are lost from not having the high average product that one would have at the most productive scale size since the scale efficiency measures the capability to operate where the average output bundle per input bundle is maximal.
NOTES
1The Asian financial crisis is commonly referred to as the IMF crisis in South Korea, which was started in Thailand with the financial collapse of the Thai baht in July 1997, and most of the countries in East Asia were affected by the crisis. The effect of the IMF crisis has incurred the issue of the structural improvement of a society as a whole in South Korea.
2According to a report, The Actual Condition Survey of Regional Public Hospitals by Kim Mi-Hui (2012), based on year 2011, the accumulated deficit and the liability of these hospitals were 514 billion won and 172 billion won, respectively, which are mainly caused by relatively low financial independence.
3Health and medical care service from the regional public hospitals is to guarantee the public health benefit, especially for the poor and the underprivileged. The government intervention of this service is justified as the service is a sort of quasi-public good which causes externality and eventually results in market failure. This nature of health and medical care brings a trade-offs between equity and efficiency, or between publicness and profitability; the more these hospitals provide the service to the public, the more they pay, which is against economic efficiency.

4In general, economists choose medical revenue, number of patient treated, number of patient days, or case-mix as output of hospitals. Although we could not utilize the case-mix of the hospitals due to the lack of the accessibility of data, we used the adjusted number of patients instead, including in and outpatients, as output to reflect free medical treatment, for the economically and socially disadvantaged population as the public achievement for each regional public hospital since the number of patients contains the number of the beneficiaries of free medical treatment.

5The case when an increment in input is not able to reduce output is referred to strong disposability of input. Here, S stands for strong disposability of input.
6The figure is modified of “Input-Output Ferrell Decomposition” by F a
re and Grosskopf (2000), Reference Guide to OnFront2, pp.25.

7It indicates the variable returns to scale if the weighted density vector is equal to one (1).