An Asymptotic Distribution Function of the Three-Dimensional Shifted van der Corput Sequence ()
1. Introduction
In this paper we apply the Weyl’s limit relation [1] (p. 1-61)
 (1.1)
(1.1)
to the sequence , where
, where 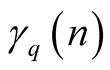 is the van der Corput sequence in base
is the van der Corput sequence in base  and
and  is the asymptotic distribution function (abbreviated a.d.f.) of
is the asymptotic distribution function (abbreviated a.d.f.) of  and
and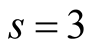 . The van der Corput sequence in base
. The van der Corput sequence in base  is defined as follows: Let
is defined as follows: Let  be the
be the  -adic expression of a positive integer
-adic expression of a positive integer . Then
. Then
 (1.2)
(1.2)
It is well-known that this sequence is uniformly distributed (abbreviated u.d.), see [1] (2.11, p. 2-102), [2] (Theorem 3.5, p. 127), [3] (p. 41).
For  a motivation for the study of the distribution function (abbreviated d.f.)
a motivation for the study of the distribution function (abbreviated d.f.) 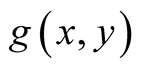 of
of
 ,
,  is a result of Pillichshammer and Steinerberger in [4] which states that
is a result of Pillichshammer and Steinerberger in [4] which states that
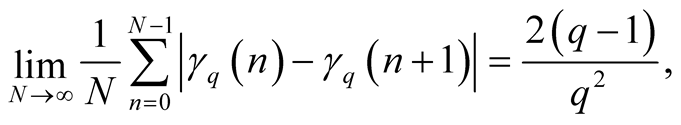 (1.3)
(1.3)
while in J. Fialová and O. Strauch [5] the relation (1.3) was proved applying (1.1) as

Moreover, in the Unsolved Problems [6] (1.12), the following problem is stated: Find the d.f. 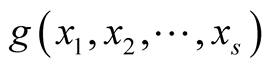 of the sequence
of the sequence ,
,  , in
, in . Ch. Aistleitner and M. Hofer [7] gave the following theoretical solution:
. Ch. Aistleitner and M. Hofer [7] gave the following theoretical solution:
Theorem 1 Let 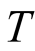 denote the von Neuman-Kakutani transformation described in Figure 1. Define the
denote the von Neuman-Kakutani transformation described in Figure 1. Define the  - dimensional curve
- dimensional curve , where
, where . Then the searched a.d.f. is
. Then the searched a.d.f. is

where  is the Lebesgue measure of a set
is the Lebesgue measure of a set .
.
The paper consists of the following parts: After definitions (Part 2) we derive the a.d.f. of 

Figure 1. Line segments containing 
 The graph of the von Neumann-Kakutani transformation
The graph of the von Neumann-Kakutani transformation .
.
Haoshangban (Part 3), the a.d.f. of  (Part 4), intervals containing
(Part 4), intervals containing  in diagonals (Part 5) and an explicit form of a.d.f.
in diagonals (Part 5) and an explicit form of a.d.f. 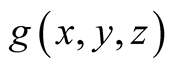 (Part 6). As an application (Part 7) we compute the limit
(Part 6). As an application (Part 7) we compute the limit
 (1.4)
(1.4)
for ,
,  and
and , respectively, see (0.39), (0.41) and (0.46).
, respectively, see (0.39), (0.41) and (0.46).
2. Definitions and Notations
Let ,
, 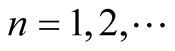 be a sequence in the unit interval
be a sequence in the unit interval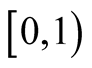 . Denote
. Denote


the step distribution function (step d.f.) of the finite sequence  in
in , while
, while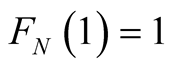 .
.
 A function
A function  is a distribution function (d.f.) if
is a distribution function (d.f.) if
(i)  is nondecreasing;
is nondecreasing;
(ii) 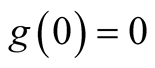 and
and .
.
 A d.f.
A d.f.  is a d.f. of the sequence
is a d.f. of the sequence ,
,  if an increasing sequence of positive integers
if an increasing sequence of positive integers 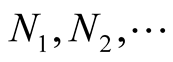 exists such that
exists such that  a.e. on
a.e. on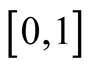 .
.
 A d.f.
A d.f. 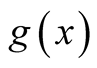 is an asymptotic d.f. (a.d.f.) of the sequence
is an asymptotic d.f. (a.d.f.) of the sequence ,
,  if
if  a.e. on
a.e. on .
.
 The sequence
The sequence 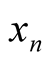 is uniformly distributed (abbreviating u.d.) if its a.d.f. is
is uniformly distributed (abbreviating u.d.) if its a.d.f. is .
.
 Similar definitions take place for
Similar definitions take place for  and
and  -dimensional sequence
-dimensional sequence ,
,  , in
, in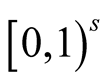 , cf. [1] (1.11, pp. 1-60).
, cf. [1] (1.11, pp. 1-60).
 In the sequel the
In the sequel the  -dimensional interval
-dimensional interval  we denote by
we denote by , where
, where  are projections on
are projections on  axes, respectively.
axes, respectively.
3. a.d.f. of 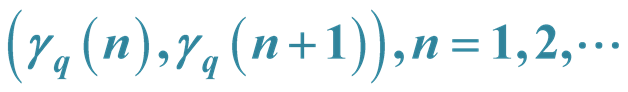
Let  be an integer.
be an integer.
Lemma 1 Every point ,
, 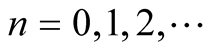 , lies on the diagonals of intervals
, lies on the diagonals of intervals
 (1.5)
(1.5)
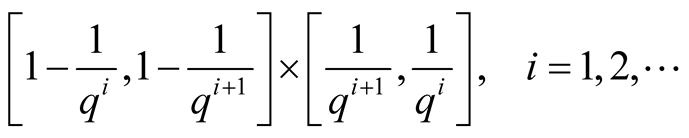 (1.6)
(1.6)
Proof. Express an integer  in the base
in the base 
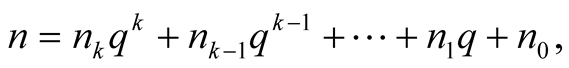
where  and
and . We consider the following two cases:
. We consider the following two cases:
 ,
,
 .
.
Let
 Then
Then
 ,
,
 and by (0.2)
and by (0.2)
 . In this case
. In this case

Thus such  lies on the line-segment
lies on the line-segment
 (1.7)
(1.7)
Let
 Then
Then
 and
and , where
, where . Then
. Then
 . Thus
. Thus
 ,
,
 , and we have
, and we have
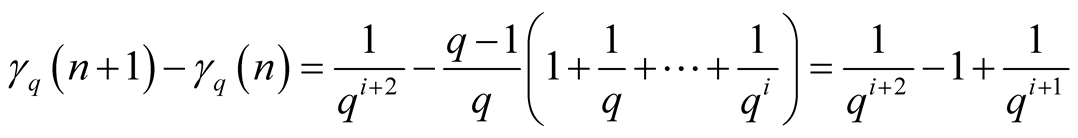 and
and
 and
and
 . Thus such
. Thus such  lies on the segment
lies on the segment
 (1.8)
(1.8)
Thus, for , terms of the sequence
, terms of the sequence 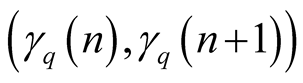 lie on the diagonal of the interval
lie on the diagonal of the interval
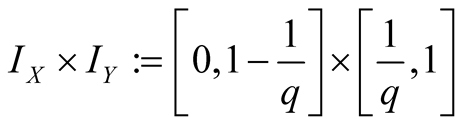 (1.9)
(1.9)
and for , after reduction
, after reduction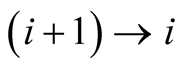 , terms of the sequence
, terms of the sequence  lie on the diagonals of the intervals
lie on the diagonals of the intervals
 (1.10)
(1.10)
These intervals are maximal with respect to inclusion.
Adding the maps (1.7) and (1.8) we found the so-called von Neumann-Kakutani transformation , see Figure 1. Because
, see Figure 1. Because 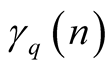 is u.d., the sequence
is u.d., the sequence 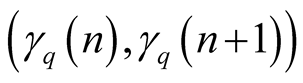 has a.d.f.
has a.d.f.  of the form1
of the form1
 (1.11)
(1.11)
where  is the projection of a two dimensional set to the
is the projection of a two dimensional set to the  -axis.
-axis.
The sum (1.11) implies
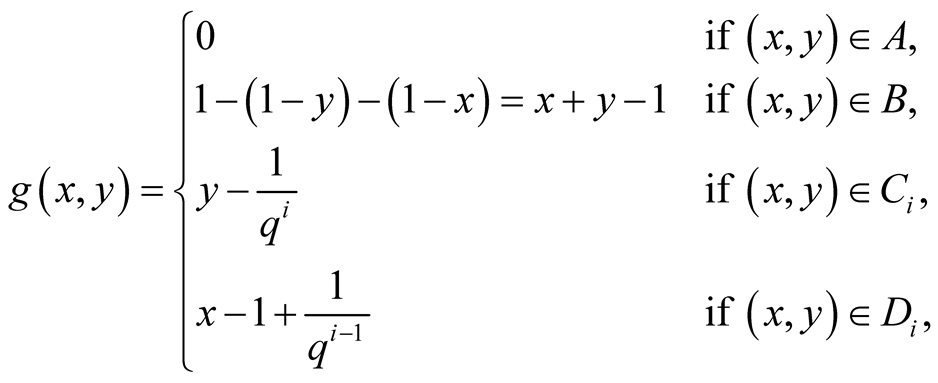 (1.12)
(1.12)

From (1.12) it follows
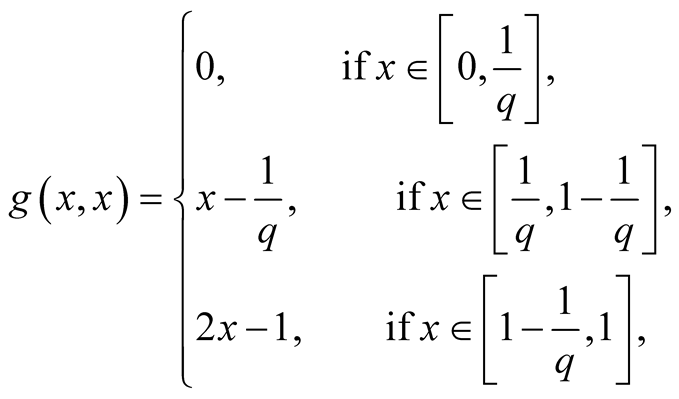 (1.13)
(1.13)
and for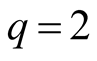 , the mean equality misses.
, the mean equality misses.
4. a.d.f. of 
Let  be an integer.
be an integer.
Lemma 2 All terms of the sequence ,
, 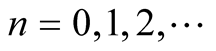 , lie in the diagonals of the following intervals
, lie in the diagonals of the following intervals
 (1.14)
(1.14)
 (1.15)
(1.15)
 (1.16)
(1.16)
Proof. Express an integer  in the base
in the base 
 (1.17)
(1.17)
where 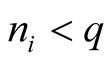 and
and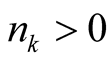 . We consider three following cases:
. We consider three following cases:
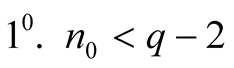 ,
,
 ,
,
 .
.
Let
 Then
Then
 ,
,
 and
and
 . In this case
. In this case
 and thus such
and thus such 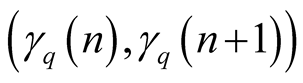 lies on the line-segment
lies on the line-segment
 (1.18)
(1.18)
Let
 . Then
. Then
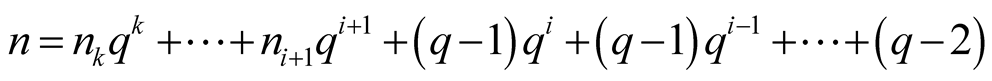 and
and , then
, then
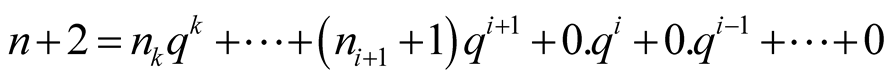 . Thus
. Thus
 ,
,
 , and we have
, and we have
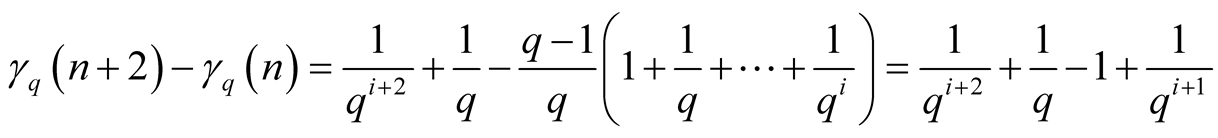 .
.
Furthermore
 and
and
 .
.
Thus in this case  lies on the line-segment
lies on the line-segment
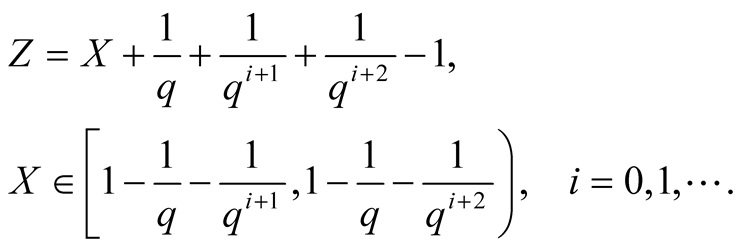 (1.19)
(1.19)
Let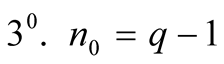 .
.
Then
 and
and , then
, then
 . Thus
. Thus
 ,
,
 , and we have
, and we have
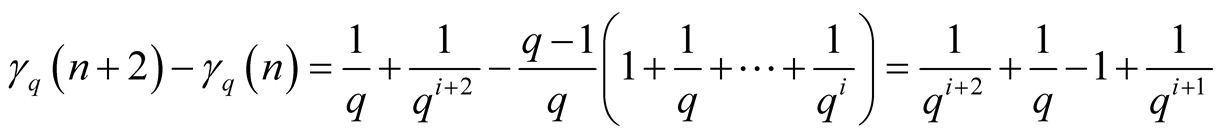 .
.
Furthermore
 and
and
 .
.
This gives
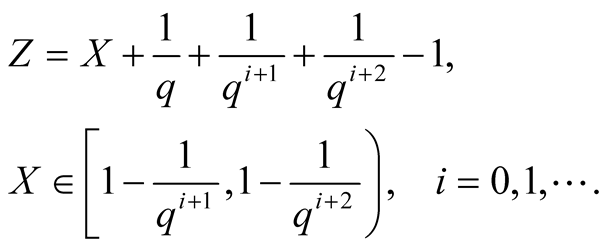 (1.20)
(1.20)
Summary, if the  satisfies
satisfies , then
, then  is contained in the diagonal of
is contained in the diagonal of
 (1.14)
(1.14)
for  in the diagonal of
in the diagonal of
 (1.15)
(1.15)
and for  in the diagonal of
in the diagonal of
 (1.16).
(1.16).
Proof. Express an integer  in the base
in the base 
 (1.17)
(1.17)
where 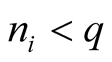 and
and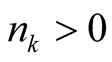 . We consider three following cases:
. We consider three following cases:
 ,
,  ,
, .
.
Let
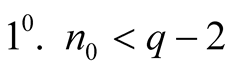 Then
Then ,
, 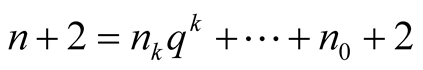 and
and . In this case
. In this case
 and thus such
and thus such  lies on the linesegment
lies on the linesegment
 (1.18)
(1.18)
Let
 . Then
. Then  and
and , then
, then
 . Thus
. Thus ,
,
 , and we have
, and we have
 .
.
Furthermore
 and
and .
.
Thus in this case  lies on the line-segment
lies on the line-segment
 (1.19)
(1.19)
Let
 . then
. then 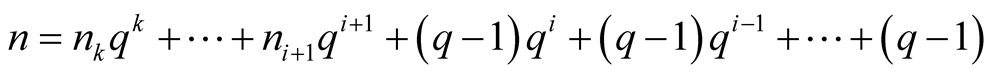 and
and , then
, then
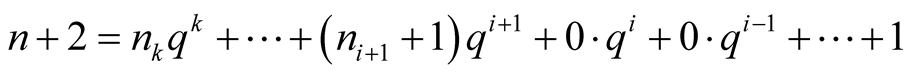 . Thus
. Thus
 ,
,
 , and we have
, and we have  .
.
Furthermore
 and
and .
.
This gives
 (1.20)
(1.20)
Summary, if the  satisfies
satisfies , then
, then  is contained in the diagonal of
is contained in the diagonal of
 (1.14) for
(1.14) for  in the diagonal of
in the diagonal of
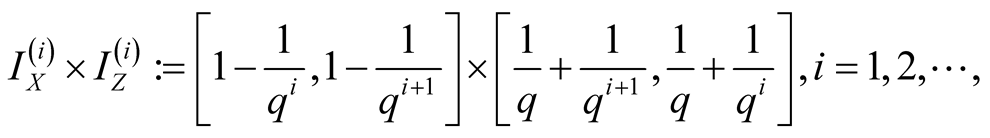 (1.15)
(1.15)
and for  in the diagonal of
in the diagonal of
 (1.16).
(1.16).
Composition of the maps (0.18), (0.19) and (0.20) of  forms the second iteration
forms the second iteration  of the von Neumann-Kakutani transformation
of the von Neumann-Kakutani transformation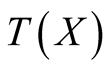 . The diagonals of (1.14), (1.16) and (1.15) yield the following graph of
. The diagonals of (1.14), (1.16) and (1.15) yield the following graph of  in Figure 2.
in Figure 2.
Here the interval 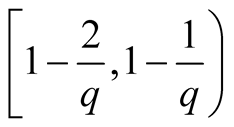 on
on  -axis is decomposed in
-axis is decomposed in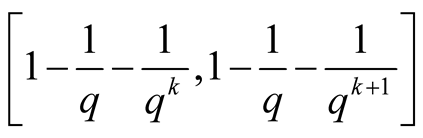 ,
,  , and the interval
, and the interval  is decomposed in
is decomposed in ,
, . On
. On  -axis the interval
-axis the interval  is decomposed in
is decomposed in ,
,  and the interval
and the interval 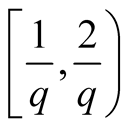 is decomposed in
is decomposed in ,
, . Note that for
. Note that for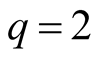 , the interval
, the interval 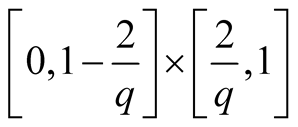 has a zero length and is missing.
has a zero length and is missing.
Exchange for a moment the axis  by
by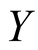 . Similarly as in (1.11), we have that the a.d.f.
. Similarly as in (1.11), we have that the a.d.f.  of the sequence
of the sequence  is
is
 (1.21)
(1.21)
Decompose  as the following figure shows:
as the following figure shows:
Then by Figure 3 we have

Figure 3. Decomposition of the Vunit square to parts with fixed expression of .
.
 (1.22)
(1.22)
Let .
.
In this case we find a.d.f 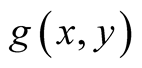 from (1.22) omitting
from (1.22) omitting 
In Part 7. Applications we need to find  from
from  in (1.22):
in (1.22):
For 
 (1.23)
(1.23)
For 
 (1.24)
(1.24)
For 
 (1.25)
(1.25)
Note that for  the term
the term  is omitted.
is omitted.
5. a.d.f. of 
Let  be an integer.
be an integer.
Lemma 3 Every point  is contained in diagonals of the intervals
is contained in diagonals of the intervals
 (1.26)
(1.26)
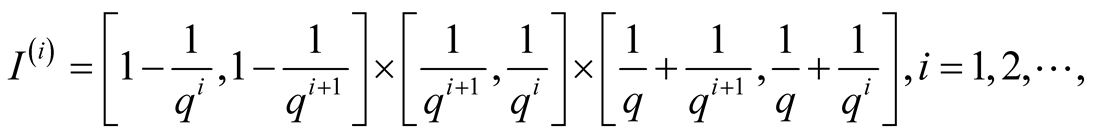 (1.27)
(1.27)

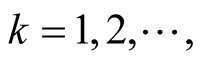 (1.28)
(1.28)
where  if
if . These intervals are maximal with respect to inclusion.
. These intervals are maximal with respect to inclusion.
Proof. Every maximal  -dimensional interval
-dimensional interval  containing points
containing points  will be written as
will be written as , where
, where  are projections of
are projections of  to the
to the , axes, respectively. Moreover if
, axes, respectively. Moreover if  then
then  and
and . From u.d. of
. From u.d. of  follows that the lengths
follows that the lengths . Combining intervals (1.5), (1.14), (1.15), (1.16), (1.6) of equal lengths by following Figure 3.
. Combining intervals (1.5), (1.14), (1.15), (1.16), (1.6) of equal lengths by following Figure 3.
We find (1.26), (1.27), and (1.28).
Now, let  be the union of diagonals of (1.27), (1.28) and (1.26). Again, as in (1.11), the a.d.f.
be the union of diagonals of (1.27), (1.28) and (1.26). Again, as in (1.11), the a.d.f.  has2 the form
has2 the form
 (1.29)
(1.29)
and it can be rewritten as
 (1.30)
(1.30)
To calculate minimums in (1.30) we can use the following Figure 4 (here ):
):
As an example of application of (1.30) and Figure 4, we compute  for
for  without using the knowledge of
without using the knowledge of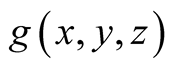 ,3
,3
 (1.31)
(1.31)
Proof.
1. Let .
.
Then ,
, 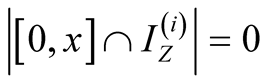 ,
, 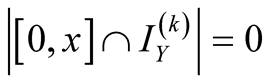 , consequently
, consequently .
.
2. Let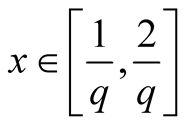 . Then
. Then ,
, 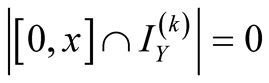 ,
,  , consequently
, consequently .
.
3. Let . Then
. Then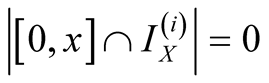 ,
,  , consequently
, consequently .
.
4. Let .
.
Specify ,
, . Then
. Then ,
,  for
for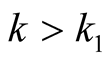 . Thus (1.30) implies
. Thus (1.30) implies

For  we have
we have
 (1.32)
(1.32)
6. Explicit Form of 
Let  be an integer.
be an integer.
Motivated by the Figure 4 we decompose the unit interval  on
on ,
,  and
and  axes in the Figure 5
axes in the Figure 5

Figure 4. Projections of intervals  on axes
on axes .
.

Figure 5. Divisions of the unit intervals.
intervals (here ):
):
In this decomposition, for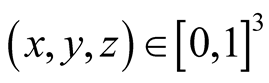 , we have
, we have  possibilities. We shall order choices of
possibilities. We shall order choices of  from the left to the right. Detailed proofs are included only in non-trivial cases.
from the left to the right. Detailed proofs are included only in non-trivial cases.
1. Let
 . Then
. Then
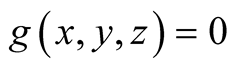 .
.
Proof. We have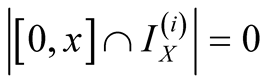 ,
,  ,
,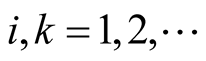 . Then, by (1.30),
. Then, by (1.30), .
.
Similarly, in the following cases 2-9.
2. Let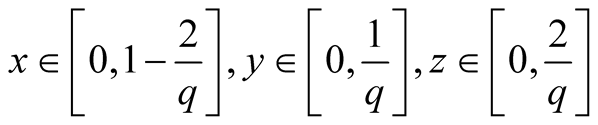 . Then
. Then
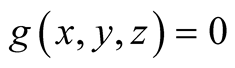 .
.
3. Let . Then
. Then
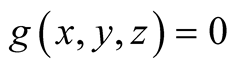 .
.
4. Let . Then
. Then
 .
.
5. Let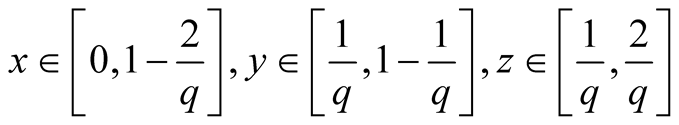 . Then
. Then
 .
.
6. Let . Then
. Then
 .
.
7. Let . Then
. Then
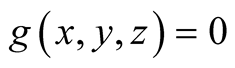 .
.
8. Let . Then
. Then
 .
.
9. Let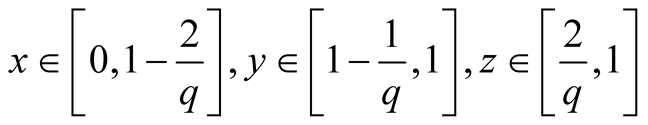 . Then
. Then
 .
.
Proof. We use .
.
10. Let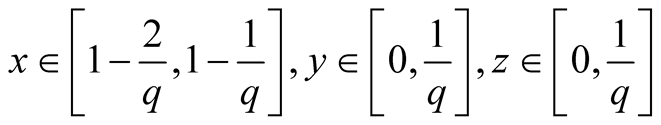 . Then
. Then
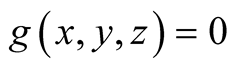 .
.
Proof. We use ,
,  ,
, . Similarly11. Let
. Similarly11. Let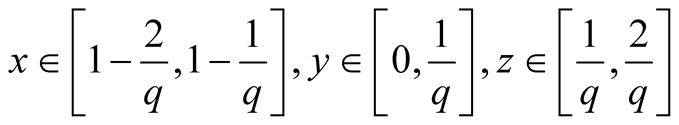 . Then
. Then
 .
.
12. Let . Then
. Then
 .
.
Proof. We use ,
, 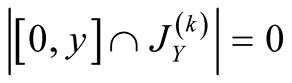 ,
, .
.
13. Let . Then
. Then
 .
.
14. Let . Then
. Then
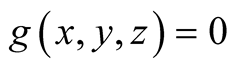 .
.
15. Let . Then
. Then
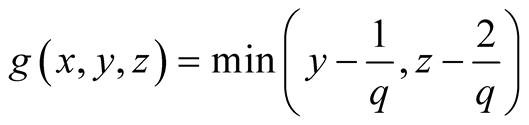 .
.
16. Let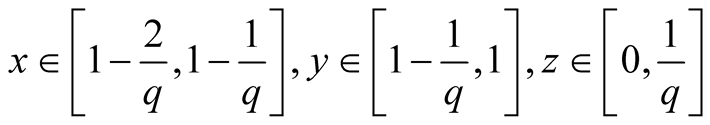 .
.
Specify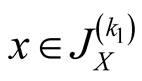 ,
, 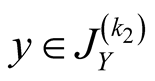 ,
, . Then
. Then

Proof. First observe that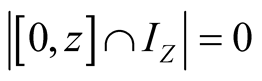 , and
, and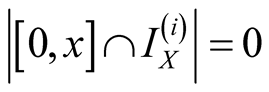 . Thus
. Thus
 and
and 
Further, for , we have
, we have



Thus, using (1.30), we find
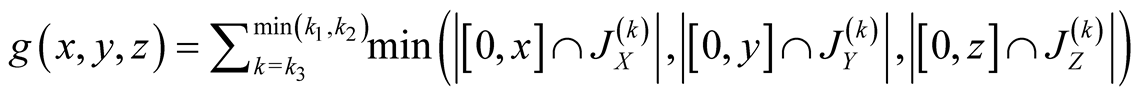 .
.
17. Let .
.
Specify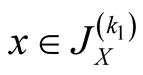 ,
, . Then
. Then

Proof. We have ,
, 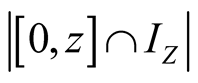 ,
, 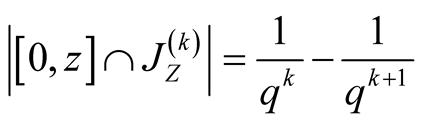 , then
, then

18. Let .
.
Specify ,
, . Then
. Then

Proof. We have

19. Let . Then
. Then
 .
.
20. Let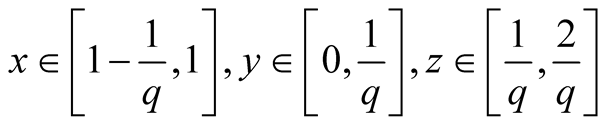 .
.
Specify ,
,  ,
, . Then we have
. Then we have

Proof. We have ,
,  and
and 
21. Let .
.
Specify ,
, . Then
. Then

Proof. ,
, 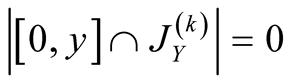 ,
,  ,
, 
22. Let . Then
. Then
 .
.
23. Let .
.
Specify ,
, . Then
. Then
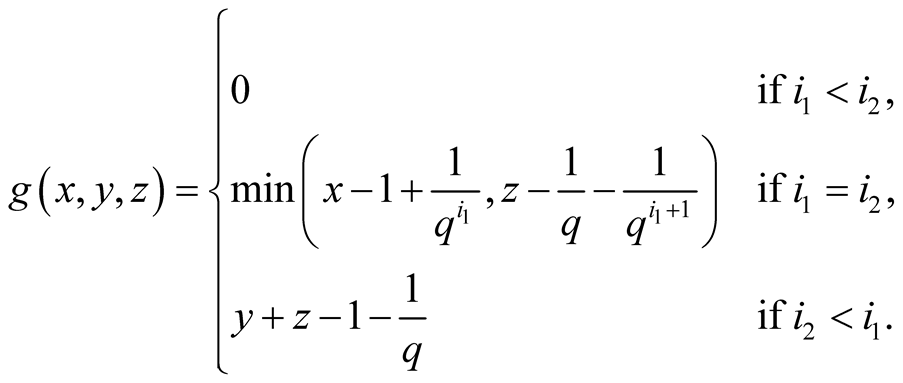
Proof. ,
,  ,
,  ,
, 
24. Let . Then
. Then
 .
.
Proof. We have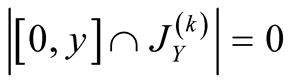 . Specify
. Specify . Then
. Then

The first term is 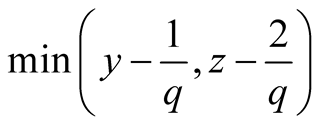 and the second is
and the second is .
.
25. Let .
.
Specify ,
, . Then
. Then

Proof.
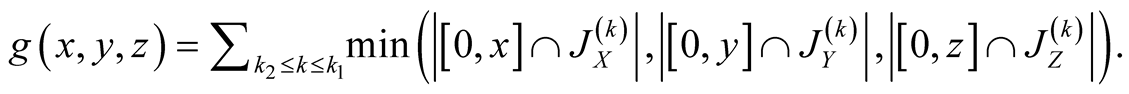
26. Let .
.
Specify ,
,  and
and . Then
. Then

Proof. We have ,
,  ,
,  ,
, . Moreover
. Moreover



which gives
 .
.
The final equation holds if  and
and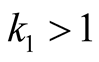 . It can be seen that it holds also for
. It can be seen that it holds also for 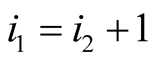 and
and . For
. For 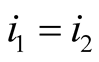 and
and  we need to compute this sum separately.
we need to compute this sum separately.
27. Let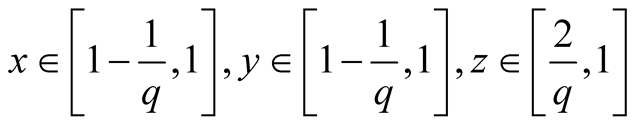 . Then
. Then
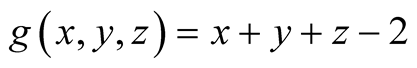 .
.
Proof. First observe
 ,
,  ,
,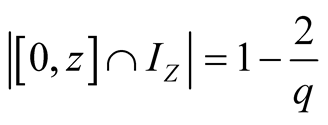 . Thus
. Thus
 .
.
New specify  and
and . Then we have
. Then we have


and ,
,  ,
, . Then for the sums in (1.30) we have
. Then for the sums in (1.30) we have

which gives .
.
The above computation of  holds for
holds for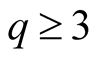 .
.
Let .
.
We have  and
and
 (1.33)
(1.33)
Thus  for
for  directly follows from
directly follows from 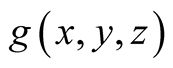 for
for 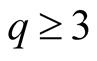 if we use only such items in
if we use only such items in  for which
for which ,
,  ,
, . These are
. These are , i.e.,
, i.e.,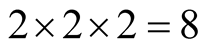 .
.
The non-zero values of 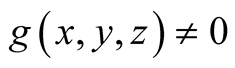 can also be seen in the following table.
can also be seen in the following table.
In all other cases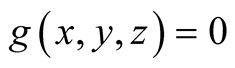 .
.
7. Applications
The knowledge of the a.d.f.  of the sequence
of the sequence 
 allows us to compute the following limit by the Weyl limit relation (1.1) in dimension
allows us to compute the following limit by the Weyl limit relation (1.1) in dimension .
.
 (1.34)
(1.34)
where 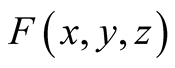 is an arbitrary continuous function defined in
is an arbitrary continuous function defined in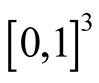 . For computing (1.34) we use the following two methods.
. For computing (1.34) we use the following two methods.
7.1. Method I
In the first method in the Riemann-Stieltjes integral (1.34) we apply integration by parts.
Lemma 4 Assume that 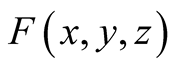 is a continuous in
is a continuous in  and
and  is a.d.f. Then
is a.d.f. Then
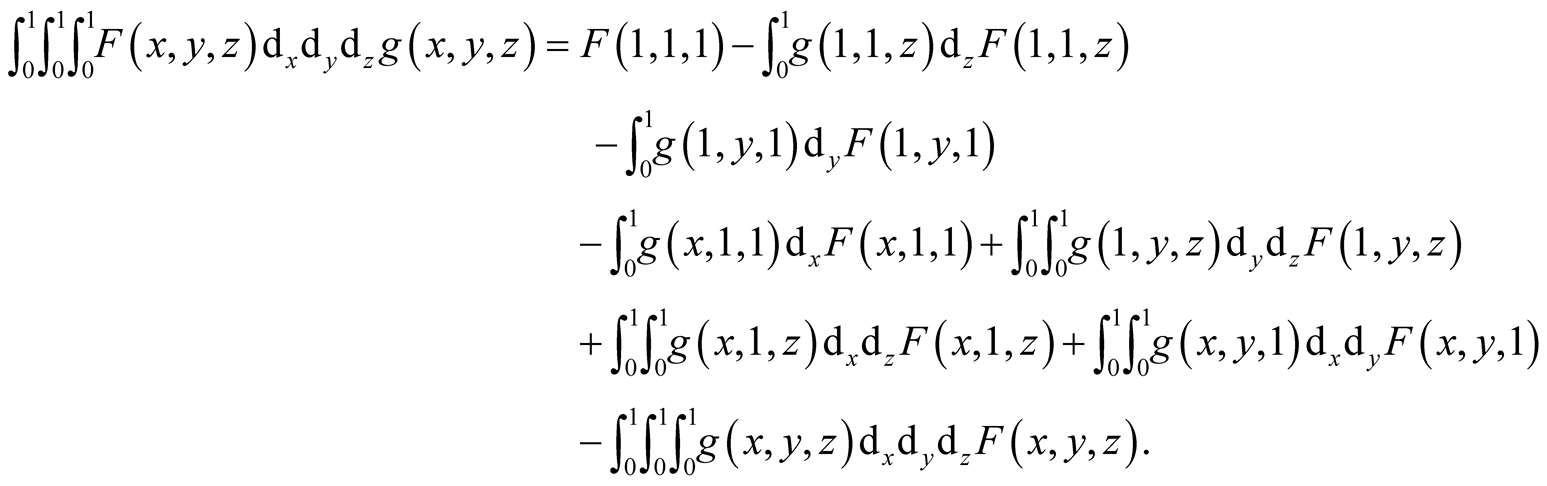 (1.35)
(1.35)
Here
 (1.36)
(1.36)
Note that


if the partial derivatives exist.
Exercise 1 Put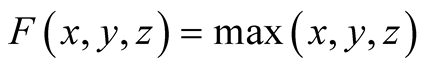 . We have
. We have
 ,
,
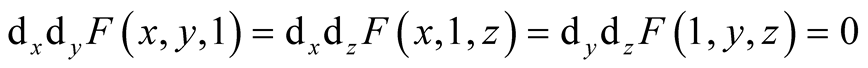 The differential
The differential  is non-zero if and only if
is non-zero if and only if  and in this case
and in this case .
.
Proof: For every interval  and every continuous
and every continuous  the differential
the differential  is defined as
is defined as
 (1.37)
(1.37)
Putting ,
,  ,
,  we have
we have

Then by (1.35)
 (1.38)
(1.38)
For 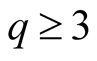 and by (1.31) we have
and by (1.31) we have

For  and by (1.32) we have
and by (1.32) we have

Therefore for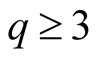 , by (1.34) and by (1.38) we have
, by (1.34) and by (1.38) we have
 (1.39)
(1.39)
Note that the same result follows from (1.44).
Exercise 2 Put . Since
. Since
 ,
,  if
if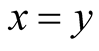 ,
,  if
if ,
,  if
if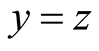 , and
, and  if
if  and
and  otherwiseapplying (1.34) and (1.35) we have
otherwiseapplying (1.34) and (1.35) we have
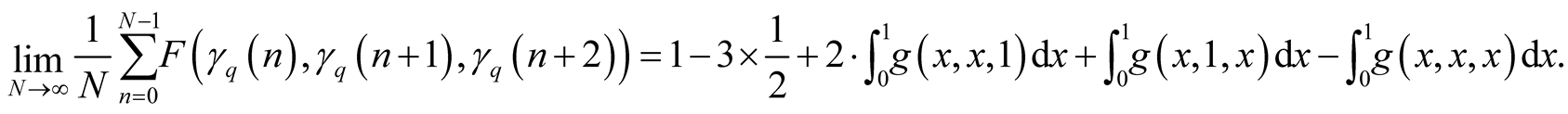 (1.40)
(1.40)
Here we have  in (1.13) for
in (1.13) for . For
. For  we use
we use 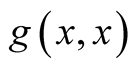 in (1.23) if
in (1.23) if , (1.24) if
, (1.24) if  and (1.25) if
and (1.25) if  and for
and for  we use (1.31) if
we use (1.31) if  and (1.32) if
and (1.32) if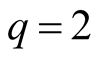 . Thus we have:
. Thus we have:
a) 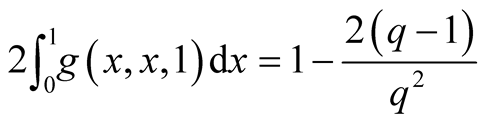 for
for ;
;
b)  for
for ;
;
c)  for
for ;
;
d)  for
for .
.
e)  for
for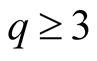 ;
;
f)  for
for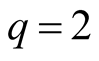 .
.
Putting a)-f) into (1.40) yields
 (1.41)
(1.41)
7.2. Method II
In the second method we compute the differential  directly. It is nonzero only for
directly. It is nonzero only for
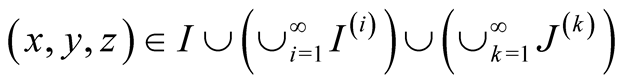 . For such
. For such 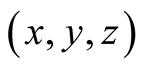 the a.d.f.
the a.d.f.  has the form
has the form
 (1.42)
(1.42)
Thus  and moreover
and moreover 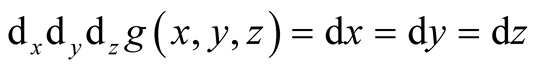 only on the following straight lines
only on the following straight lines



Considering three possible cases, calculate
 (1.43)
(1.43)
Summary
 (1.44)
(1.44)
Exercise 3 Put . By Method I, we have
. By Method I, we have , similarly
, similarly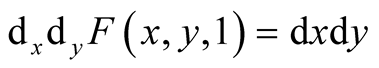 , etc., and by (1.35) we have
, etc., and by (1.35) we have
 (1.45)
(1.45)
Since a computation of (1.45) is complicated we use Method II, by (1.44) we have

Inserting these formulas into (1.44) we have
 (1.46)
(1.46)
for .
.
8. Conclusion
The problems solved in this paper is significantly more complicated in higher dimensions . For example, in dimension
. For example, in dimension , to compute the d.f.
, to compute the d.f. 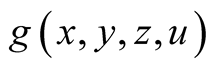 of the sequence
of the sequence , it is necessary to investigate
, it is necessary to investigate  cases analogous to
cases analogous to  cases for the explicit form
cases for the explicit form  in the part 0.6. Also Figure 3 would have to be converted to the dimension
in the part 0.6. Also Figure 3 would have to be converted to the dimension . Finally, we would need the third iteration of von Neumann-Kakutani transformation.
. Finally, we would need the third iteration of von Neumann-Kakutani transformation.
Acknowledgements
The paper is sponsored by the project P201/12/2351 of GA Czech Republic.
NOTES
1 is a copula.
is a copula.