Research on Location-Routing Problem with Empirical Analysis for Regional Logistics Distribution ()
1. Introduction
The concept of integrated logistic system has emerged as a new management philosophy with aims to increase distribution efficiency recently. All companies that aim to be competitive on the market have to pay attention to their organization related to the entire supply chain. In particular, companies have to increase the efficiency of their logistic operation. It is essential that a reasonable optimized system of logistics distribution for enterprises with the development of e-commerce and integrated logistics. Due to its complexity, it is model and solution of algorithm that core for LRP, which is NP-hard. The main contribution of this paper is the statement of two kinds of mathematical models for all the introduced problems, together with a proof of their correctness. Some methods for multi-objective location-routing problems (MLRP) are discussed on the modeling and solving. Multiobjective genetic algorithm (MGA) has been produced a technique to deal with multi-objective optimization problems. The methods are viewed as solving MLRP based on MGA. The specific methods for MLRP are presented by two-objective of LRP system. It has been proved that MGA provides a path for large-scale MLRP in integrated logistics. The research is under development, and it will be the subject of a future work.
The paper is organized as follows: Section 2 introduces the meanings and the complexity solution of MLRP. Section 3 describes the mathematical models of MLRP. Section 4 emphasizes on the solutions of MLRP. Section 5 shows the optimal models and solutions for two-objective LRP. Finally, the last section gives practical analysis based on random and conclusions and future work.
2. The Meanings and the Complexity Solution of MLRP
2.1. Basically Meanings of LRP
Cooper (1972) firstly generalized the transportation-location problem which aimed to find the optimal-location of supply sources and to minimize the transportation cost from such sources to destinations [1] . Watson-Gandy and Dohrn (1973) may be one of the first authors credited to consider the multiple-drop nature of the vehicle routes within the location-transportation framework [2] . Such popularity of LRP studies almost parallels the advent of an integrated logistics concept and the growth of international trade, which necessitated distribution efficiency. Golden and Backer (1985) observed that the multi-objective context is a rule rather than an exception in both private and public sector logistics operations [3] . For example, the minimum cost route, primarily based on the spatial dispersion of customer nodes, may fail to meet customers ’needs for on-time delivery services. Accordingly, most real-world location-routing problems are characterized by more than one conflicting objectives. Early LRP articles have recognized the multi-objective nature, they mainly focused on finding the origin-destination path rather than solving node-covering problems that required complete Hamiltonian tours. There is a fixed cost associated with opening a facility at each potential site, and a distribution cost associated with any routing of vehicles that includes the cost of acquiring the vehicles used in the routing, and the cost of delivery operations. The cost of delivery operations is linear in the total distance traveled by the vehicles. In generally, the objective function of LRP minimizes the total cost of routing and acquisition of the vehicles, and locating and operating the depots. Sometimes other objectives are considered such as transportation just in time, satisfying the specific needs of customers or maximum total profits. In a word, there are many objectives in LRP, which are existed in different conflicts [4] .
2.2. The Complexity Solution of MLRP
LRP considers tours and then seeks the optimal facility location and route design simultaneously so that it can interrelate those two decisions, that is to say, LRP consists two processes of location-allocation (LA) and vehicle routing problem (VRP), which is complex rather than the two others. For the conflicts of different objectives in LRP, the design is determined by minim cost, which is violated the required time of customers. But LRP belongs to NP-hard, it is model and solution of algorithm that core for LRP. Two distinct types of solution methods have been used for solving LRP. These are exact algorithms and heuristics. Exact algorithms have been limited to small and medium size instances (up to 20 - 50 customers). As the problem size gets larger, heuristic procedures prove to be the only viable alternative. The researches of LRP focus on multi-objectives optimization because of the characteristics of multi-objective in real logistic systems. So there existed in complexities of LRP optimization in integrated logistics.
3. Mathematical Models of MLRP
3.1. The Optimal Model of Common Problem in Multi-Objective Engineering System
Generally, the models [5] of engineering systems reliability are expressed by:
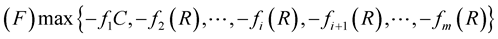 (1)
(1)
where 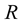 is a function of continuous increasing,
is a function of continuous increasing,
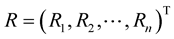 ,
, 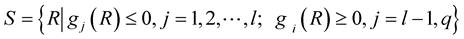 ,
,
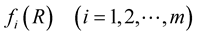 ,
,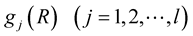 .
.
3.2. Several Models of MLRP
3.2.1. The Description with Classical Optimization of MLRP
Let 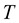 represents the numbers of objectives in MLRP by
represents the numbers of objectives in MLRP by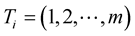 . The method is unified to minimize the values of all objectives.
. The method is unified to minimize the values of all objectives.
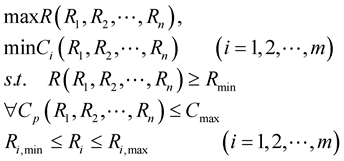 (2)
(2)
where  is reliability that is function of the reliability in each unit of LRP by
is reliability that is function of the reliability in each unit of LRP by . These values are determined by the constraints of their low limit.
. These values are determined by the constraints of their low limit.  represents system cost that is also function of each unit.
represents system cost that is also function of each unit. 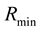 is the low-limit value with constraint of the system.
is the low-limit value with constraint of the system. 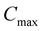 is the high-limit value with constraint of it.
is the high-limit value with constraint of it. 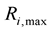 and
and 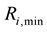 are separately the high-low limit of the unit reliability, which can be chosen “1” or “0” if the values aren’t given in practical LRP.
are separately the high-low limit of the unit reliability, which can be chosen “1” or “0” if the values aren’t given in practical LRP.
3.2.2. The Weight Expression for MLRP
The most intuitive approach to deal with multiple objectives would be to combine them into a single function. The approach of combining objectives into a single (scalar) function is normally denominated aggregating functions, and it has been attempted several times in the literature with relative success in problems in which the behavior of the objective functions more or less well known [6] . An example of this approach is a sum of weights of the form:
 (3)
(3)
where 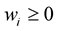 are the weighting coefficients representing the relative importance of the
are the weighting coefficients representing the relative importance of the  objective functions of the problem. It is usually assumed that
objective functions of the problem. It is usually assumed that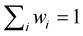 .
.
4. Solution Methods for MLRP
4.1. General Algorithms for Multi-Objective Optimal Problems
In general, the methods for multi-objective optimization problems are compound of an approach combined them into a single function and then solving the single objective one, nonlinear programming and heuristic [7] .
4.2. Solving Methods to MLRP
4.2.1. The Method Combined Multicriteria Optimization into a Single Optimization
Assume that the two objective functions are to be minimized. For obtaining satisfactory solution of LRP, the optimal models combined multicriteria optimization into a single one are proposed, which introduces a global satisfaction function integrated two single objective functions. The small operator “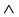 ” and weight sum index are carried so as to combine the different single satisfactory function in the model (1) of part 3.1. The global satisfaction function is given by:
” and weight sum index are carried so as to combine the different single satisfactory function in the model (1) of part 3.1. The global satisfaction function is given by:
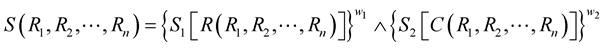 (4)
(4)
where 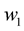 and
and  are denoted by satisfactory indexes of reliability. And cost is stated with different values of two objectives. The values with weight sum indexes are considered by period [0, 1], which “1” represents the most value, while “0” is the unimportant one. In a word, it is obtainable that multicriteria optimization transformed into a single one. Then the nonlinear programming is used for the single optimization [8] .
are denoted by satisfactory indexes of reliability. And cost is stated with different values of two objectives. The values with weight sum indexes are considered by period [0, 1], which “1” represents the most value, while “0” is the unimportant one. In a word, it is obtainable that multicriteria optimization transformed into a single one. Then the nonlinear programming is used for the single optimization [8] .
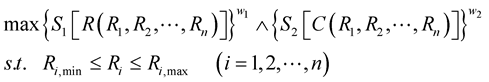 (5)
(5)
4.2.2. Multi-Objective Genetic Algorithm (MGA) Based on Pareto for LRP
The core of MGA: The key points are involved in MGA (MGA optimization technique exist in the key points):
1) How to scale and choose the fitness.
2) How to maintain the diversity of the population.
It is a widely used method for decider that MGA based on Pareto. And it is an optimization technique with decision before searching.
5. Empirical Analysis
In this paragraphy the practical analysis is presented for regional logistics distribution as Fujian Province as example [9] . Firstly, the geographic map is given in Funjian Province. There are nine cities including Xiamen, Quanzhou, Putian, Fuzhou, Ningde, Nanping, Sanming, Longyan and Zhangzhou, which are chosen the distribution node. The random model is proposed with these nine cities. The Markov Chain is proposed for these cities. The map is given in Figure 1. This chain is applied to processes with regional distribution level in Figure 2. The set 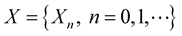 in which a process takes its values is called its state space, which refer to the node that distribution vehicle is A. Markov chain on a finite or countably infinite state space
in which a process takes its values is called its state space, which refer to the node that distribution vehicle is A. Markov chain on a finite or countably infinite state space 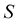 is a family of
is a family of 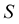 - value random variables
- value random variables 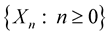 with the property that, for all
with the property that, for all 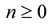 and
and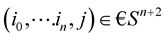 .
.
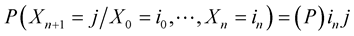 , where
, where 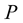 is a matrix all of whose enties are negative and each of whose rows sums to (9). Equivalently
is a matrix all of whose enties are negative and each of whose rows sums to (9). Equivalently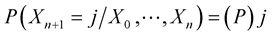 .
.
 (6)
(6)
Equivalently
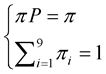 (7)
(7)
for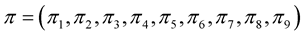 , Then
, Then
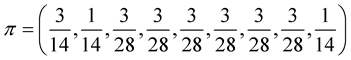 .
.
If 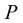 is a one-step transition matrix.
is a one-step transition matrix. 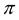 obey the steady state distribution and a corresponding characteristic root which is equal to one, the transfer matrix eigenvectors. The normal situation is considered for regional distribtion with trucks. Different cities have different probabilities for the trucks. The probability give further distribution reference for design these city agent. Then the logistics coordination is given based multi-agent for optimization.
obey the steady state distribution and a corresponding characteristic root which is equal to one, the transfer matrix eigenvectors. The normal situation is considered for regional distribtion with trucks. Different cities have different probabilities for the trucks. The probability give further distribution reference for design these city agent. Then the logistics coordination is given based multi-agent for optimization.
The conclusion is given that the stayed probability is contained for long-time. And the distribution vehicle will be stayed with state rate. And the different rate is obtained by the different cities. The lower-level coordinate is the
○—city; ① Xiamen; ② Quanzhou; ③ Putian; ④ Fuzhou; ⑤ Ningde; ⑥ Nanping; ⑦ Sanming; ⑧ Longyan; ⑨ Zhangzhou.
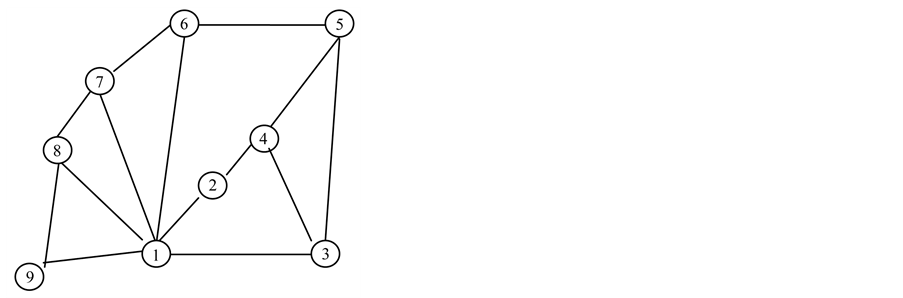
Figure 2. Nine cities position in Fujian.
co-ordination between companies agent with similar enterprise agent; the middle-level agent is the co-ordinate between city agents with enterprise agent; the high-level coordinate is the co-ordination between city agents with similar city agent. Logistics coordinate levels proposed in Figure 3.
6. Conclusion
The complexity in optimization model and solution are briefly discussed for logistics distribution network in the paper. For each scenario, two kinds of mathematical programming formulations have been proposed. In particular, these formulations will be used as a mathematical basis to design solution methods, both exact algorithm and heuristic. The paper focuses on three methods for MLRP, especially MGA based on Pareto. All these methods provide a path for solving large-scale MLRP in integrated logistics. The application to other combinatorial optimization problems should be investigated in integrated logistics. The practical random analysis is given a path for regional distribution [7] [8] .
Acknowledgements
This paper was supported in part by Program for New Century Excellent Talents in University under grant number NCET-10-0118, in part by 2013 year Ministry of Culture art of Scientific Research Project under grant number 13DH50, in part by National Natural Science Foundation of China under grant number 71040009.