Josephson Fourier Spectrometer Based on HTSP: Construction and Quantum Computer Realization Problem ()
1. Introduction: Non-Stationary Josephson Effect in HTSC Systems and Its Applications
Previously we have investigated non-stationary Josephson effect via dot junction, which was performed by crossing of edges of two prisms of Y1Ba2Cu3O7−δ. Josephson effect [1] is a phenomenon, where it is possible to observe persistent and phase-dependent current in tunnel structures (weak link):
 (1)
(1)
 (2)
(2)
 (3)
(3)
where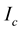 ―critical current,
―critical current, ―“phase difference” across the junction,
―“phase difference” across the junction, ―voltage,
―voltage,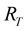 ―tunneling conductance. In our case junction is exposed to radiation, thus we have:
―tunneling conductance. In our case junction is exposed to radiation, thus we have:  which gives us the next equation for Josephson current:
which gives us the next equation for Josephson current:
 .
.
From this equation, it follows that under irradiation of Josephson junction it is possible to observe steps on a current-voltage characteristic with 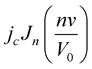 amplitude. The experiment conditions corresponded to so-called inverse non-stationary Josephson effect with external electromagnetic microwave radiation (in our case
amplitude. The experiment conditions corresponded to so-called inverse non-stationary Josephson effect with external electromagnetic microwave radiation (in our case
 ). We observed Shapiro steps on the curve of the current-voltage characteristic that pointed on an appearance of Josephson effect [1] [2] , and enabled drawing a conclusion about high microwave radiation sensitivity of the contact (Figure 1). Also it’s worth mentioning that our junction is cheap and easy to produce; that’s very important in case of breakdown. So it is viable to construct a fast spectrum analyzer with the high microwave radiation sensitivity based on HTSP Josephson junction [3] . Such a device could record THz radiation, as
). We observed Shapiro steps on the curve of the current-voltage characteristic that pointed on an appearance of Josephson effect [1] [2] , and enabled drawing a conclusion about high microwave radiation sensitivity of the contact (Figure 1). Also it’s worth mentioning that our junction is cheap and easy to produce; that’s very important in case of breakdown. So it is viable to construct a fast spectrum analyzer with the high microwave radiation sensitivity based on HTSP Josephson junction [3] . Such a device could record THz radiation, as , and Y1Ba2Cu3O7−δ possesses a wider superconductivity gap Δ in comparison with traditional superconductors. The action of the analyzer comes to recording current-voltage characteristic, recognition of Shapiro steps, and restoration of signal spectrum based on them.
, and Y1Ba2Cu3O7−δ possesses a wider superconductivity gap Δ in comparison with traditional superconductors. The action of the analyzer comes to recording current-voltage characteristic, recognition of Shapiro steps, and restoration of signal spectrum based on them.
2. Method of Analogy Simulating of the Quantum Computer with the Help of the Single Josephson Contact: Discussion of the Scheme of the Device
One of the most interesting modern problems, which demand quick production of Fourier transform, is the realization of quantum computer [4] . At present, there are a lot of research centers, which try to find ways of realization of quantum computer. Yet, there is the only applied problem for such a devise. It is the problem of factorization of multidigit numbers,which provides the framework for code-breakingof the high defensive codes in cryptography [5] . The method of factorization is based on the classical Euclid algorithm [6] . For factorization of an integer number  on prime factors it is necessary to find periods of the function
on prime factors it is necessary to find periods of the function , where
, where  is the residue of division
is the residue of division  by
by ,
, ―natural number. Then one takes the lowest period
―natural number. Then one takes the lowest period , and defines the proper divisor
, and defines the proper divisor , where
, where  is the greatest common divisor of
is the greatest common divisor of  and
and .
.
This simple algorithm for solving the problem of factorization of numbers could be realized with the help of quantum computer. As the period of function  corresponds to the maximum of its Fourier-spectrum, it is enough to find appropriate coordinates of the extremum. The quantum computer permits to do such operation for a few measurements of
corresponds to the maximum of its Fourier-spectrum, it is enough to find appropriate coordinates of the extremum. The quantum computer permits to do such operation for a few measurements of  register. Registers
register. Registers  and
and  form entangled state, when all combinations of
form entangled state, when all combinations of 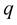 -bites, which correspond to domain of
-bites, which correspond to domain of  definition, are present at the
definition, are present at the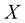 , due to quantum fluctuation and appropriate values of
, due to quantum fluctuation and appropriate values of  are in register
are in register . We propose alternative approach for finding an effective substitution of the non-polynominal algorithm, which is based on the use of a spectrum analyzer with Josephson HTSP junction. In our case the role of quantum parallelism is substituted by the modeling of function
. We propose alternative approach for finding an effective substitution of the non-polynominal algorithm, which is based on the use of a spectrum analyzer with Josephson HTSP junction. In our case the role of quantum parallelism is substituted by the modeling of function . Indeed, as a periodic function
. Indeed, as a periodic function  contains the whole superposition (not quantum) of Fourier harmonics, which form this function supposing time
contains the whole superposition (not quantum) of Fourier harmonics, which form this function supposing time  is fixed, when it is multiple of the period
is fixed, when it is multiple of the period . In some way this is an analog of the quantum parallelism, when register
. In some way this is an analog of the quantum parallelism, when register  of a quantum computer contains in the form of superposition all possible values of
of a quantum computer contains in the form of superposition all possible values of  due to indefinite states of all
due to indefinite states of all  -bits. The block scheme of such device, which includes Josephson junction and is intended for factorization of numbers on prime factors, is presented on Figure 2. Here, voltage
-bits. The block scheme of such device, which includes Josephson junction and is intended for factorization of numbers on prime factors, is presented on Figure 2. Here, voltage  is applied to M1, thus the output of integrator is
is applied to M1, thus the output of integrator is . Further, in accordance with Richardson formula we observe current
. Further, in accordance with Richardson formula we observe current
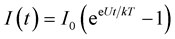 on diode
on diode , and by zero shifting of integrator M2 we can compensate term
, and by zero shifting of integrator M2 we can compensate term  in order to receive
in order to receive  on M3 input (we assume for convenient that
on M3 input (we assume for convenient that , thus
, thus ). Next we compare
). Next we compare  with the analog signal
with the analog signal  (it is generated via M7) on comparator M4. If
(it is generated via M7) on comparator M4. If  exceeds
exceeds , then M4 generates pulse with amplitude, which is defined by M7 and M5. These pulses form step stair function after integrating on M6. Difference between signal
, then M4 generates pulse with amplitude, which is defined by M7 and M5. These pulses form step stair function after integrating on M6. Difference between signal  and step stair function is residue-
and step stair function is residue-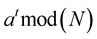 ,
,

Figure 1. Rightand left-hand bolts are identical constructively. They have different thread pitch between higher and lower parts, that allows to displace electrodes of HTSP toward/outward by 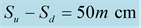 per one turn. Junction is shifted out of center for additional accuracy of adjustment of contact, that permit to use principle of lever.
per one turn. Junction is shifted out of center for additional accuracy of adjustment of contact, that permit to use principle of lever.
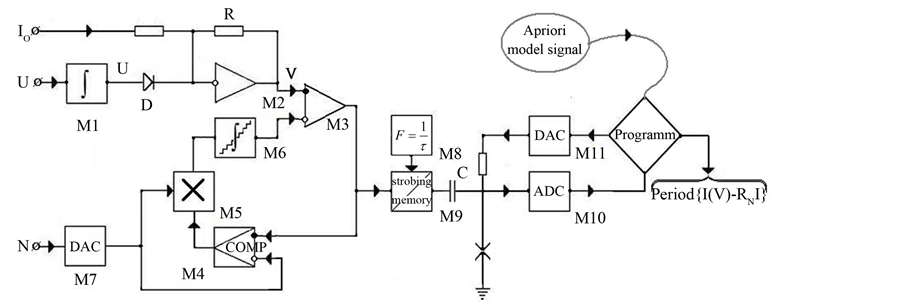
Figure 2. The block scheme demonstrates the realization of process of factorization on prime factors via Fourier spectrum analyzer, which is based on HTSP Josephson junction. Left-hand out of the capacity C (M1 - M8)—block of formation of . Right-hand out of C (M9 - M11)—Josephson spectrum analyzer. M1—integrator with a constant voltage at the entrance; M2—integrator of currents; M3—wide band differential operational amplifier; M4—comparator; M5—digital analog multiplier; M6—stepped integrator; M7—digital-to-analog converter; M8—tact generator; M9—strobe storage memory; cross-Josephson junction; M10—digital-to-analog converter; M11—analog-to-digital converter.
. Right-hand out of C (M9 - M11)—Josephson spectrum analyzer. M1—integrator with a constant voltage at the entrance; M2—integrator of currents; M3—wide band differential operational amplifier; M4—comparator; M5—digital analog multiplier; M6—stepped integrator; M7—digital-to-analog converter; M8—tact generator; M9—strobe storage memory; cross-Josephson junction; M10—digital-to-analog converter; M11—analog-to-digital converter.
which is needed for prime numbers factorization. From M3 residue is applied to M8, and after discretization it is applied to Josephson junction, where Fourier conversion is occurred.
3. Conclusion
Of course, during development, analog computing systems yielded to digital one in produced calculations. However, in our opinion in the field of quantum computers that moment will not come very soon.
Acknowledgements
This work was supported by the program “Strongly Correlated Electrons in Semiconductors, Metals, Superconductors and Magnetic Materials” of the Department of Physical Sciences of the Russian Academy of Sciences (project No. II-3).