Distribution of the Sample Correlation Matrix and Applications ()
1. Introduction
The correlation matrix plays an important role in multivariate analysis since by itself it captures the pairwise degrees of relationship between different components of a random vector. Its presence is very visible in Principal Component Analysis and Factor Analysis, where in general, it gives results different from those obtained with the covariance matrix. Also, as a test criterion, it is used to test the independence of variables, or subsets of variables ([1] , p. 407).
In a normal distribution context, when the population correlation matrix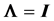 , the identity matrix, or equivalently, the population covariance matrix
, the identity matrix, or equivalently, the population covariance matrix 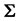 is diagonal, i.e.
is diagonal, i.e.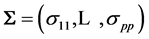 , the distribution of the sample correlation matrix R is relatively easy to compute, and its determinant has a distribution that can be expressed as a Meijer G-function distribution. But when
, the distribution of the sample correlation matrix R is relatively easy to compute, and its determinant has a distribution that can be expressed as a Meijer G-function distribution. But when 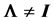 no expression for the density of R is presently available in the literature, and the distribution of its determinant is still unknown, in spite of efforts made by several researchers. We will provide here the closed form expression of the distribution of R, with the sample variances as parameters, hence complementing a result presented by Fisher in [2] .
no expression for the density of R is presently available in the literature, and the distribution of its determinant is still unknown, in spite of efforts made by several researchers. We will provide here the closed form expression of the distribution of R, with the sample variances as parameters, hence complementing a result presented by Fisher in [2] .
As explained in [3] , for a random matrix, there are at least three distributions of interest, its “entries distribution” which gives the joint distribution of its matrix entries, its “determinant distribution” and its “latent roots distribution”. We will consider the first two only and note that, quite often, the first distribution is also expressed in terms of the determinant, and can lead to some confusion. In Section 2 we recall some results related to the case where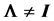 , and establish the new exact expression of the density of R, with the sample variances
, and establish the new exact expression of the density of R, with the sample variances 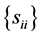 as parameters, denoted
as parameters, denoted . In Section 3, some simulation results are given. The distribution of
. In Section 3, some simulation results are given. The distribution of , the determinant of R, is given in Section 4 for
, the determinant of R, is given in Section 4 for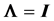 . Applications of the above results to the concept of dependence within a multi-component system are given in Section 5. Numerical examples are given throughout the latter part of the paper to illustrate the results.
. Applications of the above results to the concept of dependence within a multi-component system are given in Section 5. Numerical examples are given throughout the latter part of the paper to illustrate the results.
2. Case of the Population Correlation Matrix Not Being Identity
2.1. Covariance and Correlation Matrices
Let us consider a random vector X with mean 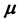 and covariance matrix
and covariance matrix , of the form of a (p × p) symmetric positive definite random matrix
, of the form of a (p × p) symmetric positive definite random matrix
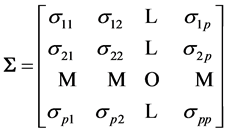
of pairwise covariances between components in the matrix.
We obtain the population correlation matrix  by diving each
by diving each 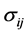 by
by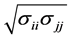 . Then
. Then
 , where
, where , is symmetrical, with diagonals
, is symmetrical, with diagonals ,
, 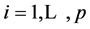 , i.e.
, i.e.
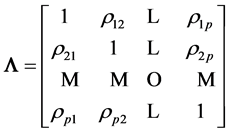 .
.
For a sample of size n of observations from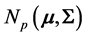 , the sample mean
, the sample mean 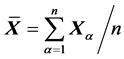 and the “adjusted sample covariance” matrix
and the “adjusted sample covariance” matrix
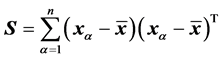 , (1)
, (1)
(or matrix of sums of squares and products, ) are independent, with the latter having a Wishart distribution
) are independent, with the latter having a Wishart distribution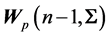 . Similarly, the correlation matrix
. Similarly, the correlation matrix 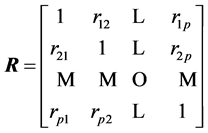 is obtained from S by using the relations:
is obtained from S by using the relations: , or
, or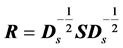 , where
, where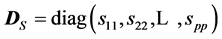 . We also have the relation between determinants:
. We also have the relation between determinants: , and, similarly,
, and, similarly, .
.
It is noted that by considering the usual sample covariance matrix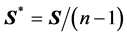 , which is
, which is
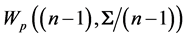 , we have the relation
, we have the relation , between the two diagonal elements, but the sample correlation matrix is the same.
, between the two diagonal elements, but the sample correlation matrix is the same.
The  coefficients
coefficients 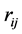 are (marginally) distributed independently of both the sample and population means [2] . It is to be noticed that while R can always be defined from S, the reverse is not true since S has
are (marginally) distributed independently of both the sample and population means [2] . It is to be noticed that while R can always be defined from S, the reverse is not true since S has  independent parameters. This fact explains the differences between results when either R or S is used.
independent parameters. This fact explains the differences between results when either R or S is used.
In the bivariate case, Hotelling’s expression [4] clearly shows that the density of r depends only on the population correlation coefficient 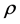 and the sample size n (see Section 4.3) and we will see that, similarly, the density of the sample correlation matrix, with the sample variances as parameters, is dependent on the population variances and the sample size. However,
and the sample size n (see Section 4.3) and we will see that, similarly, the density of the sample correlation matrix, with the sample variances as parameters, is dependent on the population variances and the sample size. However, 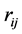 are biased estimators of
are biased estimators of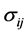 , and Olkin and Pratt [5] have suggested using the modified estimator
, and Olkin and Pratt [5] have suggested using the modified estimator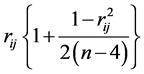 , with a table of corrective multipliers for
, with a table of corrective multipliers for 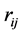 for convenience.
for convenience.
2.2. Some Related Work
Several efforts have been carried out in the past to obtain the exact form of the density of R for the general case, where ,
,  and
and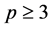 . For example, Joarder and Ali [6] derived the distribution of R for a class of elliptical models. Ali, Fraser and Lee [7] , starting from the identity correlation matrix case, derived the density for the general case when
. For example, Joarder and Ali [6] derived the distribution of R for a class of elliptical models. Ali, Fraser and Lee [7] , starting from the identity correlation matrix case, derived the density for the general case when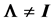 , again by modulating the likelihood ratio to obtain a density of R containing the function
, again by modulating the likelihood ratio to obtain a density of R containing the function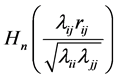 , already used by Fraser ([8] , p. 196) in the bivariate case. But here,
, already used by Fraser ([8] , p. 196) in the bivariate case. But here, 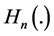 , expressed as an infinite series, has a much more complicated expression. Schott ([9] , p. 408), using
, expressed as an infinite series, has a much more complicated expression. Schott ([9] , p. 408), using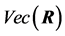 , gives for a first-order approximation for R and the expression of
, gives for a first-order approximation for R and the expression of , and Kollo and Ruul [10] , also using
, and Kollo and Ruul [10] , also using , presented a general method for approximating the density of R through another multivariate density, possibly one of higher dimension. Finally, Farrell ([11] , p. 177) has approached the problem using exterior differential forms. However, no explicit expression for the density of R is given in any of these works, and the question rightly raised is whether that such an expression really exists.
, presented a general method for approximating the density of R through another multivariate density, possibly one of higher dimension. Finally, Farrell ([11] , p. 177) has approached the problem using exterior differential forms. However, no explicit expression for the density of R is given in any of these works, and the question rightly raised is whether that such an expression really exists.
2.3. Some New Results
We begin with the case of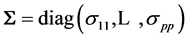 . Then it can be easily established that the density of R is ([12] , p. 107):
. Then it can be easily established that the density of R is ([12] , p. 107):
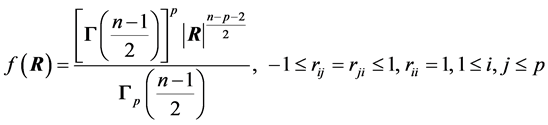 (2)
(2)
By showing that the joint density of the diagonal elements 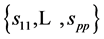 with R, denoted
with R, denoted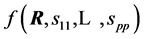 , can be factorized into the product of two densities,
, can be factorized into the product of two densities,  and
and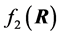 , which has expression (2) above.
, which has expression (2) above.  and R are hence independent.
and R are hence independent.
We can also show that (2) is a density, i.e. it integrates to 1 within its definition domain, by using the approach given in Mathai and Haubold ([13] , p. 421), based on matrix decomposition.
In what follows, following Kshirsagar’s approach [14] , which itself is a variation of Fisher’s [2] original method, we establish first the expression of a similar joint distribution, when 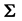 is not diagonal.
is not diagonal.
THEOREM 1:
Let  , where we suppose that the population correlation
, where we suppose that the population correlation 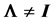 and its inverse
and its inverse 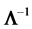 has
has 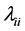 as its diagonal elements. Then the correlation matrix R of a random sample of n observations has its distribution given by:
as its diagonal elements. Then the correlation matrix R of a random sample of n observations has its distribution given by:
 , (3)
, (3)
where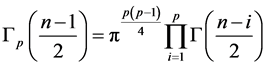 , with the sample covariance
, with the sample covariance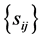 ,
,  , serving as parameters.
, serving as parameters.
PROOF: Let us consider the “adjusted sample covariance matrix” S, given by (1). We know that 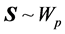
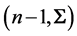 , with density:
, with density:
 with C being an appropriate constant.
with C being an appropriate constant.
Our objective is to find the joint density of R with a set of variables 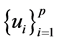 so that the density of R can be obtained by integrating out the variables
so that the density of R can be obtained by integrating out the variables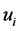 .
.
Let 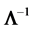 be the inverse of
be the inverse of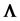 , the (population) matrix of correlations, with diagonals
, the (population) matrix of correlations, with diagonals ,
,  and non-diagonals
and non-diagonals ,
, 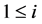 ,
, . We first transform the
. We first transform the 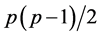 variables
variables ,
, 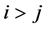 , into
, into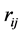 . Since the diagonal
. Since the diagonal  remain unchanged, the Jacobian of the transformation from S to
remain unchanged, the Jacobian of the transformation from S to 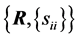 is then
is then 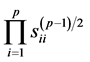 and the new joint density is:
and the new joint density is:
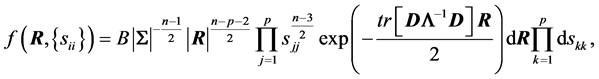
where 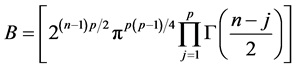 and
and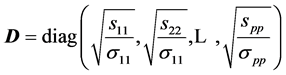 .
.
We set
 (4)
(4)
with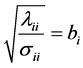 , and form the symmetric matrix
, and form the symmetric matrix
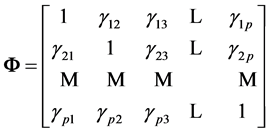 , (5)
, (5)
where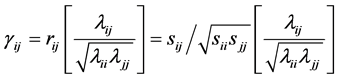 , which depends on S.
, which depends on S.
The joint density of 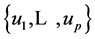 and R is now:
and R is now:
 .
.
R and  are independent only if the above expression can be expressed as the product
are independent only if the above expression can be expressed as the product
 , which is not the case since
, which is not the case since  contains
contains .
.
To integrate out the vector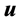 , we set
, we set
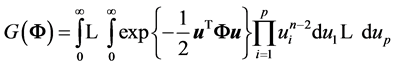 ,
,
(This integral is denoted  by Fisher [2] , and by
by Fisher [2] , and by  by Kshirsagar [14] who used the notation
by Kshirsagar [14] who used the notation  and, in both instances, was left non-computed).
and, in both instances, was left non-computed).
Hence, if  is constant, as in the case when
is constant, as in the case when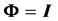 , R would have density
, R would have density
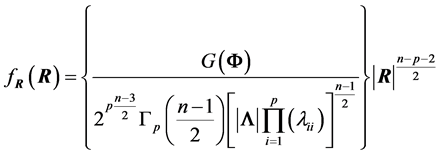 , (6)
, (6)
with , being the p-gamma function. However, in the general case this is not true.
, being the p-gamma function. However, in the general case this is not true.
Consider the quadratic form:
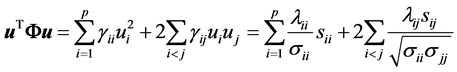 and
and
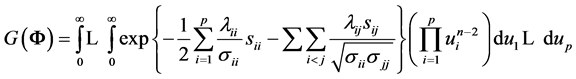 .
.
Changing to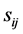 , we have
, we have
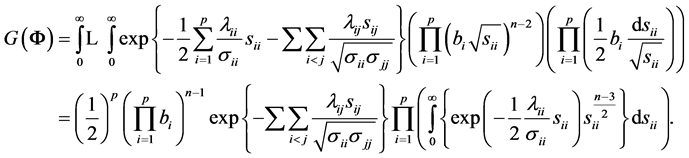
Since each integral is a gamma density in , with value
, with value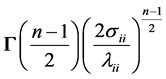 , we obtain
, we obtain
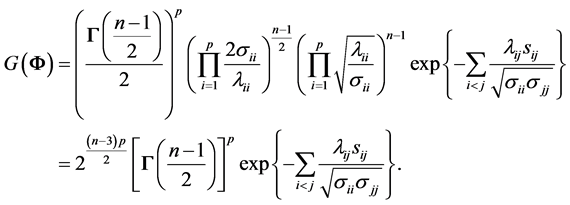
 contains all non-diagonal entries of the sample covariance matrix, and depends on S. We now obtain from (6) expression (3) of Theorem 1. Here, the off-diagonal sample covariance,
contains all non-diagonal entries of the sample covariance matrix, and depends on S. We now obtain from (6) expression (3) of Theorem 1. Here, the off-diagonal sample covariance, 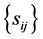 , serve as parameters of this density.
, serve as parameters of this density.
QED.
Alternately, using the corresponding correlation coefficients, we have:
 , (7)
, (7)
REMARKS:
1) For  our results given above should reduce to known results, and they do. Indeed, since we now have
our results given above should reduce to known results, and they do. Indeed, since we now have 
 .
.
Hence,
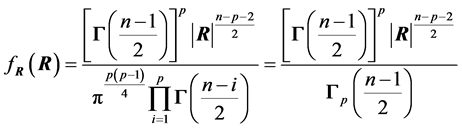
as in (2) since we now have .
.
Here, only the value of p needs to be known and this explains why expression (2) depends only on n and p. Also, as pointed out by Muirhead ([15] , p. 148), if we do not suppose normality, the same results can be obtained under some hypothesis.
2) Expression (3) can be interpreted as the density of R when 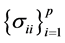 are known, and
are known, and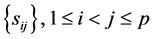 , is a set of constant sample covariances. But when this set is considered as a random vector, with a certain distribution,
, is a set of constant sample covariances. But when this set is considered as a random vector, with a certain distribution, 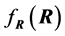 is called mixture distribution, defined in two steps:
is called mixture distribution, defined in two steps:
a) 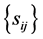 has an (known or unknown) distribution
has an (known or unknown) distribution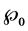 , i.e.
, i.e. .
.
b) (R;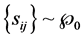 ) has the density given by (3), denoted
) has the density given by (3), denoted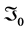 .
.
The distribution of R is then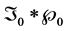 , where * denotes the mixture operation.
, where * denotes the mixture operation.
However, a closed form for this mixture is often difficult to obtain.
Alternately,  could be
could be , with
, with 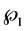 being the density of the diagonal sample variances
being the density of the diagonal sample variances 
and off-diagonal sample correlations,  while
while 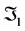 is given by (7).
is given by (7).
3) We have, using (3), and the relation  the following equivalent expression, where
the following equivalent expression, where 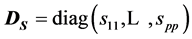 :
:
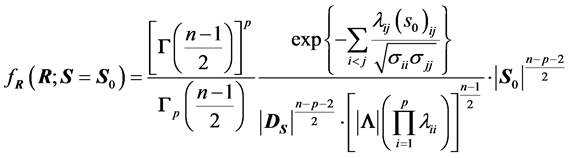 . (8)
. (8)
Expression (8) gives the positive numerical value of 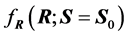 upon knowledge of the value of S. It will serve to set up simulation computations in Section 3. However, it also shows that
upon knowledge of the value of S. It will serve to set up simulation computations in Section 3. However, it also shows that 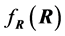 can be defined with S, and when S has a certain distribution the values of
can be defined with S, and when S has a certain distribution the values of  are completely determined with that distribution. This highlights again the fact that, in statistics, using R or S can lead to different results, as mentioned previously.
are completely determined with that distribution. This highlights again the fact that, in statistics, using R or S can lead to different results, as mentioned previously.
2.4. Other Known Results
1) The distribution of the sample coefficient of correlation in the bivariate normal case can be determined fairly directly when integrating out 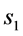 and
and , and this fact is mentioned explicitly by Fisher ([2] , p. 4), who stated: “This, however, is not a feasible path for more than two variables.” In the bivariate case,
, and this fact is mentioned explicitly by Fisher ([2] , p. 4), who stated: “This, however, is not a feasible path for more than two variables.” In the bivariate case,
 , and has been well-studied by several researchers, using different approaches and, as early as 1915, Fisher [16] gave its density as:
, and has been well-studied by several researchers, using different approaches and, as early as 1915, Fisher [16] gave its density as:
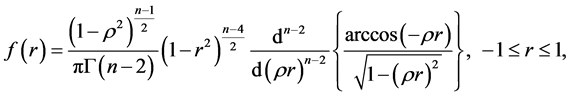 (9)
(9)
Using geometric arguments, with 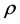 being the population coefficient of correlation. We refer to ([17] , p. 524-534) for more details on the derivation of the above expression. Other equivalent expressions, reportedly as numerous as 52, were obtained by other researchers, such as Hotelling [4] , Sawkins [18] , Ali et al. [7] .
being the population coefficient of correlation. We refer to ([17] , p. 524-534) for more details on the derivation of the above expression. Other equivalent expressions, reportedly as numerous as 52, were obtained by other researchers, such as Hotelling [4] , Sawkins [18] , Ali et al. [7] .
2) Using Equation (3) on the sample correlation matrix , obtained from the sample covariance matrix
, obtained from the sample covariance matrix
 Together with p = 2, we can also arrive at one of these forms (see also Section 4.3, where the determinant of R provides a more direct approach).
Together with p = 2, we can also arrive at one of these forms (see also Section 4.3, where the determinant of R provides a more direct approach).
3) Although Fisher [2] did not give the explicit form of the integral 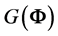 above, he included several interesting results on
above, he included several interesting results on , as a function of the sample size n and coefficients
, as a function of the sample size n and coefficients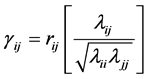 . For example, in the case all
. For example, in the case all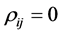 ,
, 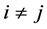 , the generalized volume in the p(p − 1)/2-dimension space of the region of integration for rij is found to be a function of p, having a maximum at p = 6. In the case all
, the generalized volume in the p(p − 1)/2-dimension space of the region of integration for rij is found to be a function of p, having a maximum at p = 6. In the case all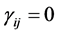 , the expressions of the partial derivatives of Log
, the expressions of the partial derivatives of Log w.r.t.
w.r.t.  can be obtained, and so are the mixed derivatives.
can be obtained, and so are the mixed derivatives.
For the case n = 2, and p = 3,  has an interesting geometrical interpretation as
has an interesting geometrical interpretation as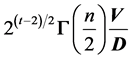 , where V = generalized volume defined by
, where V = generalized volume defined by 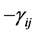 and D is the volume defined by the p unit vectors in a transformation where
and D is the volume defined by the p unit vectors in a transformation where 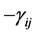 are the cosines of the angles between pairs of edges.
are the cosines of the angles between pairs of edges.
3. Some Computation and Simulation Results
3.1. Simulations Related to R
A matrix equation such as (3) can be difficult to visualize numerically, especially when the dimensions are high, i.e. . Ideally, to illustrate (7), a figure giving
. Ideally, to illustrate (7), a figure giving 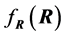 in function of the matrix R itself is most informative, but, naturally, impossible to obtain. One question we can investigate is how the values of
in function of the matrix R itself is most informative, but, naturally, impossible to obtain. One question we can investigate is how the values of  distributed, for a normal model
distributed, for a normal model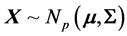 ? Simulation using (8) can provide some information on this distribution in some specific cases. For example, we can start from the (4 × 4) population covariance matrix
? Simulation using (8) can provide some information on this distribution in some specific cases. For example, we can start from the (4 × 4) population covariance matrix
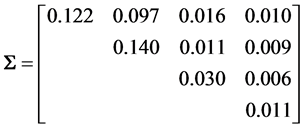 taken from our analysis of Fisher’s iris data [19] . It concerns the Setosa iris variety, with x1 = sepal length, x2 = sepal with, x3 = petal length and x4 = petal width. It gives the population correlation matrix
taken from our analysis of Fisher’s iris data [19] . It concerns the Setosa iris variety, with x1 = sepal length, x2 = sepal with, x3 = petal length and x4 = petal width. It gives the population correlation matrix
 where all
where all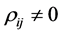 . We generate 10,000 samples of 100 observations each from
. We generate 10,000 samples of 100 observations each from , which give 10,000 values of the covariance matrix S, which, in turn, give matrix values for R, scalar values for
, which give 10,000 values of the covariance matrix S, which, in turn, give matrix values for R, scalar values for 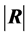 and, finally, positive scalar values for
and, finally, positive scalar values for , as given by (8). Recall that for X normal S has a Wishart distribution
, as given by (8). Recall that for X normal S has a Wishart distribution . Figure 1 gives the corresponding histogram, which shows that values of W are distributed along a unimodal density, denoted by
. Figure 1 gives the corresponding histogram, which shows that values of W are distributed along a unimodal density, denoted by , with a very small variation interval, i.e. most of its values are concentrated around the mode.
, with a very small variation interval, i.e. most of its values are concentrated around the mode.
Note: A special approach to graphing distributions of covariance matrices, using the principle of decomposing a matrix into scale parameters and correlations, is presented in: Tokuda, T., Goodrich, B., Van Mechelen, I., Gelman, A. and Tuerlinckx, F., Visualizing Distributions of Covariance Matrices (Document on the Internet).
It is also mentioned there that for the Inverted Wishart case, with  degrees of freedom, then
degrees of freedom, then
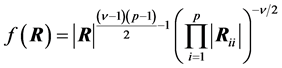 where
where  is the i-th principal sub-matrix of R, obtained by removing row and column i (p. 12).
is the i-th principal sub-matrix of R, obtained by removing row and column i (p. 12).
3.2. Simulations Related to 
Similarly, the same application above gives the approximate simulated distribution of  presented in Figure 2. We can see that it is a unimodal density which depends on the correlation coefficients
presented in Figure 2. We can see that it is a unimodal density which depends on the correlation coefficients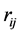 .
.
Using expression (7), which exhibits explicitely rij, and replacing rij by the corrected value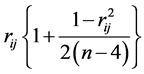 the unbiased estimator of
the unbiased estimator of , we obtain
, we obtain . However, since an unbiased estimator of
. However, since an unbiased estimator of 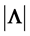 is still to be found we cannot use neither
is still to be found we cannot use neither 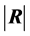 nor
nor 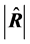 as point-estimate of
as point-estimate of . Figure 2 gives the simulated distributions of
. Figure 2 gives the simulated distributions of 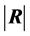 and of
and of . We can see that the two approximate densities are different, and the density of
. We can see that the two approximate densities are different, and the density of  has higher mean and median, resulting in a shift to the right. But, again, the two variation intervals are very small.
has higher mean and median, resulting in a shift to the right. But, again, the two variation intervals are very small.
3.3. Expression of 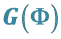
In the proof of Theorem 1, we have established that
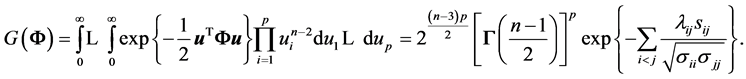
Using the above matrix , for a simulated sample, say
, for a simulated sample, say
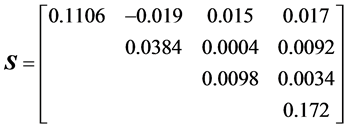 we compute directly the left side by numerical integration, and the right side by using the algebraic expression. The results are extremely close to each other, with both around the numerical value 1.238523012 × 105.
we compute directly the left side by numerical integration, and the right side by using the algebraic expression. The results are extremely close to each other, with both around the numerical value 1.238523012 × 105.
4. Distribution of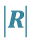 , the Determinant of R
, the Determinant of R
First, let det(R) be denoted by . In this case
. In this case , this distribution is very complex and no related result is known when
, this distribution is very complex and no related result is known when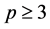 . Nagar and Castaneda [20] , for example, established some results in the general case, for p = 2.
. Nagar and Castaneda [20] , for example, established some results in the general case, for p = 2.
Theoretically, we can obtain the density of  from (3) by applying the transformation
from (3) by applying the transformation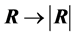 , with differential
, with differential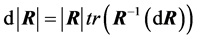 , but the expression obtained quickly becomes intractable. Only in the case of
, but the expression obtained quickly becomes intractable. Only in the case of 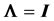 that we can derive some analytical results on
that we can derive some analytical results on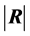 , as presented in the next section. Gupta and Nagar [21] established some results for the case of a mixture of normal models, but again under the hypothesis of
, as presented in the next section. Gupta and Nagar [21] established some results for the case of a mixture of normal models, but again under the hypothesis of .
.
4.1. Density of the Determinant 
When considering Meijer G-functions and their extensions, Fox’s H-functions [22] , for  the density of
the density of  can be expressed in closed forms, as are those of other related multivariate statistics [23] . Let us recall that the Meijer function
can be expressed in closed forms, as are those of other related multivariate statistics [23] . Let us recall that the Meijer function , and the Fox function
, and the Fox function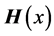 , are defined as follows:
, are defined as follows:  is the integral along the complex contour L of a rational expression of Gamma functions
is the integral along the complex contour L of a rational expression of Gamma functions
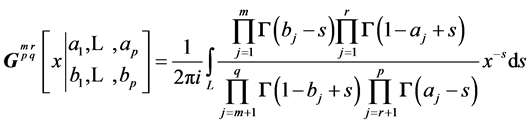 (10)
(10)
It is a special case, when 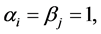
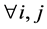 , of Fox’s H-function, defined as:
, of Fox’s H-function, defined as:
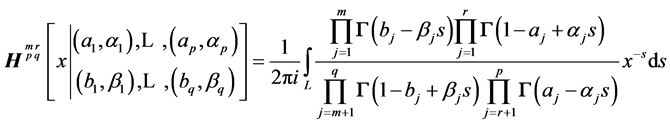 .
.
Under some fairly general conditions on the poles of the gamma functions in the numerator, the above integrals exist.
THEOREM 2: When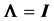 , for a random sample of size n from
, for a random sample of size n from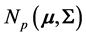 , the density of
, the density of 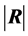 depends only on n and p:
depends only on n and p:
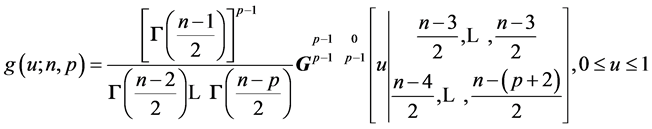 . (11)
. (11)
PROOF:
From (2) the moments of order t of  are:
are:
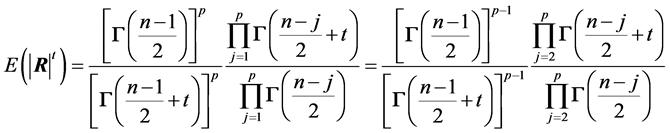 , (12)
, (12)
 , which is a product of moments of order t of independent beta variables. Upon identification of (12) with these products, we can see that
, which is a product of moments of order t of independent beta variables. Upon identification of (12) with these products, we can see that , with
, with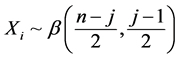 , with
, with . Using [23] the product of k independent betas,
. Using [23] the product of k independent betas, 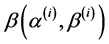 , has as density
, has as density
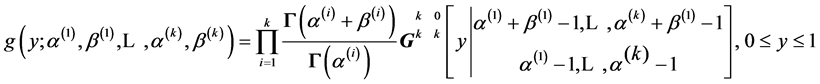
Hence, we have here, the density of  as:
as:
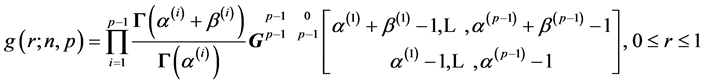 where
where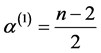 ,
, 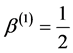 ,
,  ,
, 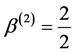 and
and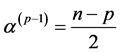 ,
, .
.
And, hence, we obtain:
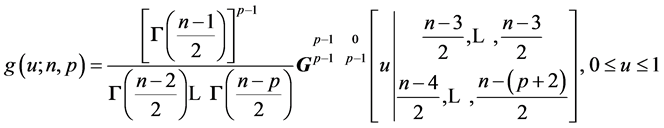 (13)
(13)
QED.
The density of  can easily be computed and graphed, and percentiles of
can easily be computed and graphed, and percentiles of  can be determined numerically. For example, for p = 4, n = 8. The 2.5th and 97.5th percentiles can be found to be 0.04697 and 0.7719 respectively.
can be determined numerically. For example, for p = 4, n = 8. The 2.5th and 97.5th percentiles can be found to be 0.04697 and 0.7719 respectively.
4.2. Product and Ratio
Let  and
and  be two independent correlation matrices, obtained from 2 populations, each with zero population correlation coefficients. The determinant of their product is also a G-function distribution, and its density can be obtained. This result is among those which extend relations obtained in the univariate case by Pham-Gia and Turkkan [24] , and also has potential applications in several domains.
be two independent correlation matrices, obtained from 2 populations, each with zero population correlation coefficients. The determinant of their product is also a G-function distribution, and its density can be obtained. This result is among those which extend relations obtained in the univariate case by Pham-Gia and Turkkan [24] , and also has potential applications in several domains.
THEOREM 3: Let  and
and 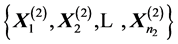 be two independent random samples from
be two independent random samples from  and
and  respectively, both
respectively, both  being diagonal. Then the determinant
being diagonal. Then the determinant  of the product
of the product 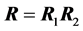 of the two correlation matrices
of the two correlation matrices  and
and 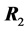 has density:
has density:
 , (14)
, (14)
where  and
and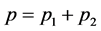 .
.
PROOF: Immediate by using multiplication of G-densities presented in [23] .
QED.
Figure 3 shows the density of , for
, for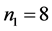 ,
, 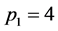 and
and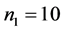 ,
, .
.
Using again results presented in [23] we can similarly derive the density of the ratio 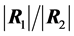 in terms of G-functions. Its expression is not given here to save space but is available upon request.
in terms of G-functions. Its expression is not given here to save space but is available upon request.
4.3. Particular Cases
1) Bivariate normal case: a) for the bivariate case we have , and when
, and when 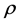 is zero, we have from (11) the density of
is zero, we have from (11) the density of 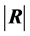 as
as
 which is the G-function form of the beta
which is the G-function form of the beta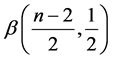 . Hence, the distribution of
. Hence, the distribution of 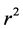 is:
is: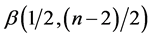 ,
, 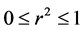 , and the density of r is:
, and the density of r is:
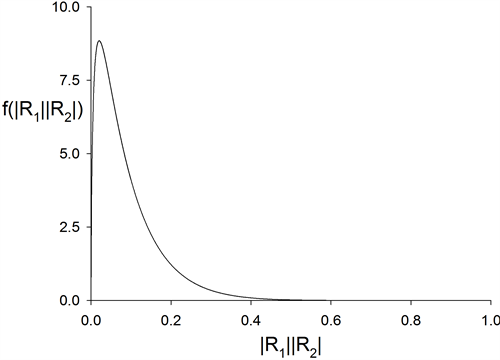
Figure 3. Density of product of independent correlation determinants.
 , (15)
, (15)
for . Testing
. Testing 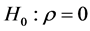 is much simpler when using Student’s t-distribution,
is much simpler when using Student’s t-distribution,  , and is covered in most textbooks.
, and is covered in most textbooks.
Pitman [25] has given an interesting distribution-free test when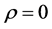 .
.
2) When  Hotelling ([4] ) gave the density of
Hotelling ([4] ) gave the density of 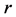 as:
as:
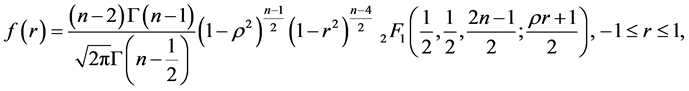 (16)
(16)
where 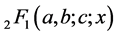 is Gauss hypergeometric function with parameters
is Gauss hypergeometric function with parameters 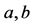 and c.
and c.
3) Mixture of Normal Distributions: With X coming now from the mixture: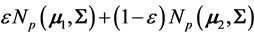 ,
,
 , Gupta and Nagar [21] consider
, Gupta and Nagar [21] consider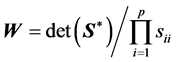 , and give the density of W in terms of Meijer G-functions, but for the case
, and give the density of W in terms of Meijer G-functions, but for the case 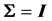 only. The complicated form of this density contains the hypergeometric function
only. The complicated form of this density contains the hypergeometric function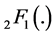 , as expected.
, as expected.
For the bivariate case, Nagar and Castaneda [20] established the density of r and gave its expression for both cases, 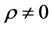 and
and . In the first case the density of r, when only one population is considered, reduces to the expression obtained by Hotelling [4] above.
. In the first case the density of r, when only one population is considered, reduces to the expression obtained by Hotelling [4] above.
5. Dependence between Components of a Random Vector
5.1. Dependence and 
Correlation is useful in multiple regression analysis, where it is strongly related to collinearity. As an example of how individual correlation coefficients are used in regression, the variance inflation factor (VIF), well adopted now in several statistical softwares, measures how much the variance of a coefficient is increased by collinearity, or in other words, how much of the variation in one independent variable is explained by the others. For the j-th variable, 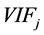 is the j-th diagonal element of
is the j-th diagonal element of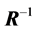 . We know that it equals
. We know that it equals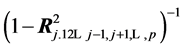 , with
, with 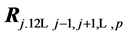 being the multiple correlation of the j-th variable regressed on the remaining
being the multiple correlation of the j-th variable regressed on the remaining 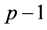 others.
others.
When all correlation measures are considered together, measuring intercorrelation by a single number has been approached in different ways by various authors. Either the value of 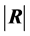 or those of its latent roots can be used. Rencher ([26] , p. 21) mentions six of these measures, among them
or those of its latent roots can be used. Rencher ([26] , p. 21) mentions six of these measures, among them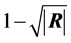 , where
, where 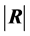 is an observed value of R, and takes the value 1 if the variables are independent, and 0 if there is an exact linear dependence. But since the exact distribution of R is not available this sample measure is rather of descriptive type and no formal inferential process has really been developed.
is an observed value of R, and takes the value 1 if the variables are independent, and 0 if there is an exact linear dependence. But since the exact distribution of R is not available this sample measure is rather of descriptive type and no formal inferential process has really been developed.
Although the notion of independence between different components of a system is of widespread use in the study of the system structure, reliability and performance, its complement, the notion of dependence has been a difficult one to deal with. There are several dependence concepts, as explained by Jogdev [27] , but using the covariance matrix between different components in a joint distribution remains probably the most direct approach. Other more theoretical approaches, are related to the relations between marginal and joint distributions, and Joe [28] can be consulted on these approaches. Still, other aspects of dependence are explored in Bertail et al. [29] . But two random variables can have zero correlation while being dependent. Hence, no-correlation and independence are two different concepts, as pointed out in Drouet Mari and Kotz [30] . Furthermore, for two independent events, the product of their probabilities gives the probability of the intersection event, which is not necessarily the case for two non-correlated events. Fortunately, these two concepts are equivalent, when the underlying population is supposed normal, a hypothesis that we will suppose in this section.
5.2. Inner Dependence of a System
When considering only two variables, several measures of dependence have also been suggested in the literature (Lancaster [31] ), and especially in system reliability (Hoyland and Rausand [32] ), but a joint measure of the degree of dependence between several components of a random vector, or within a system , or inner dependence of
, or inner dependence of , denoted by
, denoted by , is still missing. We approach this dependence concept here by way of the correlation matrix, where a single measure attached to it would reflect the overall degree of dependence. This concept has been presented first in Bekker, Roux and Pham-Gia [33] , to which we refer for more details. It is defined as
, is still missing. We approach this dependence concept here by way of the correlation matrix, where a single measure attached to it would reflect the overall degree of dependence. This concept has been presented first in Bekker, Roux and Pham-Gia [33] , to which we refer for more details. It is defined as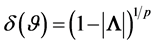 , with
, with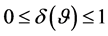 . The measure of independence within the system is then
. The measure of independence within the system is then
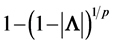 , estimated by
, estimated by , where
, where 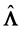 is a point estimation of
is a point estimation of 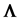 based on R, the correlation matrix associated with a sample of n observations of the p-component system. In the general case this estimation question is still unresolved, except for the binormal case,
based on R, the correlation matrix associated with a sample of n observations of the p-component system. In the general case this estimation question is still unresolved, except for the binormal case, . We then have
. We then have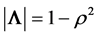 , and
, and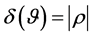 , where
, where 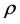 is the coefficient of correlation with its estimation well known, depending on either
is the coefficient of correlation with its estimation well known, depending on either 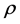 is supposed to be zero or not. The associated sample measure being
is supposed to be zero or not. The associated sample measure being , it is of interest to study the distribution of the sample inner dependence
, it is of interest to study the distribution of the sample inner dependence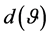 , based on a sample of n observations of the system.
, based on a sample of n observations of the system.
In the language of Reliability Theory, a p-component normal system is fully statistically independent when the  correlation coefficients
correlation coefficients  of its components are all zero. We have:
of its components are all zero. We have:
THEOREM 4: 1) Let the fully statistically independent system 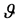 have p components with a joint normal distribution with
have p components with a joint normal distribution with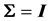 , where
, where .
.
a) Then the distribution of the sample coefficient of inner dependence  is:
is:
 (17)
(17)
b) For the two-component case (p = 2), we have:
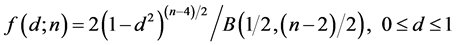 (18)
(18)
2) For a non-fully independent two-component binormal system , for
, for :
:
 (19)
(19)
where 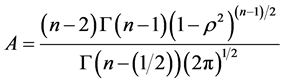 and
and 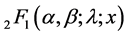 is Gauss hypergeometric function.
is Gauss hypergeometric function.
PROOF: a) For , the density of
, the density of , as given by (17), is obtained from (11) by a change of variable. Figure 4 gives the density of the sample coefficient of inner dependence
, as given by (17), is obtained from (11) by a change of variable. Figure 4 gives the density of the sample coefficient of inner dependence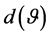 , for n = 10 and p = 4.
, for n = 10 and p = 4.
Expression (18) is obtained from (15) by the change of variable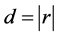 . Again, the density of d, as given by (19), can be derived from (16) by considering the same change of variable. QED.
. Again, the density of d, as given by (19), can be derived from (16) by considering the same change of variable. QED.
Numerical computations give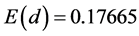 . Estimation of
. Estimation of 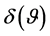 from
from  now follows the same principles as
now follows the same principles as 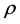 from r.
from r.
Figure 5 gives the density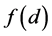 , as given by (19), for n = 8, p = 2,
, as given by (19), for n = 8, p = 2,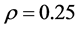 .
.
6. Conclusion
In this article we have established an original expression for the density of the correlation matrix, with the sample variances as parameters, in the case of the multivariate normal population with non-identity population correlation matrix. We have, furthermore, established the expression of the distribution of the determinant of that random matrix in the case of identity population correlation matrix, and computed its value. Applications are
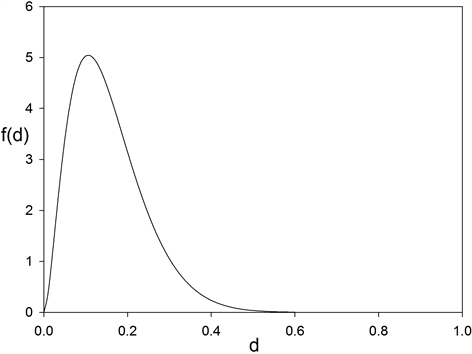
Figure 4. Density (17) for sample coefficient of inner dependence 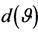 (normal system with four components, n = 10, p = 4).
(normal system with four components, n = 10, p = 4).
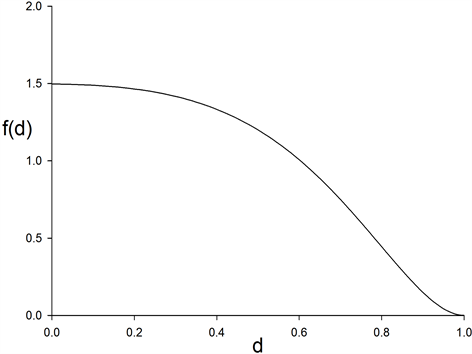
Figure 5. Density (19) of sample measure of a binormal system dependence, .
.
made to the dependence among p components of a system. Also, expressions for the densities of a sample measure of a system inner dependence are established.