1. Introduction
In this paper, we denote by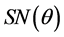 
the skew normal distribution of parameter 
and density :
(1)
where 
and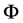 
denote the standard normal 
probability density function and cumulative distribution function, respectively.
The skew normal distribution, due to its mathematical tractability and inclusion of the standard normal distribution, has attracted a lot of attention in the literature. Azzalini [1] , Azzalini [2] , Chiogna [3] , Genton & Liu [4] and Henze [5] discussed basic mathematical and probabilistic properties of the skew normal family. The multivariate skew normal distribution is studied by Azzalini & Capitanio [6] and Azzalini & Dalla Valle [7] . For additional references and a review on related literature, see Azzalini & Capitanio [8] and Pewsey [9] for a collection of papers on the subject. Henze [5] , in his paper showed that if 
and 
are identically and independently distributed 
random variables, then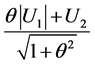 
has the skew normal distribution.
For the simulation of the skew normal distribution, we propose a combinations of maximum and minimum of the independent and identically distributed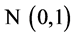 
random variables.
2. Method
Let U1 and U2 two independent and identically distributed 
random variables and 
and
. For simulation of the random variable
, we take the combination of U and V. First note that:
• if
, the density (1) becomes:
, simply simulate
.
• if
, the density (1) becomes:
, we take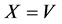
.
• if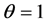
, the density (1) becomes:
, we take
.
For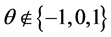
, note :
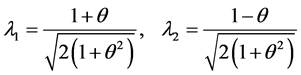(2)
We note that: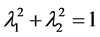
. For simulation of the random variable
, we take the combination of U and V in the form:
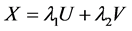(3)
Proposition The random variable X defined in the Equation (3) has the skew normal distribution
.
Proof. The pair 
has density:
, where 
is the indicator function.
Consider the transformation:
. The inverse transform is defined by: 
and the corresponding Jacobian is:
. X density is defined by:
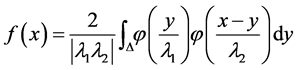(4)
where
. Taking into account
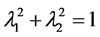, we can write:
(5)
Equation (4) becomes,
(6)
For the domain
, we have the following three cases:
Case 1:
, we have: 
and 
Case 2:
, we have: 
and 
Case 3:
, we have: 
and 
Using Equation (6) and the three cases above, we get the result.
3. Simulation Results
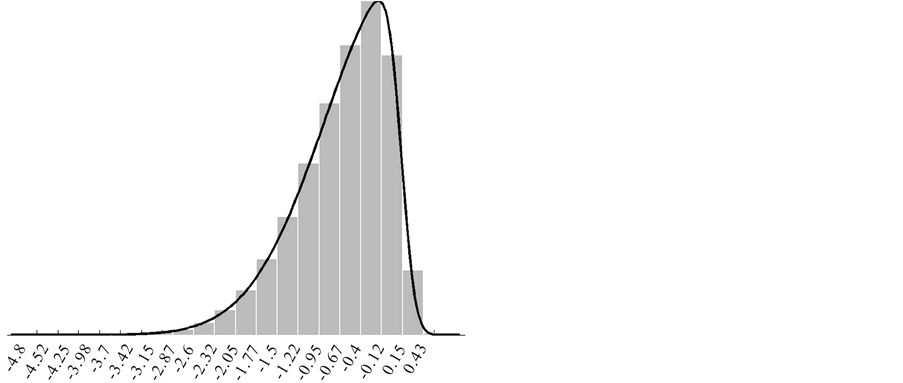
We simulated a sample of size 500,000 for the values 
and
, The following Figure 1, Figure 2 and Table 1, Table 2 show the results obtained by our method and the method Henze [5] .
The results of Table 1 and Table 2 show that our method provides results close to the theoretical values and secondly, we obtain results similar to those obtained by Henze [5] results.
4. Conclusion
In this article we propose a very simple method to simulate skew normal family distribution. The obtained
Table 1 . Simulation results for a sample size of 500,000 and θ = −7.
aby our method; bby the method of Henze [5] .
Table 2. Simulation results for a sample size of 500,000 and θ = 13.
aby our method; bby the method of Henze [5] .
(a)
(b)
Figure 1. Histogram of simulations for a sample size of 500,000 and θ = −7. (a) histogram of simulations using our method; (b) histogram of simulations using the method of Henze [5] .
(a)
(b)
Figure 2. Histogram of simulations for a sample size of 500,000 and θ = 13. (a) histogram of simulations using our method; (b) histogram of simulations using the method of Henze [5] .
results are very close to theoretical values and the method is more efficient than the standard one. The method is simple to program and exploit for practical applications.