1. Introduction
Dual numbers had been introduced by W.K. Clifford (1845-1849) as a tool for his geometrical investigations. After him, E. Study (1860-1930) used dual numbers and dual vectors in his research on the geometry of lines and kinematics [1] . He devoted special attention to the representation of directed lines by dual unit vectors and defined the mapping that is known by his name. There exists one-to-one correspondence between the vectors of dual unit sphere 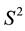 and the directed lines of space of lines
and the directed lines of space of lines . Hence, a differentiable curve on the sphere
. Hence, a differentiable curve on the sphere 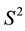 corresponds to a ruled surface in the line space
corresponds to a ruled surface in the line space  [2] - [4] . Ruled surfaces have been widely applied in surface design, manufacturing technology and simulation of rigid bodies [5] .
[2] - [4] . Ruled surfaces have been widely applied in surface design, manufacturing technology and simulation of rigid bodies [5] .
E. Study’s mapping plays a fundamental role in the real and dual Lorentzian spaces [6] . By this mapping, a curve on a dual hyperbolic unit sphere 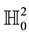 corresponds to a timelike ruled surface in the Lorentzian line space
corresponds to a timelike ruled surface in the Lorentzian line space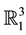 , in other words, there exists a one-to-one correspondence between the geometry of curves on
, in other words, there exists a one-to-one correspondence between the geometry of curves on 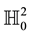 and the geometry of timelike ruled surfaces in
and the geometry of timelike ruled surfaces in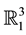 . Similarly, a timelike (spacelike) curve on a dual Lorentzian unit sphere
. Similarly, a timelike (spacelike) curve on a dual Lorentzian unit sphere  corresponds to a spacelike (timelike) ruled surface in the Lorentzian line space
corresponds to a spacelike (timelike) ruled surface in the Lorentzian line space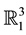 , this means that, there exists a one-to-one correspondence between the geometry of timelike (spacelike) curves on
, this means that, there exists a one-to-one correspondence between the geometry of timelike (spacelike) curves on ![]() and the geometry of spacelike (timelike) ruled surfaces in
and the geometry of spacelike (timelike) ruled surfaces in ![]() [7] . Since the dual Lorentzian metric is indefinite, the angle concept in this space is very interesting. For instance, the dual hyperbolic angle
[7] . Since the dual Lorentzian metric is indefinite, the angle concept in this space is very interesting. For instance, the dual hyperbolic angle ![]() between two dual timelike unit vectors is a dual value formed with the (real) hyperbolic angle
between two dual timelike unit vectors is a dual value formed with the (real) hyperbolic angle ![]() between corresponding two directed timelike lines in the Lorentzian line space
between corresponding two directed timelike lines in the Lorentzian line space ![]() and the shortest Lorentzian distance
and the shortest Lorentzian distance ![]() between these directed timelike lines.
between these directed timelike lines.
Real spherical curvature motion had been introduced by A. Karger and J. Novak [8] . Also, a dual spherical curvature motion has been defined by Z. Yapar [9] . In recent years, study about the real spherical motion has been generalized to the Lorentz spherical motion [6] [7] [10] [11] . In this work, we consider the curvature motion on the dual hyperbolic unit sphere ![]() of the dual Lorentzian space
of the dual Lorentzian space ![]() and the results are carried over to the Lorentzian line space by the E. Study’s mapping.
and the results are carried over to the Lorentzian line space by the E. Study’s mapping.
2. Preliminaries and Definitions
In this section, we give a brief summary of the theory of dual numbers, dual Lorentzian vectors and Study’s mapping.
Let ![]() be the 3-dimensional Minkowski space over the field of real numbers
be the 3-dimensional Minkowski space over the field of real numbers ![]() with the Lorentzian inner product
with the Lorentzian inner product ![]() given by
given by
![]()
where ![]() and
and![]() .
.
A vector ![]() of
of ![]() is said to be timelikeif
is said to be timelikeif![]() , spacelike if
, spacelike if ![]() or
or![]() , and lighlike (null) if
, and lighlike (null) if ![]() and
and![]() .
.
The norm of a vector ![]() is defined by
is defined by![]() . Let
. Let ![]() and
and ![]() be two vec-
be two vec-
tors in![]() , then the Lorentzian cross product of
, then the Lorentzian cross product of ![]() and
and ![]() is given by
is given by
![]()
If ![]() and
and ![]() are real numbers and
are real numbers and![]() , the combination
, the combination ![]() is called a dual number, where
is called a dual number, where ![]() is a dual unit.
is a dual unit.
The set of all dual numbers forms a commutative ring over the real numbers field and is denoted by 𝔻. Then the set
![]()
is a module over the ring 𝔻 which is called a 𝔻-module or dual space. The elements of ![]() are called dual vectors. Thus a dual vector
are called dual vectors. Thus a dual vector ![]() can be written as
can be written as
![]()
where ![]() and
and ![]() are real vectors at
are real vectors at![]() .
.
If ![]() and
and ![]() with
with ![]() then the division is given by
then the division is given by
![]()
Let ![]() be a differentiable function with dual variable
be a differentiable function with dual variable![]() . Then the Maclaurin series generated by
. Then the Maclaurin series generated by ![]() is
is
![]()
where ![]() is the derivative of
is the derivative of![]() . Then it is easy to see that
. Then it is easy to see that
![]()
![]()
![]()
The norm ![]() of a dual number
of a dual number ![]() is defined by
is defined by
![]()
Then we can write
![]()
The Lorentzian inner product of two dual vectors![]() ,
, ![]() is defined by
is defined by
![]()
where ![]() is the Lorentzian inner product of the vectors
is the Lorentzian inner product of the vectors ![]() and
and ![]() in the Minkowski 3-space
in the Minkowski 3-space![]() .
.
A dual vector ![]() is said to be timelike if
is said to be timelike if![]() , spacelike if
, spacelike if ![]() and lightlike (or null) if
and lightlike (or null) if
![]() ,
,
where ![]() is a Lorentzian inner product with signature
is a Lorentzian inner product with signature![]() .
.
The set of all dual Lorentzian vectors is called dual Lorentzian space and it is denoted by
![]()
The Lorentzian cross product of dual vectors ![]() and
and ![]() is defined by
is defined by
![]()
where ![]() is the Lorentzian cross product in
is the Lorentzian cross product in![]() .
.
Lemma 2.1. Let![]() . Then [12]
. Then [12]
1) ![]()
2) ![]() ; and
; and![]() ,
,
3) ![]() ,
,
4) ![]() .
.
Let![]() . Then
. Then ![]() is said to be dual timelike unit vector (resp., dual spacelike unit vector) if the vectors
is said to be dual timelike unit vector (resp., dual spacelike unit vector) if the vectors ![]() and
and ![]() satisfy the following properties:
satisfy the following properties:
![]() , (resp.,
, (resp.,![]() ),
), ![]()
The set of all dual timelike unit vectors (resp., all dual spacelike unit vectors) is called the dual hyperbolic unit sphere (resp., dual Lorentzian unit sphere) and is denoted by ![]() (resp.,
(resp.,![]() ) [6] . (See [13] - [16] for Lorentzian basic concepts.)
) [6] . (See [13] - [16] for Lorentzian basic concepts.)
Theorem 2.2. (E. Study Map) [6] There exists one-to-one correspondence between directed timelike (resp., spacelike) lines of ![]() and an ordered pair of vectors
and an ordered pair of vectors ![]() such that
such that ![]() (resp.,
(resp.,![]() ) and
) and
![]() .
.
Definition 2.1. A directed timelike line in ![]() may be given by two points on it,
may be given by two points on it, ![]() and
and![]() . If
. If ![]() is any non-zero constant, the parametric equation of the line is
is any non-zero constant, the parametric equation of the line is![]() . In this case, the vector given by
. In this case, the vector given by
![]()
is called the moment of the vector ![]() with respect to the origin 0.
with respect to the origin 0.
This means that the direction vector ![]() of the timelike line and its moment vector
of the timelike line and its moment vector ![]() are independent of the choice of the points
are independent of the choice of the points ![]() on the line. However the vector
on the line. However the vector ![]() and
and ![]() are not independent of one another. Also, they satisfy the following properties:
are not independent of one another. Also, they satisfy the following properties:
![]()
Let![]() , 0 and
, 0 and ![]() denote the dual hyperbolic unit sphere, the center of
denote the dual hyperbolic unit sphere, the center of ![]() and the dual orthonormal system at 0, respectively where we have
and the dual orthonormal system at 0, respectively where we have
![]()
![]()
and
![]()
[7] . In this case the orthonormal system ![]() is the system of the space of lines
is the system of the space of lines![]() .
.
A ruled surface is a surface generated by the motion of a straight line in![]() . This line the generator of the surface. This follows the following definition.
. This line the generator of the surface. This follows the following definition.
Definition 2.2. A ruled surface is said to be timelike if the normal of surface at every point is spacelike, and spacelike if the normal of surface at every point is timelike [7] .
Let ![]() and
and ![]() denote two different points at
denote two different points at ![]() and
and ![]() denote the dual hyperbolic angle
denote the dual hyperbolic angle![]() . The hyperbolic angle
. The hyperbolic angle ![]() has a value
has a value ![]() which is a dual number, where
which is a dual number, where ![]() and
and ![]() are the hyperbolic angle and the minimal Lorentzian distance between directed lines
are the hyperbolic angle and the minimal Lorentzian distance between directed lines ![]() and
and![]() , respectively.
, respectively.
3. Dual Curvature Motion on the Dual Hyperbolic Unit Sphere ![]()
Let us consider a fixed dual orthonormal frame ![]() and represent this frame by the dual hyperbolic unit sphere
and represent this frame by the dual hyperbolic unit sphere![]() . Consider the dual hyperbolic spherical motion of a hyperbolic spherical segment
. Consider the dual hyperbolic spherical motion of a hyperbolic spherical segment
![]() of constant such that its endpoints move along circles, one of them being a great circle
of constant such that its endpoints move along circles, one of them being a great circle ![]() which lying on the plane
which lying on the plane ![]() on
on![]() . Let a circle
. Let a circle ![]() with radius
with radius ![]() which is perpendicular to the great circle
which is perpendicular to the great circle
![]() be given in a plane which is parallel to the plane
be given in a plane which is parallel to the plane![]() . Its center is on the vector
. Its center is on the vector ![]() and with distance
and with distance
![]() from the plane
from the plane![]() . The segment
. The segment ![]() moves so that
moves so that![]() . The position vectors of the
. The position vectors of the
endpoints of segment ![]() are chosen as the vectors
are chosen as the vectors ![]() (timelike) and
(timelike) and ![]() (spacelike) of the moving frame
(spacelike) of the moving frame![]() . The vector
. The vector ![]() is then defined by the relation
is then defined by the relation![]() . As the parameter of motion we choose the dual hyperbolic angle
. As the parameter of motion we choose the dual hyperbolic angle ![]() of the timelike vectors
of the timelike vectors ![]() and
and![]() . Let us denote the dual hyperbolic angle of the vectors
. Let us denote the dual hyperbolic angle of the vectors ![]() and
and ![]() by
by![]() . Then
. Then
![]()
where the vector ![]() is spacelike. Further, we have
is spacelike. Further, we have
![]() (
(![]() timelike).
timelike).
where ![]() is timelike. It must be
is timelike. It must be
![]() , i.e.,
, i.e.,
i.e. ![]() or
or![]() , where
, where![]() . Then
. Then![]() . Thus we obtain
. Thus we obtain
![]() (1)
(1)
Thus, we have the orthonormal dual frame![]() . Let this system be represented by moving hyperbolic sphere
. Let this system be represented by moving hyperbolic sphere![]() . Then, a dual hyperbolic curvature motion
. Then, a dual hyperbolic curvature motion ![]() takes place. This motion will be called a dual hyperbolic curvature motion. Let
takes place. This motion will be called a dual hyperbolic curvature motion. Let ![]() be a fixed point on the arc
be a fixed point on the arc![]() . During the dual hyperbolic curvature motion, the point
. During the dual hyperbolic curvature motion, the point ![]() draws an orbit on the fixed hyperbolic sphere
draws an orbit on the fixed hyperbolic sphere![]() .
.
Denote the dual hyperbolic angles of ![]() by
by ![]() and
and ![]() respectively. Then it can be written
respectively. Then it can be written
![]() (2)
(2)
where ![]() [5] . From Equation (2), making the necessary calculations for
[5] . From Equation (2), making the necessary calculations for![]() , we have
, we have
![]() (3)
(3)
![]() (4)
(4)
where ![]() and
and ![]() are the real and dual parts of
are the real and dual parts of![]() , also. Since, Ө1 and Ө2 are constant (i.e.
, also. Since, Ө1 and Ө2 are constant (i.e.![]() ,
, ![]() are all constants),
are all constants), ![]() is constant. Equations (3) and (4) depend only two parameters
is constant. Equations (3) and (4) depend only two parameters ![]() and
and![]() . Thus, Equations (3) and (4) represent a timelike congruence in
. Thus, Equations (3) and (4) represent a timelike congruence in ![]() (for more details on congruences, see [10] [12] ).
(for more details on congruences, see [10] [12] ).
Let ![]() denote the position vector of an arbitrary point
denote the position vector of an arbitrary point ![]() of a directed timelike line of this timelike line congruence in
of a directed timelike line of this timelike line congruence in![]() . Then we have
. Then we have
![]() (5)
(5)
Since ![]() are the coordinates of
are the coordinates of![]() , making the necessary calculations, we obtain
, making the necessary calculations, we obtain
![]() (6)
(6)
![]() (7)
(7)
and
![]() (8)
(8)
If![]() , (i.e.
, (i.e.![]() ) then
) then![]() , i.e.
, i.e.![]() . In this case, from Equation (2) we have
. In this case, from Equation (2) we have![]() . Thus, from Equations (6)-(8) we obtain
. Thus, from Equations (6)-(8) we obtain
![]() (9)
(9)
From Equation (9) we have
![]() (10)
(10)
which represents a line congruence. Thus, we have the following theorem.
Theorem 3.1. During the dual hyperbolic spherical curvature motion ![]() in the case of
in the case of ![]() (hence
(hence![]() ) in Equation (2), the Study map of the orbit which is drawn on the
) in Equation (2), the Study map of the orbit which is drawn on the ![]() by
by ![]() is the congruence in
is the congruence in ![]()
![]() (11)
(11)
If we take ![]() in the Equation (9), then we have
in the Equation (9), then we have
![]() (12)
(12)
Thus, we have the following theorem.
Theorem 3.2. During the dual hyperbolic spherical curvature motion ![]() in the case of
in the case of![]() , the Study map in
, the Study map in ![]() of the orbit drawn on the
of the orbit drawn on the ![]() by
by ![]() is the cone which is given by
is the cone which is given by
![]()
In addition, if we take ![]() (c = constant) then we have
(c = constant) then we have
![]()
which represents a right helicoid.
If![]() , i.e.
, i.e.![]() , then
, then![]() , i.e.
, i.e. ![]() In this case , from Equation (2) we have
In this case , from Equation (2) we have![]() . Thus, from Equations (6)-(8) we obtain
. Thus, from Equations (6)-(8) we obtain
![]() (13)
(13)
If we put![]() , from Equation (13) we have
, from Equation (13) we have
![]() (14)
(14)
From Equation (14) we have
![]() (15)
(15)
which represents a cone whose axis is the vector![]() . Thus, we have the following theorem.
. Thus, we have the following theorem.
Theorem 3.3. During the dual hyperbolic spherical curvature motion, the orbit drawn on ![]() by
by ![]() (if
(if![]() ) represents a cone in the
) represents a cone in the![]() , whose axis is the vector
, whose axis is the vector![]() .
.
If we put![]() , from Equation (13) we have
, from Equation (13) we have
![]() (16)
(16)
From Equation (16) we have
![]() (17)
(17)
which represents a cone whose axis is the vector![]() . Thus, we have the following theorem.
. Thus, we have the following theorem.
Theorem 3.4. During the dual hyperbolic spherical curvature motion, the orbit drawn on ![]() by
by ![]() (if
(if![]() ) represents a cone in the
) represents a cone in the![]() , whose axis is the vector
, whose axis is the vector![]() .
.
4. Analysis of the Orbit of ![]() during the Dual Hyperbolic Spherical Curvature Motion
during the Dual Hyperbolic Spherical Curvature Motion
Seperating real and dual parts of![]() , from Equation (1) we have
, from Equation (1) we have
![]() (18)
(18)
![]() (19)
(19)
Equations (18) and (19) have only two parameters ![]() and
and![]() . Hence Equations (18) and (19) represent a line congruence in
. Hence Equations (18) and (19) represent a line congruence in![]() . Let
. Let ![]() denote the position vector of an arbitrary point
denote the position vector of an arbitrary point ![]() of an oriented line of this congruence in
of an oriented line of this congruence in![]() , then considering Equation (5) we have
, then considering Equation (5) we have
![]() (20)
(20)
Since ![]() are the coordinates of
are the coordinates of![]() , making the necessary calculations, we obtain
, making the necessary calculations, we obtain
![]() (21)
(21)
In the case of ![]() from Equation (21) we have
from Equation (21) we have
![]() (22)
(22)
From Equation (22) we obtain
![]() (23)
(23)
which represents an one-parameter family of cone in![]() .
.
If we put ![]() in the Equation (23), then we have
in the Equation (23), then we have
![]() (24)
(24)
which represents an elliptic cone, whose axis is the vector![]() . Thus, we have the following theorem.
. Thus, we have the following theorem.
Theorem 4.1. During the dual hyperbolic spherical curvature motion, the orbit drawn on ![]() by
by ![]() (if
(if![]() ) represents an elliptic cone, whose axis is the vector
) represents an elliptic cone, whose axis is the vector ![]() in the
in the![]() .
.
In addition, putting various values of parameters in the Equations (21) or (22) we have different line congruences or ruled surfaces in![]() .
.
5. Conclusion
This paper presents the curvature motion on the dual hyperbolic unit sphere![]() . We define the curvature motion on the dual hyperbolic unit sphere
. We define the curvature motion on the dual hyperbolic unit sphere ![]() of the dual Lorentzian space
of the dual Lorentzian space ![]() and the results are carried over to the Lorentzian line space by the E. Study mapping. The orbits drawn on the fixed dual hyperbolic unit sphere by unit dual vectors of an orthonormal base
and the results are carried over to the Lorentzian line space by the E. Study mapping. The orbits drawn on the fixed dual hyperbolic unit sphere by unit dual vectors of an orthonormal base ![]() are obtained. During this carrying, we do an analysis of orbits they drawn by the vectors
are obtained. During this carrying, we do an analysis of orbits they drawn by the vectors ![]() of dual hyperbolic unit sphere and then we get some line congruences, the families of ruled surfaces and ruled surfaces in according to variables of parameters. Moreover we find equations of these line congruences, the families of ruled surfaces and ruled surfaces. This motion and its results may give a way to define new motions and contribute to the study of surface design, manufacturing technology, robotic research and special and general theory of relativity, and many other areas in 3-dimensional Lorentzian space.
of dual hyperbolic unit sphere and then we get some line congruences, the families of ruled surfaces and ruled surfaces in according to variables of parameters. Moreover we find equations of these line congruences, the families of ruled surfaces and ruled surfaces. This motion and its results may give a way to define new motions and contribute to the study of surface design, manufacturing technology, robotic research and special and general theory of relativity, and many other areas in 3-dimensional Lorentzian space.
NOTES
*Corresponding author.