An Integrated Simulation System Based on Digital Human Phantom for 4D Radiation Therapy of Lung Cancer ()
1. Introduction
Respiratory motion hampers the precise delivery of radiation dose to moving targets in radiotherapy of lung cancer [1] . If not properly managed, it can result in insufficient therapeutic dose to the tumor or unnecessary radiation toxicity to surrounding healthy tissues. Tremendous progress has been made in treatment techniques such as respiratory gating [2] [3] , breath-hold/control [4] [5] , and real-time tumor tracking [6] [7] . While recent advances in radiation therapy, especially in four-dimensional (4D) imaging and delivery technologies, show great promise for motion management, they significantly increase treatment complexity and risk of treatment uncertainties. It is thus important to have appropriate tools to validate and evaluate these techniques.
Motion phantoms of different forms have been developed and used to study 4D imaging and 4D radiation dose delivery. These phantoms can be broadly divided into three categories: physical phantom [8] [9] , physiological phantom [10] -[12] , and digital phantom [13] -[16] . Physical phantoms typically consist of mechanical parts to simulate tumor and body anatomy and electrical parts to drive a gear motor with variable velocity. There are a few commercial physical phantoms, such as the Dynamic Thorax Phantom by CIRS (CIRS Inc., Norfork, VA, USA) and the Respiratory Gating platform by Standard Imaging (Standard Imaging Inc., Middleton, WI, USA). The drawback of these types of phantom is that the fabrication can be prohibitively expensive for realistic and widely varying geometrical models among patients. Physiological phantoms are fabricated to simulate the respiratory motion close to the in-vivo condition by explanting natural specimen such as porcine lungs. The lung can be deflated or inflated by a water pump. This enables measurement of anatomical parameters such as surrogate diaphragm position and trajectories of lung lesions, but the lung motion monitoring method employed here is not directly applicable to humans. Overall, the physical and physiological phantoms do not account for patient anatomy and respiratory biomechanics and therefore are sub-optimal for providing guidance for real patient applications.
Digital phantoms are realistic computer based simulations of human respiration that provide a virtual model of patient anatomy and physiology. Imaging data can be generated as if it were from real patients using the accurately computerised model of the physics of the imaging process. Digital phantoms have been used in the research community for developing and testing imaging and treatment techniques. For example, they have been used to improve image quality by compensating for motion in images acquired for diagnostic purposes [17] , treatment planning [18] or image guidance [19] ; to evaluate treatment strategies by simulating the effect of administering them during free breathing [20] [21] ; to evaluate the accuracy of deformable image registration for the prostate and lungs [22] ; and to facilitate development of new imaging and treatment techniques. Among many digital phantoms available in the research community, there is the non-uniform rational B-spline (NURBS)- based 4D digital Extended Cardio Torso (XCAT) phantom [13] [14] . It consists of a whole body model containing the high level anatomical details suitable for application in high resolution imaging modalities such as CT, MRI, and PET. The phantom is capable of simulating human subjects based on gender, age, and size.
The XCAT phantom, together with sophisticated simulation algorithms of 4D imaging and 4D dose calculations, is potentially a unique tool for research and clinical applications for 4D radiation therapy. Patient-specific 4D motion management and optimization in each step of advanced radiation treatment processes can be potentially simulated using the XCAT phantom with clinically acceptable accuracy. It can provide the necessary foundation to establish a robust, clinically feasible framework to apply patient-specific 4D digital phantoms for advanced radiation therapy applications. It is the aim of this work to develop and test a simulation system based on the XCAT phantom for 4D radiation therapy of lung cancer. In this study, an integrated computational simulation program was developed to facilitate the XCAT image generation and manipulation, multi-modality 4D imaging simulation, motion analysis, and 4D dose calculation. To demonstrate the utility of the framework, we tested the program for simulating 4D imaging techniques, particularly 4D-CT and 4D-cone beam CT (CBCT), as well as 4D dose delivery in simulated lung cancer cases. The fully developed system will allow us to improve and develop 4D management techniques for the delivery of accurate and optimal radiation therapy treatments to lung cancer patients.
2. Methods and Materials
2.1. Integrated Computer Program
Radiation therapy of lung cancer is a complex process, involving various imaging techniques at different stages of the process for target volume determination, target localization, motion verification, and treatment assessment. Our goal is to develop a systematic simulation system for characterizing, evaluating, and optimizing advanced radiation therapy of lung cancer based on the XCAT phantom. The key components of this system include simulations of the various imaging techniques, as well as 4D dose delivery.
An integrated computer program was developed in Matlab (R2009a, the Mathworks Inc., Natick, MA) to facilitate the manipulation of the XCAT phantom and the simulation of 4D imaging. Figure 1 shows the graphic user interface (GUI) of the integrated computer program, which consists of the following main functions: 1) Generating, displaying, and converting (to DICOM format) XCAT images. Details about the XCAT phantom can be found in the literature [13] [14] and will not be repeated here; 2) Automatic motion tracking and analysis. Motion tracking was based on a cross-correlation algorithm and was achieved by firstly defining a rectangular region-of-interest (ROI) as a template and then searching the maximal cross-correlative region to the template in the following frames. Motion analysis generates useful information of breathing for motion management: such as breathing variations in amplitude and period, and motion probability distribution; 3) Simulating clinical imaging techniques: such as free-breathing 3D scan, respiratory-correlated 4D-CT and 4D-CBCT.
2.2. Customization of Respiratory Mechanics of the XCAT Phantom
Respiratory mechanics of the XCAT phantom are controlled by two curves: 1) the diaphragm curve not only controls the motion of the diaphragm, but also organs such as the liver, stomach, spleen, and kidneys which all move together at a scaled down magnitude; 2) the chest curve controls the upward and outward rotation of the ribcage to expand the chest. Tumor motion in three orthogonal directions, superior-inferior (SI), anterior-posterior (AP), and medial-lateral (ML), can be controlled separately to follow any specified motion trajectories or just follow the motion of the lungs.
We conducted a study to verify that patient-specific motion trajectories are reproducible with the XCAT
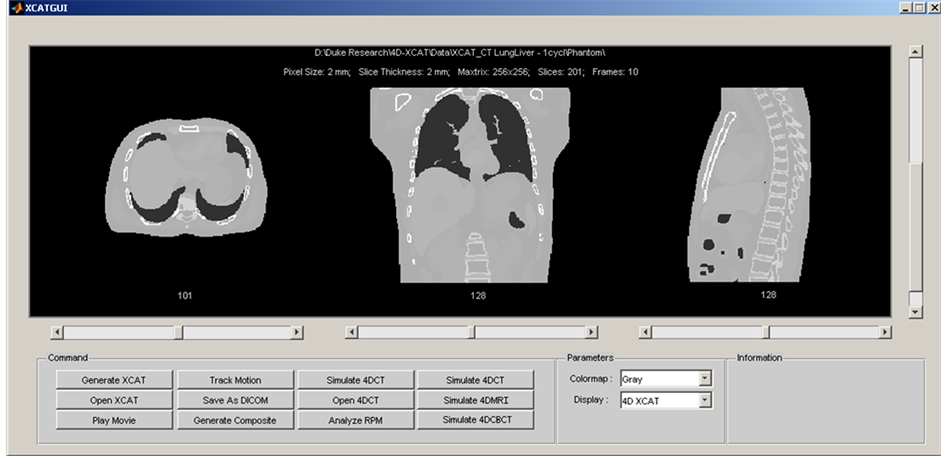
Figure 1. Graphic user interface (GUI) of the integrated computer program of the 4D radiation therapy simulation system.
phantom. In this study, motion trajectories of the diaphragm and chest were extracted from previously acquired MRI scans [23] of five subjects and were imported into the XCAT phantom. Isotropic XCAT images (voxel size: 2 mm) were then generated to follow the input motion trajectories. Motion trajectories of the diaphragm and chest were then measured on the XCAT phantoms using a previously validated automatic motion tracking method [23] [24] . Additionally, the last two subjects (S4 and S5) had lung carcinomas visible in the MRI. Those trajectories were also simultaneously input into the XCAT phantom as the tumor curve for a 2.0 cm spherical tumor placed near the anterior chest wall, about halfway between the diaphragm and apex. The input versus the measured trajectory was compared by calculating the mean absolute difference and standard deviation in motion amplitude.
2.3. Simulation of 4D Imaging
We developed simulation methods based on the XCAT phantom for 4D-CT imaging techniques. The 4D-CT simulation method was adapted from our previously developed algorithm [25] . The simulation process involves virtual scans of 4D-CT carried out entirely on the computer using the XCAT phantoms as the patients. CT scanning parameters (kVp, mA, scan range, number of detector rows, cine time, cine duration, couch movement time, starting respiratory phase, etc.) can be defined in a user-friendly interface. The simulation can then be performed for both regular and irregular breathing patterns. Specifically, the 4D-CT simulation process is carried out in the following steps: 1) User selects a breathing profile and picks a starting point to initiate the 4D-CT image acquisition process; 2) User defines scanning parameters, which include number of slices per rotation, cine time, cine duration, couch movement time, starting and ending slice locations. The XCAT computer program uses these parameters to determine each to-be-acquired image’s corresponding time on the breathing profile, and generate them from a parameter file specifying patient’s anatomic information; 3) With the number of phases to be reconstructed specified by the user, the XCAT computer program will retrospectively sort the images of same couch location into each bin of the phases, according to each image’s corresponding time and relevant location to the automatically-detected peaks on the breathing profile. If multiple or none image exists for a bin, the image of an acquired time nearest to the bin will be selected. Afterwards the sorted images at each phase bin are combined together to compose a whole volume. Upon completion of the above procedures, a 4D-CT dataset of multiple phases will be generated. For this study, the cine-mode 4D-CT images were simulated with the following parameters: kVp: 120; in-plane resolution: 256 × 256, pixel size: 2 mm; slice thickness: 2.5 mm; cine time: 0.5 s; cine duration: 7 s; slices per couch: 16.
We have also developed simulation methods based on the XCAT phantom for 3Dand 4D-cone-beam CT (CBCT). To simulate CBCT scans, XCAT phantom images were first generated with given breathing curves. Cone-beam projections were then generated with the CT-projection function at a frame rate of 11 fps and gantry rotation speed of 3.33˚/sec for 3D-CBCT, and at a frame rate of 2 fps and gantry rotation speed of 0.83˚/sec for 4D-CBCT. For 4D-CBCT, image acquisition parameters, such as gantry rotation speed, frame rate, acquisition time and number of projections acquired, were determined using our previously developed framework for optimized 4D-CBCT imaging [26] . Cone beam projections were then binned into 10 respiratory phases based on phase-sorting. Each bin was subsequently reconstructed with a Feldkamp-type backprojection algorithm.
2.4. Simulation of 4D Dose Delivery
Simulation of 4D dose delivery allows for evaluation of dose that is actually delivered as compared to what is planned. It can be realized on the 4D-XCAT phantom by calculating time-resolved dose deposition at each respiratory phase for each treatment field. To illustrate its feasibility, we simulated the 4D dose delivery process for a typical lung stereotactic-body radiation therapy (SBRT) case in the following steps: 1) 4D XCAT images were generated using the default regular breathing curves (breathing period: 5 s; breathing amplitude: 2 cm; respiratory phases per breathing cycle: 10). A pseudo spherical tumor (diameter = 3 cm) was placed in the middle right lung; 2) Maximum intensity projection (MIP) and average intensity projection (AIP) images were generated from the 10-phase 4D-XCAT images (Phase 0%, 10%, …, 90%), converted to DICOM format, and imported to treatment planning system (EclipseTM, Varian Medical Systems, Palo Alto, CA) for contouring and planning; 3) Internal target volume (ITV) was delineated from the MIP. Planning target volume (PTV) was generated by adding a 5 mm uniform margin to the ITV. Organs at risk (OARs) including lung, heart, spinal cord, and chest wall were contoured in the AIP, which was used for dose calculation; 4) A typical lung SBRT plan was created using 3D conformal technique with eight co-planar treatment fields. The prescription dose of 48 Gy in 4 fractions was designed to provide coverage for 95% of the PTV. Dose constraints to OARs were adapted from Radiation Therapy Oncology Group (RTOG) 0915 protocol. Analytical Anisotropic Algorithm (AAA) was used for dose calculation.
4D dose delivery was simulated by determining the time-resolved dose deposition at each respiratory phase for each treatment beam. Figure 2 shows the workflow of the simulation of real-time 4D dose delivery. Dose rate of 600 MU/min was assumed in the simulation. Final dose distribution was obtained by accumulating dose deposition of all beams and all phases to Phase 0% of the 4D-XCAT phantom via deformable registration using the inherently generated deformation vectors from the XCAT phantom. Dose-volume-histograms (DVHs) of target volumes and OARs were compared between the planned dose and the simulated delivered dose.
3. Results
On average of the 5 subjects, the overall mean (±standard deviation) differences in motion amplitude between the input and measured trajectories was 1.19 (±0.79) mm, which is less than the voxel size of 2 mm. The differences are expected to be even smaller for smaller pixel sizes of the XCAT phantom. Figure 3 shows an example of the comparison between the input and measured trajectories of the tumor for a representative patient for which the XCAT phantom images were generated with voxel size of 1 mm. The mean absolute difference in motion amplitude was 0.3, 0.3, and 0.2 mm, in superior-inferior, anterior-posterior, and medial-lateral directions, respectively.
Figure 4 shows the simulated 10-phase 4D-CT images for a regular respiratory trajectory profile (breathing period: 5 s) (Figure 4(a)) and an irregular respiratory trajectory of a patient (Figure 4(b)). Respiratory motion of the organs and the tumor can be readily seen on both image sets. While there were no apparent motion artifacts for the regular respiratory trajectory, artifacts of disconnected anatomy commonly due to breathing irregularities were seen in certain respiratory phases for the irregular respiratory trajectory. Figure 5 shows an example of the 10-phase bins of a selected 4D-CBCT reconstruction of the XCAT phantom for a regular respiratory trajectory (period: 5 s). Respiratory motion of the tumor was clearly observed in the 4D-CBCT images.
Figure 6 shows the isodose distribution of the delivered 4D dose on the Phase 0% image of the XCAT phantom (Figure 6(a)), the planned dose on the 4DCT-AIP image of the XCAT phantom (Figure 6(b)), and the comparison of DVHs of the different OARs (lungs, cord, esophagus, and heat) and PTV/GTV between the two (Figure 6(c)). Maximum cord dose, maximum esophagus dose, mean heart dose, and V20Gy of the lungs were comparable between the planned dose and delivered dose; the relative differences were 0.3%, 4.0%, 0%, and 2.8%, respectively. 97.5% of the PTV received the prescription dose in delivered dose, as compared to 95% of

Figure 2. Workflow of 4D dose delivery simulation for a lung SBRT case planned using 3D conformal technique.
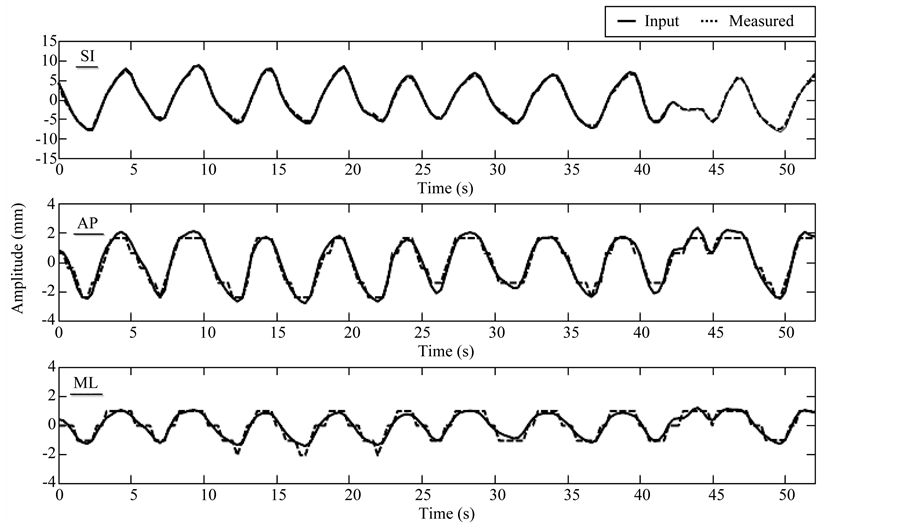
Figure 3. Example of input versus measured trajectories of tumor motion for the XCAT phantom with voxel size of 1 mm. Mean absolute difference in motion amplitude is 0.3, 0.3, and 0.2 mm, in superior-inferior (SI), anterior-posterior (AP), and medial-lateral (ML) directions, respectively. Measurements in AP and ML seem more discrete than the input curves, presumably due to the limited tracking resolution (1 mm, same as the voxel size of the XCAT phantom) for the XCAT images.

Figure 4. Simulated 10-phase 4D-CT images based on the XCAT phantom for a regular breathing profile (a) and for an irregular breathing profile (b). Dotted lines were added to facilitate the visualization of respiratory motion. Red arrows indicate motion artifacts of disconnected anatomy due to breathing irregularity.
the PTV receiving the prescription dose in the plan. These results may indicate that ITV-based lung SBRT planning is a close representation of the actual delivered 4D dose for both target and OARs for regular breathing patterns.
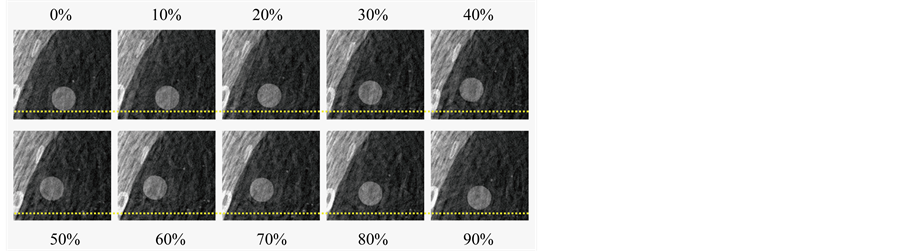
Figure 5. 10 phase bins with a 10% phase window of a selected 4D-CBCT reconstruction of the XCAT phantom with a 5 second respiratory cycle. Dotted lines were added to facilitate the visualization of tumor motion.
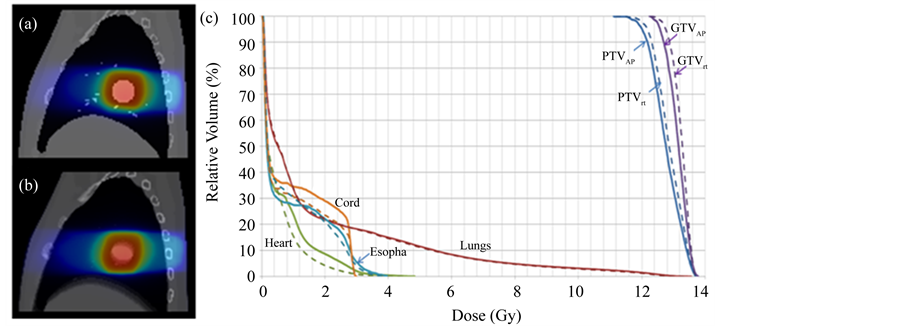
Figure 6. Isodose maps for (a) 4D dose on Phase 0% of the 4D-XCAT; and (b) Planned dose on average intensity projection (AIP) of the XCAT; (c) Comparison of planned DVHs (solid) and 4D dose DVHS (dotted) and delivered dose for different OARs (lungs, cord, esophagus, heart) and PTV/GTV.
4. Discussion
In this study we developed and tested an integrated simulation system based on the XCAT digital human phantom for 4D radiation therapy of lung cancer. We showed that respiratory mechanics of the XCAT phantom can be individualized by incorporating patient-specific breathing trajectories. We have also demonstrated the utility of this system by simulating 4D imaging (4D-CT and 4D-CBCT) and 4D dose delivery. While not shown in this paper, we have also developed simulation methods based on the XCAT phantom for free-breathing 3D CT and CBCT, which are essential components of the current radiation therapy clinical practice. In addition, we have recently employed this simulation system for the development of a novel 4D-MRI technique using internal respiratory surrogates [27] . In that study the XCAT phantom was used to validate the algorithms of respiratory signal extraction and image reconstruction. The capability to conduct computer simulations of 4D imaging and 4D treatment delivery using the XCAT phantom will provide an enhanced insight into the effect of respiratory motion on imaging and radiation dose delivery. This in turn, can lead to new imaging and treatment strategies and modifications of the way breathing is currently handled in radiotherapy. Current 4D techniques are generally based on the assumption that breathing is reproducible [28] [29] , which is largely inaccurate for a majority of real patients. Studies have shown that irregular breathing can produce artifacts and uncertainties in target identification, delineation, and localization, subsequently leading to errors in dose delivery [30] -[33] . Systematic analysis of these effects in well-controlled studies, however, is still lacking in the literature. 4D digital phantoms will allow us to perform controlled studies, in a highly efficient manner, of the effect of respiratory motion on each aspect of 4D motion management techniques, from imaging to dose delivery.
This system can be potentially used to assist clinical decision making in 4D radiation therapy of lung cancer. Accurate, efficient, and robust digital patient respiratory models will be a key component in routine application of safe and efficient 4D methods in radiation therapy planning and delivery. The ability to simulate and evaluate the effect of respiratory motion on imaging and dose delivery in advance will assist the radiation oncologist in the design of optimal treatment plans for a specific patient. There are numerous clinical applications of this simulation system. For example, it can be used to estimate patient-specific uncertainty in the determination of tumor ITV. It has clearly been demonstrated that clinical determination of an ITV based on 4D-CT is prone to error when the patient’s breathing is irregular [34] [35] . We have previously shown that an ITV can be underestimated from 4D-CT by as much as 40%, depending on the patient’s breathing irregularity [25] . Our simulation system can be potentially used to estimate the patient-specific uncertainty in ITV determination associated with 4D-CT imaging.
There are several limitations of the current version of XCAT phantom that have to be considered when employing it for radiation therapy applications. Firstly, the XCAT phantom does not simulate the hysteresis and phase shift effects of the lungs. The average 3D trajectory of the lung lesion in human shows hysteresis-like behaviour, i.e., the lesion follows a path during inhalation that is different from that during exhalation [36] . Phase shifts and organ drifts due to muscle relaxation have been observed [37] , causing different parts of the lungs to reach respiratory peaks at different time points. The lack of the ability to simulate these important properties of lung motion could potentially lead to errors in simulations of 4D imaging and 4D dose delivery. The magnitude of the associated errors remains to be investigated. Secondly, the organs and tissues in the XCAT phantom are modelled homogenously, i.e., same image intensity is assigned to the same organ or sub-organ. As a result, image artifacts and dose calculations due to tissue heterogeneity may not be realistically simulated. In a recent study, Zhong et al. [22] developed numerical phantoms for the prostate and lungs by applying finite element modelling to real patient’s CT images. While these organ-specific digital phantoms inherently embed intensity heterogeneity, which are advantageous for realistic simulations, at the current stage they still lack the integrity and maturity as the XCAT phantom to simulate predicative multi-modality patient imaging data from anatomically diverse subjects. We are currently developing patient-specific XCAT phantoms which will incorporate patients’ actual organ shape/size/intensities and respiratory motion patterns. The fully developed XCAT phantom can lead to more realistic simulation of image techniques and radiation dose deposition. Thirdly, the respiratory biomechanical model of the XCAT phantom may be different from that of real patients. The current model is based on an analysis of sets of respiratory-gated CT data of normal subjects, which represent an averaged motion pattern of a small sampled population. Large variations in respiratory motion have been observed among cancer patients, particularly in lung cancer patients who often have underlying pulmonary diseases. Furthermore, studies have shown that image registration methods which are used to derive motion vectors from CT images could have large uncertainties [38] [39] . Despite the limitations of the XCAT phantom in the current format, our simulation system provides a unique and vital tool for quantitative evaluation of 4D imaging and 4D radiotherapy techniques in a well-controlled setting.
5. Conclusion
In this work, we developed an integrated simulation system based on the XCAT digital phantom and illustrated its utility in 4D radiation therapy of lung cancer. This simulation system is potentially a useful tool for quality control and development of imaging and treatment techniques for 4D radiation therapy of lung cancer.
NOTES
*Corresponding author.