Quantum Field Theory of Graphene with Dynamical Partial Symmetry Breaking ()
Keywords
Graphene, Asymmetric Charged Carriers, Dirac-Hartree-Fock Self-Consistent Field Approximation

1. Introduction
The ongoing boom in experimental researches of graphene is not accompanied, however, by substantial development of nanoelectronic components using its unique properties. The one of the possible reasons of this situation could be the absence of satisfactory description of its electrophysical properties on the basis of quantum field theory.
The ab initio calculations by muffin-tin orbital method and usage of random phase approximation (RPA) for polarization operator to investigate the balance of exchange and correlation interactions on band structure of loosely-packed crystals have shown that strong exchange leads to appearance of an energy gap in the spectrum [1] . Conversely, strong correlation interaction leads to tightening the gap in the band spectrum. The spin nonpolarized ab initio simulations of partial electron densities of two-dimensional graphite have shown that the material is a semiconductor. Interlayer correlations tighten energy gap that results in semi-metal behaviour of threedimensional graphite [1] . The presence of a gap in band spectrum of graphene (at Dirac points ) would increase theoretical estimation of its conductivity to
) would increase theoretical estimation of its conductivity to  that is to value approaching optical (high frequency) conductivity of graphene [1] . But there is a significant discrepancy of theoretical estimates of low-frequency (minimal) conductivity of monolayer graphene [3] -[5] with its experimental value
that is to value approaching optical (high frequency) conductivity of graphene [1] . But there is a significant discrepancy of theoretical estimates of low-frequency (minimal) conductivity of monolayer graphene [3] -[5] with its experimental value  [6] -[12] .
[6] -[12] .
Energy gap ~10 meV can be in spectra of nanostructures with photon-dressed ground state [13] . With measurement accuracy ~1 meV, permissible at the present level of technological development, the gap is not registered [14] , though a sharp change of the Fermi velocity  in Dirac point
in Dirac point , described in Hartree-Fock and RPA [14] , as well as when using the ab initio simulations [15] is the experimental fact [14] .
, described in Hartree-Fock and RPA [14] , as well as when using the ab initio simulations [15] is the experimental fact [14] .
Quantum field theory [16] of pseudo-Dirac quasiparticles [17] -[20] in RPA gives a strong screening which destroys the excitonic pairing instability if dynamic fermion mass  is small in comparison with chemical potential
is small in comparison with chemical potential :
: . The existence of dynamic screening for this system with physical flavor
. The existence of dynamic screening for this system with physical flavor , calculated by Eliashberg self-consistent technique, makes the value of
, calculated by Eliashberg self-consistent technique, makes the value of  non-zero for momentums
non-zero for momentums  [16] . Unfortunately, such a range of values of
[16] . Unfortunately, such a range of values of  also gives practically vanishing mass
also gives practically vanishing mass  for the Fermi momentum
for the Fermi momentum  and Fermi velocity
and Fermi velocity . Additional possible lack of this approach is that though pseudo-Dirac fermions act in 2 + 1 dimensional space-time, an electromagnetic field is defined as usual in 3 + 1 dimensions [2] [16] [21] (otherwise Coulomb interaction in 2D space would be log r rather than needed 1/r).
. Additional possible lack of this approach is that though pseudo-Dirac fermions act in 2 + 1 dimensional space-time, an electromagnetic field is defined as usual in 3 + 1 dimensions [2] [16] [21] (otherwise Coulomb interaction in 2D space would be log r rather than needed 1/r).
In papers [22] -[24] one uses a known analogy between the mass of a particle in the kinetic energy and a factor entered as the mass tensor 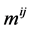 in a quadratic term in the energy expansion of a single-particle state; the magneto-transport term for which there is no such an analogy is discarded. Such description of particles collisions in impurity-free (pure) graphene as electron-phonon scattering gives an estimate of the dynamic conductivity
in a quadratic term in the energy expansion of a single-particle state; the magneto-transport term for which there is no such an analogy is discarded. Such description of particles collisions in impurity-free (pure) graphene as electron-phonon scattering gives an estimate of the dynamic conductivity  at low temperature
at low temperature  [22] -[24] .
[22] -[24] .
In the reference frame where a fermion with nonzero rest mass moves with a velocity , its bispinor wave function
, its bispinor wave function  in addition to non-zero upper components
in addition to non-zero upper components  acquires non-zero lower
acquires non-zero lower
(“positron”) components  [25] [26]
[25] [26]
 (1)
(1)
Changing the light speed  in (1), the pseudo-spinor wave function
in (1), the pseudo-spinor wave function  of quasiparticles in graphene can be written as a sum of electron wave functions (1):
of quasiparticles in graphene can be written as a sum of electron wave functions (1):
 (2)
(2)
where . Due to the process of electron-hole pairs’ production, the current
. Due to the process of electron-hole pairs’ production, the current  [27] oscillates [28]
[27] oscillates [28]
 (3)
(3)
where oscillating summands  are called “Zitterbewegung” terms. Drawback of pseudo-electrodynamics of graphene [28] is the divergence of the expression (2) at
are called “Zitterbewegung” terms. Drawback of pseudo-electrodynamics of graphene [28] is the divergence of the expression (2) at .
.
Weak localization of states can be introduced through non-zero spin-orbit interaction. A possibility of the absence of inversion center for spin-polarized electron density of monolayer grapheme, related with this fact possibility of non-zero spin-orbit contribution , which depends upon
, which depends upon  -component of Pauli matrices vector (spin) and pseudo-Pauli matrices vector (pseudo-spin) and stipulates magnetoelectric effects, has been mentioned in papers [29] -[31] . The phenomenon of spin dependent scattering in non-magnetic graphene can be viewed as an experimentally proven charged carrier asymmetry in graphene [32] [33] . Intrinsic and extrinsic (Rashba) spin-orbit couplings in single layer graphene manifest themselves via the Elliot-Yafet and Dyakonov-Perel disorder-scattering spin-relaxation mechanisms, respectively [34] . The development of quantum spintronic devices is based on spin-dependent bands simulations. These simulations demonstrate that intrinsic spin-orbital interaction is very small, less than 100 meV [35] . Resonant mechanism of the skew scattering, stipulated by increase of the strength of spin-orbital coupling up to ~10 meV in the presence of a metal cluster, has been proposed in [36] . Despite the fact that the non-equilibrium spin can occur in a resonantly acting field (plasmons) of metal cluster near the surface of graphene (the Hanle effect), the presence of such an impurity is also accompanied by the removal of degeneracy of the Dirac cone. The last one leads to the appearance of a hexagon of mini-zones in the vicinity of Dirac cone; respectively, electron-hole asymmetry has another origin which is not related with spin-orbital interaction. In [2] [3] [13] [37] , the conductivity of graphene has been described via the appearance of a gap stipulated by excitonic pairing mechanism and with a value of the same order of magnitude as the aforementioned (induced) one. Besides, the Hall effect is accompanied by intensive process of electron-hole symmetric pair production in the form of “Zitterbewegung” for wave functions [3] [27] [37] . This demonstrates that the “Zitterbewegung” phenomena and the gap of nanostructures with photondressed ground states are capable to neutralize resonant mechanism of the induced skew symmetry.
-component of Pauli matrices vector (spin) and pseudo-Pauli matrices vector (pseudo-spin) and stipulates magnetoelectric effects, has been mentioned in papers [29] -[31] . The phenomenon of spin dependent scattering in non-magnetic graphene can be viewed as an experimentally proven charged carrier asymmetry in graphene [32] [33] . Intrinsic and extrinsic (Rashba) spin-orbit couplings in single layer graphene manifest themselves via the Elliot-Yafet and Dyakonov-Perel disorder-scattering spin-relaxation mechanisms, respectively [34] . The development of quantum spintronic devices is based on spin-dependent bands simulations. These simulations demonstrate that intrinsic spin-orbital interaction is very small, less than 100 meV [35] . Resonant mechanism of the skew scattering, stipulated by increase of the strength of spin-orbital coupling up to ~10 meV in the presence of a metal cluster, has been proposed in [36] . Despite the fact that the non-equilibrium spin can occur in a resonantly acting field (plasmons) of metal cluster near the surface of graphene (the Hanle effect), the presence of such an impurity is also accompanied by the removal of degeneracy of the Dirac cone. The last one leads to the appearance of a hexagon of mini-zones in the vicinity of Dirac cone; respectively, electron-hole asymmetry has another origin which is not related with spin-orbital interaction. In [2] [3] [13] [37] , the conductivity of graphene has been described via the appearance of a gap stipulated by excitonic pairing mechanism and with a value of the same order of magnitude as the aforementioned (induced) one. Besides, the Hall effect is accompanied by intensive process of electron-hole symmetric pair production in the form of “Zitterbewegung” for wave functions [3] [27] [37] . This demonstrates that the “Zitterbewegung” phenomena and the gap of nanostructures with photondressed ground states are capable to neutralize resonant mechanism of the induced skew symmetry.
Electromagnetic interaction between  Dirac particles leads to a renormalization of their masses [38] . On the one hand, this dynamic (renormalized) mass
Dirac particles leads to a renormalization of their masses [38] . On the one hand, this dynamic (renormalized) mass  of charged carriers in graphene should be sufficiently small:
of charged carriers in graphene should be sufficiently small: , to be an agreement with experimental data. On the other hand, the value of
, to be an agreement with experimental data. On the other hand, the value of  should be finite that allows at least getting a match with the experimental value of the dynamic conductivity of graphene [2] [22] .
should be finite that allows at least getting a match with the experimental value of the dynamic conductivity of graphene [2] [22] .
The most promising is the use of Dirac-Hartree-Fock self-consistent field approximation for the description of spin-dependent electrical properties of graphene, since the estimate of dynamic mass of the quasiparticles in graphene in this approximation is given by  [39] .
[39] .
Charged carrier asymmetry in graphene transport experimentally found in [40] [41] by a method [42] , allows assuming non-coincidence of Dirac cone with its replica except for  -point. In the paper [43] , it has been shown that in the flavor model
-point. In the paper [43] , it has been shown that in the flavor model  charged carriers are symmetric as well as the graphene band structure.
charged carriers are symmetric as well as the graphene band structure.
The goal of this paper is to construct a pseudo-bispinor description of graphene, which is based on the DiracHartree-Fock self-consistent field approximation, and to propose a flavor model  for the graphene with spin-polarized sublattices. Coulomb interaction in the model is dynamically screened not due to self-consistent motion of an electron with respect to a hole as in flavor models
for the graphene with spin-polarized sublattices. Coulomb interaction in the model is dynamically screened not due to self-consistent motion of an electron with respect to a hole as in flavor models , but due to self-consistent motion of negatively charged three-particle exciton state relative to positively charged three-particle exciton
, but due to self-consistent motion of negatively charged three-particle exciton state relative to positively charged three-particle exciton .
.
The paper is organized as follows. In Sections 2 and 3 we shortly introduce the approach [39] and use it in a simple tight-binding approximation of the problem and massless case. Section 4 gives explicit expressions for exchange interaction matrices allowing further simulating quantities of interest, which are performed and discussed in Sections 5 and 6; in Section 7 we summarize our findings.
2. The Equations of Self-Consistent Charged Carriers Motion in Graphene
In papers [39] [44] -[46] a new approach has been proposed to describe graphene electronic properties. It utilizes a quasi-relativistic Dirac-Hartree-Fock self-consistent field approximation and assumption on ferromagnetic ordering of the sublattices  (with anti-ferromagnetic ordering of the lattice as a whole). In this approach the graphene is described by the following stationary equation for the second-quantized fermion field
(with anti-ferromagnetic ordering of the lattice as a whole). In this approach the graphene is described by the following stationary equation for the second-quantized fermion field :
:
 (4)
(4)
Here points  in the Brillouin zone of monolayer graphene are designated as
in the Brillouin zone of monolayer graphene are designated as ,
,  is the momentum operator, operator
is the momentum operator, operator  is defined as
is defined as
 (5)
(5)
 is the vector of Pauli matrices, 2D transformation matrices
is the vector of Pauli matrices, 2D transformation matrices  are determined by an exchange interaction term
are determined by an exchange interaction term 
 (6)
(6)
 (7)
(7)
 (8)
(8)
Now, we perform the following non-unitary transformation of the wave function for graphene
 (9)
(9)
In the limit of  we can neglect the mixing of the states for the Dirac points
we can neglect the mixing of the states for the Dirac points  and
and , and get pure two-dimensional case. After this transformation, Equation (4) takes the form similar to a pseudo-Dirac approximation of two-dimensional graphene:
, and get pure two-dimensional case. After this transformation, Equation (4) takes the form similar to a pseudo-Dirac approximation of two-dimensional graphene:
 (10)
(10)
where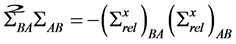 ,
,  ,
,  ,
,  ,
, .
.
In a similar way we can write down the following stationary equation for the second quantized fermion field  on the sublattice
on the sublattice :
:
 (11)
(11)
where ,
,  ,
, .
.
Due to the fact that , the vector
, the vector  of the Dirac cone is somehow rotated and stretched in respect to the vector
of the Dirac cone is somehow rotated and stretched in respect to the vector  of its replica.
of its replica.
3. The Equation of Motion of Massless Charged Carriers in Graphene
Massless approximation of Equation (10) reads
 (12)
(12)
Let wave functions  and
and  with spin up and down respectively has the form
with spin up and down respectively has the form
 (13)
(13)
Bispinor wave functions of quasiparticles moving on the Dirac cones and its replicas can be represented as the free Dirac field of  (pz)-electrons:
(pz)-electrons:
 (14)
(14)
 (15)
(15)
where
 (16)
(16)
is a Bloch function.
In approximation of free  (pz)-electrons all wave functions entering into the expressions (7), (8) are described by the Formulae (14), (15):
(pz)-electrons all wave functions entering into the expressions (7), (8) are described by the Formulae (14), (15):
 (17)
(17)
Then, in this approximation we can write matrices  and
and  without self-action as
without self-action as
 (18)
(18)
 (19)
(19)
It follows from the expressions (18), (19) that the matrices  and
and 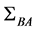 have the form
have the form
 (20)
(20)
 (21)
(21)
Let us find the matrices  and
and  in tight-binding approximation. To do it, we substitute the expression (16) into matrices (20), (21) and calculate integrals entered in elements of these matrices, for example
in tight-binding approximation. To do it, we substitute the expression (16) into matrices (20), (21) and calculate integrals entered in elements of these matrices, for example
 (22)
(22)
Taking into account that the vector difference  lays in
lays in  -th primitive cell:
-th primitive cell: , we transform (22) as
, we transform (22) as
 (23)
(23)
where  -th primitive cell is obtained from the base one by a rotation on an angle
-th primitive cell is obtained from the base one by a rotation on an angle ;
; . Let us account for nearest neighbors only in (23):
. Let us account for nearest neighbors only in (23):
 (24)
(24)
As a basic set we choose  orbitals of
orbitals of  -electrons:
-electrons: 

 . Energy of an electron is not changed with rotation on a lattice vector. Therefore, we can use the symmetry of the problem for simulation simplification by choosing e.g.,
. Energy of an electron is not changed with rotation on a lattice vector. Therefore, we can use the symmetry of the problem for simulation simplification by choosing e.g.,  and
and , as
, as ,
, .
.
4. Partially Broken Symmetry of Model N = 3
Substituting the expression (23) into the matrixes (20), (21) and choosing basic set with , we get in the approximation (24):
, we get in the approximation (24):
 (25)
(25)
 (26)
(26)
Here it was chosen the upper sign for  -orbital
-orbital  and was introduced the following notion
and was introduced the following notion
 . Secular equation with this basic orthogonal set
. Secular equation with this basic orthogonal set  has the form
has the form
 (27)
(27)
Due to the fact that  and the wave function is defined up to a phase multiplier, then Equation (27) is reduced to
and the wave function is defined up to a phase multiplier, then Equation (27) is reduced to
 (28)
(28)
Let us rewrite Equation (28) in momentum representation as
 (29)
(29)
where  owing to momentum conservation law. Then one can obtain
owing to momentum conservation law. Then one can obtain  in an explicit form
in an explicit form
 (30)
(30)
Substituting known expressions for eigenfunctions of hydrogen-like atom [47] and evaluating integrals, we obtain rather lengthy  -dependent invertible matrices, for
-dependent invertible matrices, for  they are pure numeric and up to a common scalar prefactor read
they are pure numeric and up to a common scalar prefactor read
 (31)
(31)
The most interesting thing is that eigenvalue problem (28) gives precisely the known dispersion laws
 , that is problem is persistent up to
, that is problem is persistent up to  variations.
variations.
Now, we take into account higher order in  terms when evaluating
terms when evaluating . Dependence of the Fermi energy
. Dependence of the Fermi energy  on the surface carriers concentration
on the surface carriers concentration  is the replacement of
is the replacement of
 so that
so that . The Fermi energies
. The Fermi energies  and
and
 for electrons and holes, respectively, are represented in Figure 1. One can see that the hole and electron bands are symmetric. Six mini-zones around points
for electrons and holes, respectively, are represented in Figure 1. One can see that the hole and electron bands are symmetric. Six mini-zones around points  of Brillouin zone are also observable in Figure 1.
of Brillouin zone are also observable in Figure 1.
5. Asymmetrical Charged Carriers at Large Fermion Density
Now, let us show that the spectrum  corresponding to Equation (12) can deviate from the conic form at large concentration
corresponding to Equation (12) can deviate from the conic form at large concentration . According to Figure 1, for
. According to Figure 1, for  the Fermi level is in the region with unbroken symmetry of the Dirac cone. When
the Fermi level is in the region with unbroken symmetry of the Dirac cone. When , the Fermi level enters the region with broken symmetry of the Dirac cone. In this region, there is a Fermi energy curve
, the Fermi level enters the region with broken symmetry of the Dirac cone. In this region, there is a Fermi energy curve  which has local hyperbolic points of a “saddle” type. Fermi curves passing through or near these hyperbolic points are local maxima and minima. Since in these points “trajectories” of quasi-particle motion (i.e., the configuration space of the system) are unstable, not all holes (electrons) can reach the Dirac cone (replicas) and annihilate. We demonstrate
which has local hyperbolic points of a “saddle” type. Fermi curves passing through or near these hyperbolic points are local maxima and minima. Since in these points “trajectories” of quasi-particle motion (i.e., the configuration space of the system) are unstable, not all holes (electrons) can reach the Dirac cone (replicas) and annihilate. We demonstrate  surface sections for few
surface sections for few  in Figure 2.
in Figure 2.
Figure 2(a) emphasizes that in the vicinity of Dirac point the cone is persistent due to symmetry (section crosses original cone and its replicas simultaneously), at higher values of , higher order corrections start to contribute. An energy dispersion law for 2D graphene is linear near Dirac cone corner at
, higher order corrections start to contribute. An energy dispersion law for 2D graphene is linear near Dirac cone corner at  (see Figure 2(a)). When section crosses original cone only (Figure 2(b)), we find symmetrical section of the Dirac cone.
(see Figure 2(a)). When section crosses original cone only (Figure 2(b)), we find symmetrical section of the Dirac cone.
Comparing Figure 2(c) with Figure 1 we can conclude that the section of Dirac cone and its replicas at  is placed in one of six mini-zones of the Brillouin zone. It leads to electron-hole asymmetry. Such type of charged carrier asymmetry has been observed in [32] [33] as the resistivity dependence upon direct current at positive and negative values of the gate voltage. We can compare an energy distance between “upper” and “lower” Dirac cones with an energy distance between replicas in section given by the relation
is placed in one of six mini-zones of the Brillouin zone. It leads to electron-hole asymmetry. Such type of charged carrier asymmetry has been observed in [32] [33] as the resistivity dependence upon direct current at positive and negative values of the gate voltage. We can compare an energy distance between “upper” and “lower” Dirac cones with an energy distance between replicas in section given by the relation . In such a section the extremum takes place at
. In such a section the extremum takes place at  (Figure 2(c)). The distance
(Figure 2(c)). The distance  between extrema at
between extrema at  is the distance between nearest upper and lower replicas.
is the distance between nearest upper and lower replicas.  due to rotation of Dirac cone in respect to replicas at
due to rotation of Dirac cone in respect to replicas at .
.
Thus, the six fold rotational symmetry of graphene energy surface near the Dirac point partially breaks, except of Dirac cone’s corner, and, respectively the Dirac cone does not coincide with its replicas.
6. Electron-Hole Localization in the Model N = 3 at Low Carrier Concentration
The displacement of replicas points in the graphene Brillouin zone on respect to the primary Dirac cone points occurs at a distance
 (32)
(32)
Since in the neighborhood of the Dirac cone’s corner , and (as was shown above) the cone persists then, in accord with (32) in the graphene Brillouin zone all points of the Dirac cone replicas shift, except of their corners. To understand what value of the rotation angle it could correspond to, we choose
, and (as was shown above) the cone persists then, in accord with (32) in the graphene Brillouin zone all points of the Dirac cone replicas shift, except of their corners. To understand what value of the rotation angle it could correspond to, we choose  and find
and find  based on (32) and expressions (31) for
based on (32) and expressions (31) for . The rotation angle
. The rotation angle  so it turns out to be a practically right angle
so it turns out to be a practically right angle  where
where ,
,  The last means that the rotation could be large enough for some points in momentum space.
The last means that the rotation could be large enough for some points in momentum space.
Let us find localization regions of non-annihilated quasiparticles. Since momenta  of holes are rotated with respect to the electron momenta
of holes are rotated with respect to the electron momenta  at angle
at angle , the hole Fermi curve
, the hole Fermi curve  is also rotated. Because of the symmetry, the curve
is also rotated. Because of the symmetry, the curve  is effectively rotated at angle
is effectively rotated at angle , as shown in Figure 1. Adding
, as shown in Figure 1. Adding  and the corresponding to it a hole Fermi surface
and the corresponding to it a hole Fermi surface , we find the surface
, we find the surface , which demonstrates charge density distribution at the Fermi level
, which demonstrates charge density distribution at the Fermi level  at low charged carriers concentrations
at low charged carriers concentrations  and is shown in Figure 3.
and is shown in Figure 3.  takes nonzero values outside of Dirac cone’s corner (non-zero values of the chemical potential
takes nonzero values outside of Dirac cone’s corner (non-zero values of the chemical potential ).
).
By virtue of turn of the holes valence band (conduction band electrons) at , the hole liquid is localized so that the electron liquid from its valence band could flow into the vacancies of the hole valence band. Similarly,
, the hole liquid is localized so that the electron liquid from its valence band could flow into the vacancies of the hole valence band. Similarly,

Figure 3. Scheme of localization in flavor model .
.
the hole liquid flows into the vacancies of the valence band electrons at some value . Since the annihilation processes are absent, the hole and electron Fermi levels are not at
. Since the annihilation processes are absent, the hole and electron Fermi levels are not at , and stabilized at some value
, and stabilized at some value and, respectively, the Fermi level is dynamic. Therefore, there is a dynamic overlapping of valence and conduction bands, and, respectively, clear graphene turns out to be a metal. The neighborhood with
and, respectively, the Fermi level is dynamic. Therefore, there is a dynamic overlapping of valence and conduction bands, and, respectively, clear graphene turns out to be a metal. The neighborhood with  is a region where trapped quasiparticles could annihilate; therefore the charged carriers there, are practically absent. This actually is the prohibition for charge carriers to be in the Dirac cone’s corner.
is a region where trapped quasiparticles could annihilate; therefore the charged carriers there, are practically absent. This actually is the prohibition for charge carriers to be in the Dirac cone’s corner.
The formed dynamic equilibrium can be disturbed by injection of carriers  from outside into a forbidden neighborhood
from outside into a forbidden neighborhood . Then, to restore the balance, the charge carriers will move into the forbidden region with subsequent annihilation
. Then, to restore the balance, the charge carriers will move into the forbidden region with subsequent annihilation  and, consequently, having opposite sign free carriers appears in the regions of localization. The energy
and, consequently, having opposite sign free carriers appears in the regions of localization. The energy  of the free carriers is equal to energy of both quanta:
of the free carriers is equal to energy of both quanta: . Since
. Since  is small, the “sea” of free quasiparticles is a shallow one. According to Figure 3, due to hyperbolic points, between basins of electrons and holes there are unstable regions, which leads to disintegration of the large “see” into separate small “puddles”. Such “puddles” are experimentally observed at
is small, the “sea” of free quasiparticles is a shallow one. According to Figure 3, due to hyperbolic points, between basins of electrons and holes there are unstable regions, which leads to disintegration of the large “see” into separate small “puddles”. Such “puddles” are experimentally observed at  [48] .
[48] .
7. Conclusion
The physical flavors approach  to a quantum field description of graphene electronic properties has been developed. It is based on the Dirac-Hartree-Fock self-consistent field approximation and assumption on antiferromagnetic ordering of graphene lattice. The approach is a generalization of the known model
to a quantum field description of graphene electronic properties has been developed. It is based on the Dirac-Hartree-Fock self-consistent field approximation and assumption on antiferromagnetic ordering of graphene lattice. The approach is a generalization of the known model  of massless Dirac fermions in graphene. Its first advantage is that the model
of massless Dirac fermions in graphene. Its first advantage is that the model  gives symmetric electron and hole band structures, which differ from the band structure model
gives symmetric electron and hole band structures, which differ from the band structure model  only by a partial violation of the order of
only by a partial violation of the order of  of the six-fold rotational symmetry of primary Dirac cone and its replicas. In the cone’s corner
of the six-fold rotational symmetry of primary Dirac cone and its replicas. In the cone’s corner  the Dirac cone is degenerated. The second advantage is the possibility to account for charged carriers asymmetry stipulated by exchange interaction potential for different sublattices. The third flavor, given by transformations
the Dirac cone is degenerated. The second advantage is the possibility to account for charged carriers asymmetry stipulated by exchange interaction potential for different sublattices. The third flavor, given by transformations ,
,  , gives charged carriers asymmetry and is expressed in dynamical location of the Fermi level and dynamical localization of electrons and holes.
, gives charged carriers asymmetry and is expressed in dynamical location of the Fermi level and dynamical localization of electrons and holes.