Keywords
Lorentz Transformation, Gravitational Gauge Transformation, Space-Time Structure, Gauge Theory of Gravity, Gravitational Gauge Field

1. Introduction
It is known that, because of the negative results from Michelson-Morley interference experiment [1] and Lodge’s interference experiment [2] [3] , the theory of ether drift is abandoned by physical world. In order to explain these negative experimental results, George Francis Fitzgerald and Hendrik Antoon Lorentz proposed the contraction hypothesis [2] -[6] . In the theory of special relativity, clock dilation effect and ruler contraction effect are natural results of Lorentz transformation. It is known that Lorentz transformation is a mathematical transformation of space-time coordinates of a physical event. From physical point of view, it is only a transformation of the state of an observer. It is known that the state of one observer is independent of the clock and the ruler used by another observer. Why is the time interval between ticks of a clock and the length of a ruler changed under such mathematical transformations? What is the physical mechanism that causes such changes?
Besides in special relativity, clock dilation effect and ruler contraction effect also exist in general relativity [7] -[9] . It is known that, in general relativity, these effects are caused by classical gravity, or say that, they are effects of gravitational interactions. So, there are two kinds of clock dilation effect and ruler contraction effect. One is a kind of kinematical effects in special relativity, and another is a kind of effects of gravitational interactions in general relativity. Is there any relation between these two kinds of effects? In other words, are the underlying physics mechanisms of these two kinds of effects the same? What is the physical nature of the clock dilation effect and the ruler contraction effect caused by Lorentz transformation in special relativity?
Quantum Gauge Theory of Gravity (QGTG) is proposed in 2001 [10] -[13] . The motivation to propose QGTG is try to unify general relativity with quantum theory in the framework of gauge field theory. In 2003, Quantum Gauge General Relativity (QGGR) is proposed in the framework of QGTG [10] -[16] . Unlike Einstein’s general theory of relativity, the cornerstone of QGGR is the gauge principle, not the principle of equivalence, which will cause far-reaching influence to the theory of gravity. In QGGR, the field equation of gravitational gauge field is just the Einstein’s field equation, and in classical level, QGGR returns to Einstein’s general relativity [17] . The field equation of gravitational gauge field in QGGR is equivalent to the Einstein’s field equation in general relativity, so two equations have the same solutions, though mathematical expressions of the two equations are completely different. For classical tests of gravity, QGGR gives out the same theoretical predictions as those of GR [18] -[20] , and for non-relativistic problems, QGGR can return to Newton’s classical theory of gravity [19] . Based on the coupling between the spin of a particle and gravitoelectromagnetic field, the equation of motion of spin can be obtained in QGGR. In post Newtonian approximations, this equation of motion of spin gives out the same results as those of GR [20] . The equation of motion of a spinning test particle in gravitational field can also be obtained [21] . It’s found that this motion deviates from traditional geodesic curve, and the deviation effects are detectable [22] , which is a new classical test of gravity theory. QGGR is a perturbatively renormalizable quantum theory, so based on it, quantum effects of gravity [23] -[26] and gravitational interactions of some basic quantum fields [27] [28] can be explored. Unification of fundamental interactions including gravity can be fulfilled in a semi-direct product gauge group [29] -[32] . If we use the mass generation mechanism which is proposed in [33] [34] , we can propose a new theory on gravity which contains massive graviton and the introduction of massive graviton does not affect the strict local gravitational gauge symmetry of the action and does not affect the traditional long-range gravitational force [35] . The existence of massive graviton will help us to understand the possible origin of dark matter.
In this paper, we first use the language of gauge transformation to formulate Lorentz transformation, and study the change of the structure of physical space-time under this gauge transformation. It will help us to understand the physics behind Lorentz transformation and the nature of Lorentz symmetry.
2. Quantum Gauge Theory of Gravity
A simple introduction on the quantum gauge theory of gravity is given in this chapter. Details on this theory can be found in literatures [10] -[16] . In quantum gauge theory of gravity, the most fundamental physical quantity is gravitational gauge field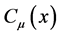 , which is a vector in the corresponding Lie algebra.
, which is a vector in the corresponding Lie algebra.  can be expanded as
can be expanded as
 (1)
(1)
where 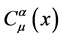 is the component field and
is the component field and  is the generator of global gravitational gauge group.
is the generator of global gravitational gauge group.
The gravitational gauge covariant derivative is given by
 (2)
(2)
where g is the gravitational coupling constant and matrix G is given by
 (3)
(3)
Its inverse matrix is
 (4)
(4)
Using matrix  and
and , we can define two important composite operators
, we can define two important composite operators
 (5)
(5)
 (6)
(6)
Quantum gauge theory of gravity is formulated in absolute space-time [9] [17] . Therefore, in quantum gauge theory of gravity, space-time is always flat and space-time metric is always Minkowski metric, so  and
and  are no longer space-time metric. They are only two composite operators which consist of gravitational gauge field. Einstein’s general relativity is formulated in physical space-time, and
are no longer space-time metric. They are only two composite operators which consist of gravitational gauge field. Einstein’s general relativity is formulated in physical space-time, and 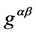 and
and  are metric of physical space-time.
are metric of physical space-time.
The field strength of gravitational gauge field is defined by
 (7)
(7)
where
 (8)
(8)
The Lagrangian of the quantum gauge theory of gravity is selected to be
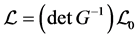 (9)
(9)
where
 (10)
(10)
Its space-time integration gives out the action of the system
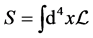 . (11)
. (11)
Under gravitational gauge transformations, the gauge transformation of space-time coordinates is
 (12)
(12)
The gauge transformation of gravitational gauge field is
 (13)
(13)
Using Equation (1), the above relation can be changed into
 (14)
(14)
where 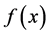 is a function of space-time coordinates which satisfy
is a function of space-time coordinates which satisfy
 (15)
(15)
and 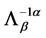 is defined by
is defined by
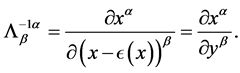 (16)
(16)
3. Relative Space-Time and Absolute Space-Time
The fundamental theory for gravitational interactions can be formulated in two completely different pictures [9] [17] . In one picture, the space-time exists independently, and the structure of space-time is not affected by gravitational field. Like other gauge fields, gravitational field is a physical field which exists and propagates in space-time. This picture is called physical picture of gravity. Classical Newton’s theory of gravity and quantum gauge theory of gravity are set up in this picture. In physical picture of gravity, the space-time is absolute spacetime. In another picture of gravity, the existence of space-time is not independent. The structure of space-time is affected by gravitational field in it. Gravity is only an effect of curved space-time. In this picture, there does not exist a physical gravitational field, and the physics of gravity becomes the geometry of space-time. So, this picture is called geometrical picture of gravity. General relativity is founded in this picture. The space-time in this picture is called relative space-time, or physical space-time.
Two pictures of gravity have completely different transcendental principles, completely different basic physical notions, and completely different mathematical treatment. But for problems of classical gravity, theories of two pictures give out the same theoretical predictions. In other word, for problems of classical gravity, two pictures of gravity are finally equivalent to each other.
In physical picture of gravity, space-time is always flat, so we call it absolute space-time. A coordinate system which is set up in absolute space-time is denoted by , and the space-time coordinate of a physical event is denoted by
, and the space-time coordinate of a physical event is denoted by . The metric of absolute space-time is always the Minkowski metric
. The metric of absolute space-time is always the Minkowski metric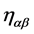 . In geometrical picture of gravity, the space-time is curved when there exists matter in space-time. The space-time in this picture is called relative space-time. In relative space-time, the local clock and ruler are affected by gravitational field. In other words, an observer in absolute space-time observes the clock and ruler used by a local observer in relative space-time, he will find that the time interval between ticks of a clock and the length of a ruler are all changed by gravitational field [9] , though local observer cannot perceive these changes. Suppose that there are two observers in two space-times observe the same physical event. The space-time interval observed by the observer in absolute space-time is denoted by
. In geometrical picture of gravity, the space-time is curved when there exists matter in space-time. The space-time in this picture is called relative space-time. In relative space-time, the local clock and ruler are affected by gravitational field. In other words, an observer in absolute space-time observes the clock and ruler used by a local observer in relative space-time, he will find that the time interval between ticks of a clock and the length of a ruler are all changed by gravitational field [9] , though local observer cannot perceive these changes. Suppose that there are two observers in two space-times observe the same physical event. The space-time interval observed by the observer in absolute space-time is denoted by , and that observed by the local observer in relative space-time is denoted by
, and that observed by the local observer in relative space-time is denoted by . The relation between
. The relation between  and
and  is given by
is given by
 (17)
(17)
The above equation gives out the relation between two space-times.
4. Gravitational Gauge Transformation
Now, let’s study Lorentz transformation. Suppose that we are in absolute space-time. The coordinate system is , and space-time coordinate is denoted by
, and space-time coordinate is denoted by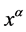 . A global Lorentz transformation is expressed by
. A global Lorentz transformation is expressed by
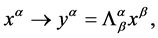 (18)
(18)
where  is the Lorentz transformation matrix. Suppose that the transformation is a boost of the system along the direction of positive x axle with the velocity parameter v, then the transformation matrix is
is the Lorentz transformation matrix. Suppose that the transformation is a boost of the system along the direction of positive x axle with the velocity parameter v, then the transformation matrix is
 (19)
(19)
where  is the rapidity. In this case, the Lorentz transformation (18) becomes
is the rapidity. In this case, the Lorentz transformation (18) becomes
 (20)
(20)
Next, we will study the above Lorentz transformation in the framework of quantum gauge theory of gravity. Gravitational gauge transformation of space-time coordinate is given by Equation (12). Compare Equation (12) with (18), we obtain
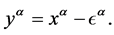 (21)
(21)
Therefore, the gravitational gauge transformation parameter  is
is
 (22)
(22)
It could be seen that the transformation parameter  is a function of space-time coordinate
is a function of space-time coordinate , so the gravitational gauge transformation is a local gauge transformation.
, so the gravitational gauge transformation is a local gauge transformation.
The gravitational gauge transformation of gravitational gauge field  is given by Equation (14). Using Equation (15) and the following relation
is given by Equation (14). Using Equation (15) and the following relation
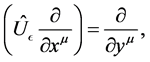 (23)
(23)
we can change Equation (14) into the following form
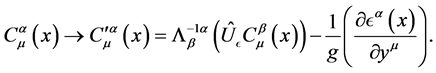 (24)
(24)
Using Equations (16) and (22), the above relation can be changed into
 (25)
(25)
In the above relation, the matrix 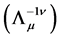 is the inverse matrix of
is the inverse matrix of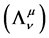 . Its explicit expression is
. Its explicit expression is
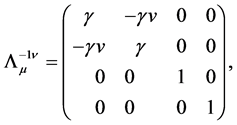 (26)
(26)
It satisfies the following relation
 (27)
(27)
Using above relation, we can change Equation (25) into the following form
 (28)
(28)
Before Lorentz transformation, we are in absolute space-time. Suppose that there is no matter field, and the gravitational field vanishes in all points of space-time. That is
 (29)
(29)
Then, relation (28) is changed into
 (30)
(30)
From above relation, we could see that, after Lorentz transformation, the gravitational field no longer vanishes. There exists constant gravitational field in space-time. Because the gravitational field after Lorentz transformation is constant, its space-time derivative vanishes and the field strength of gravitational gauge field also vanishes. Therefore, there is no gravity in the reference frame after Lorentz transformation, and the reference frame after Lorentz transformation is still an inertial reference frame as expected.
5. Clock Dilation Effect
A basic idea of modern theory on gravity is that the time interval between ticks of a clock and the length of a ruler are all changed by the classical gravitational field, and the structure of physical space-time is also affected by the classical gravitational field. Before Lorentz transformation, the gravitational gauge field vanishes everywhere. But after Lorentz transformation, there exists non-trivial gravitational gauge field which is given by Equation (30). Its explicit form is
 (31)
(31)
Though all matrix elements in gravitational gauge field  are constant, there appear non-zero matrix elements.
are constant, there appear non-zero matrix elements.
Next, let’s study its physical implications. The matrix G which is defined by Equation (3) has the following explicit form
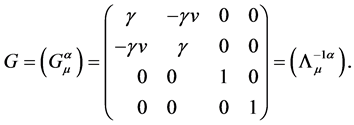 (32)
(32)
Its inverse matrix  is
is
 (33)
(33)
Next, we perform our study in physical space-time. Because the gravitational gauge field vanishes before Lorentz transformation, according to Equation (17), the absolute space-time and the physical space-time are the same. Therefore, before Lorentz transformation, the space-time interval of a physical event can be denoted by , which is just the space-time interval in absolute space-time. After Lorentz transformation, because of the influence of classical gravitational gauge field, the space-time interval of the physical event is changed to
, which is just the space-time interval in absolute space-time. After Lorentz transformation, because of the influence of classical gravitational gauge field, the space-time interval of the physical event is changed to . According to Equation (17), we have
. According to Equation (17), we have
 (34)
(34)
The above relation is the same as that given by Lorentz transformation (18). The above relation is deduced from the point of view of gravitational gauge transformation. It is a relation that is obtained from the change of the space-time structure after gravitational gauge transformation.
Supposed that there is a clock at rest in the reference frame , and the time interval between ticks of the clock is denoted by
, and the time interval between ticks of the clock is denoted by . After Lorentz transformation, the time interval between ticks of the clock is changed to
. After Lorentz transformation, the time interval between ticks of the clock is changed to . According to Equation (34), we have
. According to Equation (34), we have
 (35)
(35)
This is the clock dilation effect given by the change of the gravitational field.
Suppose that there is a ruler that is at rest in the reference frame . The length of the ruler is
. The length of the ruler is . After gauge transformation, we measure the position of the two ends of the ruler at the same time, and obtain the length of the ruler is
. After gauge transformation, we measure the position of the two ends of the ruler at the same time, and obtain the length of the ruler is . According to Equation (34), we have
. According to Equation (34), we have
 (36)
(36)
It is the ruler contraction effect caused by the change of the gravitational gauge field. Relations (35) and (36) are familiar results in special relativity. But here, they are deduced from the viewpoint that the time interval between ticks of a clock and the length of a ruler are all changed when the classical gravitational field is changed.
6. Summary and Discussions
In this paper, the transformation law of vacuum gravitational gauge field and the change of space-time structure under gravitational gauge transformation are studied. It is found that, when the global Lorentz transformation is studied using the method of gravitational gauge transformation, the vacuum gravitational gauge field is changed under the transformation, which will cause the change of space-time structure. The clock dilation effect and the ruler contraction effect are results of the change of space-time structure. It is known that, in special relativity, the Lorentz transformation is only a mathematical transformation of the reference system, or say that it is only a transformation of the moving state of the observer. The change of mathematical parameters of a theory generally can not affect our clock and ruler. In other words, when we change the mathematical parameters of a theory that describe a physical event, the time interval between ticks of a clock and the length of a ruler generally should not be changed accordingly. For a long time, we cannot understand the physical mechanism that causes the change of space-time structure under such mathematical transformation. The goal of this paper is to study such physical mechanism, and we found that the physical mechanism that causes the change of space-time structure under Lorentz transformation is that the change of classical gravitational field causes the change of space-time structure, which is familiar for us in general relativity. In the traditional theories, the picture of the change of the space-time structure in special relativity is completely different from that in general relativity. In special relativity, it is traditionally considered to be an effect of kinematics, and in general relativity, it is considered to be a result of gravity. From the study of this paper, we found that two pictures can be unified, and they are essentially the same. In other words, the clock dilation effect and the ruler contraction effect in special relativity are also effects of gravity. What that the space-time structure is changed by classical gravitational field is a more fundamental law in physics.
It is known that the generalization of special relativity is general relativity, which is a theory of gravity. But, why will the generalization of special relativity which is a kinematical theory inevitably lead to a fundamental theory on gravity? It is hard to understand the physical nature and the inevitability of such generalization just from the point of view of symmetry. Now we know that the physical mechanism that hides behind the Lorentz transformation is gravity and the influence of gravity to space-time structure. It provides us with new insights to understand the essential physical relation between special relativity and general relativity. From physical point of view, the nature of the generalization from special relativity to general relativity is a generalization of gravity, or say that, it is a generalization from the theory of uniform gravitational field to the theory of arbitrary gravitational field.
It is generally believed that the classical gravitational field in inertial reference system should vanish. It is known that, if the initial reference system is inertial, after Lorentz transformation, it is still inertial. According to Equation (31), the classical gravitational field in inertial reference system can be non-zero, and the constant gravitational field can have non-trivial influence to the space-time structure.
The gravitational gauge field after gravitational gauge transformation is given by Equation (31). Using relations (5) and (6), we could calculate the metric of physical space-time. We find that the metric of physical spacetime after Lorentz transformation is still Minkowski metric. So, the gravitational gauge field given by Equation (31) is a solution of the field equation of gravitational gauge field. By the way, we should state that results in this paper cannot be obtained in the traditional formulation of general relativity; for the gravitational field 
 is always zero before and after Lorentz transformation. In the introduction of this paper, we have stated that, for problems of classical gravity, quantum gauge theory of gravity can return to Einstein’s general relativity. Two theories give out the same theoretical predictions on classical tests of gravity. But, we should state here that, for problems of classical gravity, quantum gauge theory of gravity can provide us with more information on gravity and space-time structure than traditional general relativity.
is always zero before and after Lorentz transformation. In the introduction of this paper, we have stated that, for problems of classical gravity, quantum gauge theory of gravity can return to Einstein’s general relativity. Two theories give out the same theoretical predictions on classical tests of gravity. But, we should state here that, for problems of classical gravity, quantum gauge theory of gravity can provide us with more information on gravity and space-time structure than traditional general relativity.
Equation (17) gives out important relation between two space-times. It is known that the structure of absolute space-time is fixed; it cannot be changed by any man-made machine. But with the guide of Equation (17), it is possible for us to change local structure of physical space-time, which will have far reaching influence on human kinds; for example, we can make a machine that can essentially prolong human being’s life by physical method. Details on this topic can be found in [9] . We will not repeat it here.