Forced Convection Thermal Boundary Layer Transfer for Non-Isothermal Surfaces Using the Modified Merk Series ()
1. Introduction
Heat transfer in Newtonian fluids from external surfaces of bodies of various geometries has been the subject of numerous investigations during the past decades, since the pioneer work of Prandtl [1] [2] [3] . The interest in this subject still continues. However, in most of the works it has been assumed that the flow is over isothermal surfaces. In practice, it is sometimes found that the non-isothermal surface case is important because the isothermal case does not occur naturally. The present work is done to provide a theoretical means of analyzing the momentum and energy transport in such flows. The Merk-Chao-Fagbenle series solution technique is employed in this work, so a brief history of the method is appropriate.
A procedure which belongs to the category of “wedge” methods and which provides a rigorous refinement of the local similarity concept is that of Merk [4] . Following Gortler and Meksyn [5] [6] , Merk derived the momentum and energy boundary layer equations in the transformed coordinates . In common with Gortler method, his series solution is also expressed in terms of universal functions. The point of departure is that Gortler expanded the “wedge” variable or the pressure gradient
. In common with Gortler method, his series solution is also expressed in terms of universal functions. The point of departure is that Gortler expanded the “wedge” variable or the pressure gradient  in series of
in series of  while Merk chose the inverse expansion and adopted
while Merk chose the inverse expansion and adopted  as one of the independent coordinates. Merk evaluated the first term in the series by the asymptotic integration method propounded by Meksyn. As in Gortler’s series, the first term corresponds to the local similarity solution. Merks method is an extension or refinement of Meksyn’s procedure. An essential feature of Merk’s scheme is that it makes possible rapid calculations of the significant boundary layer quantities with the aid of a limited number of universal functions which can be tabulated once and for all [7] [8] .
as one of the independent coordinates. Merk evaluated the first term in the series by the asymptotic integration method propounded by Meksyn. As in Gortler’s series, the first term corresponds to the local similarity solution. Merks method is an extension or refinement of Meksyn’s procedure. An essential feature of Merk’s scheme is that it makes possible rapid calculations of the significant boundary layer quantities with the aid of a limited number of universal functions which can be tabulated once and for all [7] [8] .
An advance in the accuracy of boundary-layer series solutions was therefore made possible by Merk in 1959. He refined the “wedge method” proposed by Meksyn by choosing to treat the wedge parameter,  as an independent variable rather than the stream wise coordinate,
as an independent variable rather than the stream wise coordinate, . Thus the Merk series were expanded about the local similarity solution rather than the forward stagnation point of the body, as had been the convention in the past [5] [6] . However, an error in the form of series presented by Merk was found by independent researchers [7] [8] . Chao and Fagbenle therefore put forth a corrected form of Merk’s series and use it to perform a universal, laminar boundary layer analysis for the forced flow of Newtonian fluids over isothermal bodies. Since then, the Merk-Chao-Fagbenle’s approach has been used with success for a family of boundary-layer solutions.
. Thus the Merk series were expanded about the local similarity solution rather than the forward stagnation point of the body, as had been the convention in the past [5] [6] . However, an error in the form of series presented by Merk was found by independent researchers [7] [8] . Chao and Fagbenle therefore put forth a corrected form of Merk’s series and use it to perform a universal, laminar boundary layer analysis for the forced flow of Newtonian fluids over isothermal bodies. Since then, the Merk-Chao-Fagbenle’s approach has been used with success for a family of boundary-layer solutions.
Some of the latest applications of the Merk-Chao-Fagbenle series solution technique have been universal boundary layer analyses of the mixed convection to Newtonian fluids by Cameron, M.R. et al. [9] and the pureforced and pure natural convection to non-Newtonian power-law fluids also by Cameron, M.R. et al. [10] . Meissner, D.L. et al. [11] extended the Merk-Chao-Fagbenle method to mixed convection to power-law fluids. Tien-Chen, A.C. et al. [12] applied the method to natural convection to power-law fluids from two-dimensional or axisymmetrical bodies of arbitrary contour. Falana, A. [13] [14] also applied the method for the analysis of thermal boundary layer for non-isothermal cases of flat plate and horizontal cylinder in cross flow.
The purpose of the present investigation is to employ the Merk-Chao-Fagbenle procedure for the analysis of thermal boundary layer on non-isothermal surfaces by providing firstly the sequence of the differential equations governing the universal functions associated with the method and, secondly, to provide a tabulation of these and other related functions.
With the availability of such tabulation, the determination of the local wall shear and the surface heat transfer rates over the non-isothermal simple geometrical surfaces become a simple matter, once the outer stream velocity distribution is known. The development of the boundary layer and details of the velocity and temperature fields can be obtained with equal ease.
2. Governing Equations and Mathematical Analysis
Here, consideration is given to the conservation equations for steady, laminar, non-dissipative, constant property boundary layer flow over two-dimensional or rotationally symmetrical (or axisymmetric) bodies of non-uniform surface temperature,  , situated in an infinite ambient fluid of undisturbed temperature,
, situated in an infinite ambient fluid of undisturbed temperature, . The coordinate
. The coordinate  denotes the distance along the body surface from the forward stagnation point, and the coordinate
denotes the distance along the body surface from the forward stagnation point, and the coordinate  denotes the normal distance from the surface. Accordingly, the velocity components
denotes the normal distance from the surface. Accordingly, the velocity components  and
and 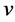 are in
are in  and
and 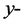 directions respectively. For axisymmetric flows,
directions respectively. For axisymmetric flows,  represents the distance from the axis of symmetry to the body surface, and for two-dimensional flows,
represents the distance from the axis of symmetry to the body surface, and for two-dimensional flows,  , the reference length. Following Chao and Fagbenle, the boundary layer equations are reproduced below:
, the reference length. Following Chao and Fagbenle, the boundary layer equations are reproduced below:
 (1)
(1)
 (2)
(2)
 (3)
(3)
The boundary conditions considered by Merk-Chao-Fagbenle are,
 (4)
(4)
 (5)
(5)
where 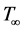 is a constant.
is a constant.
The continuity equation is identically satisfied by introducing a stream function 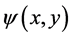 defined by
defined by
 (6)
(6)
In (6) and other equations which follow, one needs only to set  for two-dimensional flows.
for two-dimensional flows.
Following Chao and Fagbenle, the 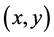 coordinate system is transformed into a new dimensionless coordinate system by adopting the dimensionless variables.
coordinate system is transformed into a new dimensionless coordinate system by adopting the dimensionless variables.
 (7)
(7)
A dimensionless stream function f is introduced, such that
 (8)
(8)
From (6), (7) and (8), we obtain
 (9a)
(9a)
 (9b)
(9b)
where
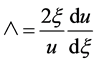 (10)
(10)
is the wedge variable.
It was named by Go rtler as the principal function.
Using (9) in (1), the momentum equation with associated boundary conditions may be reduced to the following system:
 (11)
(11)
and the boundary conditions are
 (12)
(12)
The primes denote differentiation with respect to 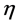 while
while 
The quantity  is a function of
is a function of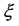 , i.e. x can be calculated explicitly if U(x) is given.
, i.e. x can be calculated explicitly if U(x) is given.
The above momentum Equation (11) is unchanged for the uniform surface temperature problem.
In order to transform Equation (3), we write
 (13)
(13)
The boundary conditions are:
For  and
and
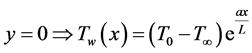 (14)
(14)
For
 and
and  (15)
(15)
The dimensionless temperature is defined as:
 (16)
(16)
Substituting (13) in (16), gives
 (17)
(17)
Making use of (9) and (17) the transformation of (3) is now easily obtained as
 (18)
(18)
while the boundary conditions (4) and (5) become:
 (19)
(19)
The temperature parameter, 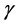 is given by
is given by

 (20)
(20)
It can now be seen that with the variable wall temperature proposed in (13), Equation (18) contains an additional term:

With  = constant, Equation (18) reduces to the same equation considered by Chao and Fagbenle.
= constant, Equation (18) reduces to the same equation considered by Chao and Fagbenle.
Herewith, the transformations are complete and we have now to solve (11) with boundary conditions (12) and (18) with boundary conditions (19).
3. Solution Methodology
The appropriate series solution for (11) and (12) is that used by Chao and Fagbenle. It is given by
 (21a)
(21a)
The appropriate series solution for (18) and (19) according to Chao and Fagbenle is stated as follows:
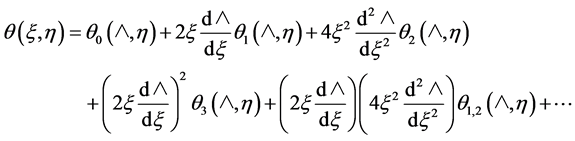 (21b)
(21b)
Upon substituting (21a) into (11) and (12) and collecting terms, free of  and then terms common to
and then terms common to
 ,
,  etc, leads to the following hierarchy of differential equations:
etc, leads to the following hierarchy of differential equations:
 (22)
(22)
 (23)
(23)
 (24)
(24)
An inspection of the above set of equations shows that they can be integrated as if they were ordinary differential equations since, for any given stream wise location,  is fixed. Furthermore, all
is fixed. Furthermore, all 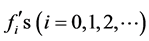 are universal in the sense that they depend on a single parameter. As such, they can be tabulated once and for all.
are universal in the sense that they depend on a single parameter. As such, they can be tabulated once and for all.
For energy Equations (18) and (19), series (21b) leads to hierarchy of differential equations which depends on 3 parameters Pr,  and
and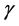 . It is rather too bulky to tabulate the resulting universal functions.
. It is rather too bulky to tabulate the resulting universal functions.
We seek a better series solution for (18) and (19). A better series solution which leads to only a 2-parameter universal functions dependence is:
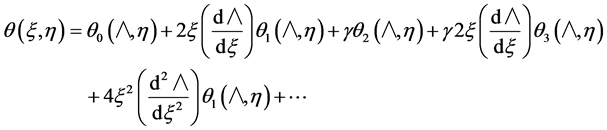 (26)
(26)
Substituting (26) in (18) and (19) leads to the following hierarchy of differential equations:
 (27)
(27)
 (28)
(28)
 (29)
(29)
 (30)
(30)
 (31)
(31)
With boundary conditions:
for  and for
and for 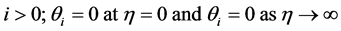 (32)
(32)
Thus all the temperature functions in the sequence dependent on 2 parameters,  and
and .
.
The dependence of the temperature functions on the temperature parameter  is indirect through the series solution expansion. This parameter
is indirect through the series solution expansion. This parameter  would only need to be evaluated at each point of the flow and does not come into the tabulation of the universal functions.
would only need to be evaluated at each point of the flow and does not come into the tabulation of the universal functions.
With the form of the modified Mark-Chao-Fagbenle series proposed in Equations (21), (26), the higher-order solutions depend on the lower-order solutions, but not vice-versa. An inspection of the resulting equations also shows that there are no terms containing the derivatives of the parameter  and therefore, the geometry of the surface is totally absorbed in these parameters. By assigning a fixed value of
and therefore, the geometry of the surface is totally absorbed in these parameters. By assigning a fixed value of  for any given streamwise location, the equations can be integrated as if they were ordinary differential equations and the results tabulated once and for all.
for any given streamwise location, the equations can be integrated as if they were ordinary differential equations and the results tabulated once and for all.
When the solutions for the various ’s and
’s and ’s are available, the parameters of physical interest for the present problem which can readily be obtained are the local skin friction coefficient
’s are available, the parameters of physical interest for the present problem which can readily be obtained are the local skin friction coefficient , displacement and momentum thickness, local Nusselt number, etc.
, displacement and momentum thickness, local Nusselt number, etc.
The local Nusselt number may be defined by

and one finds, after transformation
 (33)
(33)
Chao and Fagbenle [7] [8] have already given extensive applications to the calculation of the local friction coefficient, displacement and momentum thickness. Tabulated values of the above mentioned functions are available with the authors. However, we shall confine ourselves here to the calculation of the local heat transfer quantities.
The  and the
and the  functions
functions  are universal in character. The
are universal in character. The  functions depend on the single parameter
functions depend on the single parameter 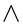 while the
while the 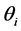 functions depend, additionally, on Pr. They are tabulated once and for all. Equations (22) to (31) with their respective boundary conditions therefore use the above technique. The governing ordinary differential equations for the
functions depend, additionally, on Pr. They are tabulated once and for all. Equations (22) to (31) with their respective boundary conditions therefore use the above technique. The governing ordinary differential equations for the  and the
and the  functions are integrated sequentially using the fourth order Runge-Kutta method.
functions are integrated sequentially using the fourth order Runge-Kutta method.
We first convert the equations stated above into the following simultaneous linear equations of first order as follows.
 (34)
(34)
Then the Newtons method is applied to transform the problem into initial value one, where the initial conditions are:
 (35)
(35)
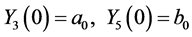 (36)
(36)
Hence,  and
and  are a priori unknown and has to be determined as part of the numerical solution. Once the problem is reduced to initial value problem, it is solved using the famous fourth-order Runge-Kutta method.
are a priori unknown and has to be determined as part of the numerical solution. Once the problem is reduced to initial value problem, it is solved using the famous fourth-order Runge-Kutta method.
A computer program was written for the calculation of  for 20 values of
for 20 values of  in the range
in the range . According to Chao and Fagbenle the selection of the lower limit is based on the anticipation that the Merk-Meksyn procedure is, in general, not applicable to regions of retarded flow near the separation point at which
. According to Chao and Fagbenle the selection of the lower limit is based on the anticipation that the Merk-Meksyn procedure is, in general, not applicable to regions of retarded flow near the separation point at which .
.
The computation began with . Since
. Since  was unknown, Newton’s iterative scheme was used starting from a guessed value of
was unknown, Newton’s iterative scheme was used starting from a guessed value of  say
say . Any reasonable initial guess would eventually lead to the desired result.
. Any reasonable initial guess would eventually lead to the desired result.
Very high accuracy is required of the basic function  and its derivatives since
and its derivatives since  and hence, other functions of the higher order in the hierarchy of the differential equations are sensitive to its variation. The fact is that the differential equation for
and hence, other functions of the higher order in the hierarchy of the differential equations are sensitive to its variation. The fact is that the differential equation for  contains derivatives of
contains derivatives of  and
and  with respect to
with respect to . After a number of trials, the integration step size used is:
. After a number of trials, the integration step size used is:  for
for .
.
The iteration was to continue until the following conditions was met:
 (37)
(37)
where  designates or represents some maximum large value of
designates or represents some maximum large value of .
.
The results obtained (for the similarity equations) as a result agreed with the published data of Chao and Fagbenle within very close limits for all ’s investigated. This is demonstrated in Table1
’s investigated. This is demonstrated in Table1
The integration of the 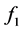 equation requires the evaluation of the derivatives
equation requires the evaluation of the derivatives  and
and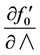 .
.
A method of parameter differentiation was employed for the evaluation of these derivatives.
The integration of the  equation was done easily since it does not involve the
equation was done easily since it does not involve the 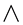 -derivatives. For the
-derivatives. For the 
equation, the evaluation of the derivatives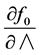 ,
,  ,
,  and
and  was also carried out using the method of parameter differentiation.
was also carried out using the method of parameter differentiation.
The integration step size 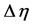 used in numerical computation of the
used in numerical computation of the , (for
, (for ) were the same as those for
) were the same as those for .
.
The above choice of  led to wall derivatives of the
led to wall derivatives of the 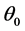 function which are accurate to six significant figures, based on a comparison with the already cited work of Chao and Fagbenle. This is equally demonstrated in Table2
function which are accurate to six significant figures, based on a comparison with the already cited work of Chao and Fagbenle. This is equally demonstrated in Table2
The iterative routine for the computation of  is essentially the same as that for the
is essentially the same as that for the  function.
function.

Table 1. Wall derivatives of universal velocity functions .
.

Table 2. Wall derivatives of temperature function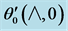 ,
, .
.
3.1. Accuracy of the Numerical Program
We can actually assess the accuracy of the present numerical program for the two basic functions  and
and  by comparing the results deduced from it with known accurate results. The data of Chao and Fagbenle [7] [8] is used since they are (obtained) accurate to twelve significant figures.
by comparing the results deduced from it with known accurate results. The data of Chao and Fagbenle [7] [8] is used since they are (obtained) accurate to twelve significant figures.
It is seen that for the entire range of  used, there is almost complete agreement between the present work for
used, there is almost complete agreement between the present work for  and those of Chao and Fagbenle up to six significant figures (Table 1).
and those of Chao and Fagbenle up to six significant figures (Table 1).
Computed values of  for all combinations of
for all combinations of  and
and  used also shows excellent agreement with the Chao and Fagbenle data (Table 2). These tables show that the present numerical program is capable of producing very accurate data for the two basic functions
used also shows excellent agreement with the Chao and Fagbenle data (Table 2). These tables show that the present numerical program is capable of producing very accurate data for the two basic functions 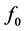 and
and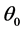 .
.
3.2. Tabulation of Significant Wall Derivatives and Other Relevant Functions
Computer printouts of the velocity functions  and
and  for
for 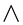 ranging from −0.15 to 1.0 and those of the temperature functions
ranging from −0.15 to 1.0 and those of the temperature functions 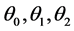 and
and  for the same range of
for the same range of  and for Prandtl numbers
and for Prandtl numbers  and 100.0 are available but are too bulky to be included in this paper.
and 100.0 are available but are too bulky to be included in this paper.
In design and other technological applications, it is, in most cases, the surface characteristics, such as the local frictional drag and the heat and mass transfer coefficients, which are of interest. The prediction of these quantities requires only the information on the wall derivatives:

It should be emphasized that the Merk-Chao-Fagbenle’s method as employed in this work is strictly applicable to incompressible, uniform property laminar boundary layer flows.
Since all tabulated data are available for various values of  it is convenient to plot
it is convenient to plot  and
and  versus
versus  and determine the values of
and determine the values of  and
and  corresponding to these values of
corresponding to these values of  given in the tables.
given in the tables.
At the forward stagnation point, 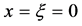 and
and 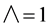 or
or , corresponding respectively to the two-dimensional or axisymmetrical boundary layers.
, corresponding respectively to the two-dimensional or axisymmetrical boundary layers.
With the aid of the universal functions the local heat (or mass) transfer coefficient can be obtained as follows:
 (38)
(38)
where
 (39)
(39)
and
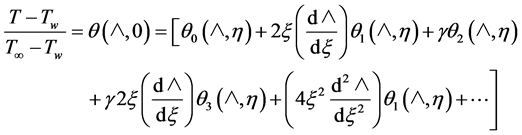 (40)
(40)
for various values of the Prandt number.
The universal functions ’s depend on the Pradtl number as a parameter.
’s depend on the Pradtl number as a parameter.
4. Conclusion
The Chao and Fagbenle’s modification of Merk series was employed for the analysis of forced convection thermal boundary layer transfer for non-isothermal surfaces. The sequence of the differential equations governing the universal functions associated with the method has been presented together with the tabulation of these functions.
Nomenclature
D—Diameter of circular cylinder
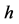 —Local heat transfer coefficient
—Local heat transfer coefficient
 —Thermal conductivity L—Reference length Nu —Nusselt number defined in Equation (38)
—Thermal conductivity L—Reference length Nu —Nusselt number defined in Equation (38)
Pr—Prandtl number R—Radial distance from a surface element to the axis of a rotationally symmetrical body Re—Reynolds number appropriately defined where used T—Temperature
 —Velocity component in x-direction
—Velocity component in x-direction
 —Velocity at outer edge of boundary layer
—Velocity at outer edge of boundary layer
 —Velocity component in Y-direction
—Velocity component in Y-direction
 —Stream wise co-ordinate measured along surface from front stagnation point
—Stream wise co-ordinate measured along surface from front stagnation point
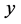 —Co-ordinate normal to surface
—Co-ordinate normal to surface
 —Thermal diffusivity
—Thermal diffusivity
 —Dimensionless co-ordinate defined in Equation (7)
—Dimensionless co-ordinate defined in Equation (7)
 —Wedge variable defined in Equation (10)
—Wedge variable defined in Equation (10)
 —Dynamic viscosity
—Dynamic viscosity
 —Dimensionless co-ordinate defined in Equation (7)
—Dimensionless co-ordinate defined in Equation (7)
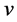 —Kinematic viscosity
—Kinematic viscosity
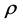 —Mass density
—Mass density
 —Shear stress at wall
—Shear stress at wall
 —Temperature parameter defined in Equation (20)
—Temperature parameter defined in Equation (20)
Subscript
 —Wall condition
—Wall condition
∞—Free stream condition Other symbols are defined in the text.
NOTES
*Corresponding author.