1. Introduction
The classical game theory emerged from the work of Von Neumann [1] , and is applied to various fields, such as economics, social science, medical science, biology and physics [2] -[4] . The relationship of the mathematical game theory and the sources of quantum entanglement was first reported in 1999 by David Meyer [5] . In the same year, Eisert and his coworkers proposed the quantization of nonzero sum games, and exploited the quantized scheme into studying Prisoners’ Dilemma as a particular case of game [6] . From then on the interested physicists have strenuously studied the field that is taken to be a completely new direction in quantum correlations and quantum computation processing. The original protocol for  quantum games was introduced by Eisert et al. through quantum entanglement [6] [7] . In the seminal paper of Meyer [5] and a number of subsequent papers [8] -[13] a particular two-parameter subset of SU(2) is introduced as the strategic space for the players, which has mathematical simplicity and can solve some of the dilemmas of classical game theory.
quantum games was introduced by Eisert et al. through quantum entanglement [6] [7] . In the seminal paper of Meyer [5] and a number of subsequent papers [8] -[13] a particular two-parameter subset of SU(2) is introduced as the strategic space for the players, which has mathematical simplicity and can solve some of the dilemmas of classical game theory.
The quantum entanglement between spatially separated parties is the powerful source of processing the quantum information and the quantum computation. At present, the behavior of quantum entanglement in relativistic setup is under exploration [14] -[17] and some fascinating conclusions have been received. The undergoing studies in the noninertial frames show that entanglement between different modes of various field is degraded by the Unruh effect and the degree of entanglement asymptotically attains a non-vanishing minimum value in the infinite acceleration. Recently, the relativistic setup has been applied to the study of quantum game in noninertial frame and some interesting results have been gained in references [18] -[20] . On the quantum Prisoner’s Dilemma, for instance, S. Khan and M. K. Khan show that the payoff functions of the players are strongly affected by the acceleration of the noninertial frame and the symmetry of the game is disturbed in some extent [18] . Furthermore, quantum Stackelberg Duopoly in a Noninertial frame has been investigated and found that benefit of the initial state entanglement in the quantum form of the duopoly in the initial frame is adversely influenced by the acceleration of the non-stationary player [19] . Some theorists generalized the quantum game for three players, which one of the players stays stationary and the two others move with a uniform acceleration [21] .
Quantum game theorists have studied various specific games, such as Prisoner’s Dilemma, Battle of the Sexes, Cournot duopoly, Stackelberg Duopoly, and symmetric games like Rock-Paper-Scissors and so on [8] -[13] and [18] -[20] and [22] -[24] . Researchers intended to find solutions to those classical game in the background of quantum entanglement. Here, the word solution refers to a set of strategies that the rational players will surely play [22] .
In this Letter, we study the influence of the Unruh effect on the payoff functions of the players in the Battle of Sexes. We find that the game in noninertial frame can be transformed to classical game when the initial state is unentangled and both players remain stationary (i.e. acceleration is zero). We show that the expected payoffs of both players are relevant not only to the probability distributions of the players and the degree of entanglement of the initial state but they also vary with the acceleration of the moving player.
2. Quantum Version of Battle of the Sexes in Noninertial Frame
We exploit the concepts of quantum games in noninertial frame to study a two-person static game of complete information, which is called the Battle of the Sexes. The game is usually described as the following exposition: A women, Alice, and a man, Bob, are planning to decide where to spend the Saturday night: Alice would prefer to attend the Ballet, while Bob would like to watch the football match at the television. They would prefer to stay together rather than far apart. We can represent the game in a normal form by denoting by B (Ballet) and F (Football) the two pure strategies which constitutes the common strategic space . The game is represented by the payoff matrix in the table 1.
. The game is represented by the payoff matrix in the table 1.
2.1. Quantization Scheme
In order to quantize the classical strategies B and F for player Alice, we assigned two basic vectors  and
and  in a Hilbert space of two-level system to B and F, respectively [6] . Similarly quantization scheme can be applied to the strategies of player Bob and we obtain the quantum formation of the payoff table in the table 2.
in a Hilbert space of two-level system to B and F, respectively [6] . Similarly quantization scheme can be applied to the strategies of player Bob and we obtain the quantum formation of the payoff table in the table 2.
2.2. The Quantum Game in Noninertial Frame
We consider that Alice and Bob share an entangled initial state  of the two qubits at a point in flat Minkowski spacetime. Alice and Bob possess the first entry and the second entry in the ket, respectively. the unitary operator
of the two qubits at a point in flat Minkowski spacetime. Alice and Bob possess the first entry and the second entry in the ket, respectively. the unitary operator  is symmetric for fair games. The players perform their strategic moves as local unitary operators
is symmetric for fair games. The players perform their strategic moves as local unitary operators  belonging to a full space of SU(2) strategies, which is a set of three-parameter strategies:
belonging to a full space of SU(2) strategies, which is a set of three-parameter strategies:
 (1)
(1)

Table 1. Payoff matrix for the classical Battle of Sexes. The first entry in a pair of numbers denotes the payoff of Alice and the second entry stand for Bob’s payoff.

Table 2. The quantization scheme by the Eisert protocol: classical pure strategies B (Ballet) and F (Football) correspond to the quantum pure strategies  and
and , respectively.
, respectively.
where .
.
With classical strategic moves, .
.
The unitary operator  is an entangling operator and then is given by
is an entangling operator and then is given by
 (2)
(2)
where 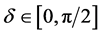 and is a measure of the degree of entanglement in the initial state. The initial state is maximally entangled for the upper limit of
and is a measure of the degree of entanglement in the initial state. The initial state is maximally entangled for the upper limit of  and has no entanglement for the lower limit of
and has no entanglement for the lower limit of .
.
The entangling operators 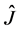 must be known to both players for the knowledge of the degree of the entanglement in the initial state. After the application of the entangling operator, the state of the game evolves to
must be known to both players for the knowledge of the degree of the entanglement in the initial state. After the application of the entangling operator, the state of the game evolves to
 (3)
(3)
We assume that Alice stays stationary and Bob moves with a uniform acceleration. Each player possesses a device which is sensitive only to a single mode in their respective regions. From the accelerated player Bob’s frame, the Minkowski vacuum state is given by a two-mode squeezed state,
 (4)
(4)
where . The parameter
. The parameter  is the dimensionless parameter, which
is the dimensionless parameter, which  when
when 
and 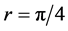 when
when . The constants
. The constants ,
,  , and
, and , in the above equation stand, respectively, for the Dirac particle's frequency, light speed in vacuum and Bob’s acceleration. In the Equation (4),the subscripts I and II of the kets represent the Rindler modes in the region I and II, respectively, in the Rindler spacetime diagram Figure 1. The Equation (4) represents that the noninertial observer that moves with a constant acceleration in region I observes a thermal state instead of the vacuum state, which is called Unruh effect [25] [26] .
, in the above equation stand, respectively, for the Dirac particle's frequency, light speed in vacuum and Bob’s acceleration. In the Equation (4),the subscripts I and II of the kets represent the Rindler modes in the region I and II, respectively, in the Rindler spacetime diagram Figure 1. The Equation (4) represents that the noninertial observer that moves with a constant acceleration in region I observes a thermal state instead of the vacuum state, which is called Unruh effect [25] [26] .
The excited state in Minkowski spacetime is relevant to Rindler modes as follows:
 (5)
(5)
In terms of Minkowski mode for Alice and Rindler modes for Bob, the entangled initial state of Equation (3) by exploiting Equations (4) and (5) evolves
 (6)
(6)
The corresponding mixed density matrix in the entangled initial state in Equation (6) is defined as
 (7)
(7)

Figure 1. Rindler spacetime diagram: The uniformly accelerated observer Bob (B) moves on a hyperbola with constant acceleration a in the region I and is causally disconnected from the region II which a fictitious observer anti-Bob  moves on.
moves on.
A uniformly accelerated observer (Bob) in Rindler region I is causally disconnected from the other region at the opposite side Figure 1, therefore, we must take trace over all the mode in region II. After the trace eperation, the density matrix is expressed as
 , (8)
, (8)
Note that the subscripts of the kets and bras have been dropped for simplicity. The density matrix can also be written as the following matrix:
 (9)
(9)
In the quantum Battle of the Sexes, each player has two possible strategies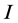 , the identity operator, and
, the identity operator, and , the inversion operator or the Pauli’s bit-flip operator. Let
, the inversion operator or the Pauli’s bit-flip operator. Let  and
and  represent the probabilities of
represent the probabilities of  and
and  that Alice applies. Similarly,
that Alice applies. Similarly,  and
and  are the probabilities that Bob applies the identity operator and inversion operator, respectively. After the players take their strategic moves, the final density matrix evolves to
are the probabilities that Bob applies the identity operator and inversion operator, respectively. After the players take their strategic moves, the final density matrix evolves to
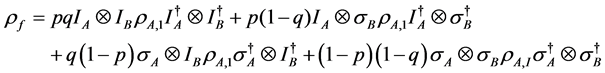 (10)
(10)
The payoff operators for Alice and Bob can be written as
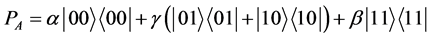 (11)
(11)
 (12)
(12)
The payoff functions for Alice and Bob in the Battle of the Sexes respectively, are
 (13)
(13)
For the sake of convenience, the following variables can be defined:
 (14)
(14)
 (15)
(15)
 (16)
(16)
 (17)
(17)
By using the above variables, the payoff functions in Equation (13) can be expressed in the following succinct way:
 (18)
(18)
The payoff functions in Equation (18) show the expected gains of both players depend on not only the probability distributions  and
and  for Alice and Bob respectively, but also on the degree of entanglement
for Alice and Bob respectively, but also on the degree of entanglement  and dimensionless acceleration parameter
and dimensionless acceleration parameter . Furthermore, even in the case of unentangled initial state (i.e.
. Furthermore, even in the case of unentangled initial state (i.e. ), the expected payoff functions depend on the probability distributions of both players and as well vary with the the acceleration
), the expected payoff functions depend on the probability distributions of both players and as well vary with the the acceleration  of Bob.
of Bob.
Before we continue, let us first find some relationships about the variables defined in Equations (14)-(17):
 (19)
(19)
The value of  is not always positive. It could be nonnegative for some domains of
is not always positive. It could be nonnegative for some domains of  and
and  since
since
 is true for the fact that
is true for the fact that . For instance
. For instance  when
when  and
and
 .
.
For the same sake, we can obtain the following inequalities:
 (20)
(20)
 (21)
(21)
 (22)
(22)
For the definite degree of entanglement  and the acceleration of Bob, the expected payoff functions can be rewritten as follows:
and the acceleration of Bob, the expected payoff functions can be rewritten as follows:
 (23)
(23)
Nash Equilibria can be found by imposing the two coupled inequalities:
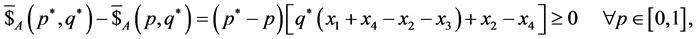 (24)
(24)
 (25)
(25)
3. Results and Analysis
When two factors in both inequalities are both the same sign, we can get the Nash Equilibrium. There are three possibilities:
Case 1. ,
, . In such a case both Alice and Bob play the pure strategy B (Ballet). their expected payoff functions are
. In such a case both Alice and Bob play the pure strategy B (Ballet). their expected payoff functions are  and
and , and by employing the in equalities (20) and (22) the following inequalities hold:
, and by employing the in equalities (20) and (22) the following inequalities hold:
 (26)
(26)
 (27)
(27)
The payoff functions in Nash Equilibriua are relevant to the degree of entanglement of the initial state and the dimensionless acceleration parameter . In inertial frame, the parameter
. In inertial frame, the parameter , the payoffs of both players coincide when the initial state is in maximally entangled. In this particular situation, the gains of both players are
, the payoffs of both players coincide when the initial state is in maximally entangled. In this particular situation, the gains of both players are
 respectively. In the noninertial frame, the payoff function, taking the gain of Alice for instance, is strongly influenced by the acceleration parameter
respectively. In the noninertial frame, the payoff function, taking the gain of Alice for instance, is strongly influenced by the acceleration parameter  such that the gain of Alice is given by
such that the gain of Alice is given by , which becomes
, which becomes
 when player Bob is assumed to move in an infinite acceleration corresponding to the parameter
when player Bob is assumed to move in an infinite acceleration corresponding to the parameter .
.
Case 2. ,
, . In this case both Alice and Bob play the another pure strategy F (Football). Their expected payoff functions are reversed with respect to the previous case:
. In this case both Alice and Bob play the another pure strategy F (Football). Their expected payoff functions are reversed with respect to the previous case:  and
and .
.
Meanwhile, by the equation (19) we get following truth:
The payoff function of Alice
 (28)
(28)
is not always nonnegative for the nonpositive-definite value of . In such a case this pure strategy is not the Nash Equilibrium when the value of
. In such a case this pure strategy is not the Nash Equilibrium when the value of  is negative. The new Nash equilibria could arise when
is negative. The new Nash equilibria could arise when  is positive by choosing the degree of entanglement in the initial state and the acceleration of Bob.
is positive by choosing the degree of entanglement in the initial state and the acceleration of Bob.
By inequality (21) we get the following inequality for the payoff function of Bob:
 (29)
(29)
In the inertial frame , the payoff functions are
, the payoff functions are  and
and
 , respectively. If two players share an unentangled initial state
, respectively. If two players share an unentangled initial state , the gains of the players in noninertial frame are
, the gains of the players in noninertial frame are  and
and , which are relevant to the dimensionless acceleration parameter
, which are relevant to the dimensionless acceleration parameter .
.
Case 3. When the probabilities  and
and  are less than one but greater than zero, two of the factors in inequalities (24) and (25) should be reasonable to be zero. Hence, we can solve the probabilities:
are less than one but greater than zero, two of the factors in inequalities (24) and (25) should be reasonable to be zero. Hence, we can solve the probabilities:
 and
and 
which correspond to the gains of both Alice and Bob coincide:
 (30)
(30)
The new Nash Equilibria are relevant to acceleration of Bob and degree of entanglement in the initial state for the value of . When the value of
. When the value of 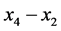 is negative, the probability distribution of Bob is meaningless and it is so far from the purpose that we could get new Nash Equilibrium.
is negative, the probability distribution of Bob is meaningless and it is so far from the purpose that we could get new Nash Equilibrium.
In the case of unentangled initial state (i.e. ), the equations (14)-(17) are reduced into the following equations:
), the equations (14)-(17) are reduced into the following equations:
 (31)
(31)
By using these equations, we can receive that  and
and
 , by which the gains of players are obtained:
, by which the gains of players are obtained:
 .
.
4. Discussions and Conclusions
As we can find from Eqautions (14)-(17) that ,
,  ,
,  , and
, and  when the initial state is unentangled and both Alice and Bob are in the inertial frame (i.e.
when the initial state is unentangled and both Alice and Bob are in the inertial frame (i.e. ). In such case, the payoff functions for players correspond to the classical game and their expected payoffs are:
). In such case, the payoff functions for players correspond to the classical game and their expected payoffs are:
 (32)
(32)
In this classical mixed strategies, three Nash Equilibria can be found [22] : 1) probability distribution ( ,
, ) corresponds to pure strategy that both Alice and Bob choose to play B. Their expected payoff functions are
) corresponds to pure strategy that both Alice and Bob choose to play B. Their expected payoff functions are  and
and . 2) Strategies
. 2) Strategies  and
and  correspond to pure strategy, both Alice and Bob play F, and expected payoffs are
correspond to pure strategy, both Alice and Bob play F, and expected payoffs are  and
and . 3)
. 3)  and
and
 , which are correctly larger than zero and less than one, correspond to a Nash Equilibrium for which the payoffs of both players coincide:
, which are correctly larger than zero and less than one, correspond to a Nash Equilibrium for which the payoffs of both players coincide: .
.
In a summary, we have shown that payoff functions are strongly influenced by the acceleration of moving player Bob in the noninertial frame. Payoff functions are affected by Unruh effect in the quantum Battle of the Sexes in noninertial frame. In the case of Battle of Sexes, the Nash Equilibria in inertial frame are still equilibria in the corresponding noninertial frame but the payoffs of both Alice and Bob are relevant to both degree of entanglement in the players’ initial state and the acceleration parameter. In the case of probability distribution
 , it is a new Nash Equilibrium for the probability distributions of both play are related to the degree of entanglement and acceleration parameter, which can be backward induced to the inertial situation when we suppose the dimensionless accelerating parameter
, it is a new Nash Equilibrium for the probability distributions of both play are related to the degree of entanglement and acceleration parameter, which can be backward induced to the inertial situation when we suppose the dimensionless accelerating parameter . In the limit of infinite acceleration, we find that the payoff functions at the Nash Equilibria would be irrelevant to the acceleration but only depend on the entanglement.
. In the limit of infinite acceleration, we find that the payoff functions at the Nash Equilibria would be irrelevant to the acceleration but only depend on the entanglement.
Acknowledgements
This work is supported by the National Key Projects for Basic Researches of China (No. 2011CB922104, 2011CBA00200), by the National Natural Science Foundation of China (No. 91021003, 11274156), the Natural Science Foundation of Jiangsu Province(No. BK2010012), and PAPD.