An Improved Analytical Model for IEEE 802.11 Distributed Coordination Function under Finite Load ()
1. Introduction
IEEE 802.11 has been standardized and widely adopted for wireless local area networks (WLANs) [1]. In this standard, it specifies two fundamental access mechanisms, i.e., point coordination function (PCF) and distributed coordination function (DCF). Since IEEE 802.11 DCF mechanism supports adhoc networking configuration and has been widely adopted in wireless networks, we focus our analysis only on this mechanism. DCF mechanism is based on the carrier sense multiple access with collision avoidance (CSMA/CA) protocol. In DCF, data frames are transmitted via two mechanisms, i.e., basic access mechanism and request-to-send/clear-tosend (RTS/CTS) mechanism.
Performance analysis of DCF has been reported in several research works through either simulation or mathematical modeling [2-13]. The Markov model proposed in [2] for IEEE 802.11 DCF has gained wide acceptance due to its simplicity. However, it exhibits some constraints according to [1]. First, the model is limited to deriving the saturation throughput. It excludes the performance analysis under finite load condition, which is an important practical scenario in a WLAN. Secondly, it does not take into account the loss of frames due to channel contention. This frame loss has been shown to be significant in [10]. Finally, decrementing a backoff value by a station (STA) is not modeled correctly as per 802.11 standard [1].
In the literature, some investigations have been reported on finite load models for IEEE 802.11 DCF, [3,4,11-14]. In [4], the authors extend the model reported in [2], for finite load by introducing a new state accounting for the case in which STA’s queue is empty after successful transmission of a packet. Throughput has been expressed as a function of queue utilization under the perfect channel assumption. In [3], a queuing model has been proposed to study delay and queue length characteristics at each STA under finite load conditions. In [11,12], authors propose a Markov model for characterizing the IEEE 802.11 DCF behavior by including transmission states that account for packet transmission failures due to errors caused by propagation through channel. Also, a state has been introduced characterizing the situation when an STA has no packets to transmit. In [13], authors proposed a Markov model for limited load by adding a new state for each backoff stage accounting for the absence of new packets to be transmitted. In [14], a Markov model is proposed to analyze the IEEE 802.11 DCF under finite load. Performance has been analyzed in terms of channel throughput and average packet delay under perfect and a slow Rayleigh fading channel. However, in all the proposed models, decrementing a backoff value by an STA is not correctly modeled according to [1]. As per the standard [1], an STA in any backoff stage should decrement its backoff counter value only when the channel status is found to be idle for at least DCF inter-frame space (DIFS) duration. Whereas in the proposed models, an STA decrements its backoff counter value irrespective of the channel status i.e., whether the channel is busy or idle, which is not complying with [1]. In this work, we follow the models in [2,14]. Hereafter, we refer to model in [2] as Bianchi's model and model in [14] as Pham's model. Readers are requested to refer [1] for a detailed discussion on IEEE 802.11 DCF operation.
In this paper, we propose an improved Markov model for IEEE 802.11 DCF under finite load by closely following the specifications in [1]. The model is investigated in terms of channel throughput under perfect and slow Rayleigh fading channels for different packet arrival rate and number of STAs in the network.
The rest of the paper is organized as follows: Section 2 describes the proposed Markov model for IEEE 802.11 DCF under finite load, followed by the performance analysis for perfect channel conditions. The model developed in Section 2 is extended for a slow Rayleigh fading channel and the performance is analyzed in Section 3. Finally Section 4 presents the concluding remarks on the work.
2. Markov Model for IEEE 802.11 DCF
As discussed above, the Markov models presented in literature have shortcomings. Complementing the work in [2,14], we focus on the performance analysis of IEEE 802.11 DCF under finite load condition. The saturation throughput considered in [2] is just one particular case of our analysis. We divide our contribution into two parts. In the first part, we propose an improved Markov model for DCF assuming perfect channel conditions. Next, we extend this model for a slow Rayleigh fading channel. For simplicity, we use the same notation as given in [14].
2.1. Proposed Markov Model for IEEE 802.11 DCF
Let 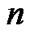 be the number of stations (STAs) in a WLAN contending for channel access. Let
be the number of stations (STAs) in a WLAN contending for channel access. Let  and
and 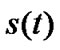 be the stochastic processes representing the backoff counter and number of the backoff stages respectively. The backoff states and its transition probabilities for a given STA are shown in Figure 1. The parameters used in our model are described in Table 1. We assume that the channel is perfect (i.e., error free) and the packets are lost only due to collisions.
be the stochastic processes representing the backoff counter and number of the backoff stages respectively. The backoff states and its transition probabilities for a given STA are shown in Figure 1. The parameters used in our model are described in Table 1. We assume that the channel is perfect (i.e., error free) and the packets are lost only due to collisions.
Under saturation condition, an STA always has a packet for transmission in its queue. Therefore, it enters straight away to state S0,k,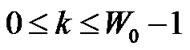 . However, under finite load, if the STA’s queue is empty, the station enters into one of the states
. However, under finite load, if the STA’s queue is empty, the station enters into one of the states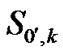 ,
,  , otherwise the STA enters one of the backoff states S0,k,
, otherwise the STA enters one of the backoff states S0,k, . At state S0',0, if there is a packet for transmission, the STA starts transmitting the packet by moving to the state S0,0 with probability P0',0. Otherwise, the STA enters the state Sidle,0 with probability P0',idle. At state Sidle,0 once a frame arrives into the queue of a STA and if the channel has been found to be idle for more than DIFS, this frame is transmitted immediately with probability Pidle,0. Otherwise, the STA goes to backoff state S0,k,
. At state S0',0, if there is a packet for transmission, the STA starts transmitting the packet by moving to the state S0,0 with probability P0',0. Otherwise, the STA enters the state Sidle,0 with probability P0',idle. At state Sidle,0 once a frame arrives into the queue of a STA and if the channel has been found to be idle for more than DIFS, this frame is transmitted immediately with probability Pidle,0. Otherwise, the STA goes to backoff state S0,k, 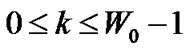 with probability Pidle,b.
with probability Pidle,b.
The state of each STA is described by , where
, where  indicates the current backoff stage,
indicates the current backoff stage, 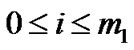 and k is the backoff counter value measured in time slots,
and k is the backoff counter value measured in time slots, .
.

Figure 1. Two dimensional Markov chain for IEEE 802.11 DCF backoff mechanism.
The Markov chain in Figure 1 is described in the following:
1) The backoff counter value is decremented when the STA senses the channel is idle for at least DIFS duration:

where  =
= is the probability that the channel is found to be busy when at least one of the STAs transmits at a given slot time.
is the probability that the channel is found to be busy when at least one of the STAs transmits at a given slot time.
2) The backoff counter value is frozen whenever the STA senses that the channel is busy:

The above steps (1) and (2) are not included in the existing Markov models.
3) When at least one new frame has arrived at STA’s queue during mandatory backoff stage (i.e.,  ,
, ) then
) then .
.
4) If no frames have arrived during mandatory backoff stage and the STA enters into the IDLE state:

5) If at least one frame has arrived when an STA is in the IDLE state and the station senses the channel is idle for at least DIFS duration: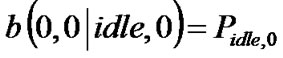 .
.
6) When at least one frame has arrived and the STA senses the channel is busy:

7) The frame is not transmitted successfully by an STA in a backoff stage:

8) The frame has been transmitted successfully and there is at least one more packet in the queue of an STA:

9) The frame is transmitted successfully or lost in collision at  backoff stage and there is no packet in the queue:
backoff stage and there is no packet in the queue:
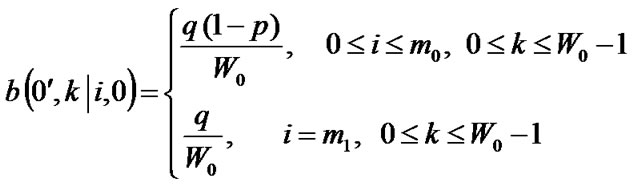
Next, we derive the closed-form solution for the proposed Markov model. In the steady-state, let 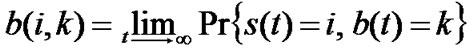 be the stationary distribution of the Markov chain. All steady-state probabilities are expressed as a function of
be the stationary distribution of the Markov chain. All steady-state probabilities are expressed as a function of 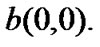
We observe that,
 (1)
(1)
Or

From (1), it is easy to derive the following,
 (2)
(2)
And also, we can find that,
 (3)
(3)
For , we can derive the following,
, we can derive the following,
 (4)
(4)
when i = k =0, we obtain,
 (5)
(5)
For , we get,
, we get,
 (6)
(6)
And also, for ,
,
 (7)
(7)
Substituting (2) and (3) in (7), we obtain,
 (8)
(8)
And also, we can show that,
 (9)
(9)
We observe that,
 (10)
(10)
Substituting (9) in (10) and using the relation  yields,
yields,
 (11)
(11)
Under steady state,  is determined by imposing the normalizing condition,
is determined by imposing the normalizing condition,
 (12)
(12)
where 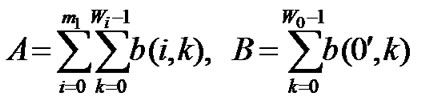 and
and 
 (13)
(13)
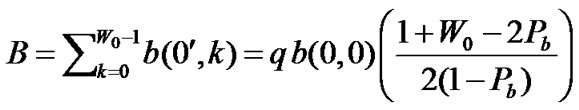 (14)
(14)
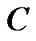 can be expressed as:
can be expressed as:
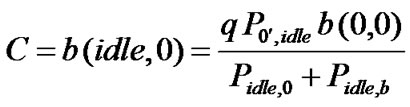 (15)
(15)
Substituting (13), (14) and (15) in (12), we obtain,
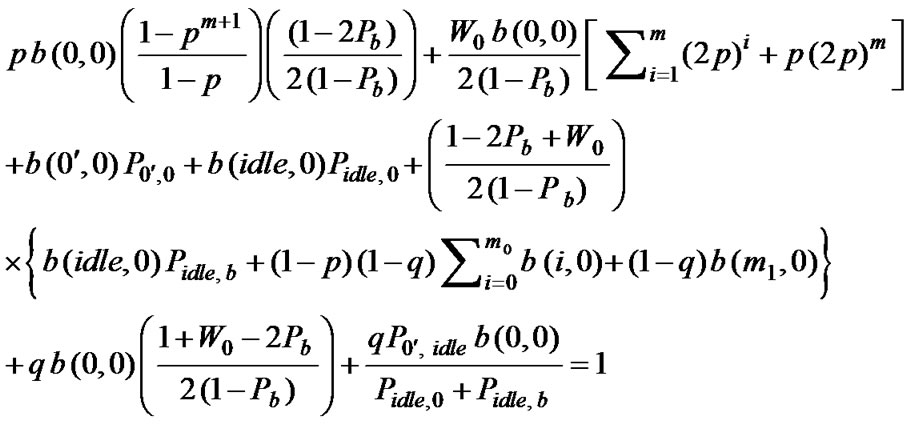 (16)
(16)
Therefore,  can be obtained as,
can be obtained as,
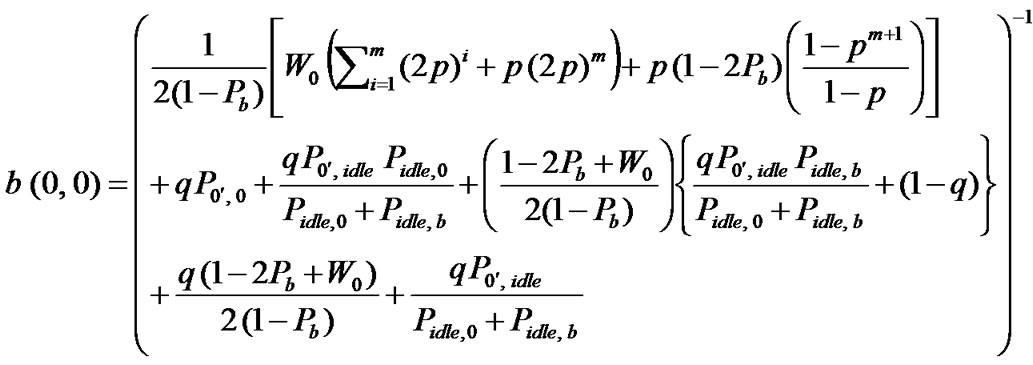 (17)
(17)
After rearranging some terms, we can write 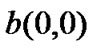 as,
as,
 (18)
(18)
It is important to note that, if we substitute Pb = 0 in (18), proposed model reduces to Pham’s model in [14]. Further, by letting q = 0 (i.e., STA’s queue is never empty) and introducing the constraint that packet will never be dropped even after reaching maximum retry limit, Equation (18) reduces to the same expression as in [2]. This confirms the fact that we have covered Bianchi’s model also.
Using 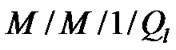 queuing model in [15], the probability that the queue of any STA is empty is,
queuing model in [15], the probability that the queue of any STA is empty is,
 (19)
(19)
where λ is the average packet arrival rate and 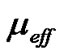 is the effective packet service rate.
is the effective packet service rate.
The probabilities 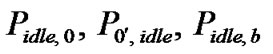 and
and 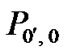 are same as in [14]. IEEE 802.11 packet format consists of an actual payload (
are same as in [14]. IEEE 802.11 packet format consists of an actual payload ( ) and header information (
) and header information ( ). We know that the channel can be in any of the three states in a slot, i.e., idle (
). We know that the channel can be in any of the three states in a slot, i.e., idle ( ) or busy due to successful transmission (
) or busy due to successful transmission ( ) or busy due to packet collisions (
) or busy due to packet collisions ( ).
).
Using the basic access mechanism of IEEE 802.11 DCF,  and
and  can be calculated as:
can be calculated as:
 (20)
(20)
where SIFS, ACK, DIFS and δ are the short inter-frame space, acknowledgement, DCF inter-frame space and channel propagation delay respectively.
Because each STA transmits with probability , we have the following expressions:
, we have the following expressions:
 (21)
(21)
Each time slot has the probability ( ) of being idle,
) of being idle,  of having a successful transmission and
of having a successful transmission and 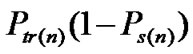 of having a packet collision. Therefore, the average slot time can be calculated as:
of having a packet collision. Therefore, the average slot time can be calculated as:
 (22)
(22)
The states  and
and ,
, 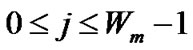 , represent the last two backoff stages as shown in Figure 1. According to [1], the sending STA attempts to send the DATA packet under basic access scheme for station short retry count times before discarding the packet. Therefore,
, represent the last two backoff stages as shown in Figure 1. According to [1], the sending STA attempts to send the DATA packet under basic access scheme for station short retry count times before discarding the packet. Therefore, 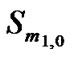 is the state where a given packet is either transmitted successfully with probability
is the state where a given packet is either transmitted successfully with probability  or permanently discarded with probability p. Furthermore, denoting m0 and m1 as the indices of the last two backoff stages, we have,
or permanently discarded with probability p. Furthermore, denoting m0 and m1 as the indices of the last two backoff stages, we have,
 (23)
(23)
The probability for a given STA to transmit can be easily derived by noticing that the STA can only transmit after its backoff timer expires, that is,
 (24)
(24)
The transmitted packet is not received correctly by the receiver when at least two STAs transmit at the same time. In other words, this is equal to the probability of at least one out of  remaining STAs transmits, that is,
remaining STAs transmits, that is,
 (25)
(25)
We can rewrite (25) and obtain transmission probability as,
 (26)
(26)
Using (24) and (26), p and  are readily obtained using numerical analysis.
are readily obtained using numerical analysis.
2.2. Channel Throughput
In this section, we derive the expression for channel throughput which is the performance metric to evaluate our proposed model. For a finite load where the packet arrival rate ( ) is less than effective packet service rate (
) is less than effective packet service rate ( ), the STA’s throughput (
), the STA’s throughput ( ) is the portion of traffic that arrived minus the portion that is discarded, i.e.,
) is the portion of traffic that arrived minus the portion that is discarded, i.e., 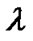 (
( ), where Pdisc is the probability that the packet is discarded. Here, we assume an M/M/1/Ql model for transmission queue, hence packet arrival rate (
), where Pdisc is the probability that the packet is discarded. Here, we assume an M/M/1/Ql model for transmission queue, hence packet arrival rate ( ), throughput at an STA (
), throughput at an STA ( ), and the total normalized throughput for a neighborhood of n identical STAs (
), and the total normalized throughput for a neighborhood of n identical STAs ( ), are given by (27). Further,
), are given by (27). Further,  , where
, where  indicates the rate of successful transmissions and
indicates the rate of successful transmissions and  indicates the rate at which packets are being discarded. Therefore, traffic intensity (ρ)=
indicates the rate at which packets are being discarded. Therefore, traffic intensity (ρ)= and,
and,

 (27)
(27)
For a large queue length (Ql) and ,
,  is taken equivalent to
is taken equivalent to  since
since  is negligible. Under saturation condition (i.e.,
is negligible. Under saturation condition (i.e.,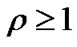 ), maximum successful packet transmission rate (
), maximum successful packet transmission rate (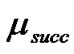 ) is given by,
) is given by,
 (28)
(28)
where  is the average slot duration and
is the average slot duration and 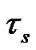 is the probability of packet transmission by an STA at saturation.
is the probability of packet transmission by an STA at saturation.
2.3. Performance Analysis of the Proposed Model
In this section, we present the results and discuss the variation of channel throughput with different packet arrival rate and different number of STAs in a network under perfect channel assumption. The parameters used in the evaluation of our proposed analytical model are same as in [14] and are reproduced in Table 2 for ready

Figure 2. Channel throughput vs. packet arrival rate with varying number of STAs.
reference. In our analysis, we have considered basic access mechanism of DCF. However, it is easy to extend our analysis for RTS/CTS-based access mechanism of DCF as well.
In order to verify our proposed analytical model, we compare theoretical analysis discussed earlier to the simulation results in Figure 2. This figure illustrates that the simulation results agree well with analytical results.
In Figure 3 we observe the impact of packet arrival rate on channel throughput as number of STAs varies. It is clear that for a given number of STAs in the network, increase in the packet arrival rate increases the channel throughput linearly in both models as long as the packet arrival rate is less than packet processing rate. However, as the channel throughput reaches its maximum, further increase in packet arrival rate makes channel throughput to saturate. This is because all STAs have a packet to transmit at any given slot. That is, packet arrival rate is more than the packet processing rate, which causes the saturation of throughput. It is observed that proposed model shows increase in throughput with an improvement of 1 to 4% compared to Pham’s model [14] with increase in number of STAs (n) from 4 to 30. This improvement is due to the checking of channel status in our proposed model before decrementing the backoff counter value according to [1], which in turn decreases the probability of collisions and hence increases the probability of successful transmissions. This is also confirmed in Figure 5. However, at low packet arrival rate, performance of the proposed model is similar to Pham’s model. This is

Table 2. Summary of IEEE 802.11 DCF parameters.
because the number of competing STAs is small and also the packet arrival rate is less, and hence channel status may be idle for most of the time. We also find that maximum throughput value gets shifted to a lower value with increase in number of STAs. This is obvious as the number of competing STAs increases, probability of packet collisions increases consequently.
Figure 4 shows the variation of channel throughput with number of STAs for a given packet arrival rate. We observe that increasing the number of STAs increases the channel throughput linearly till a maximum value is reached in both the models. However, further increase in number of STAs after the throughput reaches a maximum value; we observe that the throughput decreases. This is because of the fact that increase in number of STAs increases packet collisions and hence reduction in throughput. It is observed that the proposed model shows increase in throughput with an improvement of 2 to 4% compared to Pham’s model with increase in number of STAs (n) from 8 to 50 for a fixed packet arrival rate of 15 packets/sec. This im-