1. Introduction
The Gronwall type integral inequalities provide a necessary tool for the study of the theory of differential equations, integral equations and inequalities of the various types (please, see Gronwall [1] and Guiliano [2] ). Some applications of this result to the study of stability of the solution of linear and nonlinear differential equations may be found in Bellman [3] . Numerous applications to the existence and uniqueness theory of differential equations may be found in Nemyckii-Stepanov [4] , Bihari [5] , and Langenhop [6] . During the past few years several authors (see references below and some of the references cited therein) have established several Gronwall type integral inequalities in one or two independent real variables [1] -[14] . Of course, such results have application in the theory of partial differential equations and Volterra integral equations.
In [14] , Pachpatte investigated the following inequality:
Lemma: Let  be nonnegative continuous functions defined on
be nonnegative continuous functions defined on  and
and 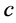 be nonnegative constant. Let
be nonnegative constant. Let  be a nonnegative continuous function defined for
be a nonnegative continuous function defined for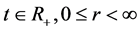 , and monotonic nondecreasing with respect to
, and monotonic nondecreasing with respect to  for ant fixed
for ant fixed . If
. If

For , then
, then

where  is the maximal solution of
is the maximal solution of

For .
.
2. Main Results
Theorem 2.1: Let  and
and  be nonnegative continuous functions defined on
be nonnegative continuous functions defined on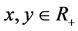 . Let
. Let  be a positive continuous and nondecreasing functions in both variables and defined for
be a positive continuous and nondecreasing functions in both variables and defined for . If
. If
 (2.1)
(2.1)
Then

where 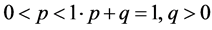 and
and
 , (2.2)
, (2.2)
and  is the maximal solution of
is the maximal solution of
 (2.3)
(2.3)
Proof: Define a function 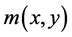 by the right-hand side of (2.1).Then
by the right-hand side of (2.1).Then
 (2.4)
(2.4)
By using (2.4) in (2.1), we get
 (2.5)
(2.5)
Since  is a positive continuous and nondecreasing function, then
is a positive continuous and nondecreasing function, then
 (2.6)
(2.6)
Let
 (2.7)
(2.7)
From (2.6) and (2.7), we observe that
 (2.8)
(2.8)
And
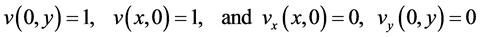 (2.9)
(2.9)
Differentiating both sides of (2.8) with respect to 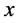 and
and , we get
, we get

 (2.10)
(2.10)
By keeping first  fixed in (2.10) and set
fixed in (2.10) and set  and integrate from 0 to
and integrate from 0 to  then again keeping
then again keeping 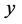 fixed, set
fixed, set  and integrate from 0 to
and integrate from 0 to  respectively and using (2.9), we get
respectively and using (2.9), we get
 (2.11)
(2.11)
From (2.7) and (2.11), it is clear that

From (2.4), it can be restated as

where  is the maximal solution of
is the maximal solution of

This completes the proof.
Theorem 2.2: Let  be defined as in Theorem 2.1. If
be defined as in Theorem 2.1. If
 (2.12)
(2.12)
Then

where  and
and
 , (2.13)
, (2.13)
where  is the maximal solution of
is the maximal solution of

Proof: Define a function  by the right-hand side of (2.12).Then
by the right-hand side of (2.12).Then
 (2.14)
(2.14)
By using (2.14) in (2.12), we get
 (2.15)
(2.15)
By following the same steps of Theorem 2.1 from (2.5)-(2.11), we get
 (2.16)
(2.16)
From (2.7), (2.14) and (2.16), we observe that

where 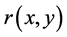 is the maximal solution of
is the maximal solution of

This completes the proof.
Theorem 2.3: Let  be defined as in Theorem 2.1. If
be defined as in Theorem 2.1. If
 (2.17)
(2.17)
Then

where  and
and
 , (2.18)
, (2.18)
where  is the maximal solution of
is the maximal solution of

Proof: Define a function  by the right-hand side of (2.17).Then
by the right-hand side of (2.17).Then
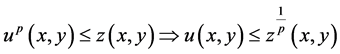 (2.19)
(2.19)
where 
By using (2.19) in the above equation, we get
 (2.20)
(2.20)
and
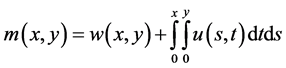 (2.21)
(2.21)
Since 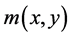 is a positive continuous and nondecreasing function, then from (2.20),
is a positive continuous and nondecreasing function, then from (2.20),
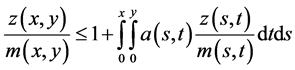 (2.22)
(2.22)
Let
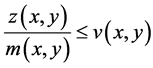 (2.23)
(2.23)
where
 (2.24)
(2.24)
And
 (2.25)
(2.25)
Differentiating both sides of (2.24) with respect to 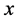 and
and , and from (2.23), we get
, and from (2.23), we get

 (2.26)
(2.26)
By keeping first x fixed in (2.26) and set  and integrate from 0 to y then again keeping y fixed, set
and integrate from 0 to y then again keeping y fixed, set  and integrate from 0 to x respectively and using (2.25), we get
and integrate from 0 to x respectively and using (2.25), we get
 (2.27)
(2.27)
From (2.19), (2.23) and (2.27), it is clear that

where  is the maximal solution of
is the maximal solution of

This completes the proof.
Application: As an application, let us consider the bound on the solution of a nonlinear hyperbolic partial differential equation of the form
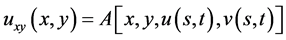 (2.28)
(2.28)
with the given boundary conditions
 (2.29)
(2.29)
where  and
and  such that
such that
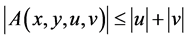 (2.30)
(2.30)
 (2.31)
(2.31)
where 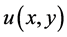 and
and  be nonnegative continuous functions defined on a domain D
be nonnegative continuous functions defined on a domain D
 . The Equation (2.28) with (2.29) is equivalent to the integral equation
. The Equation (2.28) with (2.29) is equivalent to the integral equation
 (2.32)
(2.32)
Let  be any solution of (2.28) with (2.29) and taking absolute values of both sides, we get
be any solution of (2.28) with (2.29) and taking absolute values of both sides, we get
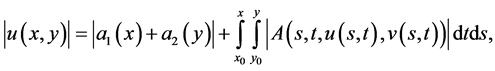 (2.33)
(2.33)
Using (2.30)-(2.32) in (2.33) and assuming that , where
, where 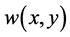 be a positive continuous and nondecreasing function defined in the respective domain, we have
be a positive continuous and nondecreasing function defined in the respective domain, we have

Then 
where , and
, and  is the maximal solution of
is the maximal solution of
 The remaining proof will be the same as the proof of Theorem 2.1 with suitable modifications.
The remaining proof will be the same as the proof of Theorem 2.1 with suitable modifications.
We note that Theorem 2.1 can be used to study the stability, boundedness and continuous dependence of the solutions of (2.28).