An Iterative Method for Solving Two Special Cases of Lane-Emden Type Equation ()
1. Introduction
Other classical nonlinear equation, which has been the object of much study, is Lane-Emden’s equation. This equation has the form
 (1)
(1)
with  and the subject to initial conditions
and the subject to initial conditions
 (2)
(2)
where  and
and  are constants and
are constants and  is a real-valued continuous function where
is a real-valued continuous function where  and
and 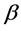 are constants and
are constants and  is a real-valued continuous function. The Equation (1) was used to model various problems, including the isothermal gas spheres, theory of thermionic currents and the gravitational potential of stars [1] among others.
is a real-valued continuous function. The Equation (1) was used to model various problems, including the isothermal gas spheres, theory of thermionic currents and the gravitational potential of stars [1] among others.
Let us consider a spherical cloud of gas (see Figure 1) and denote its hydrostatic pressure at a distance  from the centre by
from the centre by . Let
. Let  be the mass of the spheres of radius
be the mass of the spheres of radius  the gravitational potential of the gas and
the gravitational potential of the gas and  the acceleration of gravity.
the acceleration of gravity.
Then, we have the following equation
 (3)
(3)
where  is the gravitational constant.
is the gravitational constant.
Thus, three conditions are assumed for the determination of 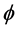 and
and 
 (4)
(4)
where 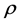 is the density of the gas.
is the density of the gas.
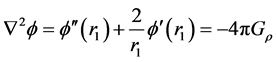 (5)
(5)
and
 (6)
(6)
where  and
and  are arbitrary constants.
are arbitrary constants.
Now, solving (4) and (6) with  when
when  we have
we have
 (7)
(7)
or
 (8)
(8)
where  and
and . If this value of
. If this value of 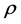 is replaced into Equation (5), we obtain
is replaced into Equation (5), we obtain
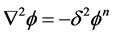 (9)
(9)
where .
.
Now, since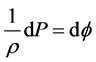 , by integration
, by integration , that is,
, that is, . If
. If  is the central densitythen
is the central densitythen  must be zero, a change from the condition in the previous case where
must be zero, a change from the condition in the previous case where 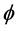 was zero only at the boundary of the sphere.
was zero only at the boundary of the sphere.
Poisson’s equation is now replaced by
 (10)
(10)
where , equation which is known as Liouville’s equation. If we assume symmetry as before, Equation (1) in polar coordinates reduces to the following
, equation which is known as Liouville’s equation. If we assume symmetry as before, Equation (1) in polar coordinates reduces to the following
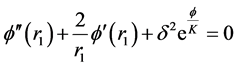 (11)
(11)
which replaces Equation (9).
If we let  and
and , then (11) becomes
, then (11) becomes
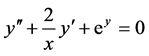 (12)
(12)
which is to solved subject to the boundary conditions  and
and . The counterpart [2] of the Equation (12) in which
. The counterpart [2] of the Equation (12) in which  is replaced by
is replaced by  appears in Richardson’s theory of thermionic currents when one seeks to determine the density and electric force of an electron gas in the neighborhood of a hot body in thermal equilibrium.
appears in Richardson’s theory of thermionic currents when one seeks to determine the density and electric force of an electron gas in the neighborhood of a hot body in thermal equilibrium.
Finally, now consider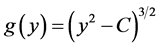 , then Equation (1) is turned to the white-dwarf equation, which introduced by [2] in his study of gravitational potential of the degenerate stars. This Equation is defined in the form
, then Equation (1) is turned to the white-dwarf equation, which introduced by [2] in his study of gravitational potential of the degenerate stars. This Equation is defined in the form

With 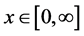 and subject to initial conditions
and subject to initial conditions  and
and . For instance if
. For instance if , we have Lane-Emden equation of index
, we have Lane-Emden equation of index  [3] .
[3] .
The Differential Transformation Method is a semi-numerical-analytic method for solving ordinary and partial differential equations. Zhou first introduced the concept of DTM in 1986 [4] . This technique constructs an analytical solution in the form of a polynomial. DTM is an alternative procedure for obtaining analytical Taylor series solution of the differential equations. The series often coincides with the Taylor expansion of the true solution at point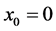 , in the value case, although the series can be rapidly convergent in a very small region.
, in the value case, although the series can be rapidly convergent in a very small region.
Many numerical methods were developed for this type of nonlinear ordinary differential equations, specifically on Lane-Emden type equations such as the Adomian Decomposition Method (ADM) [5] , the Homotopy Perturbation Method (HPM) [6] [7] , the Homotopy Analysis Method (HAM) [8] and Berstein Operational Matrix of Integration [9] . In this paper, we show superiority of DTM by applying them on the some type LaneEmden type equations. The power series solution of the reduced equation transforms into an approximate implicit solution of the original equation. A spectral method (Legendre-Spectral method) was proposed to solve white-dwarf equation; this spectral method provides the most convenient computer implementation [10] .
2. Description of DTM
Differential transformation method of the function 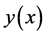 is defined as follows
is defined as follows
 (13)
(13)
In (13),  is the original function and
is the original function and  is the transformed function and the inverse differential transformation is defined by
is the transformed function and the inverse differential transformation is defined by
 (14)
(14)
In real applications, function 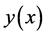 is expressed by a finite series and Equation (14) can be written as
is expressed by a finite series and Equation (14) can be written as
 (15)
(15)
Equation (15) implies that

The following theorems can be deduced from Equations (13) and (15).
Theorem 1 .
.
Theorem 2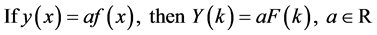 .
.
Theorem 3 .
.
Theorem 4 .
.
Theorem 5 
Theorem 6 (Cárdenas) 
The proofs of Theorems are available in [11] .
3. Test Problems
To illustrate the ability of DTM for the Lane-Emden type equation, three examples are provided. The results reveal that this method is very effective.
Example 1 Consider the nonlinear initial-value problem  subject to
subject to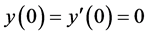 . Multiplying both sides by
. Multiplying both sides by  we obtain
we obtain
 (16)
(16)
Applying theorems 1-6 to Equation (16)
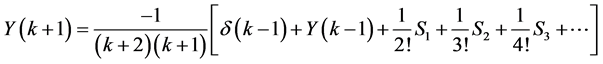 (17)
(17)
where
 (18)
(18)
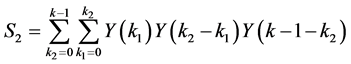 (19)
(19)
 (20)
(20)
for all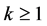 .
.
Now, from the initial conditions  we can obtain
we can obtain
 (21)
(21)
Substituting Equation (21) into Equation (17) and by recursive method, the results are listed as follows.
 .
.

and then, . For
. For  we have:
we have:
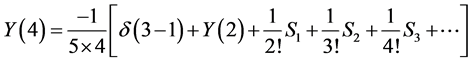
Now, as  and
and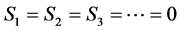 , then
, then 
For  we have:
we have:

In this case as  and
and , then
, then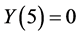 .
.
The lector can see that

For  we have:
we have:

Now, we can see:

 and then
and then

For 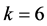 we have:
we have:

Here,

and

and so, . Consequently,
. Consequently, .
.
For 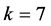 we have:
we have:

Here

and

Consequently, . Finally,
. Finally,

Therefore using (15), the closed form of the solution can be easily written as:

A series solution obtained by Wazwaz [5] and series expansion respectively is
 (22)
(22)
Table 1 shows the comparison of  obtained by the DTM (method proposed in this work) and those obtained by Wazwaz. The resulting graph of the isothermal gas spheres equation in comparison to the present method and those obtained by Wazwaz is shown in Figure 2.
obtained by the DTM (method proposed in this work) and those obtained by Wazwaz. The resulting graph of the isothermal gas spheres equation in comparison to the present method and those obtained by Wazwaz is shown in Figure 2.
Example 2 Consider the following problem  subject to
subject to . Multiplying both sides by
. Multiplying both sides by 
 (23)
(23)
As before, using theorems 1-6 we obtain
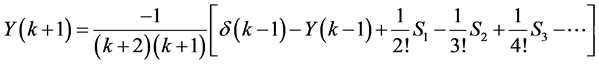 (24)
(24)
where  and
and  are as (18), (19) and (20) respectively for all
are as (18), (19) and (20) respectively for all . Now, from the initial conditions
. Now, from the initial conditions  we have
we have
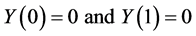 (25)
(25)

Figure 2. Comparison between DTM and Wazwaz’s algorithm.

Table 1. Comparison between DTM and Wazwaz’s algorithm.
Substituting Equation (25) into Equation (24) and by recursive method, the results are listed as follows.
For , we have respectively
, we have respectively

So on, we can use (15) and the closed form of the solution can be easily written as

A solution obtained by Yahya [12] by using the power series method is

We can see Figure 3 and compare with [13] , the results are very good.
As final example and to illustrate the ability of DTM for white-dwarf equation, the next problem is provided for .
.

Figure 3. Numerical results by using DTM.
Example 3 Consider the problem  subject to
subject to . Multiplying both sides by
. Multiplying both sides by 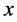 we obtain
we obtain
 (27)
(27)
Here, is easy to verify that the function  has a series expansion
has a series expansion
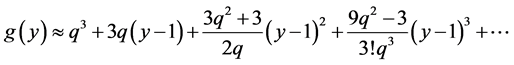 (28)
(28)
where . Therefore, Equation (27) takes the form
. Therefore, Equation (27) takes the form
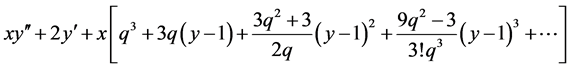 (29)
(29)
Using in (29) the above theorems we have the following
 (30)
(30)
or
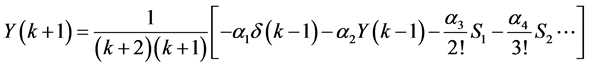 (31)
(31)
where

and successively. Also,
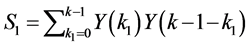 (32)
(32)
 (33)
(33)
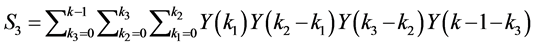 (34)
(34)
for all . Now, from the initial conditions we have
. Now, from the initial conditions we have
 (35)
(35)
Substituting (35) into Equation (31) and by recursive method, the results are listed as follows.
For . or
. or  and then
and then 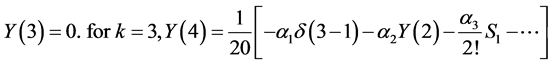 and then
and then . For
. For  and so
and so . For
. For  therefore
therefore . Using (15), the closed form of the soluyion can be easily written as
. Using (15), the closed form of the soluyion can be easily written as

A series solution obtained by Chandrasekhar [2] using series expansion was
 (36)
(36)
Table 2 shows the comparison of  obtained by the DTM and those obtained by Parand [14] . The resulting graph of the white-dwarfs equation in comparison to the present method and the obtained by [14] is show in Figure 4.
obtained by the DTM and those obtained by Parand [14] . The resulting graph of the white-dwarfs equation in comparison to the present method and the obtained by [14] is show in Figure 4.
4. On Convergence of DTM
We can write the DTM as

Table 2 . Comparison between DTM and Legendre-Spectral method.

Figure 4. Comparison between DTM and a Legendre-Spectral Method.
 (37)
(37)
where  increase function depends on its arguments through the function
increase function depends on its arguments through the function . The method (37) means
. The method (37) means  steps, needed for early values
steps, needed for early values  to calculate
to calculate . It is therefore necessary to have bootstrap values
. It is therefore necessary to have bootstrap values .
.
The method (37) is said to be convergent if for all IVP has to

Remark. The condition 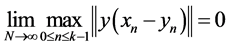 on the bootstrap values is equivalent to asking that
on the bootstrap values is equivalent to asking that  for
for . Here, we are asking that bootstrap values
. Here, we are asking that bootstrap values  approximate well and the initial data
approximate well and the initial data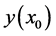 ; if this is not, then no reason to expect that numerical solution closely matches the theoretical.
; if this is not, then no reason to expect that numerical solution closely matches the theoretical.
Now let us consider the following form of the Equation (1)
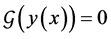 (38)
(38)
Here  is a nonlinear differential operator, which encloses the linear and nonlinear term of the Lane-Emden type equation. Now, the linear term
is a nonlinear differential operator, which encloses the linear and nonlinear term of the Lane-Emden type equation. Now, the linear term  is always invertible and the nonlinear term is
is always invertible and the nonlinear term is  Therefore (38) may be written as
Therefore (38) may be written as
 (39)
(39)
or
 (40)
(40)
Applying DTM in (40) we can obtain
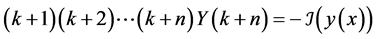 (41)
(41)
Remember that differential transformation of  and
and  are computed by using theorems 1 - 6.
are computed by using theorems 1 - 6.
Let us consider the Equation (38) in the following form
 (42)
(42)
Here,  is a nonlinear operator. It is noted that Equation (15) is equivalent to the sequence
is a nonlinear operator. It is noted that Equation (15) is equivalent to the sequence
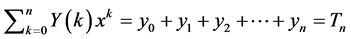 (43)
(43)
This sequence is determined using the iterative scheme
 (44)
(44)
and associated with .
.
The following theorem guarantees that the scheme of DTM converges to the solution 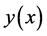 of Lane-Emden Equation (1).
of Lane-Emden Equation (1).
Theorem 7 Let  be a nonlinear operator from a Banach space
be a nonlinear operator from a Banach space  and
and 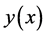 be the solution (exact) of Equation (42). The series solution (14) converges to
be the solution (exact) of Equation (42). The series solution (14) converges to , if there exists a constant
, if there exists a constant  such that
such that  for
for .
.
Proof. We prove that the sequence  is a Cauchy sequence in
is a Cauchy sequence in . Therefore,
. Therefore,

Thus, for any 

so  implying that he sequence
implying that he sequence  is Cauchy, i.e. since
is Cauchy, i.e. since  then
then  , therefore there exists
, therefore there exists  such that
such that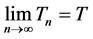 , i.e.
, i.e.  converges.
converges.
Now, we can say too that Equation (42) is similar to solve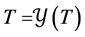 , therefore this implies that if
, therefore this implies that if  is continuous then
is continuous then

i.e. T is a solution of  and this completes the proof.
and this completes the proof.
Figure 5 shows the maximum point-wise error between the numerical solution obtained by using DTM and the Chandrasekhar solution. It is observed that both schemes are almost the same accuracy.

Figure 5. Example 1.  error obtained by using DTM.
error obtained by using DTM.
5. Conclusion
In this work, we presented the definition and handling of one-dimensional differential transformation method. Using DTM, the Lane-Emden equations were transformed into algebraic equations (iterative equations). The new scheme obtained by using DTM yields an analytical solution in the form of a rapidly convergent series. This method makes the solution procedure much more attractive. The figures and tables clearly show the high efficiency of DTM and the convergence of the method for three examples in investigated.
Acknowledgements
Foremost, I would like to express my sincere gratitude to Jean-Christophe Nave (Department of Mathematics and Statics McGill University) for the support of my research and the support of the Department of Mathematics of the Universidad Tecnológica de Pereira (Colombia) and the group GEDNOL.