Ratio-Cum-Product Estimator Using Multiple Auxiliary Attributes in Single Phase Sampling ()
1. Introduction
The use of supplementary information is widely in sampling theory. Auxiliary variables are commonly used in sample survey practices to obtain improved designs and to achieve higher precision in the estimates of some population parameters such as the mean or the total of a study variable. The concept of ratio estimation was introduced in sample survey by Cochran [1] . It is preferred when the study variable is highly positively correlated with the auxiliary variable. Murthy [2] proposed the product estimator for negatively correlated study variable(s) and auxiliary variable which was similar to ratio estimator. Olkin [3] was the first author to use information on more than one supplementary characteristics, which are positively correlated with the variable under study, using a linear combination of ratio estimator based on each auxiliary variable. Raj [4] suggested a method of using multi-auxiliary information in sample survey. Using this idea, Singh [5] proposed a multivariate expression of product estimator where the study variable was negatively correlated with the multi-auxiliary variables. In the same year, Singh [6] proposed a ratio-cum-product estimator and its multi-variable expression. Singh and Tailor [7] proposed a ratio-cum-product estimator for finite population mean in simple random sampling using coefficient of variation and coefficient of kurtosis.
Shabbir and Gupta [8] proposed estimation of the finite population mean with population proportion of an auxiliary variable while Jhajj, Sharma and Grover [9] proposed a general family of estimators using information on auxiliary attribute. They used known information of population proportion possessing an attribute (highly correlated with study variable Y). The attribute is normally used when the auxiliary variables are not available e.g. amount of milk produced and a particular breed of cow or amount of yield of wheat and a particular variety of wheat. Bahland Tuteja [10] proposed ratio and product type exponential estimators using auxiliary attribute. Rajesh, Pankaj, Nirmala and Florentins [11] used the information on auxiliary attribute in ratio estimator in estimating population mean of the variable of interest using known attributes such as coefficient of variation, coefficient of kurtosis and point bi-serial correlation coefficient. Rajesh, S., Pankaj Nirmala and Florentins [11] also used the auxiliary attributes in ratio-product type exponential estimator following the work of Bahland Tuteja [10] . In most of the survey, the auxiliary information is always available and every form of auxiliary information should be used in developing sampling strategies as introduced by Simiuddinand Hanif [12] . We have used those strategies to develop a ratio-cum product estimator using multiple auxiliary attributes in single phase sampling.
Hanif, Haq and Shahbaz [13] proposed a general family of estimators using multiple auxiliary attribute in single and double phase sampling. They also extended their work to ratio, product and regression estimators which were generalization of Naik and Gupta [14] estimator in single and double phase sampling with full information, partial information and no information. The concept of multiple auxiliary attributes was proposed by Hanif, Haq and Shahbaz [15] and [16] , and then extended to ratio and product estimators. In this paper, we have incorporated the multiple auxiliary attributes in Ratio-cum-product estimator proposed by Singh [6] and also incorporate Arora and Bansi [17] approach in writing down the mean squared error.
2. Preliminaries
2.1. Notations
Let  be the
be the  sample point from a population of size N where
sample point from a population of size N where  is the value of variable of interest and
is the value of variable of interest and  =
=  is the value of
is the value of  auxiliary attribute. In defining the attributes we assume complete dichotomy so that;
auxiliary attribute. In defining the attributes we assume complete dichotomy so that;

Let  and
and  be the total number of units in the population and sample respectively possessing attribute
be the total number of units in the population and sample respectively possessing attribute . Let
. Let  and
and  be the corresponding proportion of units possessing a specific attributes
be the corresponding proportion of units possessing a specific attributes  and
and  is the mean of the main variable at first phase.
is the mean of the main variable at first phase.
Further, let ,
,  and
and 
 (1.0)
(1.0)
where  and
and  are sampling errors and are of very small quantities.
are sampling errors and are of very small quantities.
We assume that .
.
Let ,
,  then
then . (1.1)
. (1.1)
Then for simple random sampling without replacement for first phase sampling, we write by using phase wise operation of expectations as:
 ,
,  and
and  (1.2)
(1.2)
where  and
and  are the coefficient of variation of study variable and the auxiliary variables respectively.
are the coefficient of variation of study variable and the auxiliary variables respectively.
The bi-serial correlation coefficient between study variable and auxiliary attributes is given by .
.
If the information proportion  is known for the entire auxiliary attribute, then, a general an estimator is suggested as
is known for the entire auxiliary attribute, then, a general an estimator is suggested as  Where
Where  and
and ,
,  is the sample proportion of
is the sample proportion of  attributes.
attributes.
 is the parametric function such that
is the parametric function such that  and the point
and the point 
are to be bounded set in  containing a point
containing a point 
If A is a square matrix, its inverse can be written using adjoint matrix as,
 (1.3)
(1.3)
 Arora and Lai [17] (1.4)
Arora and Lai [17] (1.4)
The following notations will be used in deriving the mean square errors of proposed estimator.
 Determinant of population correlation matrix of attributes
Determinant of population correlation matrix of attributes 
 Determinant of
Determinant of  minor of
minor of  corresponding to the
corresponding to the  element of
element of 
 Denotes the multiple coefficient of determination of y on
Denotes the multiple coefficient of determination of y on .
.
 Denotes the multiple coefficient of determination of y on
Denotes the multiple coefficient of determination of y on .
.
 Determinant of population correlation matrix of attributes
Determinant of population correlation matrix of attributes .
.
 Determinant of population correlation matrix of attributes
Determinant of population correlation matrix of attributes 
 Determinant of the correlation matrix of
Determinant of the correlation matrix of .
.
 Determinant of the correlation matrix of
Determinant of the correlation matrix of .
.
(1.5)
2.2. Ratio and Product Estimator Using Auxiliary Attribute
The sample mean  using simple random sampling without replacement is given by,
using simple random sampling without replacement is given by,
 (2.1)
(2.1)
while variance of  is given by,
is given by,
 (2.2)
(2.2)
In order to have an estimate of the population mean  the study variable y, assuming the knowledge of the population proportion P, Naik and Gupta [14] defined ratio and product estimators of population mean when the prior information of population proportion of units, possessing the same attribute is variable. Naik and Gupta [14] proposed the following estimators:
the study variable y, assuming the knowledge of the population proportion P, Naik and Gupta [14] defined ratio and product estimators of population mean when the prior information of population proportion of units, possessing the same attribute is variable. Naik and Gupta [14] proposed the following estimators:
 (2.3)
(2.3)
 (2.4)
(2.4)
The MSE of  and
and  up to the first order of approximation are
up to the first order of approximation are
 (2.5)
(2.5)
 (2.6)
(2.6)
The optimums value are  and
and  for ratio and product estimator respectively.
for ratio and product estimator respectively.
2.2. Ratio and Product Estimator Using Multiple Auxiliary Attributes
The ratio and product estimators by Hanif, Haq and Shahbaz [16] for single phase sampling using information on multiple auxiliary attributes are given respectively by,
 (2.7)
(2.7)
 (2.8)
(2.8)
The MSE of the  and
and  up to the first order of approximation are given respectively by,
up to the first order of approximation are given respectively by,
 (2.9)
(2.9)
 (2.10)
(2.10)
3. Methodology
3.1. The Proposed Ratio-Cum-Product Estimator Using Multiple Auxiliary Attributes in Single Phase Sampling
If we estimate a study variable when information on all auxiliary attributes is available from population, it is utilized in the form of their means. By taking the advantage of ratio-cum-product technique for single phase sampling, a generalized estimator for estimating population mean of study variable Y with the use of multi-auxiliary attributes is given by:
 (3.0)
(3.0)
Simplifying (3.0) and substituting (1.0) we get,
 (3.1)
(3.1)
Using (1.0) and (1.1) and ignoring the second and higher terms for each expansion of product and after simplification, we write,
 (3.2)
(3.2)
The mean squared error of ratio-cum-product estimator is given by,
 (3.3)
(3.3)
We differentiate Equation (3.3) partially with respect to  and
and  then equate to zero, using (1.2), (1.3) and (1.4), we get.
then equate to zero, using (1.2), (1.3) and (1.4), we get.
 (3.4)
(3.4)
 (3.5)
(3.5)
Using normal equations that are used to find the optimum values of  and
and  can be written in simplified form as:
can be written in simplified form as:
 (3.6)
(3.6)
Using (1.3) in (3.6), we get,
 (3.7)
(3.7)
Using the optimum value  and
and 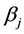 in (3.4), (3.5) in (3.7), we get
in (3.4), (3.5) in (3.7), we get
 (3.8)
(3.8)
Or  (3.9)
(3.9)
Or
 (3.10)
(3.10)
Or
 (3.11)
(3.11)
 (3.12)
(3.12)
3.1. Bias and Consistency of Ratio-Cum-Product Estimators
These ratio-cum-product estimators using multiple auxiliary attribute in single phase sampling is biased. However, these biases are negligible for moderate and large samples. It’s easily shown that the ratio-cumproduct estimator is consistent estimator using multiple auxiliary variables since it is a linear combinations

Table 1. Relative efficiency of existing and proposed estimator with respect to mean per unit estimator for single phase sampling.
of consistent estimators it follows that it is also consistent.
4. Simulation, Results and Discussion
In this section, we carried out some data simulation experiments to compare the performance of ratio-cum product estimator with already existing estimators of finite population mean that uses one or multiple auxiliary attributes. The data for the empirical study is a normally distributed simulated population with the following variables N = 300, n = 45, mean = 45, standard deviation = 5






In order to evaluate the efficiency gain we could achieve by using the proposed estimators, we calculated the variance of mean per unit and the mean squared error of all estimators we considered. We calculated percent relative efficiency of each estimator in relation to variance of mean per unit. We then compared the percent relative efficiency of each estimator, the estimator with the highest percent relative efficiency is considered to be the most efficient compared to other estimators. The efficiency was calculated using the following formulae.
 (4.0)
(4.0)
According to Table 1, the proposed ratio-cum-product estimator using multiple auxiliary attributes in single phase sampling has the highest percent relative efficiency compared to mean per unit, ratio and product estimator using one auxiliary attribute and Ratio and Product estimator using multiple auxiliary attributes in the simulated population. This means that the Ratio-cum-product estimator in single phase sampling is the most efficient estimator compared to the estimators that utilize auxiliary attributes. The proposed ratio-cum-product estimatorusing multiple auxiliary attributesin single phase samplingis recommended to estimate the finite populations mean when all auxiliary attributes are known. In our future work, we will extend this work to two phase sampling.