Proving and Extending Greub-Reinboldt Inequality Using the Two Nonzero Component Lemma ()
1. Introduction
Many authors have established Kantorovich inequality and its generalizations such as Greub-Reinboldt Inequality by variational methods. In a variational approach, one differentiates the functional involved to arrive at an “Euler Equation” and then solves the Euler Equating to obtain the minimizing or maximizing vectors of the functional involved. Solving these Euler Equations is tedious and generally provides little information (see [1] , subsection 4.4 for an example of this method). Others have established Kantorovich-type inequalities for positive operators by going through a two-step process which consists of first computing upper bounds for suitable functions on intervals containing the spectrum of suitable matrix and then applying the standard operational calculus to that matrix (see [2] ) for an example of this method. This method, which we refer to as “the operational calculus method”, has the following two limitations:
First, it does not provide any information about vectors for which the established inequalities become equalities. Second, the operational calculus method is futile in extending Kantorovich-type inequalities to operators on an infinite dimensional Hilbert space. A number of Kantorovich-type inequalities are discussed in [3] .
In this paper we use the author’s Two Nonzero Component Lemma to prove, improve and extend matrix form of Greub-Reinboldt Inequality.
2. The Two Nonzero Component Lemma
In his investigation on problems of antieigenvalue theory the author has discovered a useful lemma which he calls it the Two Nonzero Component Lemma (see [4] -[6] ). Although this Lemma is implicitly used in all of the papers just cited, it was not until 2008 that he stated a formal description of the Lemma in his paper titled, “Antieigenvalue Techniques in Statistics”. Below is the statement of the lemma. For the proof of the lemma please see the author’s work cited above.
Lemma 1 (The Two Nonzero Component Lemma) Let  be the set of all sequences with nonnegative terms in the Banach Space
be the set of all sequences with nonnegative terms in the Banach Space . That is, let
. That is, let
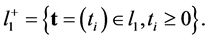 (1)
(1)
Let
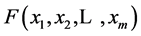 (2)
(2)
be a function from  to
to . Assume
. Assume  for
for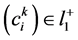 ,
,  , and
, and . Then the minimizing vectors for the function
. Then the minimizing vectors for the function
 (3)
(3)
on the convex set  have at most two nonzero components.
have at most two nonzero components.
What make the proof of the Lemma possible are the following two facts: First, the convexity of the set
 (4)
(4)
Second, a special property that the functions
 (5)
(5)
involved possess. If we set
 (6)
(6)
then all restrictions of the form
 (7)
(7)
of
 (8)
(8)
have the same algebraic form as  itself. For example if
itself. For example if
 (9)
(9)
then we have
 (10)
(10)
which has the same algebraic form as
 (11)
(11)
Indeed, for any ,
,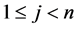 ; all restrictions of the function
; all restrictions of the function
 (12)
(12)
obtained by setting an arbitrary set of 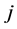 components of
components of  equal to zeros have the same algebraic form as
equal to zeros have the same algebraic form as . Obviously, not all functions have this property. For instance, for the function
. Obviously, not all functions have this property. For instance, for the function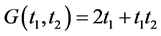 ,
,  , which does not have the same algebraic form as
, which does not have the same algebraic form as .
.
3. Greub-Reinboldt Inequality
Let  and
and  be two real n-tuples. Suppose that
be two real n-tuples. Suppose that ,
,  ,
,  ,
,  are constants such that
are constants such that  and
and . Then, for
. Then, for 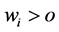 we have
we have
 (13)
(13)
A slightly different form of the above inequality was proved by J. W. S. Cassels in 1951 (see Appendix 1 of [7] ). In the following section we provide a proof for the matrix form of Greub-Reinboldt Inequality based on the Two Nonzero Component Lemma. The proof is completely different than the proofs given by others, including Greub and Reinboldt themselves (see [8] ). This proof has the advantage of providing information about when the inequality becomes equality and gives information about vectors which make the inequality equality. Furthermore, as we will discuss in the Section 5, our method will indeed extend the Greub-Reinboldt Inequality to operators on an infinite dimensional Hilbert space.
4. The Matrix Form of Greub-Reinboldt Inequality
Theorem 2 Let 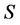 and
and 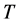 be two commuting positive operators with eigenvalues
be two commuting positive operators with eigenvalues  and
and  respectively. Assume
respectively. Assume
 (14)
(14)
and

Also assume  and
and  are diagonalized with diagonal elements
are diagonalized with diagonal elements  and
and 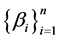 respectively , then
respectively , then
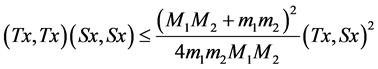 (15)
(15)
for every vector . In this, case if
. In this, case if  is any unit vector which makes the inequality (15) an equality then we have
is any unit vector which makes the inequality (15) an equality then we have
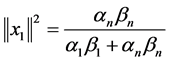 (16)
(16)
and
 (17)
(17)
and
 (18)
(18)
where 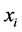 is the projection of
is the projection of 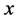 on the eigenspace corresponding to eigenvalue
on the eigenspace corresponding to eigenvalue .
.
Proof. Without loss of generality we can assume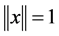 . Consider the functional
. Consider the functional
 (19)
(19)
(19) can be written as
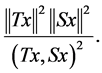 (20)
(20)
The reciprocal of (20) is
 (21)
(21)
The square root of (21) is
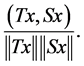 (22)
(22)
To prove (15) we first find
 (23)
(23)
Since  is invertible, by a change of variable we have
is invertible, by a change of variable we have
 (24)
(24)
By the spectral mapping theorem the inf on the right hand side of (24) can be represented as
 (25)
(25)
over the set
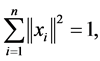 (26)
(26)
where  is the set of eigenvalues of
is the set of eigenvalues of  The fact that
The fact that  and
and  commute implies that
commute implies that
 (27)
(27)
for  and
and
 (28)
(28)
where
 (29)
(29)
and
 (30)
(30)
If we set 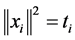 the problem is reduced to finding
the problem is reduced to finding
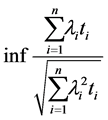 (31)
(31)
over
 (32)
(32)
By the Two Nonzero Component Lemma we need to look at
 (33)
(33)
over the convex set
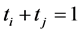 (34)
(34)
for pairs of  and
and 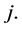 Notice that since the expression in (33) is positive, for simplicity, we can first compute the infimum of the square of that expression on the convex set (34) and then take square root of the result Therefore, the problem is now reduced to finding
Notice that since the expression in (33) is positive, for simplicity, we can first compute the infimum of the square of that expression on the convex set (34) and then take square root of the result Therefore, the problem is now reduced to finding
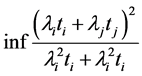 (35)
(35)
on (34). By substituting  in (35) the problem is now reduced to finding
in (35) the problem is now reduced to finding
 (36)
(36)
for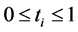 . To find (36), simply differentiate the expression in (36) and set its derivative with respect to
. To find (36), simply differentiate the expression in (36) and set its derivative with respect to 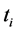 equal to zero (we omit the straight forward computations). The expression in (36) is minimized when
equal to zero (we omit the straight forward computations). The expression in (36) is minimized when

Substituting this value of 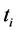 in (34) and the expression in (36) gives us
in (34) and the expression in (36) gives us
 (37)
(37)
and
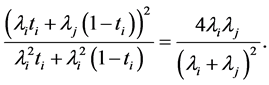 (38)
(38)
Hence
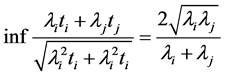 (39)
(39)
and the inf in (39) is attained at
 (40)
(40)
and
 (41)
(41)
Assume that . Now we show that we must have
. Now we show that we must have  and
and . To prove this we must show
. To prove this we must show
 (42)
(42)
for 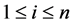 and
and  Squaring both sides of (42) gives us
Squaring both sides of (42) gives us
 (43)
(43)
Thus instead of proving inequality (42) we can prove inequality (43). Let 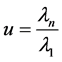 and
and  It is obvious that
It is obvious that
 (44)
(44)
If we substitute 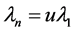 and
and  in (43) we get
in (43) we get
 (45)
(45)
which is equivalent to
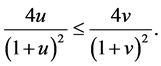 (46)
(46)
Hence proving inequality (42) is reduced to proving inequality (46). To prove (46), note that based on (44)
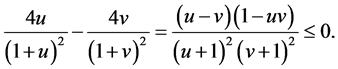 (47)
(47)
Therefore, we must have
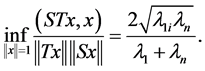 (48)
(48)
The inequality
 (49)
(49)
can be proved the same way we just proved (42). Hence we have
 (50)
(50)
The right side of 50 is simplified to
 (51)
(51)
Thus (50) becomes
 (52)
(52)
Finally (50) is equivalent to
 (53)
(53)
5. Generalizing Greub-Reinboldt Inequality to Operators on a Separable Hilbert Space
There are many proofs for Greub-Reinboldt Inequality in the literature. A significant advantage of proving Greub-Reinboldt Inequality by The Two Nonzero Component Lemma is that we can generalize this inequality to the case of positive operators 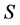 and
and 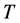 on an separable infinite dimensional separable Hilbert space. This is because, as the statement of the Two Nonzero Component Lemma shows, this lemma is also when the functions
on an separable infinite dimensional separable Hilbert space. This is because, as the statement of the Two Nonzero Component Lemma shows, this lemma is also when the functions  infinite linear combinations of
infinite linear combinations of  Thus we can replace finite summations in (25), (26), (31), (32) with infinite sums and the arguments made in this paper remain valid. However, in this case it seems difficult to the pinpoint the exact pair of
Thus we can replace finite summations in (25), (26), (31), (32) with infinite sums and the arguments made in this paper remain valid. However, in this case it seems difficult to the pinpoint the exact pair of  and
and  for which the projections
for which the projections  and
and  of minimizing unit vectors are nonzero.
of minimizing unit vectors are nonzero.
Theorem 3 Let 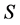 and
and 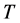 be two commuting positive operators on a separable Hilbert space such that
be two commuting positive operators on a separable Hilbert space such that
 and
and 
 where
where 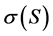 and
and  represent the spectrums of
represent the spectrums of  and
and  respectively, then
respectively, then
 (54)
(54)
for any vector . In this, case if
. In this, case if 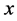 is any unit vector which makes the inequality (54) an equality then there exist a pair of
is any unit vector which makes the inequality (54) an equality then there exist a pair of  and
and  such that
such that
 (55)
(55)
and
 (56)
(56)
and
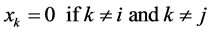 (57)
(57)
where  is the projection of
is the projection of  on the eigenspace corresponding to eigenvalue
on the eigenspace corresponding to eigenvalue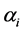 .
.
There are other generalizations of Greub-Reinboldt Inequality. For example in ([9] ) Gustafson extends this inequality to pair noncommuting positive matrices 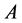 and
and . However, he replaces the standard norm of the Hilbert space with the norm relative to
. However, he replaces the standard norm of the Hilbert space with the norm relative to .
.
Conclusion 4 The Two Nonzero Component Lemma provides an effective way of proving the GreubReinboldt Inequality and extending it to positive operators on separable infinite dimensional Hilbert spaces. The author has also utilized this lemma to prove other Kantorovich-type inequalities. Please see ([4] -[6] [10] [11] ).