Conditions for the Upper Semicontinuous Representability of Preferences with Nontransitive Indifference ()
Keywords
Interval Order, Upper Semicontinuous Numerical Representation, Semiorder

1. Introduction
An interval order  on a set X can be thought of as the simplest model of a binary relation on X whose associated preference-indifference relation is not transitive. Indeed, under certain conditions, it can be fully represented by means of a pair
on a set X can be thought of as the simplest model of a binary relation on X whose associated preference-indifference relation is not transitive. Indeed, under certain conditions, it can be fully represented by means of a pair  of real-valued functions on X, in the sense that
of real-valued functions on X, in the sense that  is equivalent to
is equivalent to  for all
for all . Therefore, interval orders are particularly interesting in economics and social sciences. Whenever the set X is endowed with a topology
. Therefore, interval orders are particularly interesting in economics and social sciences. Whenever the set X is endowed with a topology , it is interesting to look for representations of an interval order
, it is interesting to look for representations of an interval order  on
on  that satisfy suitable continuity conditions.
that satisfy suitable continuity conditions.
The existence of numerical representations of interval orders was first studied by Fishburn [1] [2] and then by other authors (see, e.g., Bosi et al. [3] and Doignon et al. [4] ).
When the set X is endowed with a topology , it may be of interest to look for continuous or at least semicontinuous representations of an interval order
, it may be of interest to look for continuous or at least semicontinuous representations of an interval order  on
on . Results in this direction were presented by Bosi et al. [5] [6] , Chateauneuf [7] and, in the particular case of semiorders, by Candeal et al. [8] [9] .
. Results in this direction were presented by Bosi et al. [5] [6] , Chateauneuf [7] and, in the particular case of semiorders, by Candeal et al. [8] [9] .
For many purposes, the existence of a representation  with u and v both upper semicontinuous is satisfactory. In particular, if such a representation exists and the topology
with u and v both upper semicontinuous is satisfactory. In particular, if such a representation exists and the topology  is compact, then there exist maximal elements for the interval order
is compact, then there exist maximal elements for the interval order  which are obtained by maximizing u or v. Also the existence of undominated maximal elements can be guaranteed by means of an approach of this kind (see, e.g., Alcantud et al. [10] ). This kind of semicontinuous representability of interval orders was first studied by Bridges [11] and then by Bosi and Zuanon [12] [13] .
which are obtained by maximizing u or v. Also the existence of undominated maximal elements can be guaranteed by means of an approach of this kind (see, e.g., Alcantud et al. [10] ). This kind of semicontinuous representability of interval orders was first studied by Bridges [11] and then by Bosi and Zuanon [12] [13] .
In this paper, we present different results concerning the representability of an interval order  on a topological space
on a topological space 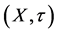 by means of a pair
by means of a pair  of upper semicontinuous real-valued functions.
of upper semicontinuous real-valued functions.
2. Notations and Preliminaries
An interval order  on a set X is an irreflexive binary relation on X which in addition satisfies the following condition for all
on a set X is an irreflexive binary relation on X which in addition satisfies the following condition for all :
:

An interval order  is in particular a partial order (i.e.,
is in particular a partial order (i.e.,  is an irreflexive and transitive binary relation). The preference-indifference relation
is an irreflexive and transitive binary relation). The preference-indifference relation  associated to an interval order
associated to an interval order  on set X is defined as follows for all
on set X is defined as follows for all :
:

It is well know that if  is an interval order, then
is an interval order, then  is total (i.e., for all
is total (i.e., for all , either
, either  or
or ). On the other hand,
). On the other hand,  is not transitive in general.
is not transitive in general.
Fishburn [2] proved that if  is an interval order on a set X, then the following two binary relations
is an interval order on a set X, then the following two binary relations  and
and  (the traces of the original interval order) are weak orders (i.e., asymmetric and negatively transitive binary relations on X):
(the traces of the original interval order) are weak orders (i.e., asymmetric and negatively transitive binary relations on X):


The following proposition was proved, for example, by Alcantud et al. ([10] , Lemma 3).
Proposition 2.1. Let  be an irreflexive binary relation on a set X. Then
be an irreflexive binary relation on a set X. Then  is an interval order if and only if
is an interval order if and only if  is a asymmetric.
is a asymmetric.
An interval order  on a set X is a weak order if and only if
on a set X is a weak order if and only if . The preference-indifference relations
. The preference-indifference relations  and
and  associated to the binary relations
associated to the binary relations  and
and  are defined as follows for all
are defined as follows for all :
:

Therefore, we have that


An interval order  on a set X is said to be i.o. separable (see Bosi et al. [3] and Doignon et al. [4] ) if there exists a countable subset D of X such that for all
on a set X is said to be i.o. separable (see Bosi et al. [3] and Doignon et al. [4] ) if there exists a countable subset D of X such that for all  with
with  there exists
there exists  such that
such that . In this case D is said to be an i.o. order dense subset of
. In this case D is said to be an i.o. order dense subset of .
.
From Chateauneuf [7] , an interval order  on a set X is said to be strongly separable if there exists a countable set
on a set X is said to be strongly separable if there exists a countable set  such that, for every
such that, for every  with
with , there exist
, there exist  with
with . D is said to be a strongly order dense subset of X. It is clear that strong separability implies i.o. separability. Further, strong separability occurs, for example, whenever an interval order is representable by means of a pair
. D is said to be a strongly order dense subset of X. It is clear that strong separability implies i.o. separability. Further, strong separability occurs, for example, whenever an interval order is representable by means of a pair  of nonnegative positively homogeneous functions on a cone in a topological vector space. This kind of representability, in the more general setting of acyclic binary relations, was studied, for example, by Alcantud et al. [14] and in the case of not necessarily total preorders by Bosi et al. [15] .
of nonnegative positively homogeneous functions on a cone in a topological vector space. This kind of representability, in the more general setting of acyclic binary relations, was studied, for example, by Alcantud et al. [14] and in the case of not necessarily total preorders by Bosi et al. [15] .
If R is a binary relation on a set X, then denote by  and
and  the lower section and respectively the upper section of any element
the lower section and respectively the upper section of any element , i.e., for every
, i.e., for every ,
,

A subset A of a related set  is said to be R-decreasing if
is said to be R-decreasing if  for every
for every .
.
A real-valued function u on X is said to be a weak utility function for a partial order  on a set X if, for all
on a set X if, for all ,
,

The following characterization of the existence of an upper semicontinuous weak utility for a partial order on a topological space is well known (see e.g. Alcantud and Rodríguez-Palmero ([16] , Theorem 2)).
Proposition 2.2. Let  be a partial order on a topological space
be a partial order on a topological space . Then the following conditions are equivalent:
. Then the following conditions are equivalent:
1) There exists an upper semicontinuous weak utility function u for ;
;
2) There exists a countable family  of open
of open  -decreasing subsets of X such that if
-decreasing subsets of X such that if  then there exists
then there exists  such that
such that ,
, .
.
A real-valued function u on X is said to be a utility function for a partial order  on a set X if, for all
on a set X if, for all ,
,

If a partial order  admits a representation by means of a utility function, then
admits a representation by means of a utility function, then  is a weak order or equivalently the associated preference-indifference relation
is a weak order or equivalently the associated preference-indifference relation  is a total preorder (i.e.
is a total preorder (i.e. 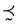 is total and transitive).
is total and transitive).
The following proposition is well known and easy to be proved.
Proposition 2.3. Let  be a weak order on a topological space
be a weak order on a topological space . Then the following conditions are equivalent:
. Then the following conditions are equivalent:
1) There exists an upper semicontinuous utility function u for ;
;
2) There exists a countable family  of open
of open -decreasing subsets of X such that if
-decreasing subsets of X such that if  then there exists
then there exists  such that
such that ,
, .
.
A pair  of real-valued functions on X represents an interval order
of real-valued functions on X represents an interval order  on X if, for all
on X if, for all ,
,

If  is a representation of an interval order
is a representation of an interval order , then it is easily seen that u and v are weak utility functions for
, then it is easily seen that u and v are weak utility functions for  and
and , respectively, while it is not in general guaranteed that u and v are utility functions for
, respectively, while it is not in general guaranteed that u and v are utility functions for 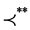 and
and , respectively.
, respectively.
We say that a pair  of real-valued functions on X almost represents an interval order
of real-valued functions on X almost represents an interval order  on X if, for all
on X if, for all ,
,

An interval order  on a topological space
on a topological space  is said to be upper (lower) semicontinuous if
is said to be upper (lower) semicontinuous if

is an open subset of X for every . If
. If  is both upper and lower semicontinuous, then it is said to be continuous.
is both upper and lower semicontinuous, then it is said to be continuous.
If there exists a representation  of an interval order
of an interval order  on a topological space
on a topological space  and u and v are both upper semicontinuous, then
and u and v are both upper semicontinuous, then  is necessarily upper semicontinous, due to the fact that
is necessarily upper semicontinous, due to the fact that

is open for every . In this case, also the associated weak order
. In this case, also the associated weak order  is upper semicontinuous, since
is upper semicontinuous, since

is expressed as union of open sets.
On the other hand, the existence of an upper semicontinuous representation does not imply that the weak order  is upper semicontinuous. The following example, that was already presented in Bosi and Zuanon [13] , illustrates this fact.
is upper semicontinuous. The following example, that was already presented in Bosi and Zuanon [13] , illustrates this fact.
Example 2.4. Let X be the set  endowed with the natural induced topology on the real line and consider the interval order
endowed with the natural induced topology on the real line and consider the interval order 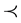 on X defined as follows for all
on X defined as follows for all :
:

If we define  and
and  for every
for every , then it is clear that
, then it is clear that 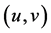 is an (upper semi) continuous representation of
is an (upper semi) continuous representation of . We can easily verify that the associated weak order
. We can easily verify that the associated weak order  is not upper semicontinuous. Indeed, consider for example that
is not upper semicontinuous. Indeed, consider for example that  is not an open set. Notice that
is not an open set. Notice that  for all
for all ,
,  since
since  but for no
but for no  we have that
we have that  because this would imply the existence of
because this would imply the existence of  such that
such that .
.
A weak order  on a topological space
on a topological space  is said to be weakly upper semicontinuous if for every
is said to be weakly upper semicontinuous if for every  that is not a minimal element there exists a uniquely determined
that is not a minimal element there exists a uniquely determined  -decreasing open subset
-decreasing open subset  of X such that
of X such that  and
and  (see Bosi and Zuanon [13] ). This definition was presented by Bosi and Herden [17] in the context of preorders (i.e., reflexive and transitive binary relations). If a weak order
(see Bosi and Zuanon [13] ). This definition was presented by Bosi and Herden [17] in the context of preorders (i.e., reflexive and transitive binary relations). If a weak order  on a topological space
on a topological space  admits an upper semicontinuous weak utility u then it is weakly upper semicontinuous (just define, for every
admits an upper semicontinuous weak utility u then it is weakly upper semicontinuous (just define, for every ,
,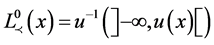 ). Further, it is clear that an upper semicontinuous weak order is also weakly upper semicontinuous.
). Further, it is clear that an upper semicontinuous weak order is also weakly upper semicontinuous.
If  is a topological space and S is a dense subset of
is a topological space and S is a dense subset of  such that
such that , then we say that a family
, then we say that a family 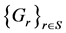 of open subsets of X is a quasi scale in
of open subsets of X is a quasi scale in  if the following conditions hold:
if the following conditions hold:
1) ;
;
2)  for every
for every  such that
such that .
.
The following proposition is a particular case of Theorem 4.1 in Burgess and Fitzpatrick [18] .
Proposition 2.5. If  is a quasi scale in a topological space
is a quasi scale in a topological space , then the formula
, then the formula

defines an upper semicontinuous function on  with values in
with values in .
.
3. Conditions for the Semicontinous Representability of Interval Orders
In the following theorem we present some conditions that are equivalent to the existence of an upper semicontinuous representation of an interval order on a topological space.
Theorem 3.1. Let  be an interval order on a topological space
be an interval order on a topological space . Then the following conditions are equivalent:
. Then the following conditions are equivalent:
1) There exists a pair  of upper semicontinuous real-valued functions on
of upper semicontinuous real-valued functions on  representing the interval order
representing the interval order ;
;
2) The following conditions are verified:
a) The interval order  on X is representable by means of a pair of real-valued functions
on X is representable by means of a pair of real-valued functions ;
;
b)  is upper semicontinuous;
is upper semicontinuous;
c) There exists an upper semicontinuous weak utility  for
for ;
;
3) The following conditions are verified:
a) The interval order  on X is i.o.-separable;
on X is i.o.-separable;
b)  is upper semicontinuous;
is upper semicontinuous;
c) There exists a countable family 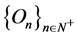 of open
of open  -decreasing subsets of X such that if
-decreasing subsets of X such that if  then there exists
then there exists  such that
such that ,
, ;
;
4) There exists a countable family  of pairs of upper semicontinuous real-valued functions on
of pairs of upper semicontinuous real-valued functions on
 almost representing
almost representing  such that for every
such that for every  with
with  there exists
there exists  with
with  .
.
5) There exists a countable family  of pairs of open subsets of X satisfying the following conditions:
of pairs of open subsets of X satisfying the following conditions:
a)  and
and  imply
imply  for all
for all  and for all
and for all ;
;
b)  and
and  imply
imply  for all
for all  and for all
and for all ;
;
c) for all  such that
such that  there exists
there exists  such that
such that ,
, ;
;
6) There exist two quasi scales  and
and  in
in  such that the family
such that the family  satisfies the following conditions:
satisfies the following conditions:
a)  and
and  imply
imply  for every
for every  and
and ;
;
b) for every  such that
such that  there exist
there exist  such that
such that ,
, 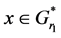 ,
, .
.
Proof. The equivalence 1) Û 5) was proved in Bosi and Zuanon ([12] , Theorem 3.1), while the equivalences 1) Û 2) and 1) Û 3) were proved in Bosi and Zuanon ([13] , Theorem 3.1).
Let us prove the equivalence of conditions 1) and 4). It is clear that 1) implies 4). In order to show that 4) implies 1), assume that there exists a countable family  of pairs of upper semicontinuous real-valued functions on
of pairs of upper semicontinuous real-valued functions on  almost representing
almost representing  such that for every
such that for every  with
with  there exists
there exists  with
with . Without loss of generality, assume that
. Without loss of generality, assume that  and
and  take values in
take values in  for every index n. Define functions u and v on X as follows:
for every index n. Define functions u and v on X as follows:

in order to immediately verify that  is an upper semicontinuous representation of the interval order
is an upper semicontinuous representation of the interval order  on the topological space
on the topological space .
.
Finally, let us show that also the equivalence of conditions 1) and 6) is valid. In order to show that 1) implies 6), assume without loss of generality that there exists a pair of upper semicontinuous real-valued functions with values in  representing the interval order
representing the interval order  on the topological space
on the topological space . Then just define
. Then just define 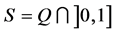 ,
,  ,
,  for every
for every , and
, and  in order to immediately verify that
in order to immediately verify that  and
and  are two quasi scales in
are two quasi scales in  such that the family
such that the family  satisfies the above subconditions a) and b) of condition 6).
satisfies the above subconditions a) and b) of condition 6).
In order to show that 6) implies 1), assume that there exist two quasi scales  and
and  such that the family
such that the family  satisfies the above subconditions a) and b) in condition 6). Then define two functions
satisfies the above subconditions a) and b) in condition 6). Then define two functions
 as follows:
as follows:


We claim that  is a pair of continuous functions on
is a pair of continuous functions on  with values in
with values in  representing the interval order
representing the interval order .
.
From the definition of the functions u and v, it is clear that they both take values in . Let us first show that the pair
. Let us first show that the pair  represents the interval order
represents the interval order . First consider any two elements
. First consider any two elements  such that
such that . Then, by condition b), there exist
. Then, by condition b), there exist  such that
such that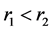 ,
,  ,
, . Hence, we have
. Hence, we have  , which obviously implies that
, which obviously implies that . Conversely, consider any two elements
. Conversely, consider any two elements  such that
such that , and observe that, for every
, and observe that, for every , if
, if  then it must be
then it must be  by the above condition a). Hence, it must be
by the above condition a). Hence, it must be  from the definition of u and v.
from the definition of u and v.
Finally, observe that u and v are upper semicontinuous real-valued functions on  with values in
with values in 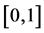 as an immediate consequence of Proposition 2.5. This consideration completes the proof. QED It has been noticed that if
as an immediate consequence of Proposition 2.5. This consideration completes the proof. QED It has been noticed that if  is a representation of an interval order
is a representation of an interval order  on a set X, then not necessarily u is a utility function for the trace
on a set X, then not necessarily u is a utility function for the trace . The following immediate corollary to Theorem 3.1 concerns this particular case.
. The following immediate corollary to Theorem 3.1 concerns this particular case.
Corollary 3.2. Let  be an interval order on a topological space
be an interval order on a topological space . Then the following conditions are equivalent:
. Then the following conditions are equivalent:
1) There exists a pair  of upper semicontinuous real-valued functions on
of upper semicontinuous real-valued functions on  representing the interval order
representing the interval order 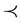 such that u is a utility function for the associated weak order
such that u is a utility function for the associated weak order ;
;
2) The following conditions are verified:
a) The interval order  on X is representable by means of a pair of real-valued functions
on X is representable by means of a pair of real-valued functions ;
;
b)  is upper semicontinuous;
is upper semicontinuous;
c)  is upper semicontinuous;
is upper semicontinuous;
3) The following conditions are verified:
a) The interval order  on X is i.o.-separable;
on X is i.o.-separable;
b)  is upper semicontinuous;
is upper semicontinuous;
c) There exists a countable family 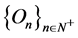 of open
of open  -decreasing subsets of X such that if
-decreasing subsets of X such that if  then there exists
then there exists  such that
such that ,
, .
.
Since Bridges ([11] , Proposition 2.3) proved that an interval order  on a second countable topological space
on a second countable topological space  is representable by a pair
is representable by a pair  of (nonnegative) real-valued function, we have that the following corollary is an immediate consequence of the previous theorem.
of (nonnegative) real-valued function, we have that the following corollary is an immediate consequence of the previous theorem.
Corollary 3.3. Let  be an interval order on a second countable topological space
be an interval order on a second countable topological space . Then the following conditions are equivalent:
. Then the following conditions are equivalent:
1) There exists a pair  of upper semicontinuous real-valued functions on
of upper semicontinuous real-valued functions on  representing the interval order
representing the interval order ;
;
2) The following conditions are verified:
a) 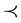 is upper semicontinuous;
is upper semicontinuous;
b) There exists an upper semicontinuous weak utility  for
for .
.
The following corollary is a consequence of both Corollary 3.2 and Corollary 3.3.
Corollary 3.4. Let  be an interval order on a second countable topological space
be an interval order on a second countable topological space . Then the following conditions are equivalent:
. Then the following conditions are equivalent:
1) There exists a pair  of upper semicontinuous real-valued functions on
of upper semicontinuous real-valued functions on 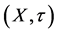 representing the interval order
representing the interval order  such that u is a utility function for the associated weak order
such that u is a utility function for the associated weak order ;
;
2) The following conditions are verified:
a)  is upper semicontinuous;
is upper semicontinuous;
b)  is upper semicontinuous.
is upper semicontinuous.
The following corollary is found in Bosi and Zuanon ([13] , Proposition 3.1).
Corollary 3.5. Let  be a strongly separable interval order on a topological space
be a strongly separable interval order on a topological space . Then the following conditions are equivalent:
. Then the following conditions are equivalent:
1) There exists a pair  of upper semicontinuous real-valued functions on
of upper semicontinuous real-valued functions on  representing the interval order
representing the interval order ;
;
2) The following conditions are verified:
a)  is upper semicontinuous;
is upper semicontinuous;
b)  is weakly upper semicontinuous.
is weakly upper semicontinuous.
We finish this paper by presenting some applications of the previous results to the semiorder case. We recall that a semiorder  on an arbitrary nonempty set X is a binary relation on X which is an interval order and in addition verifies the following condition for all
on an arbitrary nonempty set X is a binary relation on X which is an interval order and in addition verifies the following condition for all :
:

If  is a semiorder, then the binary relation
is a semiorder, then the binary relation  is a weak order (see e.g. Fishburn [2] ). The following proposition was proved by Bosi and Isler ([19] , Proposition 3).
is a weak order (see e.g. Fishburn [2] ). The following proposition was proved by Bosi and Isler ([19] , Proposition 3).
Proposition 3.6. Let  be an interval order on a set X. Then
be an interval order on a set X. Then  is a semiorder if and only if
is a semiorder if and only if  is asymmetric.
is asymmetric.
Clearly, this happens in the particular case when . More generally, we have that the following proposition holds. The easy proof of it is left to the reader.
. More generally, we have that the following proposition holds. The easy proof of it is left to the reader.
Proposition 3.7. Let  be an interval order on a set X. If there is a real-valued function u on X that is a weak utility for both
be an interval order on a set X. If there is a real-valued function u on X that is a weak utility for both  and
and , then
, then  is semiorder.
is semiorder.
Since it was already observed that upper semicontinuity of an interval order  always implies upper semicontinuity of the associated weak order
always implies upper semicontinuity of the associated weak order , we obtain the following corollaries as other immediate consequences of Theorem 3.1.
, we obtain the following corollaries as other immediate consequences of Theorem 3.1.
Corollary 3.8. Let  be a semiorder on a topological space
be a semiorder on a topological space . If
. If  is upper semicontinuous and
is upper semicontinuous and , then there exists a pair
, then there exists a pair  of upper semicontinuous real-valued functions on
of upper semicontinuous real-valued functions on  representing
representing  provided that there exists a pair
provided that there exists a pair  of real-valued functions on X representing
of real-valued functions on X representing .
.
Corollary 3.9. Let  be a semiorder on a second countable topological space
be a semiorder on a second countable topological space . If
. If 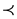 is upper semicontinuous and
is upper semicontinuous and , then there exists a pair
, then there exists a pair  of upper semicontinuous real-valued functions on
of upper semicontinuous real-valued functions on  representing
representing .
.