Hydrodynamic Flow between Two Non-Coincident Rotating Disks Embedded in Porous Media ()
1. Introduction
Hydrodynamic viscous incompressible fluid flow through a porous medium have been attracted the attention of number of researchers due to its wide applications in engineering and geophysical applications, viz. in the petroleum technology to study the movement of natural gas, oil and water through the oil reservoirs, in chemical engineering for filtration and purification process, in agriculture engineering to study the underground water resources. The viscous incompressible fluid flow due to non-coaxial rotations of a disk and a fluid at infinity has been studied by a number of researchers. The flow of a viscous incompressible fluid confined between two parallel plates rotating with the same angular velocity about non-coincident axes has been studied by Berker [1] and Abbott and Walters [2]. Erdogan [3,4] have studied the flow due to parallel disks rotating about non-coincident axes with one of the disk or both the disks oscillating in its own plane. The fluid flow between eccentric rotating disks under different environment has been studied by Ersoy [5-7]. The flow of a viscoelastic fluid between rotating disks has been studied by Rajagopal [8]. The hydromagnetic flow between two rotating disks with noncoincident parallel axes of rotation has been studied by Mohanty [9]. Kanch and Jana [10] have investigated the Hall effects on hydromagnetic flow between two rotating disk with non-coincident parallel axes of rotation. Guria et al. [11] have studied the unsteady MHD flow between two disks with non-coincident parallel axes of rotation. Maji et al. [12] have studied the effect of rotation on unsteady MHD flow between disks, rotating with same angular velocity about two different axes. Guria et al. [13] have studied the magnetohydrodynamic flow with reference to non-coaxial rotation of a porous disk and a fluid at infinity. Effects of Hall current on unsteady MHD flow between disks with non-coincident parallel axes of rotation have been studied by Das et al. [14].
In this paper, we have studied the combined effects of rotation and porosity on the hydrodynamic flow between two disks rotating with same angular velocity about two different axes at a distant a apart. In the light of our present problem it is rigorously stated that there arises symmetric motion about the mid plane between the two disks as referred to a rigid body rotation.
2. Formulation of the Problem and Its Solution
Let us consider the steady flow of a viscous incompressible fluid between two parallel disks, embedded in a porous medium, rotating with uniform angular velocity  about two different axes at a distance a apart. We choose a system of cylindrical polar co-ordinates
about two different axes at a distance a apart. We choose a system of cylindrical polar co-ordinates  with the axis normal to the disks as situated symmetrically between two axes of rotation. The axis of rotation of the disk
with the axis normal to the disks as situated symmetrically between two axes of rotation. The axis of rotation of the disk  lies to the right and that of the disk
lies to the right and that of the disk 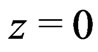 lies to the left of the z-axis [see Figure 1].
lies to the left of the z-axis [see Figure 1].
The Navier-Stokes equation of motion is
 (1)
(1)
where q, p,  ,
,  and
and  are, respectively, the velocity vector, the fluid pressure, the density of the fluid, the fluid viscosity and the permeability of the porous medium.
are, respectively, the velocity vector, the fluid pressure, the density of the fluid, the fluid viscosity and the permeability of the porous medium.
The equation of continuity is
 (2)
(2)
The boundary conditions of the problem are
 (3)
(3)
Subject to the above boundary conditions, we assume the velocity components as
 (4)
(4)
On the use of (4), we have from Equation (1)
 (5)
(5)
 (6)
(6)
 (7)
(7)
where prime refers to differentiation with respect to z. It is interesting to note that Equations (5)-(7) do not contain any non-linear terms in  and
and .
.
Eliminating p from Equations (5)-(7), we obtain
 (8)
(8)
 (9)
(9)
which imply
 (10)
(10)
 (11)
(11)
The boundary conditions (3) become
 (12)
(12)
Equations (5) and (6) can be written in a dimensionless form as
 (13)
(13)
 (14)
(14)
where
 (15)
(15)
Integrating the above Equations (13) and (14) with respect to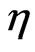 , we get
, we get
 (16)
(16)
 (17)
(17)
where  and
and  are unknown constants.
are unknown constants.
The corresponding boundary conditions (12) become
 (18)
(18)
Combining Equations (16) and (17), we have
 (19)
(19)
where
 and
and . (20)
. (20)
The boundary conditions (18) reduce to
 (21)
(21)
In the case of a symmetric flow, we may choose the constant  and the Equation (19) becomes
and the Equation (19) becomes
 (22)
(22)
The solution of the Equation (22) subject to the boundary conditions (21) can be obtained in the following form
 (23)
(23)
where
 (24)
(24)
Using (20) with the separating of real and imaginary parts, we have
 (25)
(25)
 (26)
(26)
If , i.e. in the absence of a porosity of the medium, the above equations reduce to
, i.e. in the absence of a porosity of the medium, the above equations reduce to
 (27)
(27)
 (28)
(28)
which are identical with Equations (21) and (22) as the result obtained by Abbott and Walters[10].
3. Results and Discussions
To study the effects of rotation and porosity on the flow between two disks embedded in porous medium with non-coincident parallel axes of rotation, the dimensionless primary velocity f and secondary velocity g are depicted graphically against  for various values of rotation parameter
for various values of rotation parameter  and porosity parameter
and porosity parameter  in Figures 2-3. Figure 2 demonstrates that the velocities f and g increase with an increase in
in Figures 2-3. Figure 2 demonstrates that the velocities f and g increase with an increase in  to the left of the z-axis while to the right of the z-axis they decrease with
to the left of the z-axis while to the right of the z-axis they decrease with

Figure 2. Variations of primary velocity f and secondary velocity g for σ = 0.2.

Figure 3. Variations of primary velocity f and secondary velocity g for K2 = 5.
increase in . Figure 3 shows that the primary velocity f decreases with an increase in
. Figure 3 shows that the primary velocity f decreases with an increase in  to left of the z-axis while it increases with an increase in
to left of the z-axis while it increases with an increase in  to the right of the z-axis. On the other hand, the secondary velocity g increases with an increase in
to the right of the z-axis. On the other hand, the secondary velocity g increases with an increase in  to the left of the z-axis while it becomes reversed to right of the z-axis.
to the left of the z-axis while it becomes reversed to right of the z-axis.
The non-dimensional shear stresses due to the primary and the secondary flows at the disks  and
and  are given by
are given by
 (29)
(29)
 (30)
(30)
The torque exerted by the fluid to overcome the transverse shearing stress on a disk of radius b, such as
 (31)
(31)
The values of the torque  at the disks are shown in Figure 4 for different values of
at the disks are shown in Figure 4 for different values of  against
against . It is seen from Figure 4 that the torque (
. It is seen from Figure 4 that the torque ( ) on the disks increases with an increase in either
) on the disks increases with an increase in either  or
or .
.
We shall discuss some special cases of interest:
Case 1: When  and
and . In this case, we have from Equation (23), on separating into a real and imaginary parts
. In this case, we have from Equation (23), on separating into a real and imaginary parts
 (32)
(32)
 (33)
(33)
It is seen from the Equation (32) that the effects of rotation parameter 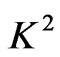 on the velocity distribution
on the velocity distribution  is important only when we consider the order of
is important only when we consider the order of .
.
Case 2: For large rotation of the disks i.e. for  and
and , we get from Equation (23) on separating into a real and imaginary parts.
, we get from Equation (23) on separating into a real and imaginary parts.
 (34)
(34)
 (35)
(35)
where
 (36)
(36)
The Equations (34) and (35) show the existence of the single-deck boundary layer of thickness of the order , where
, where  is given by (36). This boundary layer thickness decreases with an increase in either rotation parameter
is given by (36). This boundary layer thickness decreases with an increase in either rotation parameter  or porosity parameter
or porosity parameter , since
, since  increases with an increase in either
increases with an increase in either  or
or .
.
Case 3: When  and
and . In this case, we have from Equation (23), on separating into a real and imaginary parts
. In this case, we have from Equation (23), on separating into a real and imaginary parts
 (37)
(37)
 (38)
(38)
Equation (37) demonstrates the existence of the single-deck boundary layer of thickness of the order . This boundary layer thickness increases with an increase in porosity parameter
. This boundary layer thickness increases with an increase in porosity parameter . It is interesting to note that for small value of
. It is interesting to note that for small value of , the boundary layer thickness is independent of rotation parameter
, the boundary layer thickness is independent of rotation parameter . Further, for small values of
. Further, for small values of , the secondary velocity vanishes in the azimuthal direction.
, the secondary velocity vanishes in the azimuthal direction.
Case 4: Single rotating disk
In the limit , that is, when the disk at
, that is, when the disk at  is placed at an infinite distance, then the solution (23) yields, on using (20)
is placed at an infinite distance, then the solution (23) yields, on using (20)
 (39)
(39)
 (40)
(40)
where
 (41)
(41)
The Equations (39) and (40) show that there exist a thin boundary layer near the disk . The thickness of this boundary layer is of order
. The thickness of this boundary layer is of order  where
where 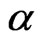 is given by (41). This boundary layer thickness increases with an increase in
is given by (41). This boundary layer thickness increases with an increase in , since
, since  decreases with an increase in
decreases with an increase in . It is interesting to note that in the limit as
. It is interesting to note that in the limit as , we arrived the result of the hydrodynamic viscous flow due to non-coincident rotations of a disk and a fluid at infinity embedded in porous medium.
, we arrived the result of the hydrodynamic viscous flow due to non-coincident rotations of a disk and a fluid at infinity embedded in porous medium.
4. Conclusions
Hydrodynamic viscous incompressible fluid flow between two non-coincident rotating disks embedded in porous media is studied. An exact solution of the governing equations has been obtained in a closed form. It is found that the primary velocity f decreases and the secondary velocity g increases with increase in porosity parameter to the left of the z-axis and the result is reversed to the right of the z-axis. It is also found that the torque on the disks increases with increase in either rotation parameter or porosity parameter. In the limit of , we derived the result of hydrodynamic flow of a viscous fluid due to non-coaxial rotations of a disk and a fluid at infinity embedded in a porous medium.
, we derived the result of hydrodynamic flow of a viscous fluid due to non-coaxial rotations of a disk and a fluid at infinity embedded in a porous medium.