Nonlinear Dynamic Characteristics of a Simple Blade with Breathing Crack Using Ansys Software ()
1. Introduction
A crack, one of the most common defects in a structure, may result in a dangerous effect on the dynamic behavior of structures. It may lead to improper structural performance, which can eventually destroy the structure. Generally, a crack induces changes in the structure's stiffness, and also reduces the frequency of the structure. The vibration of cracked structures has attracted considerable interest from many researchers due to its practical importance and the numerous issues that arise in the context of linear and nonlinear dynamics theories. The dynamic characteristics of a cracked structure and an intact structure are different in principle. The reason for this difference is the change in stiffness when a structure is cracked. During vibration, a crack will open and close in time due to an externally applied loading. This phenomenon is known as the breathing process of the crack. A fatigue crack or breathing crack can occur in rotating blade or turbine blade. During the breathing process the two edges of the crack surface come into and out of contact, thus the stiffness in the crack region may increase or decrease. This will cause changes in dynamic response of the cracked element which would be useful for detection of cracks [1]. The presence of a crack in a structural member introduces a local flexibility that affects its dynamic response. Moreover, the crack will open and close in time depending on the loading conditions and vibration amplitude. The local flexibility of a crack has been widely used in the past 15 years for vibration analysis. It is well known that damages reduce the stiffness of a mechanical system. A crack in a structural element causes variations in its stiffness that can affect the dynamics of the whole structure. It results in the reduction in natural frequencies and changes in mode shapes of vibration. Many authors have investigated in different ways the relationship between the crack characteristics, localization and depth, and the vibration properties of the mechanical element [2].
In the early stages of this area of study, most investigations used an assumption that the cracks of the structures are always open, and thus contact between the crack surfaces does not occur. It is convenient to assume that the crack is always open because the system remains linear. However, this assumption is not accurate in many cases. For example, for structures with fatigue-induced cracks, the gaps between the crack surfaces are very small, and the closing of the crack surfaces occurs in reality [3]. Furthermore, if the cracked structure is a rotating machinery component, such as a blade disk in a turbine engine rotor, then considering the effects of rotation on the nonlinear vibration response is important. An extensive literature survey regarding research activities on rotating beams was provided by [4]. It should be noted that the change in the rotating equilibrium configuration due to the inertial loading is of particular interest for the vibration analysis of cracked structures. The initial gap between the crack surfaces can change significantly with increasing rotation speed. Some structures, such as turbine blades, propellers, satellites, etc., rotate while in operation and the rotating speeds are constant for many applications. The dynamic characteristics of rotating elastic bodies are different from their dynamic characteristics in the nonrotating state. The difference is come from the centrifugal force which causes to change in the stiffness of the body by an amount which is called the “apparent stiffness” by Hurty and Rubinstein in 1964 or called sometimes “geometric stiffness” described by Likins in 1974 as mentioned in the paper published by [5].
For the study of cracked Bernoulli–Euler beams, a pioneering contribution was made by [6] in their application of the Hu–Washizu–Barr variational principle to the cracked beam problem. Further extension was made by [7] for Bernoulli–Euler beams with symmetric cracks and single-edge cracks [8]. A generalization to the theory was made by [9]. However, in these studies, the nonlinear effect was not considered. Reference [10] pointed out that measured natural frequencies of a beam with a fatigue crack differ from those calculated without considering the crack closing effect. He also addressed the significance of the crack closing effect for accurately predicting the frequency shifts due to cracking. Reference [11] considered the vibration response of a beam with breathing crack. A cantilever beam was used and modeled as a one-degree-of-freedom lumped parameter system. This simplified model simulates the beam vibrating at its first mode. They incorporated the breathing crack model into a single-degree-of-freedom system as a harmonic change in the beam stiffness. Their analysis showed that the natural frequency reduction for a fatigue crack (breathing crack) was much smaller than that for an open crack.
Reference [12] simulated a breathing crack state in a single degree of freedom of T-beam using piece wise linear time record based on bilinear stiffness model. From their results, they explained. The general consensus in their literature is that the natural frequencies for the closed crack state should be higher than those from open and breathing crack states and the frequencies for the breathing crack state should lie between those for the closed and open crack states. They indicated that there was substantial inconsistent variation across the modes, especially for non-flexural mode. Reference [13] investigated the effect of a crack due to the rotating speed of a composite beam by applying Timoshenko beam theory. The finite element method is used to model and numerically analyzed the crack. The researchers reported that natural frequency of the breathing crack model was greater than the open crack model while the amplitude of vibration was reduced. Reference [14] used continuous cracked beam vibration theory is used for the prediction of changes in transverse vibration of a simply supported beam with a single edge breathing crack. The eigen-frequency changes due to a breathing edge-crack are shown to depend on the bi-linear character of the system. They showed that using an open-crack model assumption to interpret vibration measurements for a fatigue-breathing crack will lead to the incorrect conclusion that the crack severity is smaller than what it really is. Reference [15] developed a tester based on the resonant frequency method. That tester measures contact stiffness. The contact load was varied from 100 to 1000 mili Newton. Both Hertzian and flat surfaces were tested under unlubricated dry conditions, and in the presence of minute amounts of lubricant and wear debris. In typical tests, the system resonance was assumed constant independent of the load, whereas the contact resonant frequency was shift with increasing contact load. The measured contact stiffness for both Hertzian and flat rough surfaces was favorably compared with modeled predictions. Reference [16] stated that the nonlinearity due to the crack closing effect has to be considered for the in-plane bending case but crack closing was neglected in their study because their work focused on the out-of-plane bending vibration. Reference [17] simulated a dynamic model for cracked blade on periodically varying load. They concluded that the assumption of linear (open) crack is not real and he showed that there was a distinct difference in amplitudes for linear and nonlinear cracked blades. They showed in the results that the amplitude response in method of remotely nonlinear response is greater that linear response.
One of the most important goals in the present search is to better understanding why the difference between the results for same breathing modeling. To accomplish this, an experimental and theoretical investigation to the nonlinear behaviors of a cracked structure is proposed. Effects of rotation with breathing phenomenon together were also investigated. A finite element method is used to analyze the nonlinear vibration of a rotating blade with a crack. In particular, the solution of the forced vibration of a cracked rotor blade made from Ti-6Al-4V is investigated. The breathing effect of the crack, the effects of rotation, and crack ratio are considered in this study.
2. Finite Element Discretization
The finite element method is the most powerful numerical technique, which offers an approximate solution to most realistic types of structures. The use of the computational tools becomes common in design, and the need for explicit design formulas have therefore decreased. More direct and accurate calculations may be performed in order to achieve safe and optimal design. Here, ANSYS is used to analyze the rotor blade.
2.1. Element Parameters
SOLID187 element is a higher order 3-D, 10-node element is used to mesh the blade. SOLID187 has a quadratic displacement behavior and is well suited to modeling irregular meshes. TARGE170 is used to represent various 3-D “target” surfaces for the associated contact elements. CONTA174 is used to represent contact and sliding between 3-D “target” surfaces (TARGE170) and a deformable surface, defined by this element. The element is applicable to 3-D structural and coupled field contact analyses. This element is located on the surfaces of 3-D solid or shell elements with mid side nodes (SOLID187). It has the same geometric characteristics as the solid or shell element face with which it is connected. Contact occurs when the element surface penetrates one of the target segment elements (TARGE170) on a specified target surface. The coordinate system for these elements are shown in Figure 1.
2.2. Blade Geometry and Mesh Generation
The blade is discretized using solid element (solid187). ANSYS finite element program was used as a mathematical tool in the analysis of this model. Figure 2 shows the finite element representation of the blade structure. It must be noted that, the number of the elements in the crack location must be sufficient to give the required accuracy and controlling the dramatic changes that occurs at the crack location. Therefore, some convergence studies should be induced to obtain the required numbers of element for covering the mesh processes. After these studies, it was noted that the element number should be not less than 6350 elements for the blade geometry.
All dimensions of the blade are listed in Table 1 below.

Table 1. Dimensions of the proposed blade model.

Figure 2. Blade configuration and mesh generation.
2.3. Strain Displacement Relation
The strain-displacement relationship can be written with its dependence explicitly expressed as, [18].
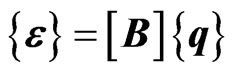 (1)
(1)
where  is Strain vector,
is Strain vector,  is strain-displacement matrix and
is strain-displacement matrix and 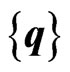 is the Nodal displacement vector.
is the Nodal displacement vector.
All elements of strain-displacement matrix are derived in terms of the shape function derivatives and the Jacobian matrix.
2.4. Element Stiffness and Mass Matrices
In general, the basic concept of the finite elements method is to discrete the continuum into a definite numbers of small elements connected together at their common nodes. Depending on the strain-displacement matrix,  , the element stiffness
, the element stiffness  and element mass
and element mass  matrices can be written as; [18],
matrices can be written as; [18],
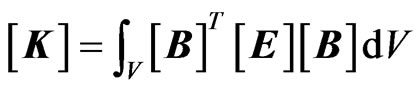 (2)
(2)
 (3)
(3)
where  is stress-strain matrix,
is stress-strain matrix,  is the shape function matrix, V is the volume and ρ is the mass density.
is the shape function matrix, V is the volume and ρ is the mass density.
2.5. Dynamic Governing Equilibrium Equation
In this paper, the vibration of a rotor blade composed of linear isotropic elastic material is considered. In this study, nonlinearities other than the one due to intermittent contact at the crack surfaces are not considered. The symbols b(t) and f(q) are the time dependent external force and the nonlinear force respectively. Thus, the governing equation of the cracked blade is [19]
 (4)
(4)
2.6. Contact Stiffness
A stiffness relationship between two bodies must be established for contact to occur. Without a contact stiffness, bodies will pass through one another. The relationship is generated through an elastic spring that is put between the two bodies, where the contact force is equal to the product of the contact stiffness (kc) and the penetration (δ). The amount of penetration (δ), or incompatibility, between the two bodies is therefore dependent on the stiffness kc. Ideally, there should be no penetration, but this implies that kc = infinity, which will lead to numerical instabilities. The value of kc that is used depends on the relative stiffness of the bodies in contact. The contact stiffness is determined by the following relationships [20]:
 (5)
(5)
where Km is the bulk modulus of contacted element, A0 is the area of contact segments, V0 is the volume between contacted segments and fs is the penalty factor.
3. Experiment Test Validation
In this study, the experimental data are used to verify the proper use of ANSYS software. A simple beam model is used to perform a numerical validation by comparing the results of transient finite element analysis (FEA) with contact elements to those from experiment test. Thus, a simple model, such as a cracked cantilever beam, is used. First, it is important to estimate the mechanical properties of the tested beam. The universal test machine (UTM) is used to find the elastic modulus of the beam material. After several tests, the average elastic modulus is found to be about 204 GPa with 7840 kg/m3 mass density. Finally, the beam is tested dynamically by using vibration data collector TVC200D apparatus to find its natural frequency as depicted in Figure 3.
The presence of a crack in the beam, according to the principle of Saint-Venant, causes a perturbation of the stress field in the neighborhood of the breach. Such a perturbation is relevant especially when the crack is open and determines a local reduction of the flexural rigidity. On the other hand, when the crack is closed the beam acts, approximately, as a homogeneous beam with no crack [21]. Three cases of cantilevered beam is tested namely a beam without crack, a beam with open crack, and a beam with breathing crack. Table 2 lists the beam geometry and crack dimensions. While, Table 3 lists the given experimental data and the corresponding ANSYS results.


Figure 3. Tested data and vibration kit.

Table 2. Dimensions of tested beam.

Table 3. Experiment versus finite element results.
As can be seen, the nonlinear systems have higher resonant frequencies than the linear systems and breathing frequency lies between the uncracked (or closed crack) and opened crack natural frequencies. This indicates that the compliance of the linear system is greater than that for the nonlinear systems, which makes sense because penetration of the crack surfaces is allowed for the linear case.
4. Results and Discussion
Table 4 lists the mode shapes and corresponding crack ratios. The modes of interest being third, fourth, fifth, and sixth because these modes represent the in plane and out plane deformed shapes of the structure.
It is very clear that the presence of the crack has a great effect on the modes of deformation as shown in Figure 4. The increasing of crack ratio (crack length/ blade width) from 0 to 0.2 exhibits no effect on the mode shape but an increasing in the amplitude of the deformation will occur. At a crack ratio of 0.4, an exchange in the mode shapes occurs, so that the 5th mode will veering to the 4th mode and then transform from sin bending mode to in plane one (breathing crack).
In other words, the 4th mode is transferred to the 5th one at 0.4 crack ratio which means a reduction in the overall stiffness due to the increasing the crack ratio. The transformation between modes means that there is a reduction or lack in the stiffness (local stiffness) that in turn leads to change in the overall stiffness. These transformations between modes, due to the changes in crack ratios, give an excellent imagination that what the crack can do. The changing in several modes and no changing in the others for a specific crack ratio means that there is a critical crack length just at which the mode interactions phenomenon are occurred [3].
4.1. Effect of Crack Ratio on Time and Frequency Domains
In the time domain, the amplitude history with time was showed. The more important is to obtain the eigen modes for both linear and nonlinear crack models. Therefore, the frequency domain is constructed using FFT (Fast Fourier Transform). The comparison of the frequency domain is fulfilled between linear and nonlinear cracked models.
If one creates a FE model with a crack and performs forced response analysis or modal analysis without considering the crack-closing effect, then the response is linear (penalty stiffness is not existed on the crack surfaces). This modeling approach does not preserve cyclic symmetry in the geometry of the tuned system, but it does yield a linear system. This approach is referred to linear cracked blade model. The nonlinear cracked blade model is the cracked blade model where the intermittent contact of the crack surfaces during the vibration is fully considered.
The frequency domain gives a good explanation about the frequency at maximum response amplitude. Figure 5 presents the time responses for linear (open crack, no contact) and nonlinear (breathing crack, with contact) vibrations, the breathing effect is very clear when its compared with linear mode.
In the other hand, the displacement of nonlinear response in the negative direction (the direction that leads to converge the crack surfaces) is smaller than open crack displacement. This is a good indication about the effect of penalty stiffness (compression spring element) which resulted from crack surface impact. To distinct the eigen frequency, Figure 6 is conducted in frequency

Figure 4. Modes veering and transformation.

Table 4. Present crack ratios and corresponding mode shapes.

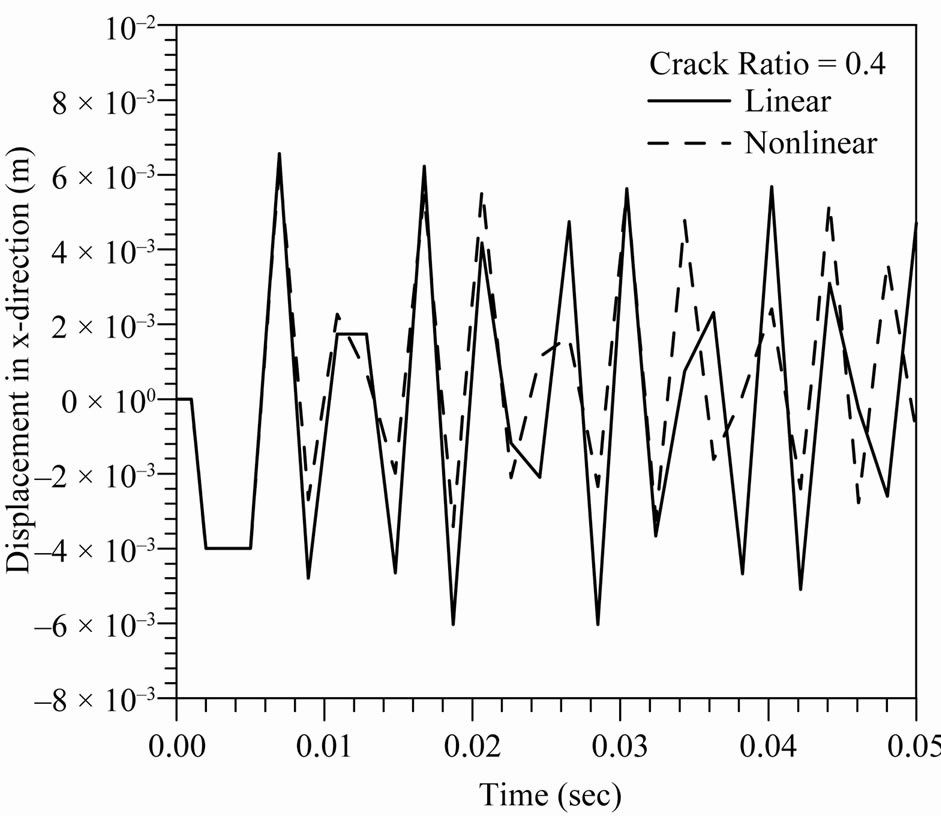
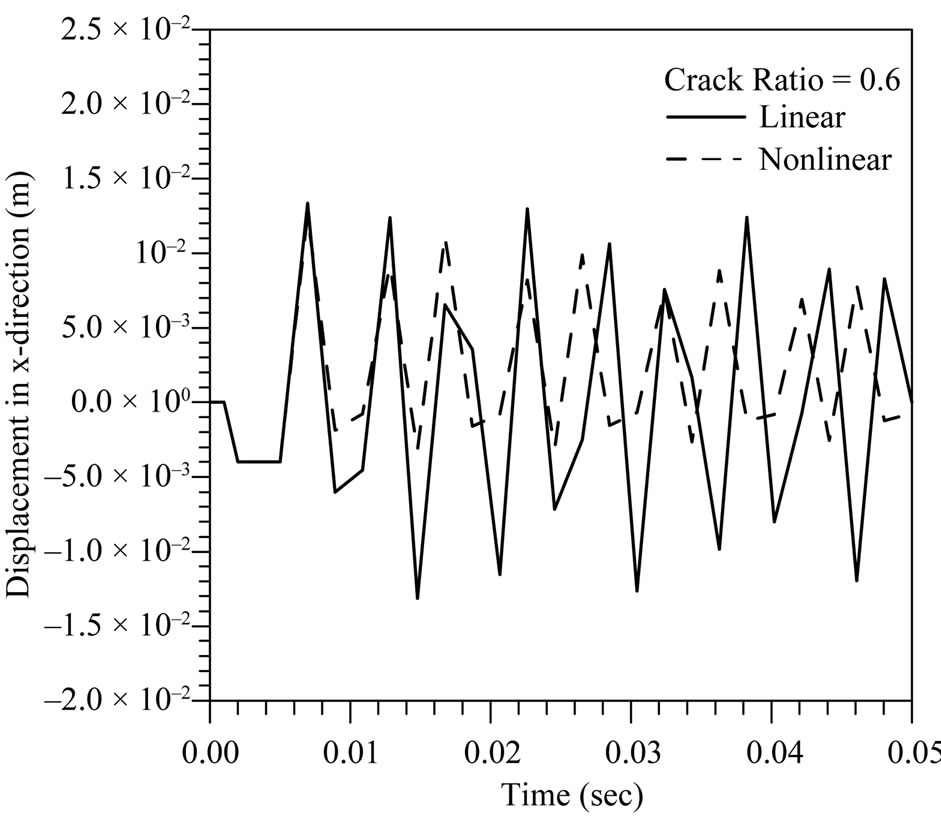
Figure 5. Tip end displacement with time of cracked blade with different crack ratios.



Figure 6. Frequency response for linear and nonlinear cracked blade with different crack ratios.
domain. As can be seen, the frequency response function predicted by the linear cracked blade does not match that predicted by the nonlinear cracked blade model.
The most notable distinction between the results from the linear model and the nonlinear model is that the resonant frequencies of the cracked-blade dominated response shifts significantly toward higher frequencies for the nonlinear case. This effect is due to the intermittent contact at crack surfaces, the so-called closing or breathing crack effect. Namely, the stiffness of the cracked blade is underestimated by the linear model that neglect contact and so are the resonant frequencies.
Generally, the distinctions between linear and nonlinear frequencies and amplitudes are increased with the increasing the crack ratio due to the combined effects of mass and stiffness of the cracked structure (reduction in the stiffness because of the mass discontinuity).
4.2. Effect of Rotating Velocity and Crack Ratio
The effect of rotating velocity on the natural frequencies of the blade is shown in Figure 7. It is obvious that the blade natural frequencies are increased with increasing the rotor velocity for all selected modes. This event is caused by increasing the centrifugal force that in turn leads to increase the stress stiffening (spinning stiffness). It should be pointed that the increasing frequency bandwidth is different from mode to another. There are little changes in the blade frequencies for the in-plane bending modes (5, 5, 4 and 4 for crack ratios 0, 0.2, 0.4, and 0.6 respectively) when they compared with other modes. The main reason for this little change is that the rotating velocity provides a centrifugal force leads by the way to create a reversed moment load tends to re-back the blade to its equilibrium shape. However, the blade deformation
at resonant frequency for the in-plane mode is smaller than other bending modes. Thus, the rotational velocity has no significant effects on the blade dynamic characteristics.
It is important to clear that a reversed moment is the product of multiplying the centrifugal force by the instantaneous distance between the deformed center at resonant frequency and the equilibrium blade mass center. The other bending modes (4, 4, 5 and 5 for crack ratios 0, 0.2, 0.4 and 0.6 respectively) seem to be the most affected one, because these modes having out of plane nature at the resonant frequencies (sin wave) and the centrifugal force produces a reversed moment.
5. Conclusions
The following conclusions can be deduced from this study as:
1) The presence of the crack in the structure does not change all modes shapes but there are critical crack lengths for each mode lead to interchanging between them.
2) The increasing in the natural frequency with the increasing in the angular velocity in the presence of the crack means that the effect of the crack is decreased with increasing the velocity.
3) Increasing crack ratio lead to increase the structure time response, i.e. increasing nonlinearity.
4) Breathing crack natural frequency lies between open crack and closed crack natural frequencies of that structure.
5) The presence of the mode interchanging and mode crossover is a guide on the nonlinear response for the cracked structure.