Characterization of Self Dual Lattices in R, R₂ and R₃

Comlan de Souza, David W. Kammler

Department of Mathematics, California State University at Fresno, Fresno, USA.
Department of Mathematics, Southern Illinois University at Carbondale, Carbondale, USA.

DOI: 10.4236/am.2014.510137                

Abstract

This paper shows that the only self dual lattices in R, R², R³  are rotations of Z , Z×Z and Z×Z×Z.

Keywords

Self Dual Lattice

1. Introduction

Let

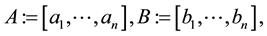
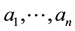be nonsingular real matrices with column vectors and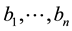, respectively. Let

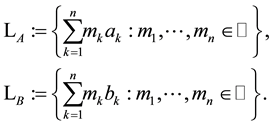
be the lattices in that are generated by the columns of. The lattice will be a subset of the lattice 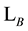if and only if the generators of all lie in, i.e.,

for suitably chosen integers. Equivalently,

i.e.,

is a matrix of integers. Analogously, the lattice is a subset of if is a matrix of integers. In this way we see that

if and only if both and

are matrices with integer elements. When this is the case, and are both integers and since

this implies that

Such a matrix is said to be unimodular. The above analysis (that can be found in [1] ) is summarized as follows.

Theorem 1 The lattices are identical if and only if

is a matrix of integers with

Corollary 1 Lattices are preserved under integer column operations.

Proof 1 Let generate the lattice, and let

be a strictly upper triangular matrix of integers. Then is an upper triangular matrix of integers with a unit diagonal, and we can write

where

is a strictly upper triangular matrix of integers. The columns of

i.e.,

generate the same lattice as the columns of A. To see this we observe that

is a matrix of integers with unit determinant.

2. Dual lattices

Definition 1 Two linearly independent sets of real (column) vectors and are said to be biorthogonal if

where is the Kronecker’s delta, denotes the transpose and denotes the usual inner product. When the columns of

and

are biorthogonal, we find

so that

This being the case, given linearly independent vectors we can form and then obtain the biorthogonal vectors as the columns of

The lattice generated by vectors biorthogonal to is said to be the dual of the lattice. More generally, is dual to if and only if generates the same lattice as, i.e.,

is a matrix of integers with determinant.

Suppose now that generate the same lattice, i.e.,

Let

be the generators of lattices dual to, respectively. Since

we see that will be a matrix of integers with determinant if and only if the same is true of. Thus if and only if.

We are interested in characterizing those lattices that are self dual, i.e.,

This will be the case if and only if

is a matrix of integers with determinant. Since

this will be the case only if

or equivalently

In this way we see that a lattice is self dual if and only if is a matrix of integers with unit determinant. The parallelopiped in with vertices, i.e., the unit cell of the lattice has the volume

[2] [3] . Thus a lattice can be self dual only if each of its primitive cells, has unit volume.

Self dual lattices are preserved under orthogonal transformations. Indeed, let be an orthogonal transformation on, i.e.,

and let be the lattices generated by the columns of a nonsingular matrix and. The matrix

has columns

that generate the lattice. We can use such a matrix to rotate, to reflect one or more vectors of the set, to permute, etc. The lattice which is dual to is generated by the columns of

i.e., by

Thus the generators of the dual lattice are transformed in the same way as the generators of the lattice. In this way we see that a lattice is self dual if and only if the lattice is self dual. Indeed,

so is a matrix of integers with unit determinant if and only if the same is true of. Moreover, since

we see that the orthogonal transformation preserves the Euclidean lengths of a set of generators for the lattice.

3. Main results

We will now show that the only self dual lattices in are rotations of, and, respectively.

The case n = 1

Let be a vector in that generates the lattice. We do not change the lattice if we assume that

. Let be biorthogonal to. The lattice generated by will be identical to the

lattice if and only if

i.e., if and only if

Thus the only self dual lattice in is the lattice

The case n = 2

Theorem 2 Every self dual lattice in is some rotation of.

Proof 2 Let where are linearly independent vectors in and assume that is self dual. Fix the origin at some lattice point of and rotate the axes, if necessary, so that the nearest nonzero lattice point of lies on the positive -axis, i.e.

where and

(1.1)

The lattice does not change if is replaced by so we can and do assume that. Likewise the lattice does not change if is replaced by since this is the result of an integer column operation. Thus we can and do assume that

(1.2)

By hypothesis the lattice is self dual so the same is true of. This implies that

and

Since is self dual, the first column of can be expressed as an integral linear combination of the columns of, i.e.,

where. In this way we see in turn that

(1.3)

for some

(1.4)

for some and

(1.5)

Using these expressions with (1.2) we find

so

Using these expressions with (1.1) we find

and since

this implies that

It follows that and. In this way we prove that, i.e., the columns of and thus those of are orthonormal. Thus is some rotation of.

A theorem of Minkowski [1] states that

where is the shortest nonzero vector in a lattice in. Within the present context, this leads to the bound

which implies that Our argument gives from which we immediatly obtain.

Another result in [4] states that if is a self-dual lattice in then

which leads to

The case n = 3

Theorem 3 Every self dual lattice in is some rotation of.

Proof 3 Let the self dual lattice in be generated by the columns of chosen so that are as small as possible subject to the constraint

Following the analysis from the previous section, we set

where is an orthogonal matrix chosen so that

with

By hypothesis the lattice is self dual, and since is orthogonal, the same is true of. This being the case

Since the lengths of the generators of the lattice are preserved under the orthogonal transformation, it follows that

(1.6)

The columns of (and thus the columns of) have been chosen to be as small as possible subject to the above constraints, so we must have

(1.7)

It can be verified that has the inverse

and after using to simplify the components we obtain

Since is self dual, the columns of generate the same lattice as the columns of so we can write

and

for suitably chosen In this way we see in turn that

(1.8)

(1.9)

for some and

(1.10)

We also have

(1.11)

(1.12)

for some and

so that

(1.13)

Using (1.7) and (1.8)-(1.12) we find

(1.14)

Using (1.6) and (1.7) we see that,

which implies that

Again using (1.6) and (1.7) we see that,

which implies that

so that

Since we must have

or

In this way we see in turn that and so that Finally, we again use (1.6) with (1.13), (1.12), (1.9) to write

It follows that so we must have and In this way we see that the columns of ( and thus those of) must be orthonormal. Thus is some rotation of.

Suppose now that are linearly independent vectors in and that

where. We know that

where the biorthogonal vectors are the columns of. In this way we see that

if and only if is self dual, where. This proves the following.

Theorem 4 Let be linearly independent vectors in. Then

if and only if

for some orthonormal choice of the vectors.

Analogously, we can prove the following 3-dimensional generalization.

Theorem 5 Let be linearly independent vectors in. Then

if and only if

for some orthonormal choice of the vectors.

These results correspond to the familiar identity

III ^˄= III

from univariate Fourier analysis. The possibility of rotations (other than reflections) in slightly complicates the generalization of this result.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Kannan, R. (1987) Minkowski’s Convex Body Theorem and Integer Programming. Mathematics of Operations Research, 12, 415-440.
[2]	Strang, G. (1976) Linear Algebra and Its Applications. Academic Press, Inc., New York.
[3]	Senechal, M. (1995) Quasicrystals and Geometry. Cambridge University Press, New York.
[4]	Conway, J.H., Odlyzko, A.M. and Sloane, N.J.A. (1978) Extremal Self-Dual Lattices Exit Only in Dimensions 1 to 8, 12, 14, 15, 23, and 24.